牙本质区域对塑性损伤力学性能的影响研究

李兴国，申 同，侯鹏斐，金 宽，陈云龙

(太原科技大学 应用科学学院，太原 030024)

牙本质是牙齿的主要组成部分，对于人的咀嚼等日常活动有着重要作用。由于牙本质有着特殊的微观结构，其力学性能随着牙本质的深度发生变化。这也是为什么老年人的牙齿显得透明的缘故。因此研究牙本质力学性能随着牙本质深度的变化对于临床治疗具有重要的意义。

由于牙本质微观结构非常复杂以及可制作试样尺寸很小，采用传统的测试方法很难表征其梯度力学性质，因此大量的研究采用压痕法测量牙本质及牙釉质的力学性能[1-3]。徐远志等[4]采用纳米压痕法测量了人牙本质的硬度和弹性模量，发现牙本质的硬度和弹性模量与压痕点与牙髓腔的距离有很强的相关性。此外牙冠部牙本质在釉牙本质界面附近硬度和弹性模量会减小[5]。

牙本质的非线性力学性能如塑性及损伤性能也非常重要，采用传统的实验的方法很难测量。而采用数值模拟可以很方便的研究牙本质的塑性及损伤性能。An等[6]的采用数值模拟的方法研究了牙釉质的力学性能，发现牙釉质的塑性性能和弹性性能一样具有明显的梯度力学性质。然而该方法采用理想弹塑性模型不能很好的拟合卸载曲线的最后阶段。这是由于未考虑到压痕载荷作用下的压痕点附近材料发生损伤的情况[7]。然而关于牙本质的塑性和损伤力学性能是否也和牙釉质类似具有梯度力学性质，尚未见诸报道。

本文通过数值模拟研究牙本质距离牙髓腔不同区域的塑性及损伤力学性质，探讨这种影响对牙齿功能的影响。本文建立了在牙本质纳米压痕作用下的塑性损伤模型，研究牙本质的塑性力学性能和损伤力学性能，阐述牙本质所在区域对牙本质力学性质的影响。

1 数值模型

1.1 模型的建立

采用压痕法测试时，压痕点附近的材料应力非常复杂，因此很难获得相应的材料的力学参数。本文采用数值模拟的方法模拟牙本质的纳米压痕测试来研究牙本质的非线性力学性能。采用纳米压痕测试牙本质力学性能时，其加载曲线和的卸载曲线不重合，表明牙本质发生了塑性变形。此外卸载的最后阶段，牙本质的刚度显著低于卸载的初始阶段。由此可证明牙本质发生了损伤。本文通过建立塑性损伤的数值模型，研究纳米压痕实验过程中牙本质的塑性及损伤力学性能。由于牙本质和皮质骨材料都是由矿物质和蛋白质组成，具有相似的微观结构，而皮质骨是一种典型的粘聚-摩擦材料，采用Drucker-Prager屈服模型可以很好的描述其屈服行为。本文采用双曲型的Drucker-Prager屈服函数f来描述牙本质的塑性变形。

(1)

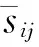
α=(σb0/σc0-1)/(2σb0/σc0-1)

(2)

β=

(3)

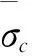
牙本质的本构关系可以表示为：

(4)

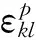
Cijkl=Mδijδkl+G(δikδjl+δilδjk)

(5)

其中M和G是Lame常数，δij为Kronecker delta符号。塑性应变率通过流动法则来确定：

(6)

(7)

塑性势f为:

(8)

其中φ是膨胀角。

图1为本模型在受到单轴压缩时的应力应变曲线示意图，由图可知，材料在屈服之后发生损伤。

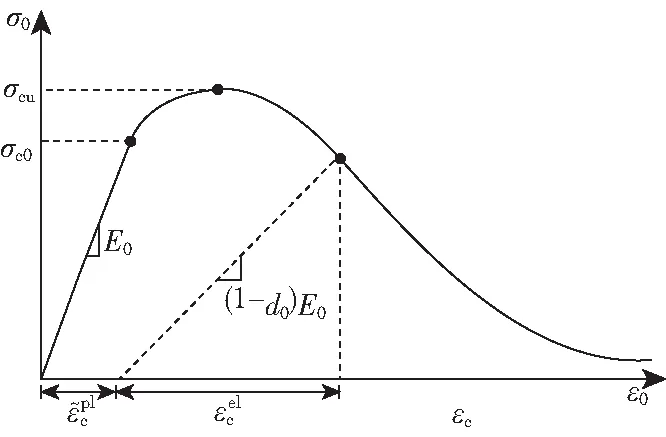
图1 塑性损伤模型的在单轴压缩作用下的应力应变曲线示意图

在本数值模型中，牙本质弹性模量由纳米压痕实验得到；其屈服强度通过数值模拟拟合实验所测量得到的载荷与压入深度曲线得到，先前的研究表明这种拟合方法在确定生物材料力学性质时非常有效。本模型中，牙本质的弹性模量和屈服强度如表1所示。其他参数选取v=0.3；σb0/σc0=1.125，φ=15°.由于在纳米压痕加载过程中材料发生的损伤主要由压应力引起，本文中牙本质的损伤由压力引起的等效塑性应变来表征。牙本质损伤D为：

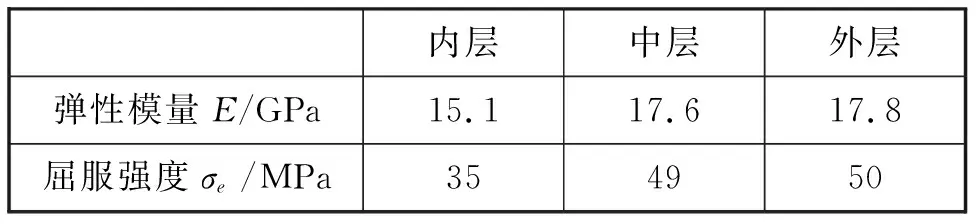
表1 数值模型参数[4]

D=p(1-e-qεp)

(9)

参数p和q通过数值计算拟合实验测得的载荷与压入深度曲线得到。本模型中分别为0.9和5.

1.2 有限元分析

在本数值模型中，纳米压痕测试时的Berkovich压头简化为半顶角70.3°的圆锥压头，由于实验过程中压头变形极小，为简化计算设置压头为刚体[6-7]。并假定牙本质与压头无摩擦接触[8-9]。由于简化后压头为圆锥形具有轴对称性，结合实验的加载过程可将模型简化为轴对称模型。牙本质材料模型选择塑性损伤模型，加载方式与纳米压痕实验过程相同选择力加载方式。分别模拟三个区域的牙本质的纳米压痕测试。在本模型中，采用24 764个四节点双线性轴对称单元(CAX4R，ABAQUS 6.10-1)对牙本质进行离散，离散网格如图2所示。

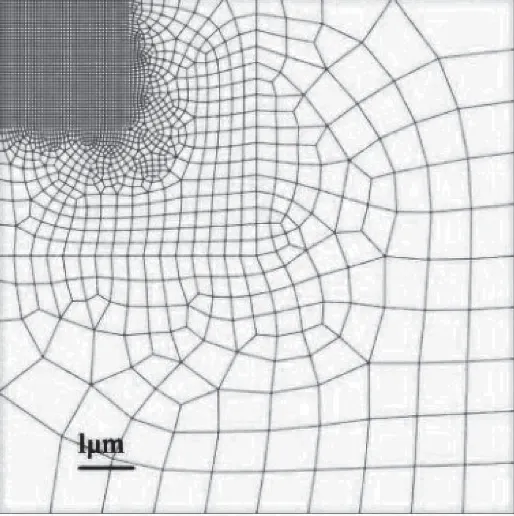
图2 有限元模型

2 结果

本文建立的牙本质塑性损伤数值模型所得的数值结果与实验吻合得很好。图3是数值模拟和实验对比的结果。由图3可知，采用塑性损伤模型不仅可以描述了卸载阶段与加载阶段曲线不重合现象，并且材料在卸载阶段刚度出现下降也能很好的体现出来。说明塑性损伤模型可以很好的描述压痕作用下牙本质的力学行为。

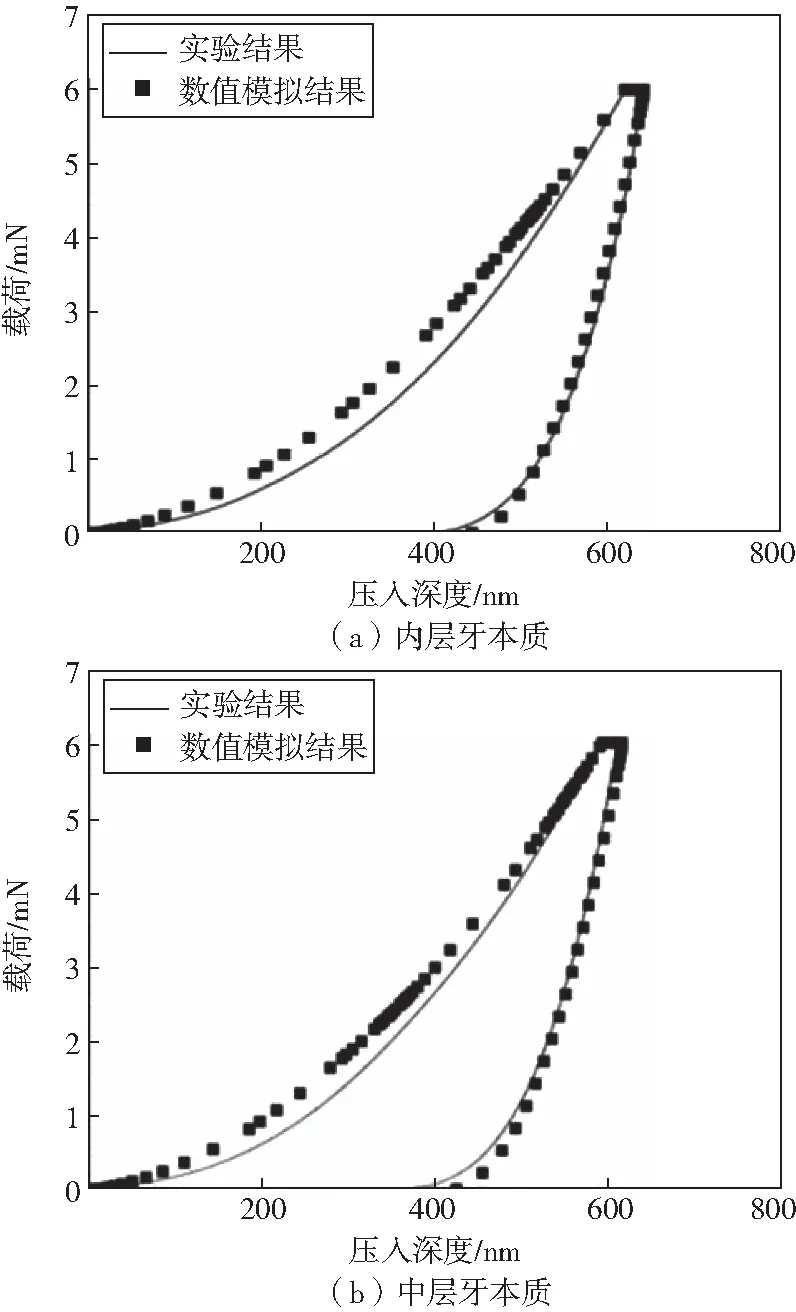
图3 牙本质的纳米压痕实验曲线与数值模拟结果

由数值模拟得到牙本质从内层到外层的屈服强度分别为35 MPa、49 MPa和50 MPa.结果表明内层牙本质的屈服强度低于中层和外层牙本质的屈服强度。

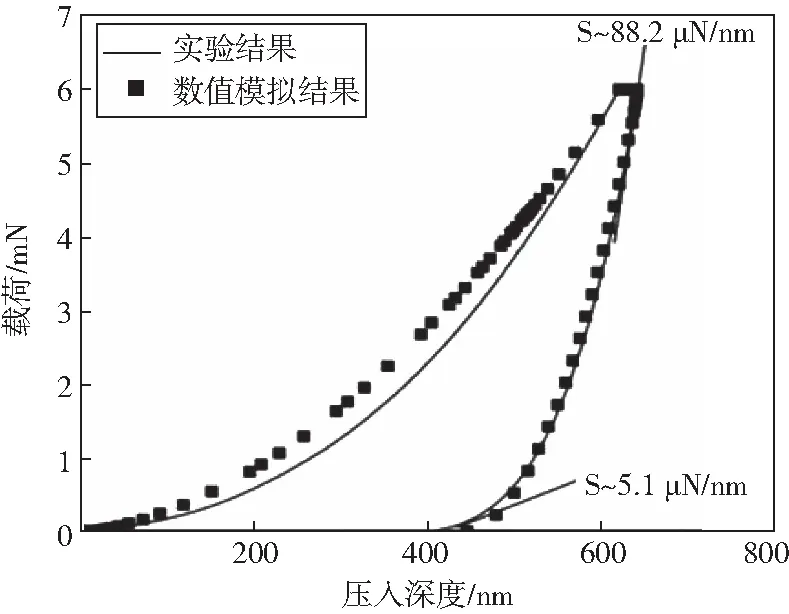
图4 外层牙本质的载荷压入深度曲线

数值模拟不仅描述了卸载曲线与加载曲线不重合现象，而且还准确描述了卸载过程中的刚度降低现象。这证明该数值模型能够有效描述在压痕作用下的力学行为。图5表明与压头接触区域的牙本质受到损伤最严重。并且随着牙本质深度的增加，损伤加重。

图5 纳米压痕作用下牙本质在内层、中层质和外层区域的损伤分布

3 讨论

本文建立了牙本质的塑性损伤力学模型并研究了在压痕载荷作用下其塑性及损伤力学性质，分析其力学性能随牙本质深度的变化。牙本质的纳米压痕实验结果表明，中层和外层牙本质的抵抗变形能力高于内层牙本质抵抗变形的能力。这与本文数值模拟预测的牙本质屈服强度随牙本质深度的变化是一致的。即内层牙本质屈服强度低与中层和外层牙本质的屈服强度。此外在相同载荷作用下，中外层牙本质更不容易发生损伤。压痕实验过程中牙本质刚度下降是由于牙本质发生损伤，这种损伤是以其内部的微裂纹为主要形式的微损伤[10]。当牙本质受到外载荷作用时，这些微裂纹萌生于牙本质小管附近，然后发生扩展。而牙本质小管之间的管间牙本质可显著减少这些微裂纹的扩展。因此牙本质小管的微观结构对损伤力学性能影响很大。而先前的研究表明：内层牙本质小管的直径和密度大于中层和外层牙本质小管的直径和密度。例如外层牙本质小管直径和密度约为0.9 μm和20 000 tubules/mm2，而在靠近牙髓腔处约为2.5μm 和45 000 tubules/mm2[11].这就解释了中层及外层牙本质更易抵抗损伤。

牙本质的这种力学性质与其功能有关。作为牙齿中体积分数最大的部分，其具有充当牙釉质基底的作用，并且可有效保护牙髓腔不受外界刺激。当牙齿受到外载荷作用时，载荷作用在牙釉质上并将其传递给牙本质。而外层的牙釉质具有很高的刚度，处于外层的牙本质需要较大的刚度减小牙釉质的变形。

牙本质在纳米压痕实验结果表明，其在卸载的初始阶段和最后阶段刚度出现明显的下降。以外层牙本质为例，其在卸载的初始和最后阶段的接触刚度分别为88.2 μN/nm和5.1 μN/nm.即在卸载过程中接触刚度下降约90%.本文建立的塑性损伤模型可以很好的解释这种现象。如图6所示，在压痕实验测试卸载初始阶段与最后阶段，压头与牙本质的接触半径比值为3∶1，即接触面积比约为9∶1.而图5表明损伤主要发生在压头压入点附近。当压头和牙本质接触面较大时，即卸载的初始阶段损伤对刚度的影响比较小，而在卸载的最后阶段，其接触面很小，接触处的损伤都比较大，此时计算的刚度可认为是牙本质发生损伤后的刚度。Berkovich压头的纳米压痕测试弹性模量为:

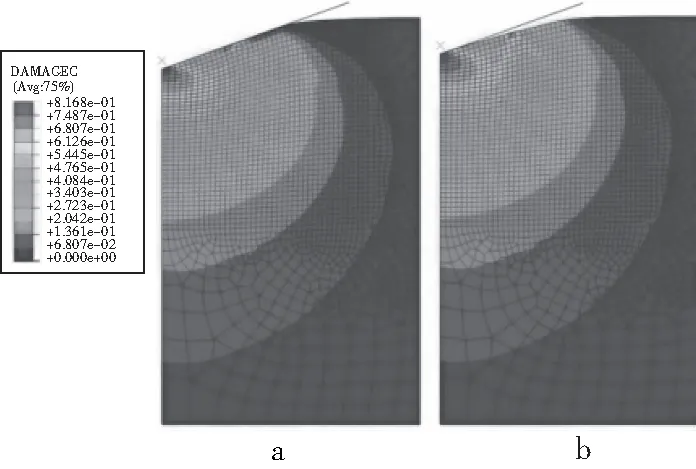
图6 纳米压痕测试(a)卸载初始时刻与(b)卸载结束时刻压头与试样的接触状态

(10)

根据公式(10)，计算可得牙本质在卸载最后阶段的弹性模量是其在卸载初始阶段计算弹性模量的15%～20%，这与压头附近的损伤最大值约为0.8一致。