基于LSTM 神经网络的大宗农产品价格预测研究

袁铭涓 孙若莹

北京信息科技大学，北京 100192

随着我国经济的快速发展，大宗商品交易市场受到了广泛而密切的关注。期货交易在固定的场所或平台按照既定标准进行买卖合约，到期交割现货。现货价格是期货价格的基础，期货价格能够发现到期日现货市场的预期价格，二者具有长期协整关系。

我国作为农业大国，大宗农产品期货在我国期货市场的交易中盘踞绝对的优势，大宗农产品价格关系着国计民生，也是农产品期货市场稳定发展的根基。近年来大宗农产品价格变化较大，不稳定性加剧，价格风险日益增加。影响大宗农产品价格产生变化的要素主要有两方面：一方面是人们根据农产品交易的历史价格，凭借经验进行商品定价，使得大宗农产品价格序列呈现出一定的历史相关性；另一方面是由于政策变动、自然灾害等情况引发的市场需求萎缩、资金短缺等现象，也导致农产品价格在短期内呈现出波动大、非平稳的特点[1]。这些影响因素难以被量化，却通过价格数据序列中突然变化的拐点体现了其作用。

因此，挖掘商品期货价格规律，对未来农产品价格走势进行更加精确的预测，对于政府、金融投资者、大宗交易商的决策都十分重要和关键。首先，有利于提高中国在国际大宗农产品期货市场的地位，指导我国大宗农产品定价市场化改革方向；其次，有利于帮助政府制定相关价格调控政策，强化期货市场监管，促进期货现货市场有效联动，维护金融交易市场的稳定发展；最后，能够对未来市场行情走势进行合理分析和评估，从而进一步指导大宗商品现货交易链中的企业进行加工贸易或销售等经营活动，规避风险、降低成本，获取最大化收益。

通过梳理近年来国内外研究文献可以得知，学者们对价格进行预测的研究方法大致可划分为线性、非线性两大类模型[2-3]。线性模型主要包括一些计量学模型和统计学模型，例如向量自回归模型（Value at Risk，VAR）、自回归条件异方差模型（Autoregressive Conditional Heteroskedasticity，ARCH）、差分自回归移动平均模型（Autoregressive Integrated Moving Average，ARIMA）等。其中，卢虎生等[4]运用VAR模型分析了氧化钕价格的影响因素，并对其价格进行了预测。吴玉霞等[5]利用ARIMA 对股票价格进行了预测研究。方燕等[6]基于由ARCH拓展出的GARCH 模型，结合ARIMA 对沪深两市的传媒板块指数价格进行了分析预测。

由于大宗商品价格常常呈现不规律的波动状况，导致线性模型在预测期货价格时显得有些力不从心。近年来，以机器学习模型为代表的，例如决策树模型、支持向量回归模型（Support Vector Rregression，SVR）、随机森林（Random Forest，RF）等非线性模型在处理、挖掘变量之间的非线性关系、以及预测准确性上比线性模型表现得更有优势，近年来在价格预测方面的应用越来越普及。BasakS[7]等使用贝叶斯模型对股票市场的价格进行了预测研究。沈金榕[8]基于决策树算法研究了某上市公司的财务指标，并对收益进行了预测。张宝文等[9]等结合混沌性时间序列与SVR 模型对玉米价格进行了预测。

本文根据大宗农产品期货价格的典型时间序列特征，构建了基于LSTM 神经网络的大宗农产品价格预测模型，选取2018—2021 年的大豆期货价格数据，并在数据处理、模型建立、参数调整等方面进行了相关研究，与ARIMA 模型相比，证明了LSTM 神经网络在预测期货价格方面具有更好的预测效果。

1 研究方法

1.1 RNN 网络

神经网络是由多个连接单元或节点构建的网络模型，当一个神经元接收到信号时并对信号进行处理后，再传递给其相连接的下一个神经元。传统的神经网络没有记忆功能，只关注当前时刻的处理，不关注前一时刻处理的信息是否可以在下一时刻使用。为了解决这个问题，循环神经网络RNN 应运而生。RNN 在神经元之间建立联系，对隐藏层的中间结果进行循环利用，使得神经网络能够从时间维度上提取到有用的信息[10]。RNN 循环神经网络结构如图1 所示。

图1 RNN 循环神经网络结构

其中X和h分别对应在0—t时刻模型的输入和输出，A为模型的隐层处理部分，在层之间都有相对应的权重U、V、W。t时刻的输出结果不仅与Xt有关，还与上一时刻的输出信息有关，但随着时间序列长度的增加，网络中的Sigmoid 激活函数逐渐抵达饱和，输出信息没有明显变化，在反向传播时就会爆发梯度消失。

1.2 长短期记忆神经网络

LSTM 神经网络模型最早由Hochreiter 等[11]于1997 年提出，后由Graves 等[12]在2012 年进行改进，是一种广为人知的特殊的RNN 模型。LSTM 引入了长时间信息有效性的机制，通过增加存储长期有效数据的单元（cell），引入可控自循环的门（gate），从而克服了RNN 模型存在的梯度消失和梯度爆炸问题，提升了预测能力。LSTM 神经网络结构如图2 所示。

图2 LSTM 神经网络结构

LSTM 神经网络模型由输入层、输出层和一个或多个隐藏层组成。每个神经元包括遗忘门（forget gate）、输入门（input gate）、输出门（output gate）和存储单元（cell），每个门都实现各自不同的功能[13]。遗忘门确定从单元状态中摒弃多少信息；输入门确定哪些信息添加到单元状态中；输出门确定哪些单元状态信息作为输出。记忆单元与其他模块的连接处存在权值，所有的记忆单元都通过上述三个门组成的门限机制进行控制。LSTM 的前向传播流程步骤如下：

①计算从之前的单元状态中Ct-1需要删除的值ft。

LSTM 神经网络根据上述计算步骤来处理每个时间步长为t的输入序列，当处理完序列最后1 个元素后，返回整个序列的最终输出。

1.3 差分自回归移动平均

ARIMA 模型是一种著名的时间序列预测方法，最早由C.P.Box 和G M.Jenkins[15]提出。其中，AR 是“自回归模型”，p是自回归项的个数；MA 为“移动平均模型”，q是移动平均的项数；d是使模型成为平稳序列的差分次数，也称作阶数[5]。其中，p阶自回归过程AR (p)的一般表达式如下所示：

2 实证研究

2.1 实验环境及预测流程

基于Python3.7 语言环境，本文在实证部分选用非线性模型中的长短期记忆网络模型LSTM，采用Keras 框架构建价格预测模型，并选取传统计量学模型中的差分自回归移动平均模型ARIMA，分别对同一组大豆期货行情价格数据进行训练。两模型的预测流程如图3 所示。

图3 LSTM、ARIMA 模型预测流程

2.2 数据集来源

本研究数据来源于investing 财经网站—大连商品交易所大豆2 号期货行情数据，时间跨度为2018 年3月19 日—2021 年4 月19 日，通过在大连商品交易所查询大豆2 号期货合约可知，其交易时间为每周一至周五，因此有效数据共751 天，数据集共包括收盘价、开盘价、最高价、最低价、交易量、涨跌幅等6 个维度，原始数据集形式如表1 所示。

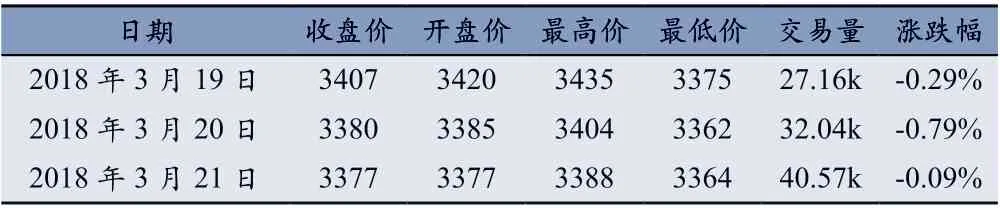
表1 原始数据集形式

2.3 数据预处理

2.3.1 训练集、测试集划分

将原始数据集划分为7：3 的比例，选取70%作为模型的训练集，30%作为测试集。将模型在时间线上的训练结果与真实价格数据进行对比，以判断预测结果的准确程度。

2.3.2 异常值、缺失值处理

将搜集到的原始数据中的异常值、缺失值进行预处理，处理原则是把前一天和后一天的价格数值进行相加取平均值。将所有数据处理完毕后，取开盘价、收盘价、最高价、最低价等4 个维度的数据，大豆在整个周期内的价格变化趋势如图4 所示。

图4 大豆期货价格变化趋势

2.3.3 数据归一化

在将原始数据输入LSTM 神经网络模型进行训练前，对其进行Min-Max Normalization 归一化，将对应原始值映射到[0，1]之间，计算公式为：

2.4 LSTM 模型构建

2.4.1 基本参数

LSTM 模型中主要包括网络层数、神经元个数、迭代次数、样本数等参数。在网络训练过程中，epoch指向前和向后传播中所有批次的单次训练迭代次数；time_step 表示每个样本内包含有多少个时刻；而batch_size 定义为更新内部模型参数之前进行批处理的样本数。单层LSTM 网络模型预测准确率较低，通过增加网络层数有利于提高模型预测准确率，但过度增加网络深度会增加计算冗余度、延长模型训练时间，存在梯度消失的风险及过大的训练误差[16]。

考虑到数据本身特点以及业务需求，本研究中的神经网络模型的层数设计为两层，两层网络的神经元数分别设为128 和100，并将时间窗口移动步数设置为1，即选用过去n天的价格来预测未来1 天的价格，以期望模型获得最佳预测效果。

2.4.2 参数调优

为提高模型预测的准确性，对LSTM 模型中的epoch、time_step 和batch_size 参数的最佳组合进行探索。在模型参数调优实验中，对random.seed()函数和Shuffle()函数进行处理，以期望最大程度地消除数据随机性打乱对结果的影响，提高结论的可靠性。使用MSE（均方误差）作为评价指标对模型准确率进行考量，MSE 函数一般用来检测模型预测值和真实值之间的差异程度，MSE 越小代表着模型准确率越高，计算公式如下所示：

利用控制变量法对LSTM 网络模型中的三个重要参数：n_steps、batch_size 和nb_epoch 的最佳参数组合进行测试，测试结果如图5 所示。

图5 不同参数组合的MSE 值

2.4.3 模型预测

根据不同参数组合的实验结果，选取最佳的参数组合n_steps=80、batch_size=500 和nb_epoch=60。将数据随机打乱输入模型进行训练，每次输入的数据将作为模型输入特征（Xfeature），预测的价格作为模型标签（Ylable），LSTM 模型预测结果如图6 所示。

图6 LSTM 模型预测结果

2.5 ARIMA 模型构建

2.5.1 预测步骤

①将价格数据集中的异常值、缺失值进行数据预处理。

②对序列进行平稳性检验，检验结果P-value 大于0.05，说明原序列属于非平稳序列，应当对该序列做d阶差分运算，直至序列平稳，经检验该序列为一阶。

③运用AIC 或BIC 准则对模型进行定阶，得到p=0，q=0，建立ARIMA(0，1，0)模型。

2.5.2 模型预测

使用拟合后的有效模型ARIMA（0，1，0）对大豆期货价格进行预测，将历史数据按照7：3 的比例划分成训练集和测试集，ARIMA 模型预测结果如图7所示。

图7 ARIMA 模型预测结果

2.6 结果比较

针对以上实验可知，对于不平稳的时间序列数据，例如期货价格数据，ARIMA 模型在训练的过程中极容易存在显著噪声，一旦价格在某个区间内出现大幅度的变动，ARIMA 便难以学习到价格的变动规律，预测效果极差。而作为RNN 的一种改进模型，LSTM 可以解决训练过程中的梯度消失和梯度爆炸问题，与传统的预测研究方法相比，模型的预测结果与数据真实值之间的偏差较小，并且通过调整训练次数、批处理样本数等LSTM 模型的具体参数，可以在一定范围内提高预测精度。另外，对比前文中将seed()函数和Shuffle()函数进行处理后的MSE 值，模型训练后的MSE 结果=0.0038＜0.0168，预测准确率得到了大大提升，说明随机打乱数据能够使得训练更切合数据的真实分布，从而进一步提高LSTM 模型在预测方面的泛化能力，充分展现了LSTM 在处理此类时间序列数据方面的优越性和可行性。

3 结 语

本文根据大宗农产品期货价格数据的特点，利用LSTM 神经网络模型对其进行了价格预测，并将预测结果与ARIMA 模型的预测结果进行比较。实验结果表明，LSTM 神经网络模型在价格预测方面具有较好的性能，在未来对大宗商品交易商制定价格策略、规避价格风险等方面具有一定的适用性和参考性。鉴于神经网络具有强大的自我学习能力、良好的泛化能力以及高度可调节性，本研究在未来可以有进一步改进。

大宗商品价格波动的表象中蕴含着多方面的影响因素以及复杂的传递过程，考虑到数据收集及量化的难度，本实验仅选取了大豆期货价格作为模型训练的数据，通过单步预测实现了对大豆价格的短期预测。未来应收集更长时间跨度的大豆价格数据，同时对影响价格的特征因素做进一步量化研究，在数据充分的基础上对中长期的价格预测进行完善。

考虑到企业实际业务的需求，本模型可以应用到其他农产品期货的预测中，从而进一步证明模型的普适性。同时应探索其他在时间序列数据处理上具有优势的机器学习模型，结合LSTM 神经网络形成集成模型，使模型能够更好地学习到其价格波动的深层规律，以进一步提高模型的预测准确度，给企业带来更加有价值的参考。