基于随机森林和支持向量机的高性能混凝土抗渗性预测研究

吴贤国，刘 茜，王洪涛，陈虹宇，高 飞，黄汉洋

(1.华中科技大学土木与水利工程学院，武汉 430074；2.中建三局集团有限公司,武汉 430000； 3.南洋理工大学土木工程与环境学院，新加坡 639798；4.中建商品混凝土有限公司,武汉 430000)

0 引 言

抗渗性是混凝土的主要性能之一，直接影响混凝土结构的耐久性和使用寿命。在实际工程中，氯离子渗透及其对钢筋的相对腐蚀是导致钢筋混凝土基础设施恶化的主要原因，而氯离子渗透对混凝土的损伤程度由混凝土的抗渗性决定，因此，针对混凝土抗渗性进行研究具有重要的工程意义。

目前，众多专家学者对混凝土抗渗性进行了深入研究，并取得了一些研究成果。张瑞稳[1]基于正交试验，研究了早龄期混凝土高温作用后力学性能及抗渗性的变化。王德志等[2]研究了氯盐冻融作用下，不同粉煤灰掺量对混凝土抗渗、抗冻性能的影响。宁逢伟等[3]通过微观测试手段，分析了膨胀剂和硅灰改善C50喷射混凝土抗渗性的机理。梁敏飞等[4]在材料试验和数值模拟的细观模型基础上，对混凝土的抗渗性进行了研究。张岩等[5]通过试验研究了水胶比对塑性混凝土的抗压性能、变形性能和抗渗性等主要性能的影响。Fan等[6]通过制备不同长径比和钢纤维含量的钢筋来提高超高性能混凝土(UHPC)试件的强度，从而对UHPC抗渗性进行了研究。Liu等[7]通过添加纳米SiO2等材料来研究其能否改善普通水泥-粉煤灰体系混凝土的抗渗性。Xiao等[8]基于试验测试探讨了纳米SiO2对不同骨料级配混凝土微观结构和抗渗性的改善效果。上述研究主要基于试验对混凝土抗渗性进行研究分析，不仅费时费力，而且由于混凝土抗渗性试验研究中不确定性因素很多，测试数据存在离散性、随机性和一定误差，使得分析结果往往与实际工程之间存在偏差。

混凝土抗渗性与许多影响因素相关，要提高抗渗性预测结果的准确性，必须有效剔除不重要的冗余因素。为此，本文将随机森林(RF)算法和支持向量机(SVM)结合，提出一种基于RF-SVM模型的混凝土抗渗性预测模型。首先利用RF可以筛选关键指标的特点，结合向后剔除法对不重要指标进行剔除，得到混凝土抗渗性预测的最优指标体系，然后在此基础上构建了基于SVM的混凝土抗渗性预测模型，以实现对混凝土抗渗性的精确预测。

1 理论和方法

1.1 随机森林理论

随机森林(RF)是CART树和Bagging相结合形成的一种综合算法，在2001年由Breiman提出，可以用于处理分类和回归问题，广泛用于预测和特征选择等问题[9-10]。Bagging(Breiman 1996)是一种基于统计学中bootstrapping思想的综合学习方法，在Bagging中，通过bootstrapping没有被用于建立RF模型的数据称为袋外数据(OBB)。假设数据量为b个，特征变量有k个，每个袋外数据的均方误差依次为RMSE1,RMSE2,…，RMSEb，标准误差为RSE，对每个特征变量进行随机置换得到新的袋外数据集，计算新的袋外数据集的均方误差，重复进行上述操作直到在袋外数据中对所有特征变量都进行了置换，并得到了如下误差矩阵A[11]：

A=(RMSE11…RMSE1b⋮⋱⋮RMSEk1…RMSEkb)

(1)

将RMSE1,RMSE2,…,RMSEb与误差矩阵中的对应行向量相减，取其平均值除以标准误差RSE，从而得到特征变量的重要性评分Ui为：

Ui=[(∑bj=1RMSE-RMSEij)b]RSE， (1≤i≤k)

(2)

式中：j表示误差矩阵A中向量的列数。

1.2 支持向量机理论

支持向量机(SVM)作为一种智能算法，能够很好地学习输入与输出参数之间的关系[12]。对于非线性回归问题，支持向量机可以引入一个非线性映射函数φ(x)，它可以将一组非线性关系数据中的输入输出变量(xi,yi)一一映射到高维特征空间中，然后利用核函数在高维特征空间进行线性回归模型的建立，从而很好地解决非线性问题[13]。设定一组样本集，假设样本内输入因素(自变量)xi和输出因素(因变量)yi呈线性函数关系，则回归预测的输出值f(x)的计算如式(3)所示：

f(x)=WTx+z

(3)

式中：WT为xi的权重系数向量；z为对xi赋予权重乘积后所发生的偏置数；x为输出变量。式(3)可转化为二次规划的优化问题，表达式为：

min12||ω||2+C∑li=1(ξi+ξ*i)

(4)

式中：ξi和ξ*i为松弛变量；C为其惩罚系数；ω为权重。当核函数K(xi,xj)=φ(xi)·φ(xj)时，在映射到高维特征后的优化问题即变为[14]：

min∑ni,j=1(αi-α*i)(αj-α*j)K(xi,xj)+ε∑ni=1(αi+α*i)-∑ni=1yi(αi-α*i)

(5)

s.t. {∑ni=1(αi-α*i)=0 0≤αi,α*i≤C

(6)

式中:αi和α*i为Lagrange乘数；xj为输出变量；ε为允许误差。由此便可求解出非线性支持向量回归机的函数表达式为：

f(x)=∑ni=1(αi-α*i)K(xi,xj)+z

(7)

2 RF-SVM预测模型

为了快速有效地对混凝土抗渗性进行准确预测，提出一种基于RF-SVM的混凝土抗渗性预测模型。如图1所示，该模型的建立主要分为两个步骤：(1)基于RF的混凝土抗渗性指标筛选；(2)基于SVM的混凝土抗渗性预测。利用RF对特征指标进行筛选后再进行SVM的回归预测，能够提高决策的可靠性和有效性。

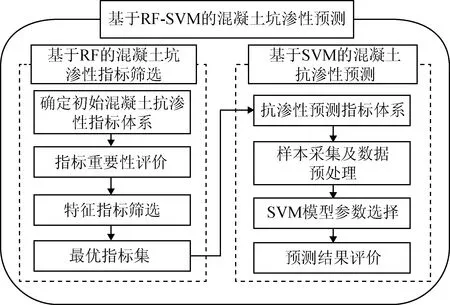
图1 基于RF-SVM的混凝土抗渗性预测模型Fig.1 Prediction model of impermeability of concrete based on RF-SVM

2.1 基于RF算法的混凝土抗渗性指标筛选

2.1.1 建立初始指标体系

根据文献分析和工程经验总结[15-16]，从混凝土原材料配合比层面考虑，选取水泥用量、减水剂用量、粉煤灰用量、针状及片状颗粒总含量、细集料用量、粗集料用量、硅灰用量、平均粒径、含泥量、水胶比、碱含量、砂率和用水量等因素，以氯离子扩散系数为评价混凝土抗渗性的输出指标，建立混凝土抗渗性分析初始指标体系。

2.1.2 混凝土抗渗性指标筛选

初始指标体系直接用于建立预测模型容易导致过拟合，不一定能够得到最好的预测精度，所以还要对初始指标进行剔除，筛选出用于预测模型建立的最优指标集。本文将RF算法与后向剔除法结合起来对初始特征指标作出剔除筛选，通过对初始特征指标筛选后，得到的最优指标组合将直接作为后文模型的输入变量，以提高SVM建模的预测精度。

在基于初始指标体系对特征指标筛选剔除时，首先要确定RF模型的两个参数指标mtry和Ntree的取值，mtry为决策树进行随机特征分割的特征数量，一般取输入特征指标的1/3。Ntree为决策树的棵数，一般在大于500时即可得到稳定的预测误差。为了提高预测精度，本文采取交叉验证的方式进行模型精度验证。

2.2 基于SVM模型的预测

2.2.1 样本采集及数据处理

将RF筛选结果作为SVM建模的指标体系，基于此收集相关数据并整理后形成数据样本集。在模型建立之前，为了消除不同特征指标的数据因为量纲不同所带来的影响，有必要对初始数据进行归一化预处理，以统一变量维度，降低模型的训练难度，防止模型精度下降或者网络无法收敛。归一化的方式有很多，如将数据归一化到[0,1]或[-1,1]区间内，本文选择把样本输入数据归一化到区间[0,1]上，数据归一化后的值计算表达式如下:

=xi-xminxmax-xmin

(8)

式中：xi表示输入或者输出数据;xmax表示变换特征数据的最大值;xmin表示变换特征数据的最小值。

2.2.2 SVM模型参数选择

核函数是将一组非线性关系的数据映射到高维特征空间中的关键，它对SVM的效能有很大的影响，因此有必要对核函数进行合理的选择。径向基核函数(RBF)是目前SVM模型中最常用的核函数，具有很好的抗干扰能力以及局部性，且适用于非线性问题，因此本文选择SVM预测模型的核函数为RBF核函数F(x,xi)，其表达式如下：

F(x,xi)=exp(-||x-xi||22δ2)

(9)

式中：xi为输入变量；x为输出变量；δ为函数的宽度参数。

为了防止SVM模型出现欠学习问题，同时保证模型良好的泛化能力，本文选择网格搜索法对RBF核函数的惩罚系数C及核函数参数g进行参数全局搜索，以得到全局最优解，并在网格搜索法的基础上，结合K折交叉验证方法，对所有可能的参数进行验证，找出精度最高的模型所对应的参数，从而确定最终的优选参数。

2.2.3 预测结果评价

为了对SVM预测模型的预测结果进行有效评价，同时引入均方误差(RMSE)和拟合优度(R2)两个指标对预测结果做出评价，RMSE用来衡量预测值与实际值之间的偏差，而R2用于评估预测值与实际值之间的拟合程度。两个评价指标的计算公式如下：

RMSE=∑ni=1(yobs-ypred)2n

(10)

R2=1-∑ni=1(yobs-ypred)2∑ni=1(yobs-obs)2

(11)

式中:yobs表示实际值;ypred表示预测值;obs表示实际值的平均值；n表示数据集的个数，即有n组预测值和实际值。

为了进一步验证预测结果是否满足工程实践的要求，根据式(12)计算出预测值与实际值的相对误差E。

E=|Y-SS|×100%

(12)

式中：S表示试验实际值;Y表示预测值，若平均相对误差小于6%，则认为满足工程实践的要求。

3 实例分析

3.1 工程背景

我国东北某高速公路项目位于高寒高盐碱地区，对混凝土抗渗性要求较高。因此，本文以C50混凝土为研究对象研究混凝土抗渗性，基于正交试验和现场抗氯离子渗透加速试验，获取混凝土配合各参数及氯离子渗透系数的数据样本，其中氯离子渗透系数为28 d氯离子渗透系数，一共收集了116组混凝土抗氯离子渗透试验数据作为样本集，部分数据如表1所示。

表1 混凝土抗氯离子渗透试验部分数据Table 1 Partial experimental data of chloride ion permeation resistance of concrete

3.2 基于RF算法的混凝土抗渗性指标筛选

3.2.1 指标重要性排序

根据2.1节所述，利用RF算法对混凝土抗渗性初始特征指标进行重要性排序，结合后向剔除法对特征指标进行筛选，从而得到用于SVM建模的最优指标组合。通过在R语言软件中，载入RF程序包，用于RF模型的构建，对初始特征指标进行重要性评分，根据式(2)对表1中的数据进行计算，可以得到各特征指标的重要性排序结果，如图2所示。由图2可以看出，经过计算重要性排在前两位的特征指标依次为水胶比、水泥用量，从工程实践经验来看，水胶比的变化对混凝土耐久性的影响最为明显，而水泥用量跟水胶比存在很大的相关性，因此RF算法得到水胶比和水泥用量的重要性排在前面的结论合理。

图2 指标的重要性排序图Fig.2 Importance ranking chart of indexes

图3 不同特征指标组合时RMSE变化趋势图Fig.3 RMSE change trend chart under different combination of characteristic indexes

3.2.2 关键指标筛选

根据2.1节所述，确定RF模型的两个参数指标取值,mtry为4，Ntree为600，同时采取10折交叉验证来检验模型的精度。在重要性排序结果的基础上进行指标后向剔除，得到不同特征指标组合时均方误差RMSE的变化趋势,如图3所示。

由图3可以看出，整体上RSEM呈现出先下降后上升的趋势，这说明了随着一些不重要指标被剔除后，模型的预测精度得到有效提高；当特征指标组合的个数达到某一值时，再继续对特征指标进行剔除时会导致模型预测精度下降，这说明进一步剔除特征指标会误删掉一些重要的特征指标。当特征指标组合中的指标个数为6时，均方误差值最小，模型精度最高。从整体上讲，将RF算法与向后剔除法相结合对初始特征指标作出剔除筛选，能够有效剔除无关的特征指标，进而提高模型的预测精度。结合图2筛选出的最优特征指标集如表2所示。

表2 混凝土抗渗性预测模型输入及输出指标Table 2 Input and output indexes of prediction model for impermeability of concrete

3.3 基于SVM模型的预测

3.3.1 样本数据获取与预处理

在3.2节指标筛选结果的基础上，确定SVM预测模型输入特征指标为水胶比、水泥用量、粉煤灰用量、细集料用量、粗集料用量、减水剂用量，将氯离子扩散系数作为输出指标，通过现场加速试验，收集一共116组混凝土抗氯离子渗透试验数据作为样本集，部分数据见表1。对输入和输出特征指标数据进行归一化处理，将全部样本随机抽取93组样本构成训练集以训练模型，为了检验模型的泛化性能，将余下23组样本作为测试集来验证模型效果。

3.3.2 模型参数优化

图4 参数优化结果3D视图Fig.4 3D view of parameter optimization results

基于MATLAB平台加载SVM工具箱，选择网格搜索法结合5折交叉验证法(5-CV)对SVM模型的参数进行选优。将惩罚系数C的取值范围设置在[2-8,28]之间，步距大小为每次将幂指数增加1的以2为底的幂指数，惩罚系数C的取值即为2-8、2-7、…27、28，核函数参数g的取值范围设置与惩罚系数C相同。参数优化结果的3D视图如图4所示。由图4可知，惩罚系数C的最优值为5.278，核函数参数g的最优值为0.574 35，此时均方误差为0.000 300 18。说明惩罚系数C为5.278，核函数参数g为0.574 35时，在5-CV验证后的均方误差值最小。

3.3.3 预测结果评价

根据参数优选结果建立混凝土抗渗性预测模型，利用此模型分别对训练集和测试集进行拟合和预测。图5为混凝土抗渗性预测模型对训练集数据的预测结果，从图中可以看出，该模型通过对训练样本的训练，拟合结果很好，说明该模型对输入与输出之间的决策规律进行了充分学习，其预测值与实际值之间误差非常小。图6为该训练模型对测试集样本的预测结果，从图中可以直观地看出，混凝土抗渗性SVM预测模型得到的预测值非常贴近实际值，预测效果很好。经计算，训练集中实际值与预测值之间的均方误差为0.000 3，拟合优度为0.998,测试集中实际值与预测值之间的均方误差为0.000 4，拟合优度为0.996。均方误差越接近于0，拟合优度越接近于1，表示预测效果越好，可以说明该模型对混凝土抗渗性的预测效果良好，且具有较好的泛化能力。

为了进一步验证预测结果是否满足工程实践的要求，根据公式(12)计算测试集的预测值与实际值的相对误差。计算得到测试集中最大相对误差为4.60%，最小相对误差为0.03%，平均相对误差为1.107%，在6%以内，可以满足工程实践中对误差的要求。

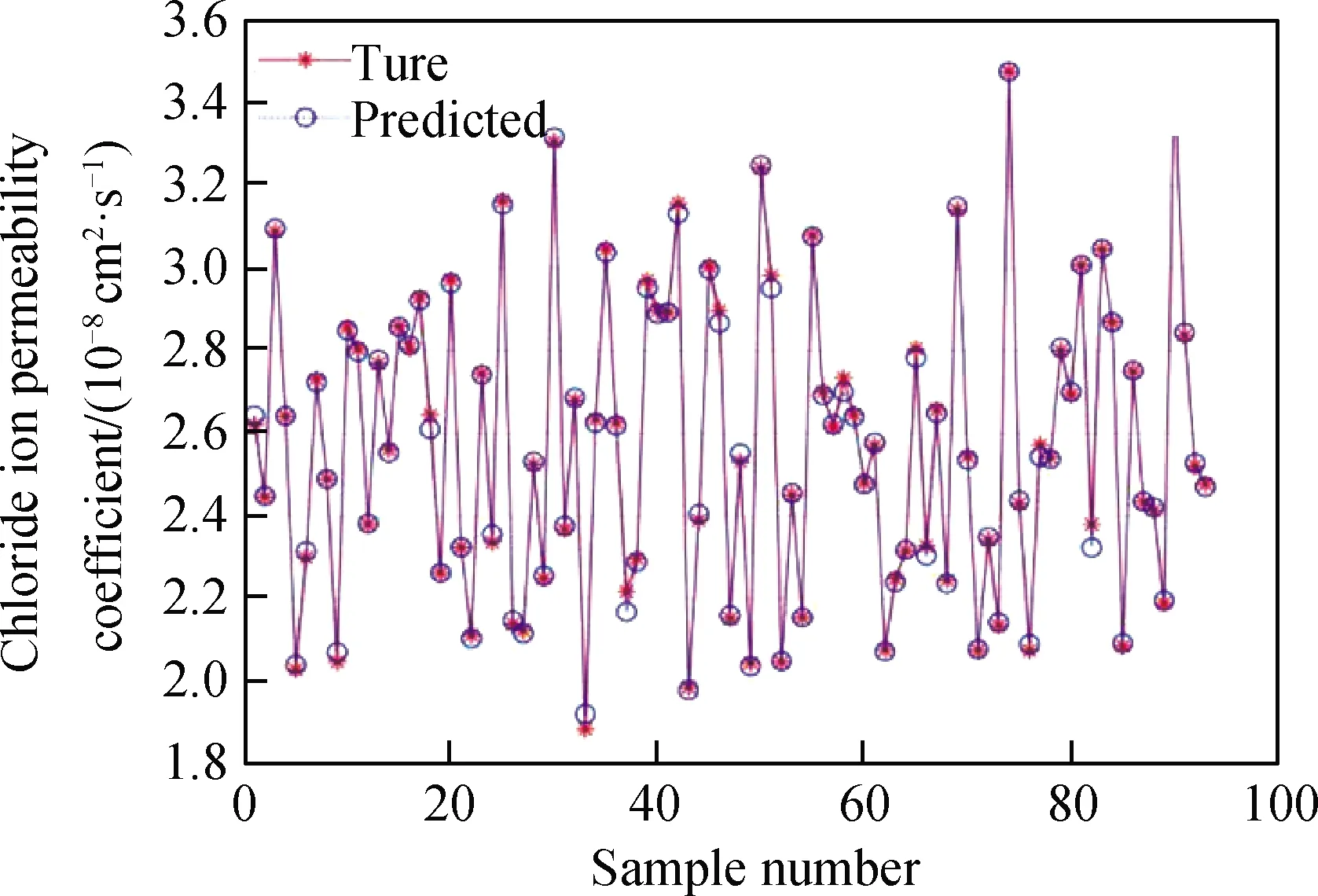
图5 抗氯离子渗透模型训练集预测结果对比Fig.5 Comparison of prediction results of training set of chloride ion permeation resistance model

图6 抗氯离子渗透模型测试集预测结果对比Fig.6 Comparison of prediction results of testing set of chloride ion permeation resistance model

4 结 论

(1)本文建立了一种基于RF-SVM的混凝土抗渗性预测模型，该模型首先利用RF算法对混凝土抗渗性的多个影响因素进行指标筛选，得到最优指标集作为SVM模型的输入指标，从而剔除了冗余指标，提高了混凝土抗渗性预测模型的预测精度。

(2)以东北某高速公路项目为背景，基于RF算法进行混凝土抗渗性指标筛选，剔除冗余指标后得到的最优指标集包括水胶比、水泥用量、粗集料用量、细集料用量、减水剂用量和粉煤灰用量，为基于SVM模型的混凝土抗渗性高精度预测提供了条件。

(3)通过现场混凝土抗氯离子渗透试验获取样本数据，将氯离子扩散系数作为抗渗性评价指标，在最优指标集的基础上建立了混凝土抗渗性预测模型。预测结果的最大相对误差为4.60%，最小相对误差为0.03%，平均相对误差为1.107%，预测结果精度较高且满足工程实践的要求，说明该预测模型具有不错的泛化性能，验证了RF-SVM模型在混凝土抗渗性预测中的可行性及有效性。