深部冻结井筒内壁早期温度-应力场演化特征研究

2021-04-17张基伟李方政喻新皓孔令辉

煤炭科学技术 2021年2期

张基伟，李方政，喻新皓，丁航，孔令辉

（1.煤炭科学研究总院建井研究分院，北京 100013；2.天地科技股份有限公司，北京 100013；3.北京中煤矿山工程有限公司，北京 100013）

0 引言

人工冻结法施工是井筒穿越深厚冲积层、表土层、富水砂层的主要施工方法之一，已经广泛应用于深部井筒建设中［1-4］。目前，冻结井筒广泛采用的井壁结构为双层钢筋混凝土塑料夹层复合井壁，其中，自下而上连续浇筑的内层井壁是冻结壁解冻后抵抗静水压力与防渗的主要结构［5］。然而，随着井筒深度不断增大直至千米，冻结井筒内壁厚度相应增大。根据现行规范，千米以深内层井壁厚度将超过2 m［6］。文献［7-9］均发现内层井壁厚度的增加或混凝土强度等级增加均会导致早期水化放热更高。程桦等［10］认为，因外部冻结壁持续供冷条件下C60 以上高强内壁混凝土水化放热导致内外壁温差较大，在井壁内形成约束温度应力，当温度应力大于混凝土抗拉强度时，将会产生早期温度裂纹（缝）。但该文献中未明确内壁大体积混凝土浇筑后形成的早期温度应力影响范围及大小。可见，目前仍需要进行深部冻结井筒内壁大体积混凝土早期温度应力相关研究，为科学预防冻结井筒破裂提供理论依据。

众多学者开展了井壁温度应力理论等相关研究，并取得很多研究成果。文献［11-13］基于热弹性理论分析了内外井壁温差变化下井壁各向应力分布情况，认为内外井壁温差引起的温度应力值最大。何朋立［14］将冻结井筒温度应力分为井筒内、外壁温差产生的温度应力与井筒径向膨胀受阻产生的温度应力2 部分，并推导了相应的解析解。管华栋等［15］基于热弹性理论，建立了冻结井壁早期温度应力计算模型。张红亚［16］利用ANSYS 软件模拟冻结井筒外壁温度场与应力场分布规律，发现外层井壁早期径向温度应力主要为拉应力，拉应力在浇筑后逐渐增大，并在浇筑后5 ～6 d 开始出现拐点，随后拉应力逐渐减小直至全部变为受压。张涛［17］采用ADINA 程序进行了冻结内层井壁早期温度场和温度应力数值计算，但是将内外壁之间塑料板约束简化为径向位移约束，与现场实际情况有较大差距。以上成果为冻结井壁混凝土温度应力研究奠定了坚实的理论基础，但是均缺少考虑内热源、外部冷源、塑料板摩擦约束、上覆井壁荷载和地层侧压力等多种热-力边界条件的冻结井筒内壁大体积混凝土早期温度-应力场演化特征相关研究。

笔者以红庆河煤矿一号风井内壁为工程背景，研究深部热-力耦合条件下冻结井筒内壁早期温度应力相关理论，提出考虑多种边界条件的内壁大体积混凝土热-力耦合方法。将获得的混凝土温度、应变结果与现场检测结果进行对比。旨在掌握深井内壁大体积混凝土早期温度-应力场演化特征，寻找易出现早期温度裂缝的高风险区。为内壁大体积混凝土早期温度裂缝防治提供理论依据。

1 工程背景

红庆河煤矿一号风井冻结深度689 m，井筒净径7.6 m，掘砌荒径11 m。井筒穿过的地层主要为第四系、白垩系和侏罗系地层，白垩系平均厚度为534.23 m，侏罗系地层平均厚度为390.32 m。冻结壁设计厚度3.7 m，积极期最低盐水温度-28 ～-32 ℃，冻结壁有效平均温度-10 ℃。主冻结孔布置圈径16.2 m，开孔间距1.374 m，孔数目37 个，孔深689 m。如图1 所示，研究深440 ～636 m 段的C70 混凝土井筒内壁，其厚度为1.2 m，可视为大体积混凝土，外壁厚度为0.5 m，内、外壁间铺设约3 mm 的双层塑料板。内壁向上部浇筑平均速度近似为6～8 m/d，在浇筑后12 h 内即拆模受荷。

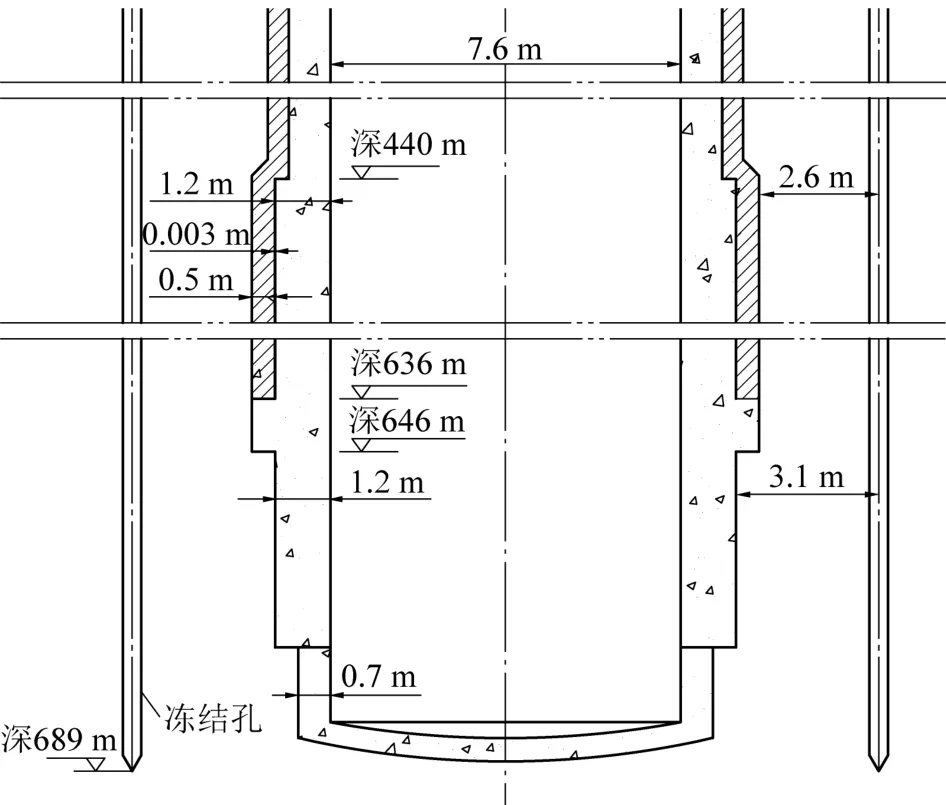
图1 井壁结构与冻结孔剖面Fig.1 Section of shaft wall structure and arrangement of freezing holes

2 深部冻结井筒内壁热-力耦合数值模型

2.1 基本假设

深井冻结井筒内壁早期温度应力问题是非常复杂的热-力耦合计算问题，对涉及的物理量进行如下假设：①内层井壁、外层井壁及冻结基岩为线弹性材料；②假定土层中的水全部结冰，即不考虑冻土中存在的未冻水，且不考虑井壁混凝土中的水分；③螺纹钢筋与井壁混凝土之间的围抱力足以促使井壁温度变化过程中钢筋和混凝土协调变形；④固态力学计算中，内、外壁间塑料板摩擦因数近似聚乙烯塑料板，取0.27；⑤混凝土外壁与冻结基岩粘结紧密，基本无滑移；⑥深440～636 m 内壁浇筑30 d 内冻结壁仍未融化，不考虑水荷载作用；⑦浇筑内层井壁混凝土之前，冻结管周围已经形成设计厚度的冻结壁，将冻结管简化为恒温冷源。 ⑧井筒为圆形结构，井壁温度、应力等载荷和约束均基本以井筒直径为轴对称，故热-力耦合模型可按照空间轴对称问题进行求解。

2.2 控制方程

根据固体热传导原理，冻结井筒内壁为均质各向同性轴对称模型，遵循导热方程：

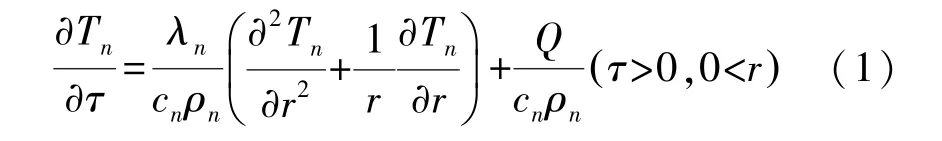
式中：Tn为井壁温度，℃；n为介质类型，n＝1 为内壁混凝土，n＝2 为外壁混凝土，n＝3 为冻土；τ为冻结时间，d；λn为导热系数，W/（m·K）；cn为比热容，kJ/（kg·K）；ρn为密度，kg/m3；Q为单位时间内单位体积的混凝土水化放热量，kJ；r为内壁某点与内缘间距离，以井筒中心为原点，m。

根据弹性力学，平面应变的轴对称热应力的控制方程为

式中：σr、σθ、σz、τrθ分别为径向、换向、竖向、切向应力，MPa；D1、D2为待定系数；αf为内壁混凝土热膨胀系数；μ为内壁混凝土泊松比；E为内壁混凝土弹性模量，MPa；a为内壁内半径，m。

冻结井筒内壁内缘无荷载，则有边界条件

式中：σr( )r＝a、σr( )r＝b分别为内壁内缘、外缘的径向应力；b为内壁外半径，m；P1为外缘受到外壁与冻结壁共同作用的侧压力，MPa。

将式（3）代入（2），解得：

2.3 参数选取与边界条件

数值模型以深620 m 层位内壁混凝土浇筑为研究对象。考虑到井筒掘砌荒径、冻结壁厚度、掘砌段高等尺寸，求解域径向长×轴向高＝4 300 mm×5 000 mm。分别包括：内壁厚度1 200 mm，外壁厚度500 mm 和冻结管至外壁距离2 600 mm。采用四边形网格划分，数量为8 600 个。根据不同阶段，热物理参数与边界条件如下。

1）内壁浇筑前阶段。土体初始温度设置为26℃。在内壁浇筑前，外壁井帮温度实测在0 ℃左右。故在内壁浇筑前，应当进行瞬态温度场分析，冻结管简化为-20 ℃恒温冷源持续供冷，直至外壁内侧井帮温度达到0 ℃视为内壁浇筑起始温度边界条件。温度场数值计算涉及各个材料热物理参数均由室内试验获得，见表1。

表1 热物理参数Table 1 Thermophysical parameters

2）内壁浇筑0～10 d。内、外壁间厚3 mm 双层塑料板可简化为接触传热模型［18］，则有

式中：q为单位温度单层塑料板单位面积的传热量，W/m2；λs为塑料板导热系数，取0.15 W/（m·℃）；δs为塑料板厚度，m；ro为内壁外半径，m；Δt1为塑料板两侧温差，℃。

内壁砌筑施工时井筒内自然对流换热过程是空气与井筒内表面换热问题。研究表明混凝土表面换热系数与风速、空气和井壁内表面温差2 个因素符合如下关系［19］：

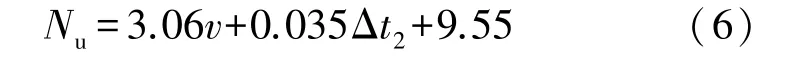
式中：Nu为内壁混凝土表面换热系数，kJ/（m2·h·℃）；v为井筒内风速，m/s，根据井口实测取2 m/s；Δt2为空气与井壁内表面温差，℃。

内壁混凝土水化热采用目前国内常见的水化放热数学表达式［20］，包括：指数式、双曲线式和复合指数式分别见式（7）—式（9）。寻找与C70 内壁混凝土水化放热误差最小的模型：

式中：Qi（τ1）为在龄期τ1时累积的水化热，kJ/kg；i为不同水化放热模型，i＝1 为指数式，i＝2 为双曲线式，i＝3 为复合指数式；Q0为龄期τ1趋于无穷大时的水化热， kJ/kg，采用 P. O 525 水泥故取350 kJ/kg；m为常数，与水泥品种、比表面积及混凝土浇筑温度有关，取0.362；n1为水化热达到1/2 时的龄期，取0.2；α、β为待定参数，分别选取0.36 和0.74。

内壁混凝土绝热温升计算公式为［20］

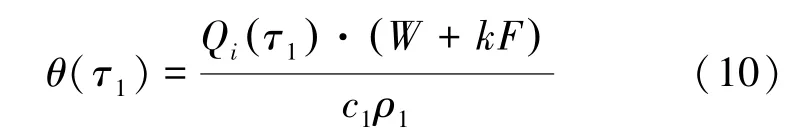
式中：θ（τ1）为内壁混凝土不同龄期的温度，℃；W为每立方米混凝土胶凝材料用量，kg/m3；F为单位体积混凝土混合材用量，kg/m3；k为折减系数，粉煤灰折减系数为0.25。

利用式（2）—式（4）进行温度场-应力场直接耦合。所需力学参数包括：弹性模量、泊松比、内壁上表面和外表面荷载、热膨胀系数等。

朱伯芳院士等［20］认为混凝土的弹性模量是随着时间而变化的光滑连续函数，利用指数函数式进行拟合，则有

式中：E τ1( ) 为不同龄期的弹性模量，MPa；E0为混凝土最终弹性模量，MPa；α2、β2为待定系数，根据弹性模量实验结果分别选取0.09 和1。

根据DL/T 5150、SL352《水工混凝土试验规程》规定［21］，假设混凝土的温度与变形呈线性关系，混凝土的热膨胀系数为某一常数，取1×10-5℃-1。应力场数值计算涉及材料物理力学参数均由室内试验获得，见表2。

表2 井壁物理力学参数Table 2 Thermophysical parameters of shaft

内层井壁上表面荷载计算公式为

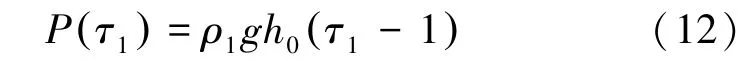
式中：P τ1( ) 为不同龄期井筒内壁上表面荷载，MPa；g为重力加速度，取9.8 m/s2；h0为1 d 内浇筑高度，取8 m。内壁外表面（外缘）荷载包括内外壁间摩擦力和水平应力。内外壁间摩擦力在接触对模块中进行模拟，选择增广拉格朗日法进行求解。根据现场监测在内壁浇筑期间该层位外壁受到水平应力为2.2 MPa。

3 冻结井筒内壁早期温度场演化特征

3.1 水化热温升模型确定

如图2 所示，龄期1 ～2 d，井壁中线点温度最高，两者分别为68.84、69.19 ℃，实测值与数值模拟结果误差为0.5%。其原因为实际施工浇筑过程中，现场诸多因素都会影响混凝土的温度变化。可见，数值计算过程中的热物理参数、边界条件、初始条件的选取都是合理可靠的。相同参数条件下采用复合指数式水化热温升模型计算出结果与监测点温度更接近，表明复合指数式较其他2 种水化热温升模型更适用于计算深井内壁早期水化热计算。

图2 不同时刻内壁中心位置温度历程Fig.2 Temperature history in center of inner wall at different time

3.2 早期温度场演化特征

在龄期240 h 范围内，井筒内壁混凝土中心位置的最高温度出现在15 h 左右（图3）。该时刻内壁温度一直呈中部温度高，内外缘温度低的分布规律。其原因为井筒内壁大体积混凝土水化放热剧烈，且井壁中心混凝土热传导能力较差，靠近内壁内缘（靠近模板侧）的井筒风流与靠近外缘（靠近外壁位置）的冻结冷源均基本不能够影响中心位置混凝土温度，而井壁内外缘均产生降温现象。在水化放热阶段，大量的水化热会导致内壁混凝土中部温度短期内（0 ～48 h）急剧上升至70 ℃左右，而该时刻靠近外壁侧井壁温度为38 ℃左右，靠近井筒内部的温度为58 ℃左右。可见大体积混凝土内外温差已经超过规范限制的25 ℃，极易导致温度裂缝的出现。内壁混凝土水化放热中后期（120 ～240 h），内壁混凝土中部到内缘温度较高，外缘温度低。

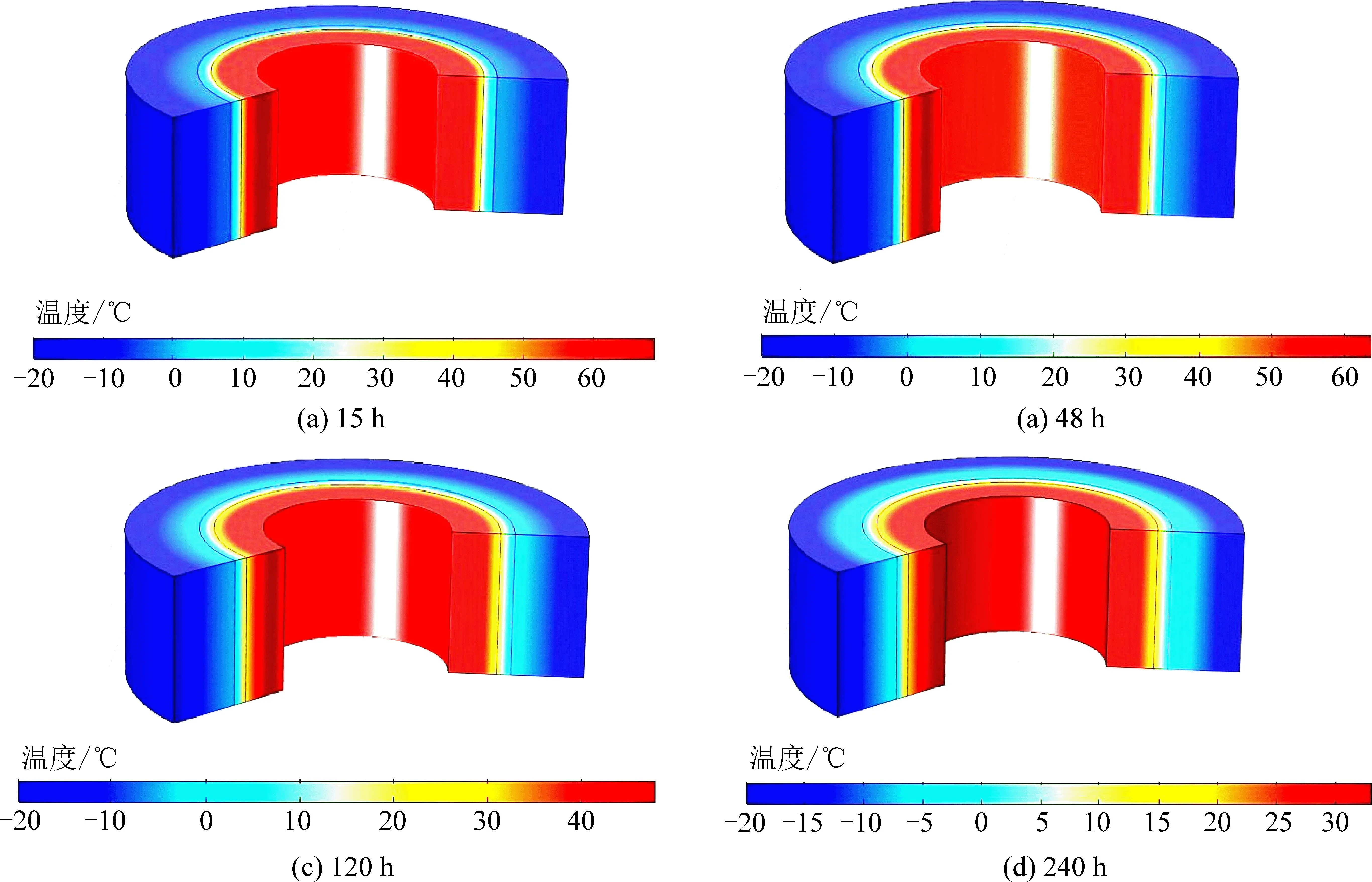
图3 不同龄期内壁温度场Fig.3 Temperature field of inner wall at different time

4 冻结井筒内壁早期应力场演化特征

4.1 数值计算与现场实测应变对比

红庆河煤矿混凝土环向应变计位于内壁内缘侧，数值模拟获得不同龄期内壁内缘应变与深615 m 位置井筒内壁内缘混凝土竖向应变曲线变化趋势基本一致（图4）。二者均在内壁早期水化放热时期应变急剧增大，该时期内壁内侧的混凝土产生较大的膨胀变形，由于约束程度较小，应变最大值达到6.5×10-4～7.0×10-4，误差为7.52%，满足工程精度。可见，数值计算过程中的物理力学参数、边界条件、初始条件的选取都是合理可靠的。

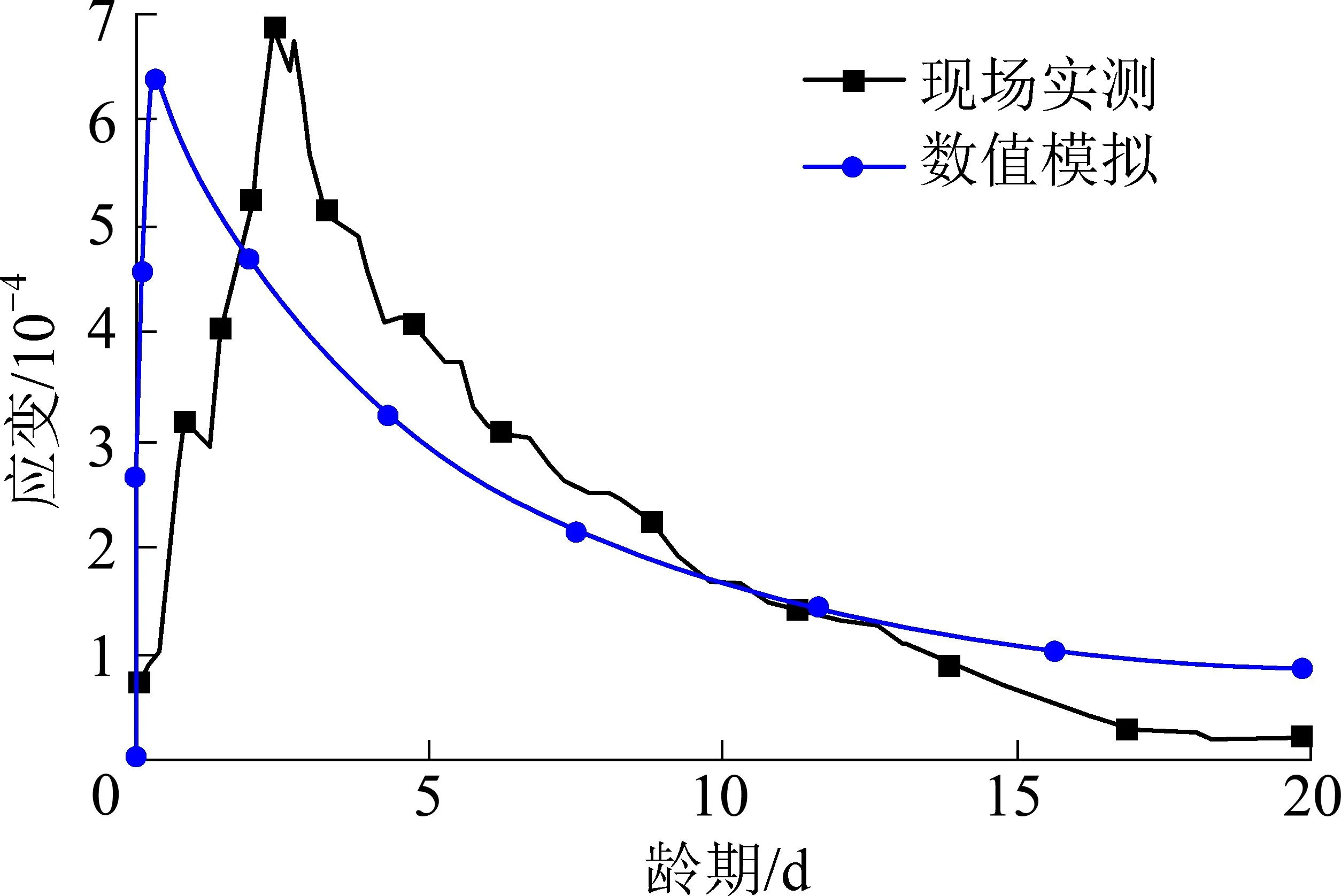
图4 内壁内缘应变模拟结果与实测结果对比Fig.4 Comparation of strain between numerical simulation and field test in inside of inner wall

4.2 早期应变场演化特征

内壁混凝土浇筑24 ～48 h 时，内壁各位置应变为正，且呈内缘至中部大于外缘的规律（图5）。其原因为混凝土水化放热导致内壁内会产生较大的膨胀变形，且膨胀应变量与井壁温度呈正比关系，符合混凝土水化放热膨胀理论。随着内壁温度的不断下降，膨胀变形缓慢减小，至120 h 最大膨胀应变下降至4×10-4。当内壁混凝土浇筑240 h 后，内壁外缘至中心区域出现收缩变形，最大为-6×10-5。而此时内壁内缘至中心区仍然保持膨胀变形，最大变形为2.5×10-4。表明由于外部冻土持续供冷导致内壁出现不均匀变形现象，内壁外缘产生收缩变形早于中心与内缘部分，造成内壁外缘在浇筑后240 h 内就受到竖向拉应力作用，较容易在该区域内最先产生温度裂缝。

4.3 早期应力场演化特征

在内壁浇筑初期（24 ～48 h），随着内壁混凝土温度逐渐升高，混凝土会发生膨胀变形，在水平荷载、外壁摩擦力与上部连续浇筑内壁混凝土重力共同约束下内壁内部逐渐形成了一定压应力，其分布规律为内壁中部压应力大于内外缘（图6）。随着内壁温度的不断下降，混凝土逐渐产生收缩变形。至龄期为120 h 时，内壁内外缘储存的预压应力逐渐减小趋于0，而此时内壁中心部位仍然存在约为-2 MPa的压应力区。当龄期为240 h 后，在内壁外缘附近出现明显的拉应力，达到1.5 MPa 以上。而此时内壁中部至内缘区域仍然储存-1 MPa 左右的压应力。综上所述，深井内壁混凝土早期应力场分布不均匀，大体为浇筑初期内壁压应力由外缘至内缘先增大后减小，浇筑后期内壁外缘受拉，内壁中部至内缘受压的演化规律。

图5 不同龄期内壁应变场Fig.5 Strain field of inner wall at different time

图6 不同龄期内壁应力场Fig.6 Stress field of inner wall at different time

内壁内缘至中部范围内（0～0.6 m）混凝土的压应力在龄期0 ～480 h 的变化较小，维持在-0.5 ～-1.0 MPa，如图7 所示。表明该区域混凝土在膨胀与收缩过程中受到外荷载约束较小，不会出现由于早期温度应力导致的损伤或裂缝。内壁中部至外缘范围内（0.6～1.2 m）随着龄期增长逐渐由压应力变为拉应力，拉应力最大值处为内壁外缘位置。其原因为混凝土在收缩期间受到上部及水平荷载、塑料板摩擦力等边界条件的约束，内壁竖向受拉。当龄期为480 h 时，内壁外缘拉应力达到2.2 MPa，与C70 混凝土抗拉强度接近。表明内壁混凝土早期温度应力形成的裂隙（缝）将首先出现于内壁与外壁交界位置，当冻结壁化冻后高压水进入内壁周围将不断腐蚀裂缝尖端，且高压作用下裂缝不断扩张，直至形成贯穿裂缝，最终造成井壁破裂、渗水甚至透水等现象。

随着井筒深度不断增加，内壁混凝土强度等级逐渐增加，水化放热量相应提高。导致内外壁温差增大，早期温度应力引起的井壁早期温度裂缝的风险增加。通过数值分析结果可知，混凝土早期温度裂缝防治措施优化方向应当包括：优化塑料板材料，减小内外壁间摩擦力；优化混凝土配合比，降低内壁混凝土水化放热；提高内壁混凝土预压应力，减小收缩变形量；提高内壁混凝土抗拉强度与抗裂性能，降低开裂风险；多次进行壁间注浆，及时封堵内壁外缘可能形成的裂隙（裂缝）区域［22］；优化井壁结构，增加混凝土内部降温结构以减小温差等［23］。