信号时序逻辑约束下基于终点回溯的高效规划

田戴荧，方 浩，杨庆凯

（北京理工大学自动化学院，北京 100081）

1 引 言

近年来，时序逻辑理论作为计算机领域中用来进行正则化检验的一套方法[1]，被应用于机器人规划与控制中，取得了极大的应用成果。时序逻辑理论的主要思想是将时序逻辑任务约束转换为可以处理的约束形式，从而在规划时考虑这些约束，生成满足任务的路径。其中，线性时序逻辑（Linear Temporal Logic, LTL）将时序逻辑约束转换为Buchi˙˙ 自动机[2]，而对于信号时序逻辑（Signal Temporal Logic, STL），由于其处理的主要是连续系统，不能找到一个合适的图来作为其约束集。

针对连续系统中信号时序逻辑的控制方法，近年来有越来越多的学者进行了研究。伯克利大学的Raman 等人[3]将信号时序逻辑编码为离散值的组合作为整数约束，之后结合模型预测控制，将信号时序逻辑约束下的规划问题建模为混合整数线性规划问题。Bapinar 等人[4]将混合整数线性规划方法用到了多无人机系统的规划与控制中。Farahani 等人[5]在混合整数线性规划方法的基础上，针对自动系统所处的不确定性环境研究了控制的鲁棒性问题，对最坏情况下的模型预测控制问题进行了求解，从而得到了一个反应式的控制器。舒新峰等人[6]提出了一种命题投影时序逻辑的分布式模型检测方法，缓解模型检测的状态空间爆炸问题。此外，为了给STL 约束构建一个光滑的约束函数，Haghighi 等人[7]提出了一种新的光滑可微STL 量化语义来累积鲁棒性，并通过策略上升方法求解一系列光滑优化问题有效地计算控制策略。Lars 等人对此提供了一种新的视角，他们首先定义了控制屏障函数与信号时序逻辑进行结合，同时，考虑时变控制屏障函数，其中时间特性用于满足信号时序逻辑任务。该控制器由计算效率高的凸二次规划和局部反馈控制律给出[8]。同时，基于三维时空的规划方法[9]也有了较多研究。这些方法可以与传统控制方法有很好的结合，比如将混合规划得到的结果输入到具有非线性前馈补偿与闭环反馈控制系统[10]中，或者基于航路点分段的预测校正方法[11]中，作为额外知识指导校正。这些方法可作为无人机的避障航路规划算法[12]，引导无人机生成满足任务约束的路径。

除控制视角之外，有大量学者尝试从学习的角度出发，对信号时序逻辑约束的规划问题进行有效求解。其中Aksaray 等人[13]针对STL 的健壮性不是Q-learning 标准回报形式这一问题，对STL健壮性指标用标准回报形式的函数进行了近似，从而能够利用标准强化学习生成满足STL 约束的路径。Balakrishnan 等人[14]进一步设计了每一个局部状态局部任务的回报奖励，并且将局部状态组合后能够满足整体STL 任务的约束。除了Q-learning 之外，考虑到STL 的正确性是以与子公式数量和时间约束数量呈指数的计算复杂量来保证的，Kurtz 等人[15]提出了一种替代的求解方法，这种新的求解方法依赖于贝叶斯优化而不是混合整数线性规划。贝叶斯优化放宽了满足STL任务的概率完备性，即路径在一定概率范围内可能违反任务，但是求解效率大幅提高。此外，考虑利用STL 任务具有特定模式，其中的一部分规划结果可以作为知识指导其他任务的路径生成，Li 等人[16]提出了一种新的基于图的时空逻辑，通过将Hilbert 公理化应用于基于图的时空逻辑，采用Modus ponens 和IRR 作为推理规则最终实现了一套完备的逻辑推理框架，可以用于知识表示和自动推理。从STL 自身具有时间约束的特性出发，Varnai 等人[17]针对具有部分已知动力学的系统，提出了一种基于抽样的学习方法来解决包含任务满足约束的最优控制问题。用STL 构建动态辅助任务，引入了一个控制器衍生框架，从而能够对学习进行高效率的指导。有了高效率的控制器，STL 语言完全可以应用于复杂系统，比如多机器人的规划问题[18-20]中。

以上提及的方法中，基于控制的方法在线规划时具有极高的计算复杂度，基于学习的方法收敛时间长，且得到的路径重用性差，当起点或者目标点发生改变时，需要重新进行学习以生成最优路径。针对这些问题，本文提出一种基于终点回溯的高效规划方法。注意到未来操作符以及过去操作符的对应顺序，将所有未来（过去）操作符转换为对应的过去（未来）操作符，对所有转换后的操作符构建对应的Transducer[21]。在离线构建阶段，在机器人的工作环境中加入时间维信息，构建时空联合空间，在该联合空间中，提前指定满足任务的合理终点，在Transducer 的指导下，以终点作为快速随机搜索树的起点[22]，回溯至初始状态平面。当采样点足够多时，每一个初始状态都能够在快速随机搜索树中寻找到一条时间反序序列满足任务约束。在线规划阶段，每一个状态根据快速随机搜索树生成完成任务代价最小的时间反序序列，之后利用模型预测控制进行跟踪。

2 信号时序逻辑指导的离线构建

信号时序逻辑是一类形式化语言，能够表述时间与逻辑上的约束关系。其在机器人规划领域的应用价值在于其能够提供高阶任务的表述方法，来控制机器人完成一系列具有先后顺序关系的动作，比如，先打开门才能进入房间，以及机器人每30 分钟要前去充电。STL 的具体语法定义为

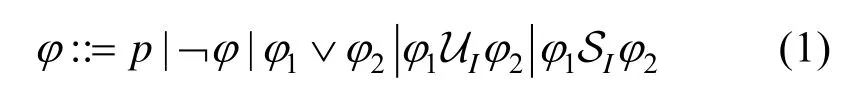
其中，I=[a,b]为一时间区域；p为原子命题，通常为环境的标签或者机器人的某一个动作；¬φ是对φ取反；为φ1或是未来形式，指在φ1为假之后的I时刻内，φ2需要为真；φ1SIφ2是上式的过去形式，指在φ2成真之后的I时刻内φ1需要为真。各公式的形式化定义如下，其中w为一带有时间的序列。

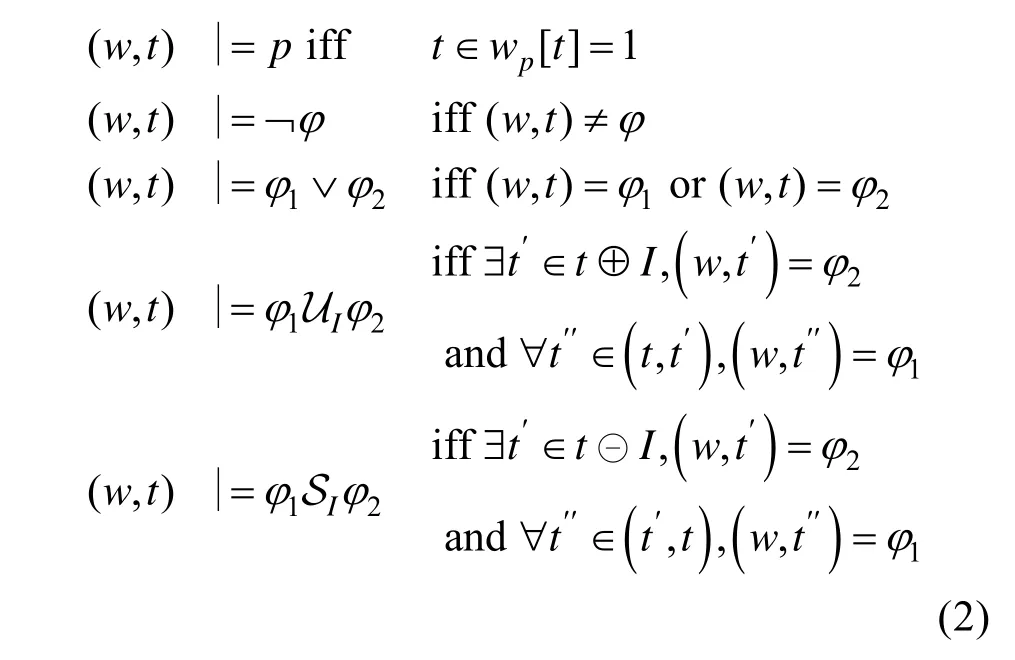
此外，F（Eventually）、G（Always）以及它们对应的过去形式可以定义如式(3)。

Thomas 等人[21]已经说明，所有STL 公式均可以通过F、F、UI以及SI构造得到，因此之后以这几个公式为例子。

定义h为判断每一个公式是否为真的最小时间间隔，其定义如式(4)：

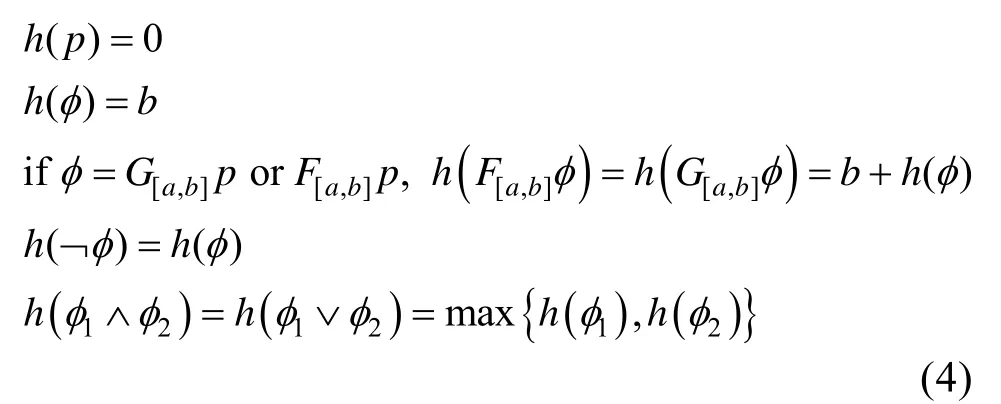
对于STL 公式，存在度量一条路径w对于公式的满足程度的公制单位，称为鲁棒程度，r：w×φ→ℝ。r采用迭代形式进行计算，如式(5)所示。

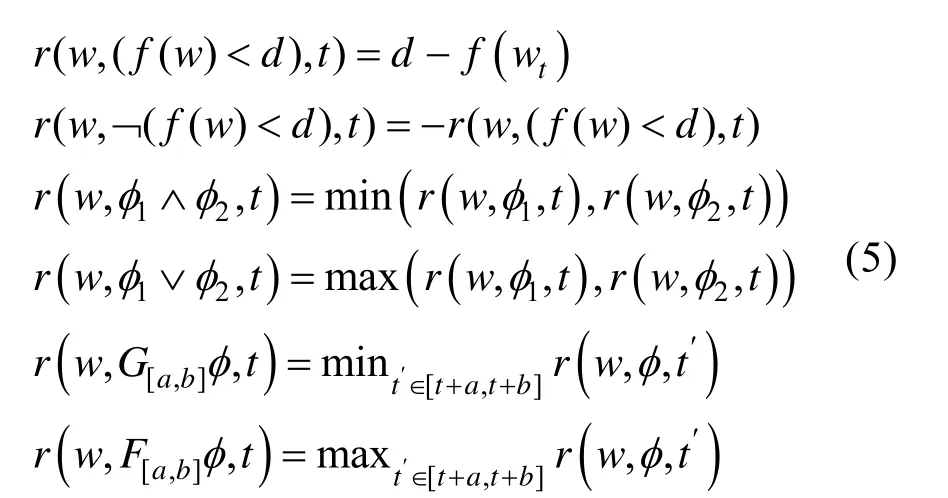
每一个 STL 的时序逻辑符都有一个Transducer 与之对应，如图1 所示。对于任意一个任务，可以将其所有的时序逻辑符的Transducer 按照公式树的顺序组合起来，便能够形成整个公式的Transducer。

定义 1.对于任意一个带有时间的序列，其时间反序序列定义为

定理1.对于任何一个任务，若存在一个序列满足未来（过去）形式任务，则此序列的时间反序序列满足该任务对应的过去（未来）形式。

图1 (a)为 F(0,b)对应的Transducer，(b)为 U(0,∞) 对应的Transducer，(c)为φ：=G(0,∞) F[0,5)¬p1 (p2U[0,10] p3G(0,15) p4)对应的语法树Fig.1 (a), (b) are the transducer of F(0,b)and U(0,∞),respectively.(c) is the parse tree of φ：=G(0,∞) F[0,5)¬p1 (p2U[0,10] p3G(0,15) p4)

证.证明仅以 UI以及 SI为例，其他对应公式证明方法类似。假设w =( s0, t0)( s1, t1)...( sn, tn∣)= a UIb，则根据公式（2），有

则在构建时间反序序列时，有

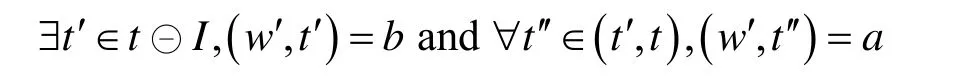
这恰好符合a SIb的定义，因此如果w∣= aUIb，则有 w∣'= a SIb。

在机器人工作的( x,y)空间中，加入时间维信息，构建(x , y,t ) 三维空间，并根据机器人被指定的任务预估其终点，则在t h= 的平面上提前放置终点，表示为sd=( xd, yd, h)。将该点作为根节点。同时，将给定任务的所有未来（过去）操作符转换为过去（未来）操作符，并构建转换后任务 φn的Transducer，表示为TSn。在TSn的指导下，自sd向t= 0的平面生长快速随机搜索树。根据定理1，快速随机搜索树生长的所有满足转换后任务φn的时间反序序列，在正向执行时一定满足原任务要求。

将所有采样点的集合表示为S，所有完成任务的采样点的集合表示为 S ',对于每一个采样点sa ∈ S，根据其与终点距离给定一个代价值，同时，将对STL 任务的符合程度乘以偏好因子加入到代价值中，定义如式(6)。

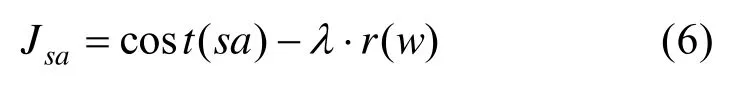
在构建完搜索树之后，树上的每一个节点都有对应的一个代价值，表征着从这个节点开始到达终点的路径的整体代价。

3 在线规划

当定理1 采样到足够多的数据点之后，离线构建搜索树结束，此时所有满足任务 φn的叶子节点前往根节点的路径在正向执行时一定满足原任务。在这些叶子节点足够多时，初始状态平面的每个有可能完成任务的状态点就将被覆盖到。考虑一个以完成任务的叶子节点为顶点，最大速度作为斜面斜率绝对值的圆锥（如图2 所示），则圆锥中所有状态点都可以通过导航至圆锥顶点，并由顶点到随机搜索树根节点连接一条后续路径来生成满足任务约束的路径。

在任意给定一个初始状态之后，机器人将在所有的满足任务叶子节点L 中选择代价值 Jsa最小的那个叶子节点，从叶子节点到根节点依次连接，能够生成一条满足任务的时间序列w。在w中以一定时间分辨率进行点的采样，便可以构成一条由带有时间的路径点构成的路径pa。本文中采用模型预测控制对pa 进行跟踪，具体问题建模如式(7)。

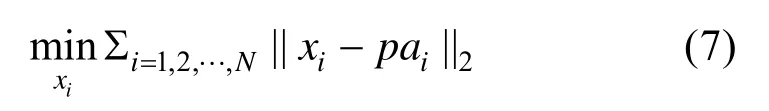
该式可以根据不同的系统进行不同的定义，并可以额外加入其他的约束条件，比如加入控制屏障函数的约束以保证任意分辨率内路径都会满足任务约束。在本文中，由模型预测控制生成的最优控制量可以储存至对应的节点中，当又一次规划至该节点，且控制对象的状态与该点预置状态相近时，可以直接应用之前预置好的控制量进行控制，进一步减少在线运算时间。至此，离线构建以及在线规划阶段的算法都已完成，本文算法整体框架如图3 所示。

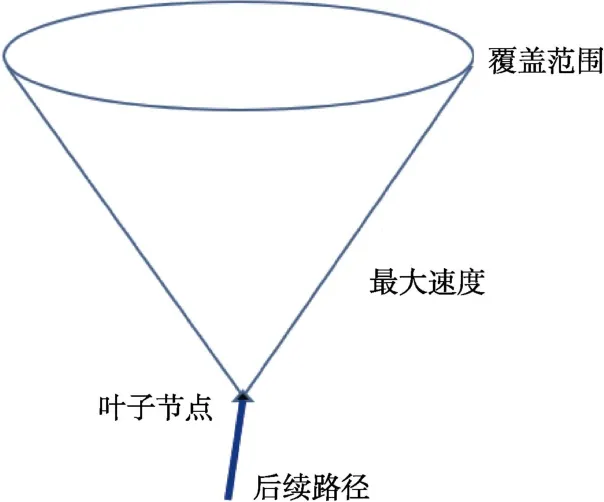
图2 节点的覆盖范围圆锥Fig.2 Cone representing cover region of leaf nodes

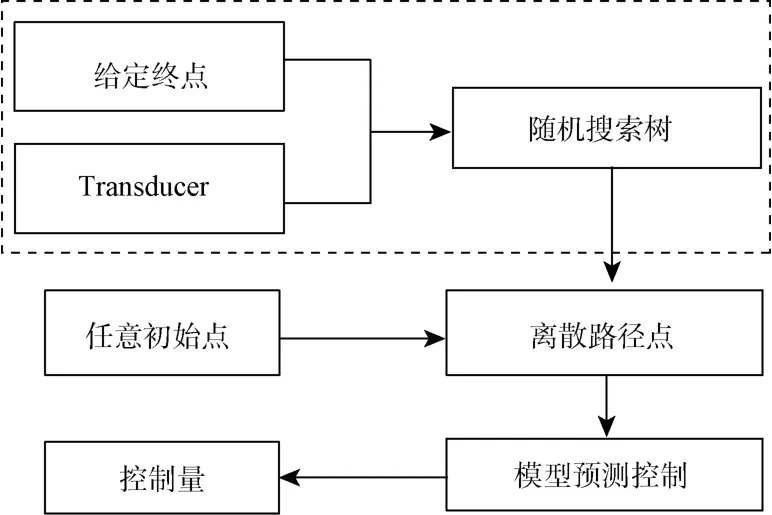
图3 算法整体框架Fig.3 Framework of algorithm

4 仿真结果及分析

对于算法的结果，在内核为i5-7300HQ 的计算机上基于Python3 构建了仿真程序，进行了仿真实验。

实验中指定给机器人的任务表述为，在实验开始后的0s 到10s 内，到达a区域，在到达a区域的10s 到18s 内，到达b区域。STL 公式为实验的具体环境如图 4所示。其中，标为“obs”的蓝色圆圈代表障碍物，a区域和b区域均为黄色圆圈。

离线构建阶段生长出的随机搜索树如图5 所示。在构建好随机搜索树之后，在线规划阶段任意给定初始状态点，可以立即生成离散路径，三维离散路径如图6 所示。对该路径每隔一定时间间隔进行采样，便可以生成一系列路径点。

本文考虑两轮差速小车模型。其模型描述如式(8)。

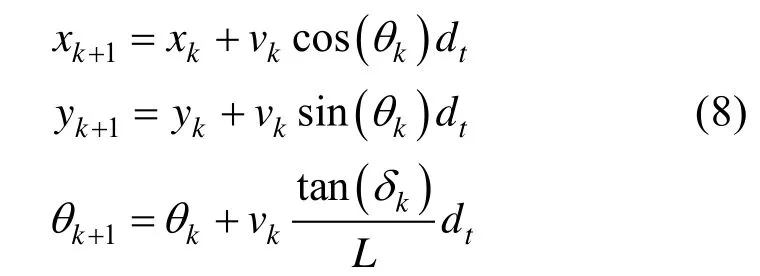
图4 仿真环境Fig.4 Simulation environment

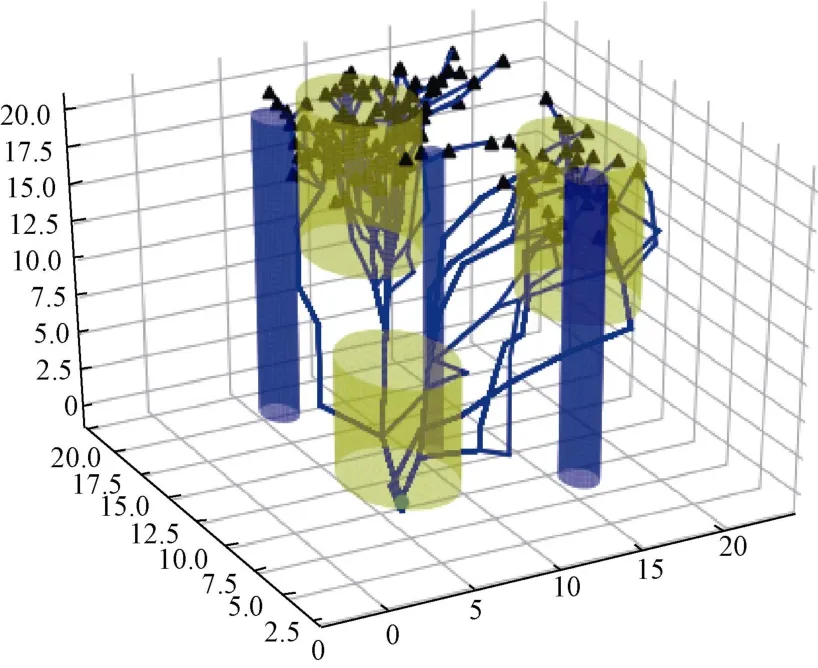
图5 快速随机搜索树Fig.5 Rapidly-exploring randomized tree

针对该动力学模型，采用模型预测控制解决式(7)问题，所得出结果如图7 所示。图7 中蓝色三角形为本次规划各个离散化时间点处车辆的位置，红色三角形为上一次规划时预置的控制量。当蓝色三角形与红色三角形基本重叠时，直接采用预置控制量进行控制，不再进行模型预测控制。

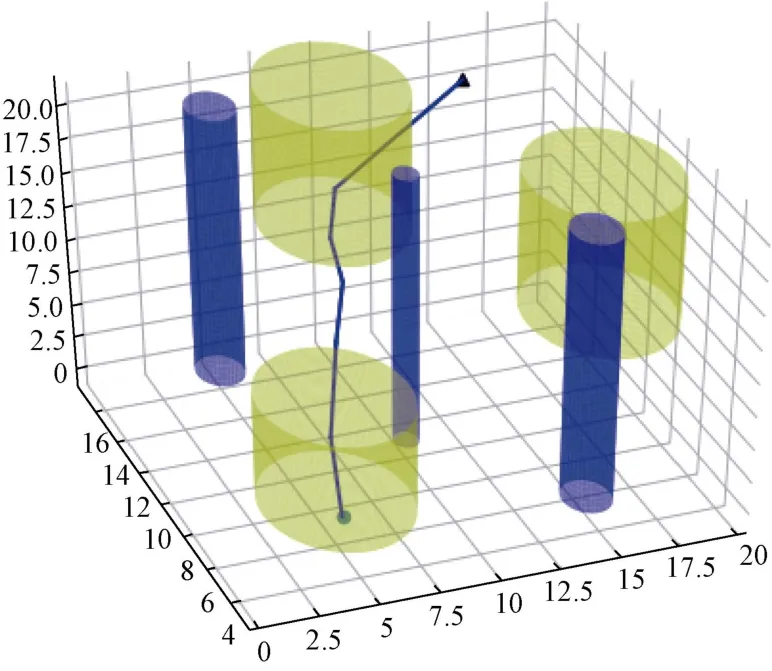
图6 三维规划路径Fig.6 Planning path in 3-D view

图7 最终控制效果 Fig.7 Final control effect

为了进行对比，实现了混合整数线性规划以及贝叶斯优化方法。混合整数线性规划生成最终路径耗时108.6 s，贝叶斯优化方法使用了17.9 s 在线规划生成了在一定概率下满足任务的路径。本文提出的方法在离线为所有初始状态点构建路径时，采样了5000 个点，耗时68.3 s，在线规划寻找相关路径耗时0.2 s，生成控制量耗时2.3 s，且在成功匹配到预置状态之后，不再需要在线计算控制量。

5 结 论

本文针对连续空间内在STL 约束下进行路径规划时间复杂度高，且规划的结果不易重用的问题，将问题放到带有时间信息的三维空间中进行求解，根据STL 未来时序操作符号与过去时序操作符的对应关系，利用由终点反溯的随机搜索树覆盖初始状态平面，之后在在线规划阶段寻找代价最小的点，采用模型预测控制跟踪该代价最小路径。通过对这一过程进行仿真，证实了本方法的可行性，且通过与混合整数线性规划以及贝叶斯优化方法进行对比，本文所提出方法能够在较短时间内有效求得所有初始状态符合任务约束的可行解。