基于松弛序列凸优化的轮式机器人协同轨迹规划
2021-04-17邓云山夏元清孙中奇
邓云山,夏元清,孙中奇
(北京理工大学自动化学院,北京 100081)
1 引 言
随着移动机器人技术的发展以及通信技术、计算机小型化技术的日益成熟,将一个复杂的任务分配给多个结构、功能都相对简单的智能体来完成已经成为一个热门的研究方向[1],其中协同规划技术是多智能体协同技术中的重要组成部分。多智能体协同轨迹从建模方式上分为两类[2],第一类为基于简单的转弯半径与避碰约束的搜索方法,如图搜索方法[3]、树搜索方法[4]、人工势场法[5]等。这些搜索方法将模型约束进行了抽象化处理,提炼成简单的几何约束,从而进行搜索,具有规划效率高、计算需求低的特点,但缺点是未考虑完整的模型约束,规划轨迹可能在实际中不可行。第二类为基于优化理论的方法,将轨迹规划问题建模为优化问题,求解方法主要包含伪谱法[6]、混合整数规划方法[7]、智能优化算法[8]等。
随着凸优化理论的发展,内点法可在多项式时间内对二阶锥优化问题进行有效求解[9-10]。国内外众多学者利用凸优化技术针对不同对象进行了协同轨迹规划问题的求解。文献[11]利用序列凸优化方法求解了航天器集群变轨问题,并给出了分布式策略架构;文献[12]以最优时间为代价,利用凸优化方法求解了无人机协同轨迹规划问题,可实现无人机在时间上的协同;文献[13]采用滚动时域架构,将无人机协同轨迹规划问题转化为二次规划问题,在一定程度上增加了求解效率,并进行了室内飞行实验验证。同时,凸优化方法还用于星球软着陆[14]、再入飞行器轨迹规划[15]等工程问题。
针对地面机器人的轨迹生成问题,通常采用第一类搜索方法,将路径与速度进行分解,用样条插值等方法生成曲线路径[16],但面对协同轨迹规划中的复杂约束,第一类搜索方法规划轨迹的可行性有局限。而第二类方法通常没有考虑优化问题的凸化,直接使用非线性优化工具包进行求解,大大增加了协同轨迹生成问题的求解时间。对此,本文考虑具有非线性运动学方程的轮式机器人模型,考虑机器人物理性能约束、障碍规避约束、机器人避碰约束,建立多轮式机器人轨迹规划优化模型。通过凸化与离散化方法,将问题转化为序列二阶锥优化问题,同时对问题进行松弛处理,以提高问题可行性。最后,通过数值仿真,验证算法有效性。
2 问题描述
通过对轮式机器人运动学模型分析,得到单个轮式机器人的物理约束。建立多轮式机器人协同轨迹规划问题模型,含运动学方程、避障避碰约束、个体物理性能约束、终端约束及代价函数。
2.1 轮式机器人模型
轮式机器人是一个典型的具有非完整性约束的欠驱动系统[17-18]。全局坐标系下,其运动学方程可描述为
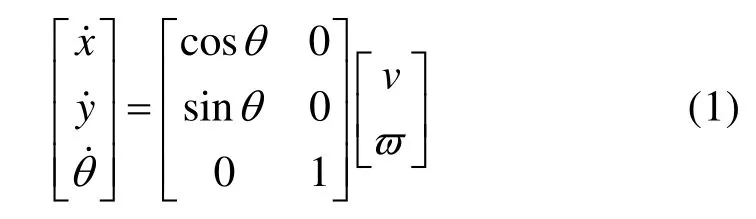
其中,[x,y]T为机器人在全局坐标系下的位置,θ∈( -π,π] 为速度方向与坐标轴X轴正向的夹角,v,ϖ为实际控制量,v为线速度,ϖ为角速度。
如图1 所示,vL与vR分别为左右轮驱动线速度,由于驱动电机机械特性,驱动速度大小有界,其中,maxv为单个轮子线速度上界。在无打滑假设下,线速度v,角速度ϖ与双轮线速度满足如下等式[19]:
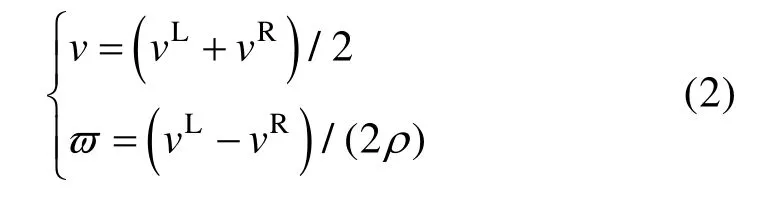

图1 轮式机器人模型示意图Fig.1 Model of wheeled robot
其中,ρ是左右轮间的半轴距。因此,单个轮式机器人需满足约束:
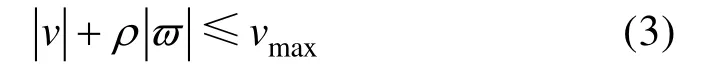
2.2 协同轨迹规划问题
多个轮式机器人在运动过程中,需要尽可能以较低能量抵达目标位置,同时在运动过程中,满足个体性能约束,规避障碍物以及其余个体。
为方便后续序列迭代中的线性化,将线速度也视为状态量, 则个体i的状态量为增加线速度导数a为控制量,则个体i控制量为从而运动学方程可写为
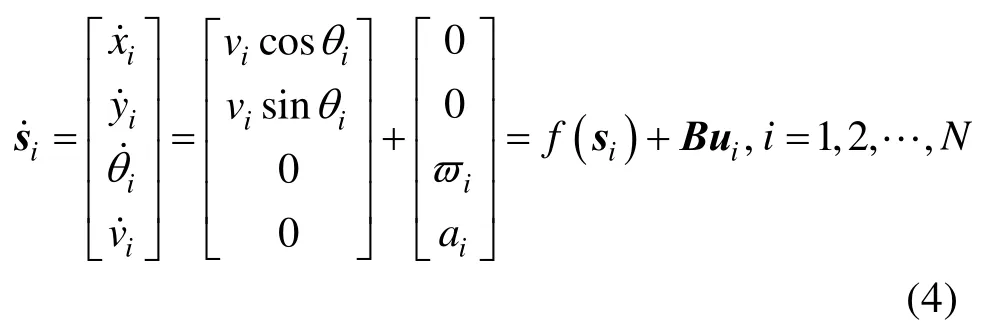
其中,N为机器人个数。
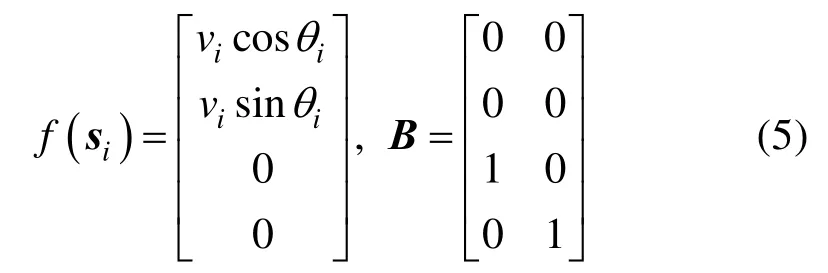
为保证机器人运动安全,各个机器人在任何时刻都应位于所有障碍区域之外,后续凸化中,圆形障碍较好处理,而实际运动中的障碍可被有限个圆形障碍覆盖,因此本文仅考虑圆形静态障碍。则障碍规避约束可表示为

同时多个机器人在运动过程中需要保证各个机器人相互避碰:

每个机器人需满足自身物理性能约束:

每个机器人的初始状态与终端状态给定,分别为
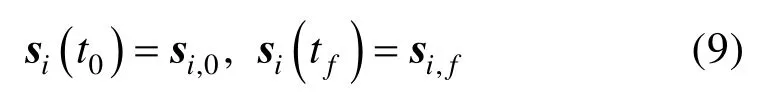
其中,t0为初始时刻,通常取t0= 0;tf为终端时刻,均为给定的已知量。 综上,以状态量与控制量加权二次型为性能指标,其中状态量二次型加权物理意义包含了任务本身的特殊需求;控制量二次型加权物理意义为能量最优需求。将多机器人协同轨迹规划问题建立为如下问题(P1):
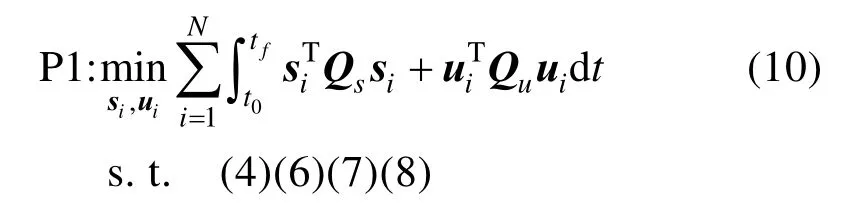
3 约束凸化
P1 包含非线性等式约束(4),非凸不等式约束(6)(7),是一个典型的非凸优化问题,由于现有的凸优化求解器要求目标函数和不等式约束函数均为凸函数,等式约束函数是仿射函数[2]。因此,建立P1 的凸化近似模型,同时将优化问题描述为多项式时间求解的二阶锥优化问题。
3.1 运动学模型线性化
将式(4)所示的非线性动力学在基准处线性化为
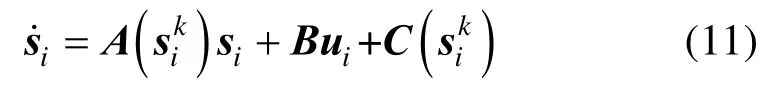
其中,

为确保线性化精度,增加信赖域约束

3.2 障碍规避约束凸化
将障碍规避约束(6)在基准轨迹处线性化,得到障碍规避约束的近似仿射不等式表达:

定理1:当si满足凸化障碍规避约束(14)时,必然满足原始障碍规避约束(6)。
证明:由于范数满足三角不等式,因此有
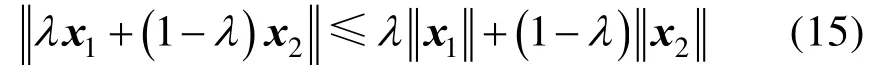

因此当凸化障碍规避约束(14)满足时,障碍规避约束(6)也满足。
3.3 机器人避碰约束凸化
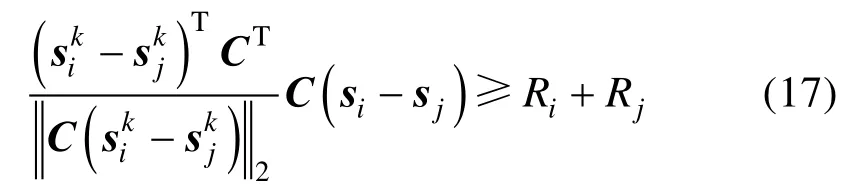
定理2:当满足凸化避碰约束(17)时,必然满足原始避碰约束(7)。
其证明与上述障碍规避证明类似,在此不做赘述。事实上,从几何意义上也可对障碍规避约束凸化与避碰约束凸化进行说明,如图2、图3所示。其中,

图2 障碍规避约束凸化示意图Fig.2 Obstacle avoidance constraint convexity
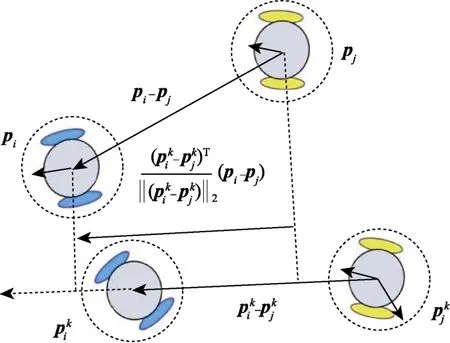
图3 机器人避碰约束凸化示意图Fig.3 Collision avoidance constraint convexity
凸化障碍规避约束(14)中,不等式左侧的第一项几何含义为机器人由基准位置指向当前位置的向量在由障碍物指向基准位置的向量上的投影,第二项几何含义为障碍物到基准位置的距离。整个不等式含义为,机器人需要在基准位置与障碍物连线上保持安全距离。如果机器人在基准位置与障碍物连线上保持了安全距离,则一定在二维空间上与障碍物保持了安全距离,即定理1 所述。
凸化避碰约束(17)中,不等式左侧几何含义为由机器人j当前位置指向机器人i当前位置向量在由机器人j基准位置指向机器人i基准位置向量上的投影。整个不等式几何含义为,任意两机器人需要在其基准位置连线上保持安全距离。如果两机器人在其基准位置连线上保持了安全距离,则在二维空间上,两机器人不会碰撞,即定理2 所述。
4 序列凸优化求解
本节将建立序列二阶锥优化子问题PP1k,进而求解原始多机器人协同轨迹规划问题P1。同时进行离散化,得到有限维二阶锥优化子问题PP2k。最后,为增加迭代过程中优化子问题的可行性,对某些约束进行松弛处理得到松弛子问题PP3k。
4.1 序列凸优化
序列凸优化将原始非凸优化问题转化为一系列可用现有求解器求解的凸优化子问题进行迭代求解,进而得到原始问题的近似解,图4 为序列凸优化(SCP)算法流程。记所有机器人状态为,控制量为。迭代求解步骤如下:
(1)初始化迭代次数k= 0,选择初始基准剖面
(2)迭代求解凸优化子问题PPk,得到解
(4)算法退出,获得原问题解。

图4 序列凸优化(SCP)算法流程图 Fig.4 SCP algorithm
结合第3 节中相关约束的处理,原始多机器人协同轨迹规划问题 P1 的序列凸优化子问题(PP1k)为

4.2 离散化
由于PP1k为无穷维问题,因此需要对时间进行离散化,将时间平均离散为n段,进而将无穷维优化问题转化为有限维优化问题。
将目标函数离散化为
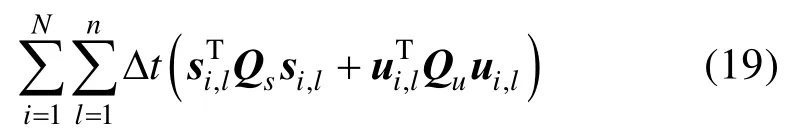
由于时间步长Δt为常数,因此可以忽略。
参考文献[20]状态方程离散方式,将机器人线性运动学方程(11)离散如下:
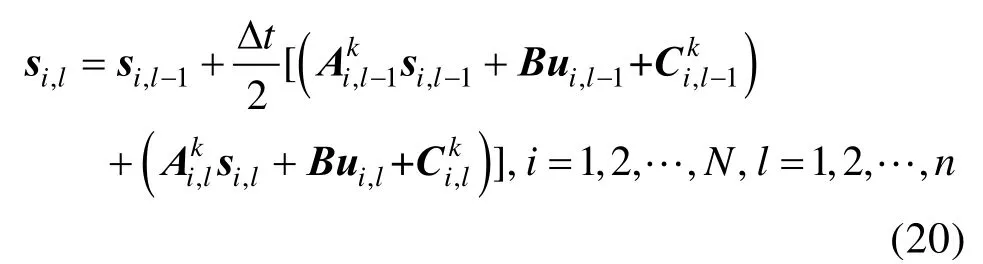
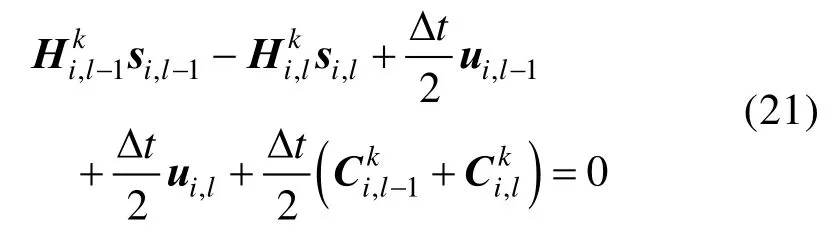
其中,

凸化障碍规避约束(14)离散化为

离散化后的障碍规避约束仅可保证在离散点处位于圆形障碍之外,无法保证两离散点间的障碍规避,因此增加约束(24),确保离散点间也满足障碍规避约束。

定理3[12]:当机器人i在各个离散时刻的状态满足约束(23)(24)时,其相邻两离散时刻位置的连线满足原始障碍规避约束。
证明:考察时刻tl,由于tl,tl-1时刻状态满足约束(24),而约束(24)为凸约束,因此任意连线上的点满足该凸约束(24)。由定理1 得,tl,tl–1时刻位置的连线上的点均满足初始障碍规避约束(6)。
利用数学归纳法可得,当各个离散时刻的状态满足约束(23)(24)时,相邻两离散时刻位置的连线也满足原始障碍规避约束。
凸化避碰约束(17)离散化为
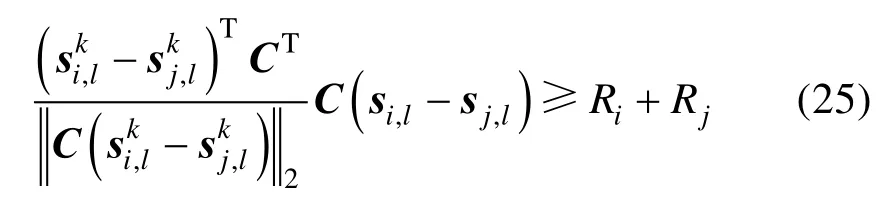
信赖域约束(13),物理性能约束(8),离散化后变为
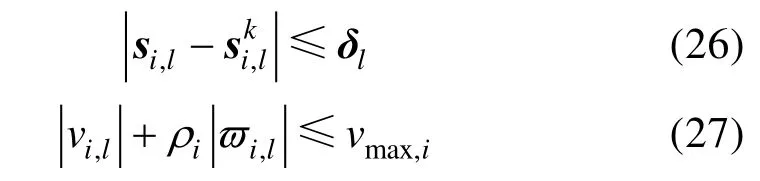
进而得到离散化后的凸优化子问题PP2k:

4.3 松弛化
为提高迭代过程中,凸优化子问题的可求解性,对约束(21)(23)(24)(25)进行松弛处理,松弛后的约束变为

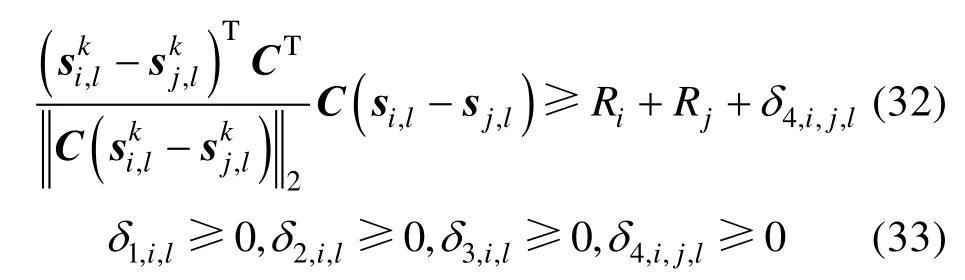
其中,δ1,i,l,δ2,i,l,δ3,i,l,δ4,i,j,l为松弛因子,需在约束中约束其大于0,在目标函数中增加惩罚项使约束尽可能满足,得到松弛后的凸优化子问题PP3k:

其中,α1,α2,α3,α4为松弛因子的惩罚因子,通常定义为足够大的正数。
5 仿真结果及分析
面向多轮式机器人协同轨迹规划问题,以障碍环境下的队形重构为例,开展数值仿真,仿真硬件环境为Intel Core i5-9400F 2.9GHz PC,编程环境为 Matlab 2019b,凸优化子问题采用YALMIP 进行问题建模,采用ECOS 求解器进行求解。最后进行不同规模轨迹规划仿真,与直接使用非线性最优控制工具包进行效率对比,非线性优化采用最优控制工具箱ICLOCS 进行问题建模,采用IPOPT 求解器进行求解。
障碍环境下的队形重构任务需要多机器人在给定时间从初始状态抵达目标状态,并且在过程中,保证机器人与圆形障碍的避撞及机器人之间的相互避碰。
以8 对轮式机器人N= 16为例,展示位置互换规划结果。轮式机器人左右轮间的半轴距ρ=0.0267 m ,单个轮子线速度上界vmax=0.13 m/s。一对机器人以状态1/2 分别为初始状态与目标状态进行队形重构,状态设置如表1 所示。
初始信赖域约束δ1的选择应恰好包括所有个体在执行任务时可能的状态,取值过大可能会降低求解效率。信赖域衰减是收敛性的保障,但衰减过快会导致求解失败,衰减过慢则增加求解时间,应选择适中的信赖域衰减方式。
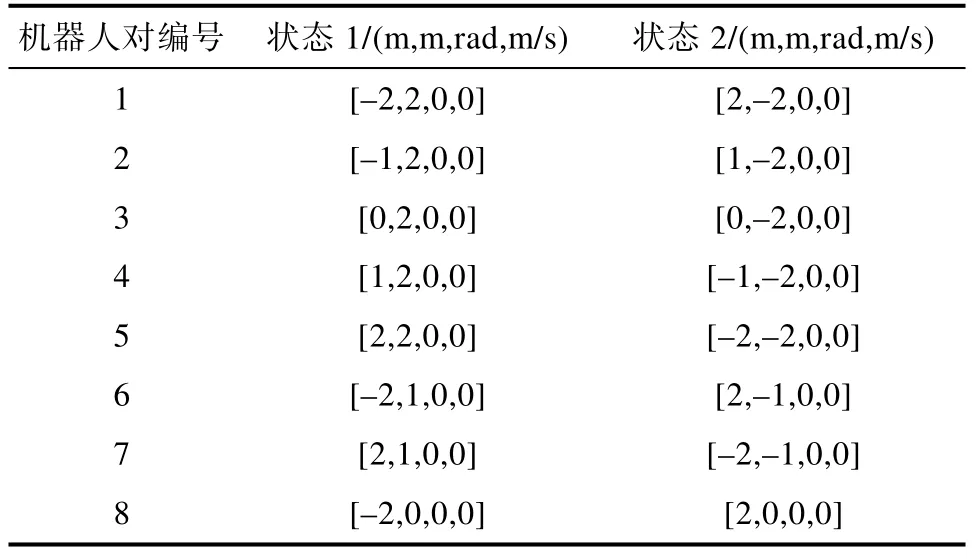
表1 轮式机器人始末状态Table 1 Starting and ending states of robot
三个圆形障碍物M=3 设置如表2 所示。

表2 圆形障碍物参数Table 2 Circular obstacle setting
序列凸优化算法参数设置如表3 所示。
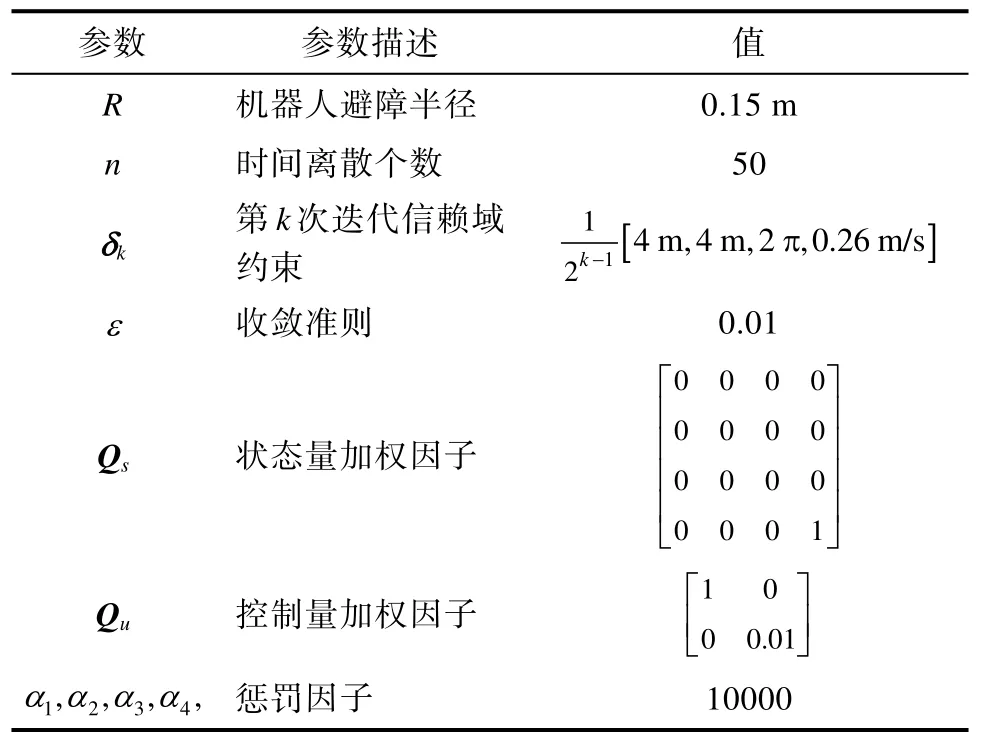
表3 序列凸优化算法参数Table 3 Algorithm parameters of SCP
由于状态量第四个分量为实际控制量中的v,因此状态量加权因子Qs的前三个对角元为零,仅用第四个对角元对实际控制量v进行二次加权。同理,控制量加权因子Qu第一个对角元表示了对实际控制量ϖ的二次加权,因此其与Qs第四个对角元量级相同。上述两参数取值物理意义为轮式机器人运动过程中能量最优。而控制量加权因子Qu第二个对角元减少了实际控制量v的变化,使得轨迹更加平滑,一般选取数值的数量级较小。
惩罚因子α1,α2,α3,α4, 对约束进行惩罚,一般取值较大以保证约束的满足。
仿真中,初始基准剖面选取为起始状态到目标状态的平均离散,该方法选取的初始基准剖面不一定满足初始问题P1 的动力学约束,随着迭代过程的增加,信赖域逐渐减小,最终收敛轨迹可在设定误差范围内满足P1 问题动力学约束。
针对上述设置的场景,求解机器人编队重构轨迹规划问题,轨迹规划结果如图5 所示,各个机器人均可抵达目标状态并且与圆形障碍保持安全距离,且在约束触发时各个机器人都从障碍边擦过,位于约束的临界状态。机器人相互避碰约束满足情况如图6 所示,机器人两两最小间距始终大于避碰安全距离,机器人在编队重构过程中满足相互避碰约束。物理性能约束满足情况如图7所示,物理性能指标(即式(3)左端)的最大值始终小于单轮速度上界,各个机器人在编队重构过程中满足个体物理性能约束。
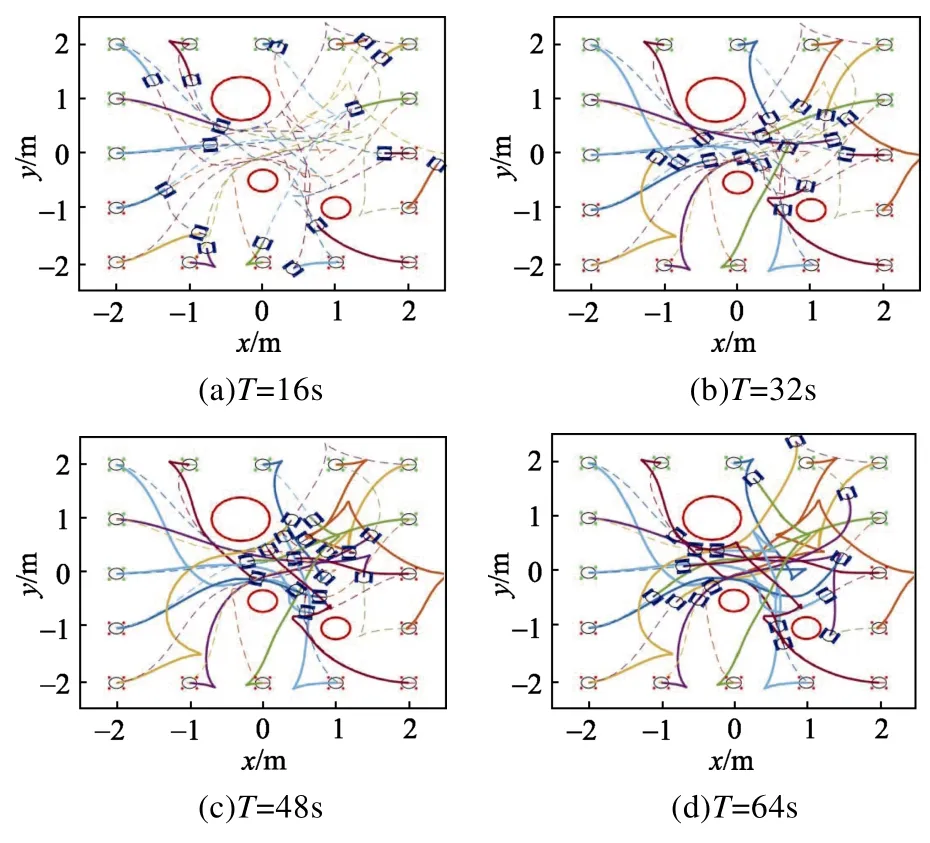
图5 规划轨迹结果图Fig.5 Planning trajectory result
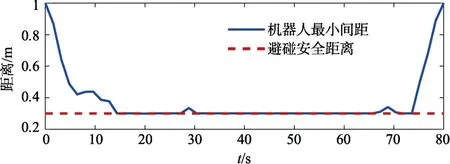
图6 避碰约束满足情况Fig.6 Obstacle avoidance constraint satisfaction result
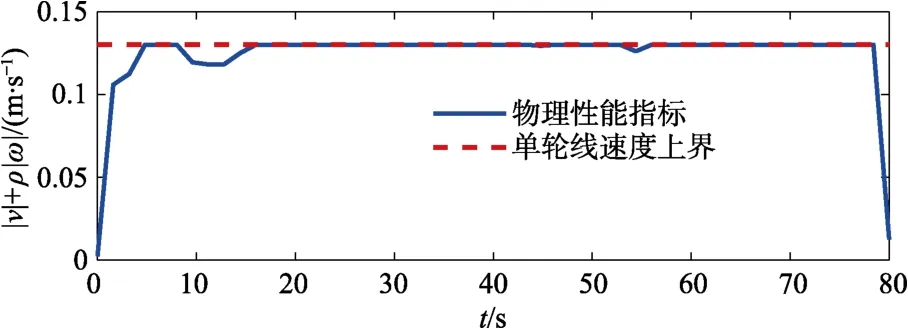
图7 个体物理性能约束满足情况Fig.7 Collision avoidance constraint satisfaction result
针对上述设置的场景,分别求解机器人对数为1 到8 的编队重构轨迹规划,对比SCP 方法与非线性优化工具包ICLOCS 在不同问题规模下的性能。当编队数量为8(N=8)时,编队由1~4对机器人组成。
使用SCP 方法和ICLOCS 分别求解不同编队数量的队形重构轨迹规划,多次统计求解时间与代价值进行对比。平均求解时间对比结果如图8所示,两种方法求解时间均随机器人个数增加而增加,SCP 求解时间远远小于ICLOCS 工具包求解时间。但从代价对比结果(图9)来看,SCP 在机器人数量较少时最优性更好,数量增加时ICLOCS代价值更小。其原因为ICLOCS 在优化过程中具有一定的随机性,每次优化的结果不同,这就使得其在面对多峰值高维问题时,较容易跳出局部 最优的状态,进而在时间足够的情况下得到较优的优化结果。实际应用中,需要考虑最优性与计算时间两方面的均衡,SCP 方法在尽可能保证最优性的同时大大缩短了计算时间,具有工程意义。
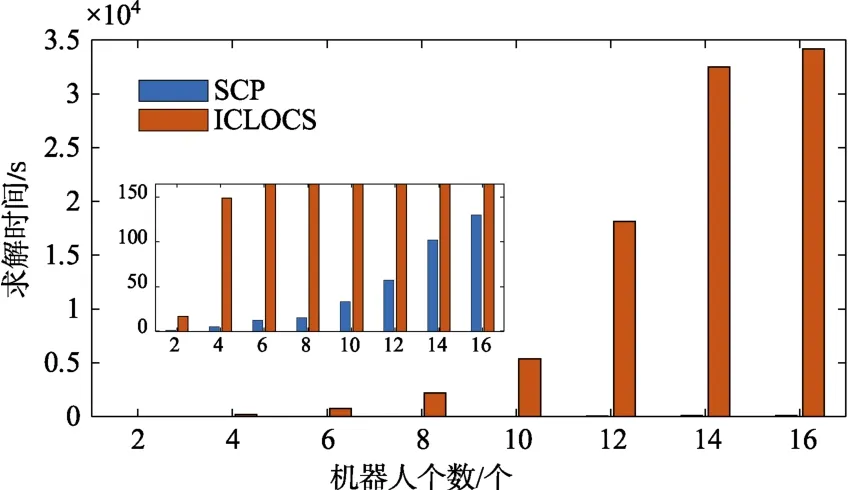
图8 平均求解时间对比Fig.8 Comparison of solution time

图9 平均求解代价对比Fig.9 Comparison of solution cost
6 结 论
本文针对多轮式机器人协同轨迹规划问题,根据现实物理约束,建立优化问题。将原始非线性优化问题转化为二阶锥优化问题,利用序列凸优化思想进行求解,进行仿真验证并得出了下面主要结论:
(1)建立了多轮式机器人协同轨迹规划的非线性优化问题,考虑了障碍规避、相互避碰以及机器人实际物理约束。
(2)对问题进行了凸化,包含运动学线性化、避障约束凸化、避碰约束凸化,并讨论了约束凸化的物理含义。使用梯形近似对问题进行离散化,并给出问题松弛处理方法。
(3)给出松弛SCP 方法求解协同轨迹规划问题的框架,并通过具体算例的数值仿真和对比验证了方法的有效性。
