可变电容式直线静电电机的驱动器设计

2021-04-17袁怡雯李华峰李锡龙

电子科技 2021年4期

袁怡雯，李华峰，李锡龙

(南京航空航天大学机械结构力学与控制国家重点实验室，江苏南京 210000)

静电电机已被广泛应用于微型电子机械系统领域[1]。与传统电磁式电机相比，毫米级静电电机能产生比相同尺寸的电磁电机更大的功率和力[2]。国内外对于正常尺寸的静电电机研究较少，目前还处于起步阶段[3-5]。本文所介绍的可变电容式直线静电电机为正常尺寸的设备。该电机由一对柔性薄膜组成，薄膜上分布着三相电极，三相电极整齐排列并且积累电荷。因为该类电机未使用铁磁材料，所以可在强磁场中完成一些特殊的任务。

静电电机投入到实际的使用中的困难之一是它的驱动电路。电机正常运转需要幅值为千伏级别的交流电压[6]。截至目前，日本东京大学设计了基于正弦波的驱动电路，根据驱动方法可将其分为3类：单频驱动法[7]、调制单频驱动法[8]、双频驱动法[9]。

上述3种方法中，单频驱动法存在电机低速运转时电机性能不稳定的问题[6]；调制单频驱动法产生的推力过小[10]；双频法需要两个三相高压信号，导致电源系统复杂，设计困难[11]。针对以上问题本文提出了使用方波信号驱动的方法，使静电电机按一定的步距前行，简化了驱动器的设计，使得静电电机在低速时具有不失步且推力稳定的优点。

1 静电电机的结构与驱动方法

本文从驱动电路的角度介绍了可变电容式直线静电电机的基本结构，并且详细介绍了静电电机的驱动方法。

1.1 可变电容式静电电机的基本结构

可变电容式直线静电电机包括动子和定子。电机外形如图1所示，定子固定在与其同宽的底板凹槽内，包含下板、粘贴在下板上的薄膜以及排列于薄膜表面的定子电极，且定子电极连接三相驱动电压。动子在下板上滑动，包含上板、粘贴在上板上的薄膜以及排列于薄膜表面的动子电极，且动子电极分别连接正极性驱动电压和负极性驱动电压。驱动电源与静电电机连接，用于输出三相驱动信号以驱动动子滑动。

图1 可变电容式直线型静电电机

1.2 静电电机的驱动方法

静电电机的运动的力来自于上下极板的电位差导致上下薄膜之间产生的静电斥力。静电斥力的法向分量起到减小定子和动子之间摩擦力的作用；静电斥力的切向分量沿定子表面推动滑块。定子和动子之间及电极之间都保留微米级别的间隙。为了减小定子和动子间的摩擦，在间隙中充入润滑油和微米珠。

定子上的6个铜电极和动子上4个铜电极为一组，电机上共m组定子电极和n组动子电极。每组电极中，定子电极依次由A相电压信号、B相电压信号、C相电压信号控制。动子电极依次与正极性驱动电压信号和负极性驱动电压信号相连接，连接图如图2所示。

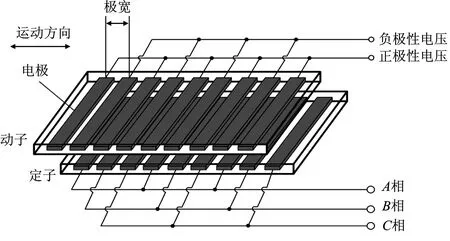
图2 动子电极和定子电极的驱动信号连接图

如图3(a)所示，A相和B相连接负极性驱动电压，C相连接正极性电压时，动子有向左和向右振荡的趋势，但最后都被静电力牵制而保持静止，此状态称为平衡态。若改变A相极性，上下极板间的静电力使动子获得一个稳定的向右的力，直至运动到图3(b)的平衡位置。到达图3(b)的平衡位置后，改变C相的极性，静电力使动子继续获得一个向右的力来运动到达图3(c)的平衡位置。到达图3(c)的平衡位置后，改变B相的极性，动子在静电力的推动下继续向右运动到下一个平衡位置。所以按照A-C-B相的顺序改变极性电机将获得稳定的前进的动力。通过分时供电和多相时序控制电压，即可使静电电机正常工作。

图3 静电电机运动示意图

静电电机的转速和停止位置取决于驱动器提供的电压脉冲的频率和脉冲数。当静电电机接收到一个脉冲信号，动子就会按照设定的方向滑动固定的距离，这个距离称作“步距”。静电电机的运动可以看作是一步一步在进行。控制脉冲的个数就可以控制静电电机前进的步数，从而实现电机的精准停止。同时，控制脉冲的频率可以控制电机的运动速率，达到调速的目的。

1.3 驱动方案的仿真验证

现有的静电电机的驱动方案均基于正弦波。虽然正弦波的驱动信号下的静电电机的性能已经被各国研究人员经软件仿真计算和实验实际测量得出了确切的结论，但是使用方波驱动是否可行尚没有一个确定的答案，故软件仿真验证必不可少。

考虑到仿真操作的方便性和准确性，本文仿真实验使用Maxwell软件[12]，求证静电电机的动子到达平衡位置后，定子进行换相动作，动子在换相瞬间受的力是否为最大。在Maxwell的静电场求解器中有5个边界条件，即默认边界条件、狄里克边界条件、气球边界条件、对称边界条件和匹配边界条件[13]。静电电机的有限元模型建立后，定义自然边界条件和诺依曼边界条件为

E1t=E2t

(1)

φ1=φ2

(2)

D1n-D2n=σ

(3)

(4)

其中，E表示场强；ψ表示电势；Dxn表示电位移矢量Dx在曲面某点处法线上的分量。动子电极和定子电极为等电位体，表面为等电位面，符合狄里克边界条件。

E=-∇φ

(5)

电机外层的空气介质符合气球边界条件，故用来模拟无限远处点位为零的情况。有限元模型如图4所示，矩形1和矩形3分别为动子材料和定子材料polyimideQuartz，矩形4～17为铜电极材料copper，矩形2为绝缘性物质。电机的尺寸参数与样机相同，定子电极4、7、10、13接入A相电压UA；定子电极5、8、11接入B相电压UB；定子电极6、9、12接入C相电压UC；动子电极14、16接入1 000 V电压、动子电极15、17接入0 V。

图4 静电电机有限元模型

模拟电机的6个状态，得到了如图5～图10的6个受力图。由图中可以看出，动子的受力呈近似正弦的变化趋势且呈周期性变化。动子受力最大为0.45 N，最小为-0.45 N，受力最大处每次滞后半个定子间距的长度，符合上文中对电机运动时的分析。

图5 状态1

图6 状态2

图7 状态3

图8 状态4

图9 状态5

图10 状态6

用同样的方法进行MATLAB仿真，得到图11的结果。该结论与Maxwell一致，证实了方案的可行性。

图11 动子力MATLAB仿真图(6种模态)

2 1 000 V可调直流电源设计

高压直流可调电源是驱动器能量的来源，电源的质量直接决定驱动器性能的好坏[14-15]。

驱动器要求电源1 000 V可调输出，纹波小，输入电压为15 V，故基于推挽拓扑的升压结构比较合适。电源结构框图如图12所示。

图12 电源结构框图

如图13所示，推挽升压拓扑结构可看成两个单端正激变换器。电路主要由驱动芯片、MOSFET、变压器组成。驱动信号为相位差180°的脉宽调制波，其中MOSFET交替打开，并存在死区。

图13 推挽升压拓扑

推挽拓扑的输入输出电压满足以下计算式

Vout=2VinnD

(6)

其中，Vout为输出电压，Vin为输入电压；n为匝数比；D为占空比。在占空比D为0.45时计算出n为74.074。考虑到电路中的损耗，此处选择匝数比n为75。

此外，为了减小电源的体积，驱动信号频率设为25 kHz。又由于电源在高频的情况下工作，故选择使用铁氧体作为变压器的磁芯材料。

根据AP法计算磁芯型号。AP即磁芯窗口面积与磁芯有效截面积的乘积，其计算式为

(7)

其中，AP为磁芯截面积窗口面积乘积；Ac为磁芯有效截面积；Am为磁芯窗口面积；PT为变压器功率；Bm为磁芯最大工作磁感应强度；f为变压器工作频率；KW为变压器的窗口占空比系数；Kj为电流密度系数。通过查询相关手册，在25 kHz时，Bm为0.2 T，KW取0.3，Kj取366(EI型磁芯为25 ℃时)。结合式(8)进行计算。

(8)

在输出功率Pout为10 W，效率η为90%时，计算得到变压器功率PT为25.7 W，AP为0.08 cm4。查询磁芯手册，找到合适的磁芯型号E33。

为了减小输出信号的波纹并保证电源输出性能的稳定性，电源加入了整流滤波电路，并使用整流桥代替整流二极管来减小电源体积。滤波电路采用电容和电感串联的方式。在单片机STM32上接入电位器使电源输出电压可调。最终完成的1 000 V可调直流电源如下图所示。

图14 1 000 V可调直流电源

3 驱动电路的设计

驱动电路需实现以下功能：(1)单片机的6个定时器通道按照一定的时序输出6路PWM(Pulse Width Modulation)波，用以控制半桥驱动电路中的6个MOSFET的开通和关断；(2)驱动芯片将单片机输出的3.3 V的PWM信号放大成为12 V的电信号；(3)半桥驱动电路在PWM波的控制下可以输出三相方波电信号分别给静电电机的A相电极、B相电极和C相电极。

驱动拓扑如图15所示，由3个驱动芯片和6个MOS场效应晶体管组成。该电路可以看作是由3个半桥电路并联而成。每个半桥电路中，仅有一个MOSFET输出正极性电压，另一个输出负极性电压，上下开关管间有一定的死区来避免同时导通发生错误。通过控制6个MOS场效应晶体管按时序导通和闭合可以获得正确的电压方波信号。