直线超声电机定/动子接触的微观力学模型

周胜利，姚志远

(南京航空航天大学 机械结构力学与控制国家重点实验室，南京 210016)

直线超声电机具有结构简单、直接驱动、推力比大、响应快、断电自锁、定位精度高等优点，在航空航天，武器装备和精密驱动等领域具有重要的应用前景，其研究也受到越来越多的关注[1－4]。

直线超声电机的动力学建模是超声电机研究的重要内容。不仅有助于理解超声电机的运行机理，实现电机结构的优化设计、运行控制和寿命估计，且有利于提高电机运行的稳定性。

动力学建模主要包括建立自由定子的振动模型，定/动子的接触模型和机电耦合模型。由于直线超声电机通过定/动子的摩擦作用驱动动子运动，因此分析定/动子的摩擦机制，建立正确的定/动子接触模型是建立超声电机动力学模型的前提。

在国内直线超声电机的研究落后于行波超声电机[5－6]，当前的研究热点是其结构设计，尚缺乏动力学建模的研究。许海等[7－8]在对直线超声电机进行动力学建模时，对摩擦界面采取了与传统行波超声电机类似的办法，即假设定/动子有光滑的接触表面，定/动子间有一可等效为线性弹簧的摩擦层。而实际的定/动子接触表面是粗糙的，且定/动子间并无摩擦层的存在。目前尚未见到有关直线超声电机定/动子接触表面摩擦学调查研究，以及粗糙表面对定/动子运行特性影响研究的报道。

本文以南京航空航天大学精密驱动所研制的V型直线超声电机的表面微观力学特性为研究对象，首先通过实验测试了定/动子接触表面的粗糙度和统计参数，并基于概率统计方法得到了定子接触表面各点高度的概率分布函数，通过伪随机数模拟的方法给出接触表面的模拟模型;再通过赫兹微观接触模型建立定/动子接触的微观力学模型。在此模型基础上得到了定/动子的预压力和接触变形量和真实接触面积之间的关系。

1 定、动子接触界面的微观表面特性

V型直线超声电机的定子由两变幅杆组成，端部有一驱动足，材质是45钢，动子接触表面为Al2O3陶瓷，电机实际工作时，预压力一般在30～80 N之间。利用4 000倍光学显微镜拍得摩擦后定/动子接触表面形貌如下:

图1 定子接触表面形貌Fig.1 The morphology of stator’s contact surface

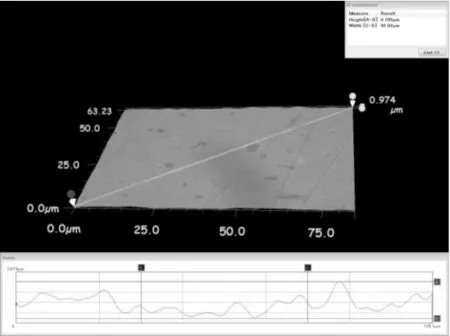
图2 动子接触表面形貌Fig.2 The morphology of mover’s contact surface

其中，AB为采样线段。对其上各点高度进行均值化处理(各点高度减去所有点高度的平均值)后，其形貌曲线见图5虚线部分。

经调查计算，摩擦后定/动子接触表面特性如表1所示:

由表1可知，动子接触表面比定子接触表面光滑的多，且弹性模量和硬度要大得多。利用SPSS软件对定子接触表面在采样线段AB上各点高度进行统计分析，得其关于正态分布的P－P图如图4。

图3 动子接触表面轮廓曲线Fig.3 The contour curve of mover’s contact surface

图4 P－P图Fig.4 The P － P figure

图5 伪随机数表面模拟1Fig.5 Surface simulation by pseudo-random number 1

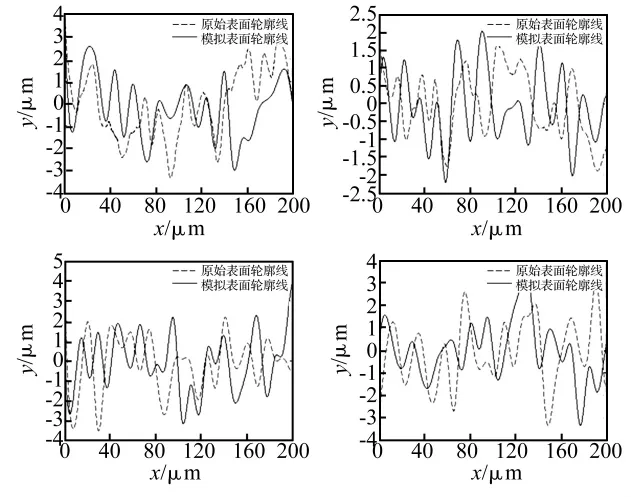
图6 伪随机数表面模拟2Fig.6 Surface simulation by pseudo-random number 2

表1 定/动子接触表面统计参数Tab.1 Statistical parameters of stator’s and mover’s contact surface

由图可见，图中各点近似呈一条直线，说明定子接触表面上各点高度服从正态分布[11]。定子接触表面上各点高度的概率分布函数为:

其中方差 σ2=1.12。

利用matlab生成服从上述概率分布的伪随机数的方法来模拟定子接触表面的表面轮廓线如下:

图5表明，伪随机数模拟的方法可模拟摩擦后定子接触表面形貌。用该方法模拟另外四条表面轮廓线如下，由此可证明该方法是有效的。

2 定/动子接触表面的微观力学分析

2.1 物理模型

实际上定/动子接触表面是粗糙的，由许多高度不一的微凸体和凹谷组成。为简化计算，假设:

(1)动子表面刚性光滑平面，定子表面粗糙;

(2)定/动子接触时只定子发生变形，且变形完全弹性变形，变形时各微凸体之间无相互作用。

(3)每个微凸体都是半径不等的球体组成，球体在动子刚性光滑平面的作用下发生变形，其变形量和受力大小的相互关系满足Hertz接触理论。

(4)直线超声电机的定、动子接触在Oxy平面。考虑Oxy平面的正方形区域，认为在该区域内定子表面微凸体排列成n×n的方阵，一行或一列上的接触压力为，整个正方形区域上的接触压力为

(5)取一行微凸体，沿行方向作剖切面的轮廓线由随机数模拟的方法给出，如图6所示。

实际上，若已知单个微凸体上所承受压力与变形量、实际接触面积之关系，可由Hertz描述。由于表面轮廓线已知，即可求出在这一区域内的总压力与总变形量、总实际接触面积之关系。

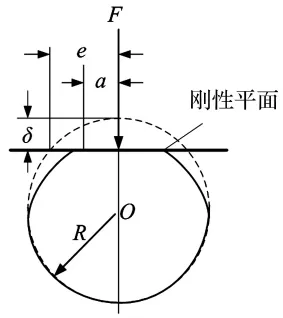
图7 单粗糙峰弹性接触Fig.7 Single asperity elastic contact

2.2 Hertz接触模型

依据以上假设，动子是由刚性、平整的陶瓷材料组成，它构成了一个刚性平面;而定子是由弹性、粗糙的45钢材料构成，构成了一个由若干个半径不等的半球体组成的弹性曲面。首先研究单个球体与刚性平面接触的问题，根据Hertz接触理论[10]，图7展示单个球体在压力F下变形状态。

图中，F为载荷;δ为变形量;实际接触区域是以a为半径的圆，而不是以e为半径的圆。

在弹性范围内有:

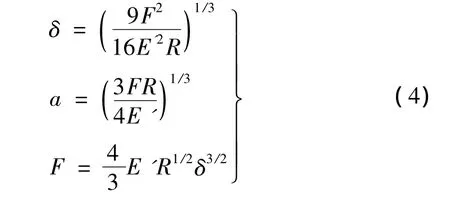
实际接触面积:

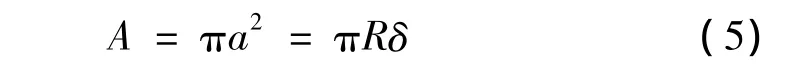
2.3 数值仿真计算

以图7所示轮廓曲线为研究对象，仿真计算的正方形区域面积为0.2×0.2 mm2。定子驱动足表面积为16 mm2，实际表面的压力、接触点数和接触面积是前者相应量的400倍。数值计算该区域内的总压力F与实际接触面积SF之间关系的算法如下:

(1)给定动子刚性平面在预压力作用下的位置高度z;

(2)通过表面轮廓线找到轮廓线与动子刚性平面等高的点{xk}，并从中确定其微凸体所在的区域{x1k，为微凸体的个数。

(3)由区间[x1k，x2k]中波峰坐标[x'k，y'k]和区间端点坐标[x1k，0]、[x2k，0]插值出与微凸体等效的半球体，并得到半球体的半径rk和变形量 δk。

(4)由式(4)计算出每个半球体上的载荷Fk，进而得到该正方形区域上的总载荷F。

(5)由式(5)计算出每个半球体上的实际接触面积Ak，进而得到总的实际接触面积SF。

由上述算法可得定子驱动足变形量与预压力之间的关系如图8所示。

用二次函数拟合，有:

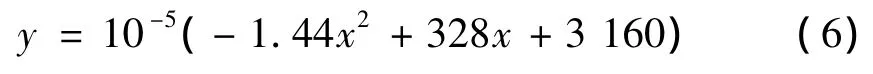
实际接触面积与变形量的关系如下:

用线性函数拟合，有:

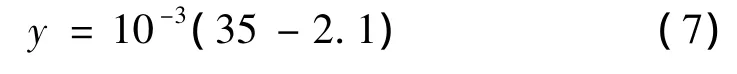
实际接触面积与预压力之间的关系如图10所示。

用线性函数拟合，有:

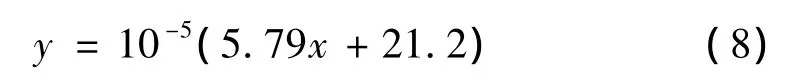
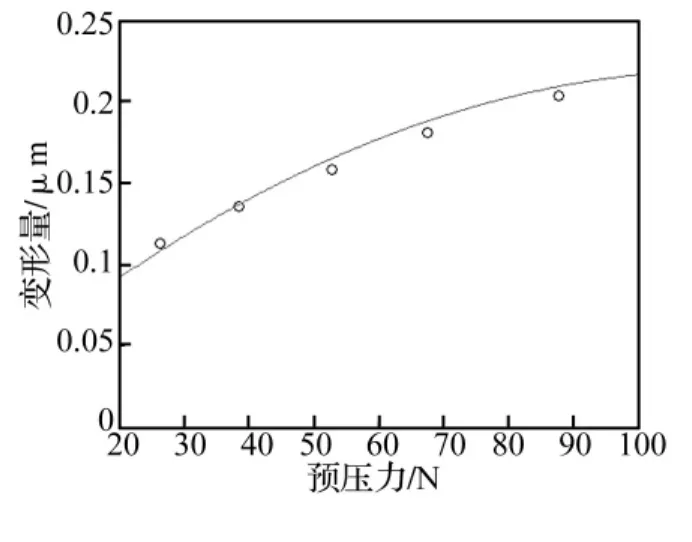
图8 变形量与预压力的关系Fig.8 The relationship between deformation and pre-stress

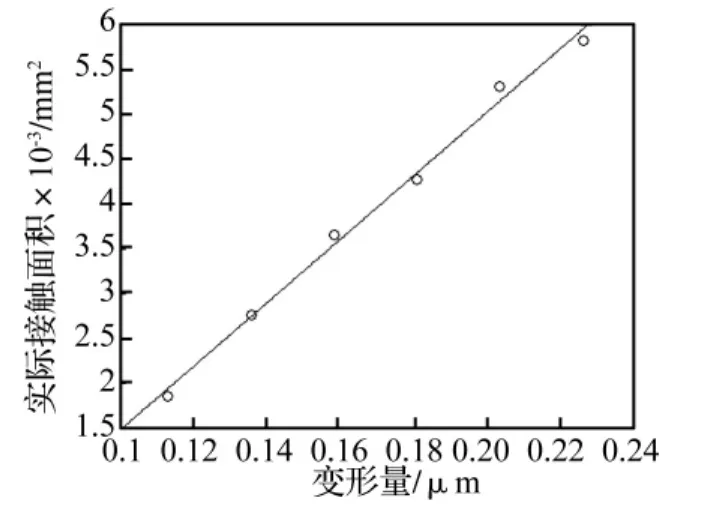
图9 实际接触面积与变形量的关系Fig.9 The relationship between real contact area and deformation

图10 实际接触面积与预压力之间的关系Fig.10 The relationship between real contact area and pre-stress

3 结论

本文利用伪随机数的表面模拟方法模拟摩擦后定子的接触表面形貌，并建立了相应的微观接触力学模型，计算结果表明:

(1)陶瓷的硬度和弹性模量都比45钢大得多，且摩擦后的动子接触表面粗糙度比定子接触表面粗糙度低得多，故在建模时，可认为动子接触表面是光滑刚性的。

(2)接触变形量随预压力的变化呈2次多项式的变化规律，在电机正常工作时，变形量一般在0.1－0.2 μm之间。

(3)定/动子实际接触面积随预压力的变化近似为线性变化规律，在电机正常工作时，实际接触面积在0.002－0.005 mm2之间，只占名义接触面积中极小的一部分。

(4)通常驱动足振幅在0.3－0.4 μm 之间，而接触变形量在0.1－0.2 μm 之间，表明定、动子的接触层起非线性的弹簧作用，对电机的振动产生影响。

分析反映了实际直线超声电机定/动子接触的状况，研究有助于建立直线超声电机的整体动力学模型和分析摩擦摩损特性。

[1]赵淳生.超声电机技术与应用[M].北京:科学出版社，2007.

[2]Yao Z Y，Zhao C S，Zeng J S，el al.Analytical solution on the nonlinear vibration of a traveling wave ultrasonic motor[J].Electroceram，2008，20:251 －258.

[3]Hemsel T，Wallaschek J.Survey of the present state of the art of piezoelectric linear motors [J].Ultrasonics.2000，38:37－40.

[4]姚志远，吴 辛，尹育聪，等.超声电机定子和转子接触微观表面分析和形貌模拟[J].润滑与密封，2009，34(6):5 －7.

[5]朱 华，陈 超，赵淳生.行波型杆式超声电机的动力学分析与性能仿真[J].振动与冲击，2008，27(6):103－107.

[6]陈 超，曾劲松，赵淳生.旋转型行波超声电机理论模型的仿真研究[J].振动与冲击，2006，25(2):129－133.

[7]许 海，赵淳生.直线型驻波超声电机的定、动子间接触及摩擦分析[J].南京航空航天大学学报，2005，37(2):144－149.

[8]许 海，李志荣.直线驻波型超声电机的接触分析和堵转推力模型[J].微电机，2010，43(5):19 －21.

[9]许 海，赵淳生.双足型直线超声电机的结构及实验[J].振动与冲击，2007，26(6):100 －102.

[10]Hertz H.Uber die beruhrung fester elastische korper and uber die harte(on the contact of rigrid elastic solids and on hardness)[M].jLeipzig，Verhandlungen des Vereins zur Beforderung des Gewerbefleisses，1882.

[11]魏宗舒.概率论与数理统计[M].北京，高等教育出版社，1996.