间断Galerkin方法中的加权本质无振荡限制器述评

邱建贤,朱 君

(1.厦门大学数学科学学院，福建 厦门 361005;2.南京航空航天大学理学院，江苏 南京 211106)

间断Galerkin(DG)方法具有坚实的数学理论和实现方法，易于处理各类复杂区域和边界问题，可实现高效并行和各类网格，非常适合于计算流体力学(CFD)、计算气动声学、计算电磁学等相关工程问题的计算，DG方法已成为目前CFD高精度数值方法的研究热点之一，也是下一代CFD解算器高精度仿真的首要选择.非线性双曲守恒律方程作为流体力学中的重要方程，即使初始值光滑，其解也可能产生间断，如激波等.而对于存在强间断解的数值模拟中，DG方法容易产生较为明显的非物理振荡，进而产生非线性不稳定，导致数值解爆炸.所以对于此类问题往往需要使用非线性限制器来抑制非物理振荡，从而实现相关物理过程的准确、稳健的数值模拟.而常用的限制器(如：总变差减小(TVD)限制器、总变差有界(TVB)限制器等)虽然可以控制间断附近的伪振荡，但是它们不仅会过渡抹平激波(包含需要人为调整的参数)，而且会降低DG方法的预期设计精度.另一方面，由于限制器的引入，修改了原DG的解，会造成解在局部不匹配，从而影响定常问题的收敛性.因此，近十年来，本课题组一直致力于DG紧致格式的高精度非线性限制器的研究，提出并发展了一系列兼具高精度、强稳健及紧致特性的限制器，在促进基础算法发展的同时已广泛应用于相应工程领域.

间断有限元方法最早由Reed等[1]为解决中子输运方程(线性双曲方程)而提出的，它的一个很重要的发展是Cockburn等[2-6]构建了发展型的非线性双曲守恒律的Runge-Kutta DG(RKDG)方法.这种DG方法[7-13]属于线方法范畴，在时间离散系统中采用非线性稳定的高精度Runge-Kutta方法，在空间的离散系统中，DG有限元方法，界面间的数值通量采用真正的或逼近的Riemann解，并且使用TVB的限制器，得到了即使在强激波情况下也无伪振荡的性质.此外，Dumbser等[14-15]在每个时间步使用重构算子来增加高阶DG方法的数值精度和稳定性.文献[16-20]提出了拉格朗日DG方法.Tia等[21]应用泰勒基构造了DG谱有限元方法.Hex等[22]设计了 一种新的加权RKDG方法用于求解三维声波和弹性波，并为解扩散方程提出了rDG方法[23-24].由于DG方法优越的计算性能，该方法也被广泛用于流体力学等科学计算领域[25-31]，其他的高阶经典DG方法参见文献[32-34].由于有限元的特性，DG方法和古典的有限差分和有限体积法相比有以下的优点：1)DG精度的阶仅依赖于精确解.DG的阶可通过适当选取逼近解的多项式的次数得到.2)DG方法具有高度的可并行性.3)单元划分及对边界处理的灵活性高，适合于处理复杂的区域的问题.4)DG方法易于进行自适应处理，自适应算法在具有间断的双曲问题的求解中非常重要.目前，DG方法已广泛应用流体动力学、湍流、天气预报、粒子流、海洋学、油气储藏模拟、浅水模型、多孔介质中流体输运、半导体的模拟、电磁场、图象处理等问题中，是目前CFD高精度数值方法的主流算法之一.

在DG方法的构造中，限制器是一个很重要的组成部分，它可以控制格式在间断问题(如激波)计算中产生伪振荡，且必须采用限制器，保证格式的稳定性.通常限制器的过程可以分为两个部分：首先确定“坏单元”(“Troubled-cell”)，即解含有间断的单元，在该单元需要做限制过程；然后在“坏单元”中修正DG的多项式解，由于守恒的要求，需要保证单元平均值不变，同时保证与原DG的解具有相同的精度，且振荡减小.

在第一部分中，使用“坏单元”或称间断指示器，如基于最小模型指示器[4]，基于力矩的指示器[35]，以及改进的力矩指示器[36]，基于DG超收敛性质的KXRCF指示器[37]，基于Harten子单元分辨方法的指示器[38]等.

在第二部分中，包括经典的最小模型限制器[2-4,6]，基于力矩的限制器[37]，以及改进的力矩限制器[36]等.这些限制器属于斜率型限制器的范畴，它们的优点是可以在强间断附近有效抑制伪振荡的出现，但付出的代价是在解的光滑极值点处有可能降低格式的数值精度.另一种类型的限制器是基于本质无振荡(ENO)和加权ENO(WENO)方法[39-46]的思想构造的，具有很强的激波穿透能力和保持格式的高精度.这种类型的限制器通过将问题单元上的DG方法数值解的自由度进行重构，可以在解的光滑区域实现高精度并在强间断附近保持本质无振荡的性质.这些高精度WENO限制器基本上均为根据有限体积WENO格式的构造方法设计的，随着DG方法格式精度的提高该限制器需要更宽的空间模板，有时会破坏原始DG方法本身具有的空间模板紧凑的性质.此外，众多的WENO限制器[47-54]，包括新型WENO限制器[51,55-57]，自适应阶WENO限制器[58]，中心型WENO(CWENO)限制器[59]，和HermiteWENO(HWENO)限制器[48,50,60]等都是第二类型的限制器.此外，由于CWENO格式[61-64]比经典的WENO格式[65-67]在数值计算上的代价更低，它们可以作为DG格式的后验子单元限制器[30].

基于上述研究，本课题组近十年来一直致力于DG方法的高精度WENO限制器的研究工作，提出并发展了一系列兼具高精度、强稳健及紧致特性的限制器，在促进基础算法发展的同时已广泛应用于相应工程领域.主要包含如下工作：针对已有限制器不能保持DG方法高精度或需要选取参数的问题，结合DG方法和有限体积WENO格式的优良特性设计了WENO限制器，有效地解决了限制器中含有参数和在部分光滑区域中降低DG方法数值精度的问题，实现了对非线性双曲守恒律的数值模拟，并通过数值结果验证了该类WENO限制器的一致高精度、无振荡和高分辨率等特性，解决了经典WENO限制器的模板比DG方法模板更宽的问题；将Hermite插值理论用于限制器构造过程设计了HWENO限制器，有效地缓解了WENO限制器宽模板问题，进而更好地发挥DG方法的作用，实现了对结构网格和非结构网格上非线性双曲守恒律的数值模拟；为了更好地模拟具有高频振荡的物理问题，设计了一类基于三角基函数空间的TWENO格式，并将其发展为DG方法的限制器.该限制器在相同条件下，能够更好地数值求解复杂波形或高频振荡问题；为了减少传统WENO限制器构造过程过于复杂繁琐以及解决宽模板问题，设计了一类紧凑简单的新型HWENO限制器，该限制器解决了经典WENO限制器的构造破坏了DG方法紧致性的弊端，且避免了线性权在复杂网格体系下的计算，从而大大提高了计算效率.

1 DG方法简述

首先考虑一维标量守恒律方程

(1)

(2)

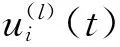
(3)

(4)

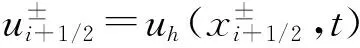
(5)

(6)

2 高精度限制器

2.1 TVB问题单元间断指示器[4]

定义

从式(2)可以看出

这是修改的标准minmod限制器[70]

其中m定义为

(7)

或者定义为TVB修正的minmod函数[71]

(8)

使用上述TVB问题单元指示器识别问题单元.其中M>0是常数且M的选择取决于问题的解.对于标量情形，可以通过文献[4]中的初始条件估计M(M与初始条件在光滑极值处的二阶导数的绝对值成正比)；然而，在方程组情形下较难估计M.如果M选择得太小，DG方法的数值精度可能在解的光滑极值点处降低；如果M选择得太大，DG方法会在解的非光滑区域产生伪振荡.由于下面介绍的高精度WENO限制器可以在问题单元上对DG方法数值解中的自由度进行重构时保证格式的高阶精度不被破坏，所以是否选择一个精确的M就显得不太重要.

2.2 KXRCF间断指示器[39]

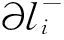
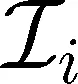
(9)

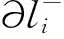
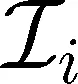
2.3 WENO限制器

2.3.1 重构步骤1

在高斯或高斯-洛巴托积分点上重构u的点值.对于Pk的DG方法(k+1阶精度)，需要使用至少达到2k+2阶精度的高斯或高斯-洛巴托求积公式，WENO重构的数值精度至少必须达到2k+1阶.为此，本课题组需要用2k+1个相邻单元Ii-k，…，Ii+k的单元平均值构造多项式并在高斯或高斯-洛巴托求积节点上得到u的高阶逼近值.然后执行如下重构步骤[41-42,72]:

2)计算线性权γ0,…，γk.在不同的高斯或高斯-洛巴托求积节点xG上满足

对应的一组线性权为

对应的一组线性权为:

3)计算光滑指示器βj，用于衡量问题单元Ii中代数多项式pj(x)的光滑程度.光滑指示器βj越小，问题单元中的代数多项式pj(x)越光滑[41,72]:

(10)

光滑指示器βj常被写成u的单元平均值的二次方形式，详情参见[41,43,72].

4)根据光滑指示器计算非线性权

(11)

其中γj是上述步骤2)中确定的线性权，ε取一个避免分母为零的小正数.最终的近似值为

(12)

2.3.2 重构步骤2

基于2.3.1重构的点值u(xG)和数值积分获得自由度的重构值.

对于方程组情形，WENO限制器总是与局部特征分解一起使用，详情参见文献[43].三角形和四面体网格上使用DG方法结合WENO限制器求解双曲守恒律方程组的详细过程如下[57,73]：首先在非结构网格上使用TVB问题单元指示器识别出问题单元，通过使用相邻三角形(四面体)的单元平均值进行WENO重构，在保持问题单元上物理量的单元平均值不变的情况下得到重构多项式并对其上DG方法数值解的自由度进行修正.

2.4 HWENO限制器

在本小节中，本课题组将HWENO重构过程应用于2.3.2节.该重构过程的优点是可在保持DG方法相同数值精度的同时有效减少所用空间模板的个数和降低模板的空间尺度，使之具有更好的空间紧凑性.在此，基于一维标量守恒律方程(1)来介绍三阶精度(k=2)HWENO限制器的构造情况[73].

1)给定小模版S0={Ii-1,Ii}，S1={Ii，Ii+1}，S2={Ii-1,Ii,Ii+1}和大模板T={S0,S1}，构造Hermite二次重构多项式p0(x),p1(x),p2(x)和四次重构多项式q(x):

得到：

2)计算线性权γ0,γ1和γ2.由

得到

3)根据式(10)计算光滑指示器βj，然后根据式(11)计算非线性权.重构多项式的第一个自由度为

(13)

1)给定小模版S0={Ii-1,Ii}，S1={Ii,Ii+1}，S2={Ii-1,Ii,Ii+1}和大模板T={S0，S1}，构造Hermite三次重构多项式p0(x)，p1(x)，p2(x)和五次重构多项式q(x):

得到：

2)计算线性权γ0,γ1和γ2:

得到

3)根据式(10)计算光滑指示器βj，然后根据式(11)计算非线性权.重构多项式的第二个自由度为

(14)

本小节只考虑了一维HWENO限制器的构造流程，该限制器可以推广到多维情形.文献[74]详细地介绍了使用DG方法结合HWENO限制器在非结构网格上求解三维非线性双曲守恒律方程组.同样该文首先在三维四面体网格上使用TVB问题单元指示器找出问题单元，然后通过使用相邻四面体的单元平均值或导数平均值，在保持问题单元上物理量的单元平均值不变的情况下进行HWENO重构，得到问题单元内的多项式并对其上DG方法数值解的自由度进行修正.

2.5 TWENO限制器

……

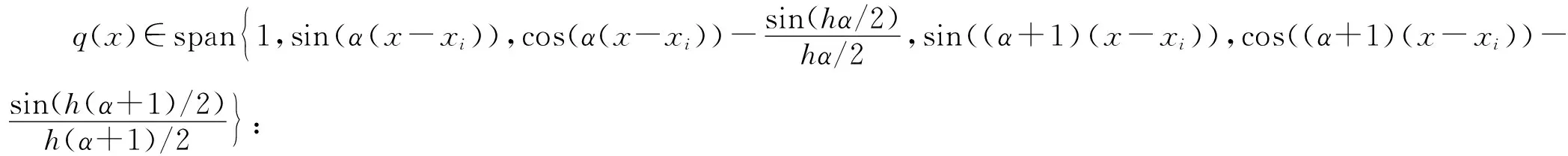
(15)

(16)

和

(17)

γ1=(cos(h(-1+α))-cos(h(2+α))+

cos(h(2+3α))-cos(h+3haα)+4hsin(hα)+

4hαsin(hα)-2hsin(2hα)-2hαsin(2hα)-

4hαsin(h(1+α))+2hαsin(2h(1+α)))/

γ2=1-γ1-γ3,

γ3=((-cos(h(-1+α))+cos(h(2+α))-

cos(h(2+3α))+cos(h+3hα)+2hsin(h)+

4hαsin(h)+hsin(h(-1+α))+hαsin(h(-1+

α))-hαsin(h(2+α))-hαsin(h(2+3α))-

2hsin(h+2hα)+hsin(h+3hα)+hαsin(h+

γ1=(-cos(h(-1+α))+cos(h(2+α))-

cos(h(2+3α))+cos(h+3hα)+2hsin(h)+

4hαsin(h)+hsin(h(-1+α))+hαsin(h(-1+

α))-hαsin(h(2+α))-hαsin(h(2+3α))-

2hsin(h+2hα)+hsin(h+3hα)+hαsin(h+

γ2=1-γ1-γ3,

γ3=(cos(h(-1+α))-cos(h(2+α))+

cos(h(2+3α))-cos(h+3hα)+4hsin(hα)+

4hαsin(hα)-2hsin(2hα)-2hαsin(2hα)-

4hαsin(h(1+α))+2hαsin(2h(1+α)))/

3)根据式(10)计算光滑指示器：

4hα(ui-1-ui-2)(ui-1-ui)cos(hα)+2(ui-1-

ui-2)(ui-1-ui)sin(hα)-(ui-2-ui)(-2ui-1+

ui-2+ui)sin(2hα)-2(ui-1-ui-2)(ui-1-

ui)sin(3hα)-(ui-1-ui)2sin(4hα)+

4hα(ui-1-ui-2)(ui-1-ui)cos(hα)-2(ui-1-

ui-2)(ui-1-ui)sin(hα)+(ui-2-ui)(-2ui-1+

ui-2+ui)sin(2hα)+2(ui-1-ui-2)(ui-1-

ui)sin(3hα)+(ui-1-ui)2sin(4hα)))/256,

cos(hα)-4(-1+h2α2)(ui-1-ui)(ui-ui+1)

sin(2hα)))/256,

(ui+1-ui+2)cos(hα)+2(-1+h2α2)(ui-ui+1)

2h2α2uiui+1sin(2hα)+2ui+1ui+2sin(2hα)-

2h2α2uiui+2sin(3hα)+2ui+1ui+2sin(3hα)-

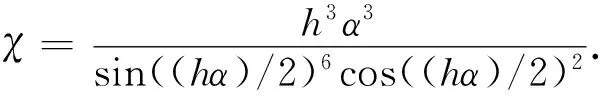
4)根据式(11)计算非线性权叫ωn,n=1,2,3.并通过高斯-洛巴托求积点xG处的重构点值u(xG)和数值积分得到

(18)

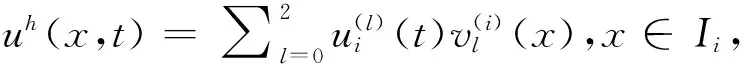
本小节介绍了三角函数多项式空间中TWENO限制器的构造过程.其构造思想与前面类似，首先使用TVB问题单元指示器找到问题单元，然后使用相邻单元的单元平均值通过TWENO限制器在问题单元内重构三角函数多项式.文献[74]中的数值结果表明，当基于三角函数多项式空间的格式用于模拟波类和高频振荡问题时能得到更好的数值结果.

2.6 简单紧凑型HWENO限制器

首先使用KXRCF问题单元指示器[37]来检测问题单元，接着在一维标量情况下阐述简单紧凑型HWENO限制器的构造过程.具体过程如下所示：

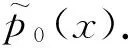
(19)

(20)

(21)

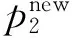
2)选择线性权γ0,γ1，γ2.如文献[51]所述，本课题组在3个单元Ii-1，Ii+1，Ii中使用了3个多项式p0(x)，p1(x)，p2(x)的完整信息，因此线性权只需任意选择和为1的正数即可保持高阶数值逼近.

3)参照式(10)计算光滑指示器，参照式(11)计算非线性权.

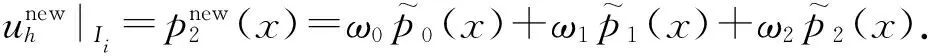
二维结构网格和三角形网格上简单紧凑型HWENO限制器的构造过程参见文献[54，75].该简单紧凑型HWENO限制器的主要创新点是重构过程仅使用来自问题单元及其近邻单元的DG方法数值解的信息，空间模板非常紧凑.在重构过程中使用的线性权不再需要根据计算网格的空间拓扑结构通过繁冗的数值计算获得，可以是任意和为1的正数.因此，该限制器能在结构网格、非结构网格、杂交网格、运动网格、自适应网格等情况下灵活使用且对网格质量要求较低.

2.7 Multi-resolution WENO限制器

本小节借鉴multi-resolution方法[76-86]构造了一种新型multi-resolution WENO限制器[87-88].本课题组仍在结构网格上针对一维标量双曲守恒律方程(1)构造multi-resolution WENO限制器[89].具体过程如下所示：

(22)

(23)

(24)

4)计算非线性权.根据文献[94-95]中提出的类似思想，定义：

(25)

非线性权为

(26)

(27)

本小节只介绍了一维结构网格上multi-resolution WENO限制器的构造过程，二维结构网格和三角形网格上multi-resolution WENO限制器的构造过程参见文献[89,96].DG方法结合这种multi-resolution WENO限制器在求解双曲守恒律方程组时，可以在光滑区域保持DG方法的数值精度且在强间断附近有效抑制伪振荡的出现.这种新型multi-resolution WENO限制器使用的线性权可以是任意和为1的正数.这种新的WENO限制器构造非常简单且适用于任意高阶DG方法及应用于二维和三维问题的高精度数值求解.

3 总结及展望

本文综述了高精度DG方法和高精度WENO限制器的一般构造过程及其在双曲守恒律中的应用.与现有高精度限制器相比，新型WENO限制器在以下几个方面独具创新：可以在多维(一维、二维以及三维)情况下保持物理量的守恒性和计算格式的鲁棒性，在解的光滑区域不会因限制器的原因导致计算精度下降，同时在强激波或接触间断区域保持本质无振荡性质；在解的光滑区域依然保持高阶数值精度的同时间断过渡区域更为狭窄，能显著提高激波分辨率；很好地保持了DG方法的空间紧致特性，对DG方法在求解定常可压缩流体问题的收敛性和收敛速度有较大改进；易于在非结构网格、混合网格、运动网格、自适应网格等复杂网格体系下构造和编程实现，随着计算问题的维数增加，限制器的构造和编程依然非常简单，显著降低计算机内存资源的占用进而显著提高计算效率.截至目前，新型WENO限制器是已发表相关文献中空间最紧致、鲁棒性最高、编程实现最为简便的一类高精度非线性限制器.该类限制器具有较强的通用性，能在结构网格、非结构网格、杂交网格、运动网格、自适应网格等情况下灵活使用且对网格质量要求较低，且能够推广至任一紧致类格式，如重构校正方法(CPR)/通量重构(FR)格式、谱差分(SD)/谱体积(SV)方法等，因此具有较广泛的军事和商业工程应用前景.