Banach空间中的超弱紧集合
2021-04-17程立新程庆进
程立新,程庆进
(厦门大学数学科学学院,福建 厦门 361005)
1 预备知识
众所周知,紧集是拓扑空间中重要的基本概念之一.如果考虑的拓扑空间是赋范线性空间,那么它的闭单位球是紧集的(即每个序列都有一个收敛子列)充分必要条件是这个线性空间为有限维.对于一般Banach空间而言,它的紧集只能“几乎”包含在有限维子空间之中,这个集类小到几乎可以忽略不计.此时,人们往往考虑用“弱紧性”来代替紧性.这样它不仅可以保证一大类Banach空间——自反空间的每个有界集是相对弱紧的(即每个序列都有一个在弱拓扑意义下的收敛子列),这一概念还广泛适用于一般的(无穷维)Banach空间.因此,弱紧集这一概念可以理解为自反空间的局部化.进入20世纪70年代,James[1]、Enflo[2]和Pisier[3]等著名泛函分析学家对自反空间的研究发现,有一类性质更好的Banach空间——超自反空间,除了具有自反性之外,还有很好的拓扑性质以及在再赋范的意义下具有几乎可以和Hilbert空间媲美的几何性质.同时,这类空间并不“小众”.例如,这类空间包括了最经典而常用的Banach空间lp,Lp(1 Banach空间中的弱紧集理论已经形成了一套相对完善的理论体系并在数学各分支中具有极其重要的应用[11-12].超自反空间是通过有限维子空间的有限表示定义的,即一个Banach空间E被称为超自反的,如果每个在E中有限表示的空间是自反的.自James[1]在1972年引入超自反空间的概念后,这类空间的研究便备受关注,在短短几年间,泛函分析学家们就建立了此类空间的一些奠基性结果.例如:1972年James[1]证明了一个Banach空间E为超自反当且仅当其闭单位球BE不含有任意有限枝的树;同年,Enflo[2]利用James树特征定理,构造性地证明了每个超自反空间均可再赋范成一致凸空间;1975年Pisier[3]进一步利用Banach空间值的鞅,从概率角度证明了每个超自反空间均可再赋范成一个具有指数型凸性模的一致凸空间.Enflo-Pisier再赋范定理被认为是再赋范理论最为经典和深刻的结果,是再赋范理论的里程碑.经过近50年的发展,超自反空间理论已成为一个研究内容多样、结论丰富并具有广泛应用的研究领域.然而,一个自然的问题是怎样把超自反空间这一概念局部化的?这是因为一方面为了实现理论系统的完善和完美性,需要一个正像弱紧集是自反空间的局部化;另一方面,在应用上往往要求整个空间的超自反性的假设是不必要的甚至是不可能的.遗憾的是30多年来这一个概念并没有被提出,究其原因,可能的困难点在于如何合理地将空间超自反概念中用到的“有限表示” 局部化到一般集合上. 近20年来,随着粗几何和非交换几何以及非交换群论的发展,人们发现超自反空间与粗几何领域中一些亟待解决的重要问题(例如粗Novikov猜测)密切相关[13-17],并产生了许多新的有趣问题.例如:2006年Kasparov等[13]证明了粗Novikov猜测对于可粗嵌入超自反空间的有界几何成立.但随后Lafforgue[15]和Mendel等[16]发现存在一类有界几何(膨胀图)不能粗嵌入任何的超自反空间.在此背景下,寻求使得有界几何可粗嵌入超自反空间的条件成为一个自然的问题.本文第2作者在程立新老师指导下从2004年起开始超自反空间局部化问题的研究.想法是首先将超自反这一概念局部化,即提出合理的超弱紧集概念;然后研究超弱紧集嵌入超自反空间的条件并应用到新型的粗嵌入中.主要研究这样的一类有界几何空间,它们可拉回到Banach空间单位球内形成像超自反空间中的子集那样具有某种“超性质”的集合,分析清楚它们向超自反空间的一致嵌入问题,然后应用到此类有界几何向超自反空间的粗嵌入上.2007年Cheng等[18-19]发现,利用顶点在目标集合中的“单形”来代替有限维子空间来定义集合的有限表示是“有限表示”的一个非常自然而适用的局部化概念.因此,超自反空间的局部化问题“单形”局部化了James有限表示的概念,进而对Banach空间中的有界弱闭集引入了超自反空间的一个局部化概念,即超弱紧集,并建立了平行于超自反空间中有界子集的一系列性质以及局部化的James-Enflo再赋范定理[20-21]. 后来发现很多关于Banach空间特殊集合的概念可以与超弱紧集关联起来,最早可追溯到20世纪70年代.1976年Beauzamy[22]将空间的超自反性推广到两个Banach空间之间的线性算子上,引入了“一致可凸化”(法文称“uniformément convexifiant”)算子的概念,并建立了算子版的James-Enflo定理,更多算子版的推广概念可参见文献[23-26].2008年Raja[27]通过局部化Lancien[28]的指标性质,在Banach空间中的一个有界闭凸集上定义了有限指标性质,并证明此类集合上可再赋“一致凸”范数;2009年Fabian等[29]通过局部化Lancien的对偶指标性质,在Banach空间中的一般有界子集上引入有限对偶指标性质,证明了此类集合上可再赋某种“一致M-可微”范数.2018年Cheng等[21]系统地研究了一般超弱紧集的性质,特别是发现了对一个有界闭凸集而言Raja的有限指标性质.Fabian等[29]的有限对偶指标性质和本课题组的超弱紧集这3个概念是等价的,并且一个算子T:X→Y为一致可凸化算子当且仅当TBX为Y的一个相对超弱紧集.目前,超弱紧集这一概念已被认为是超自反空间的一个合理、统一、恰当的局部化概念[30]并被广泛研究.研究表明超弱紧集广泛存在于非超自反空间环境中,这类集合很好地遗传了超自反空间的几何和拓扑性质,并与历史上一些经典的概念例如一致Eberlein紧、不动点、Banach-Saks性质、一致弱零集等有着密切的关系.最近的一些文献[21,31]表明,超弱紧集理论正成为一个活跃的研究方向. 本文简要介绍超弱紧集的研究进展,重点介绍超弱紧集的两个嵌入定理以及超弱紧凸集上的Enflo再赋范定理,最后给出尚待解决的问题. (1-ε)‖x-y‖≤‖Tx-Ty‖≤ (1+ε)‖x-y‖,∀x,y∈aff(Sn). (1) 易知Banach空间X在Banach空间Y中有限表示,当且仅当相应单位球BX在BY中有限表示. Banach空间的超幂(ultraprower)是一个用无限维方法研究有限表示的合适工具.设U为自然数集N上的一个自由超滤子,空间XU表示Banach空间X关于U的超幂空间.XU中的(等价类)元素将用[(xn)]或(xn)u表示,这里代表元(xn)∈(∑n∈N⨁X)∞.对集合A⊂X,其超幂为 xn∈A(n∈N)}. 集合的超幂与有限表示有着密切的关系[21]:设A为Banach空间X的一个非空集,U为自然数集N上的一个自由超滤子,则AU在A中有限表示.该结果在后面的研究中起到了非常关键的作用. 类似于James引入超自反空间的概念,可以自然地引入超弱紧集的定义:称Banach空间X中的一个子集A是相对超弱紧的,如果每个可在A中有限表示的Banach空间Y中的集合B是相对弱紧的,特别地,如果A还是弱闭的,此时称A为超弱紧的. 根据超弱紧集的定义有:1)一个Banach空间为超自反的当且仅当其闭单位球为超弱紧的;2)超自反空间中的每个有界集为相对超弱紧的;3)Banach空间中的每个紧集为超弱紧的.弱紧和超弱紧之间的关系可以通过如下的超幂得到[21]:A是Banach空间X的一个非空子集,则A是(相对)超弱紧的当且仅当对自然数集N上的某个自由超滤子U,有AU是(相对)弱紧的. (ii)设A⊂c0满足对每个ε>0,存在Nε∈N使得 #{n∈N:|x(n)|≥ε} 其中#B表示集合B的势.则A为相对超弱紧集. 例2对任何测度空间(Ω,μ),则L1(Ω,μ)中的每个弱紧集均为超弱紧的. 需要注意的是在c0中存在着弱紧而非超弱紧的子集[21].这表明只要K为无限紧集,则连续函数空间C(K)上总存在弱紧而非超弱紧集.这是由于c0总是线性同胚于C(K)的一个闭子空间[33].到目前为止,还没有c0中超弱紧集的特征化定理. James引入的树性质[1]是刻画超自反性的一个非常有用的几何工具,James树定理表明一个Banach空间是超自反的当且仅当其闭单位球不具有有限树性质.超弱紧集也具有James型的树特征定理:设A⊂X是一个有界集,则A是相对超弱紧的当且仅当A不具有有限树性质. 弱紧集的Grothendieck定理表明Banach空间X的一个子集A是相对弱紧的,当且仅当对每个ε>0存在一个相对弱紧集B使得A⊂B+εBX.这一准则对超弱紧集仍然成立[21]:Banach空间X的一个子集A是相对超弱紧的,当且仅当对每个ε>0存在一个相对超弱紧集B使得A⊂B+εBX.这一准则也是判定一个集合为超弱紧的一个有用工具. 前面的结果表明判定一个集合A的超弱紧性可通过A的超幂AU的弱紧性来反映,而著名的James定理表明,AU的弱紧性可由超幂的对偶空间(XU)*中的泛函在AU上的上确界的可达性来刻画.但对一个非超自反空间X而言,它的超幂的对偶空间(XU)*要严格的大于(X*)U,这意味着(XU)*中存在许多未知或者不可表示的元素,这给利用James定理来研究AU的弱紧性带来了很大困难.然而,James对弱紧性给出了一个纯粹从自身出发的序列特征刻画[34],Cheng等[21]证明了超弱紧性也具有类似的James型序列特征,这对于超弱紧集的刻画是极其有用的:设A是Banach空间X中的一个 子集,则A不是相对超弱紧的当且仅当A具有一致有限的可分离性质,即存在θ>0使得对每个n∈N,可找到{x1,x2,…,xn}⊂A满足 dist(co{x1,…,xj}, co{xj+1,…,xn})≥θ,(∀1≤ j 上面提供的超弱紧性的3类特征,再加上相对超弱紧性对有界线性算子的保持性,是判定一个集合为超弱紧的重要依据. Banach空间的局部嵌入问题早在20世纪70年代就引起了人们的关注,最具代表性的结果是Davis-Figiel-Johnson-Pelczynski嵌入定理[35]:Banach空间中的每个弱紧集均可线性弱嵌入进某个自反Banach空间.这一结果直接来自于著名的Davis-Figiel-Johnson-Pelczynski插值引理[35],2007年本课题组[18-20]发现此引理中弱紧集的弱嵌入可以改进为强嵌入:Banach空间中的每个弱紧集均可线性一致嵌入某个自反Banach空间[36]. 对比弱紧集合的嵌入,一个自然的问题是每个超弱紧集是否可线性嵌入某个超自反空间?遗憾的是,答案是否定的.事实上从超弱紧凸集出发,按照Davis-Figiel-Johnson-Pelczynski插值引理产生的自反Banach空间Y—般不再是超自反的.特别地,2016年Raja[30]举出反例表明存在超弱紧集不能线性弱嵌入进任何超自反Banach空间. 利用Enflo构造一致凸范数的技术以及联合超弱紧集的Grothendieck型定理和本课题组修改版的Davis-Figiel-Johnson-Pelczynski引理,得到每个超弱紧集可线性一致嵌入某个自反且相对一致凸空间[18-20].设K是Banach空间(X,‖·‖)的一个超弱紧凸集,则存在自反Banach空间(Y,|·|)使得: (i)K⊂B(Y,|·|)⊂X. 2(|xn|2+|yn|2)-|xn+yn|2→0, 那么‖xn-yn‖→0. (iii)限制在集合K上,范数|·|和‖·‖生成的拓扑是一致的.特别地,(K,|·|)是一致凸的. 如果将线性嵌入减弱为非线性嵌入,则可获得超弱紧集的弱嵌入定理,这特别给出了一致Eberlein紧的拓扑刻画.回顾相关事实,1968年Amir等[37]引入了Eberlein紧的概念:一个紧Hausdorff空间K被称为是Eberlein紧的,如果K拓扑同胚于一个Banach空间中的一个弱紧集(在弱拓扑意义下).著名的Amir-Lindenstrauss结构定理[37]表明:一个Hausdorff拓扑空间K为Eberlein紧的,当且仅当存在某个指标集Γ使得K同胚于c0(Γ)中的某个弱紧集. 他们也举出了Banach空间中存在弱紧集为Eberlein紧而非一致Eberlein紧的例子.更多一致Eberlein紧的研究可参见文献[39-41].对比Eberlein紧和弱紧集的关系,自然的问题是研究一致Eberlein紧与超弱紧集的关系.对此问题,首先在2008年,Raja利用Davis-Figiel-Johnson-Pelczynski定理[35]及Fabian等[40]关于Banach空间对偶单位球为一致Eberlein紧的特征定理,证明了每个具有有限指标性质的有界闭凸集(也就是现在的超弱紧凸集)为一致Eberlein紧的;这再联合本课题组[32]证明的超弱紧集合的闭凸包仍为超弱紧的以及Benyamini等[37]的结果,便得到超弱紧集的弱嵌入定理:每个超弱紧集都可以弱嵌入某个超自反空间(或等价的,弱嵌入某个Hilbert空间). 现在考虑凸的超弱紧集.研究表明在凸集的情况下,超弱紧集具有更好的几何和拓扑性质.此时,凸的超弱紧集继承了超自反空间那些涉及“良好”范数和“良好”凸函数等存在性的更加深刻的性质,例如凸的超弱紧集上的Enflo再赋范定理成立,这一结果是超弱紧集理论的核心结果之一,以此结果为基础,可进一步产生凸的超弱紧集的指标特征等结果;此外,有例子表明,有些超弱紧的性质中凸性是必要的假设条件[42]. James[1]在1972年证明了每个一致凸空间是超自反的;反之,Enflo[2]证明了每个超自反空间X均可找到一个等价范数|·|使(X,|·|)为一致凸空间(此时称X可一致凸化).随后在1975年,Pisier[3]将Enflo的再赋范定理改进为定量化的结果.自20世纪70年代开始,人们从各种不同的角度出发去推广和局部化Enflo和Pisier再赋范定理.例如1976年Beauzamy[22]引入了一致可凸化算子的概念并建立了算子版的James-Enflo再赋范结果,但Pisier[3]指出一致可凸化算子不一定可再赋指数型凸性模;1995年Lancien[28]利用Banach空间单位球及其对偶单位球的Szlenk指标和弱Szlenk指标给出了Pisier再赋范定理的一个简单而且是几何途径的证明. 2007年Cheng等[20]从超弱紧凸集不具有有限树性质出发,充分利用Enflo构造一致凸范数的技术以及超弱紧集的强嵌入定理,得到了 James-Enflo再赋范定理的局部版:设K为Banach空间X的一个有界闭凸集,则K为超弱紧的(当)且仅当存在X上的一个等价范数|·|使得(K,|·|)是一致凸的,也就是如果xn,yn∈K满足 2(|xn|2+|yn|2)-|xn+yn|2→0, 那么|xn-yn|→0. 受Lancien指标途径的再赋范结果启发,Raja[27]和Fabian等[29]将Lancien的指标性质局部化到一般集合上,并建立了Enflo形式的再赋范结果: 1)设K是Banach空间X的一个有界闭凸集合,如果K具有有限指标,那么在X上存在一个等价范数|·|使得(K,|·|)是一致凸的;2)如果有界闭凸集K具有有限指标性质,那么在X上存在一个等价范数|·|使得(K,|·|)是一致Gateaux光滑的. 利用关于超弱紧凸集上的再赋范结果,可以证明对于凸集而言,Raja[27]引入的有限指标性质和Fabian等[29]引入的有限对偶指标性质与超弱紧集的概念是等价的.因此超弱紧凸集的等价特征为:设K为Banach空间X中的一个有界闭凸集,则以下条件等价[20-21,27,43-44]: 1)K为超弱紧集;2)K具有有限指标性质;3)K具有有限对偶指标性质;4)K不具有有限树性质;5)K可再赋范具有一致凸性;6)K具有Δ-凸函数逼近性质;7)K不具有一致有限双正交性质;8)K具有超Banach-Saks性质;9)K可再赋范具有M-一致Gateaux光滑性;10)K对仿射等距具有超不动点性质. 1)是否每个超弱紧集可一致嵌入某个超自反空间或者Hilbert空间? 2)如果由有界几何生成的超弱紧集可一致嵌入某个超自反空间或者Hilbert空间,那么是否蕴含了有界几何本身可粗嵌入某个超自反空间或者Hilbert空间? 注意上面问题1)中,如果超弱紧集为内部不空的,例如为超自反空间的单位球时,其是否可一致嵌入某个Hilbert空间是Banach空间理论中的一个长期的公开问题[45].最近Cheng等[42]研究了超弱紧凸集上的绝对一致收缩,Lancien等[31]建立了超弱紧集上的Bourgain、Johnson和Schechtman型的度量特征. 最后需要指出问题2)是本课题组引入超弱紧集的最初的动机之一,目前尽管超弱紧集理论的框架已基本构成,但超弱紧集的一致嵌入问题及其在粗几何中的应用(特别是问题2))至今还没有好的结果,问题1)和问题2)将是本课题组以后关注和研究的问题. 致谢:感谢厦门大学泛函分析团队的探讨和支持!2 超弱紧集的定义和基本性质
2.1 集合的有限表示和超幂
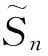
2.2 超弱紧集的基本性质
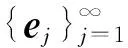
2.3 超弱紧集的特征
3 超弱紧集的嵌入
3.1 线性嵌入
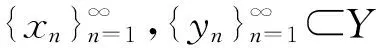
3.2 非线性嵌入
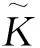
3.3 超弱紧凸集上的Enflo再赋范定理
4 尚待解决的问题
