核心素养视角下的“基本不等式”教学设计

龚景昱

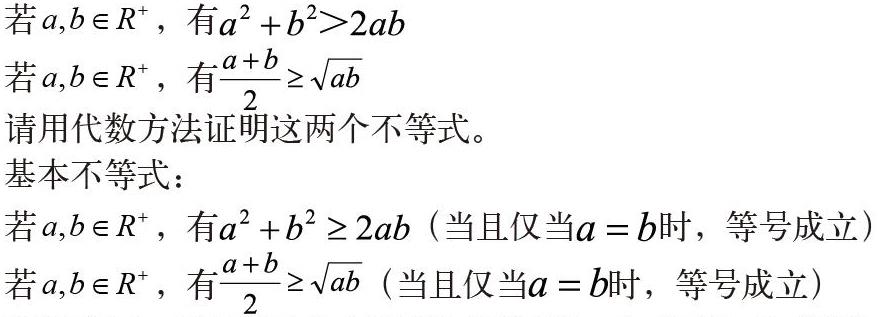
摘 要：“基本不等式”属于高中数学基本预备知识，对培养学生数学解题策略也有关键作用。当前数学教育关注学生数学学科核心素养，尤其强调数学抽象、数学建模素养，这些方面在本文给出的教学设计中得以体现。

关键词：核心素养 基本不等式

本文给出核心素养视角下的“基本不等式”教学设计。

1 教学设计

1.1 问题情境，导入新知

一个顾客发现自己购买金饰重量和老板标的不一样，于是向金店的老板要求赔偿，老板提出了解决方案：把金饰在天平两侧重量的平均值作为实际重量。

问题1：如果你是这个顾客，你接受这个方案吗？说说原因。

问题2：解决方案是否转化成了和谁大的问题？能估计一下它们的大小关系吗？

设计意图：使学生对不等关系有初步猜测，鼓励学生独立思考。

1.2 动手操作，几何引入

探究一：如图是我国古代数学家赵爽的“弦图”，你能找出一些不等关系吗？

探究二：把两张正方形纸片沿对角线折成两个等腰直角三角形，用这两个三角形拼接出一个矩形。设两个正方形的面积分别为a和b，比较两个直角三角形的面积和拼出的矩形的面积，这其中存在什么不等关系？

设计意图：通过观察几何图形和动手操作，使学生对基本不等式中大小关系有直观体会，为后面严谨证明提供前提和铺垫。

1.3 代数证明，得出结论

由两个探究，初步形成两个不等式结论：

请用代数方法证明这两个不等式。

基本不等式：

设计意图：引导学生使用进行严谨证明，由“形”到“数”，更加深刻理解基本不等式的内涵。

1.4 几何证明，相得益彰

探究三：如图为圆的直径，点C是AB上一点，AC=a，BC=b，过C作垂直于AB的弦DE，连接AD，BD。

设计意图：进一步加强数形结合的意识，让学生体会以数代形，通过对图形的观察分析以形代数，进而完善前面的代数结论。[2]

1.5 应用举例，建立模型

例1.（1）用篱笆围100平方米的矩形菜园，菜园的长、宽各为多少时，所用篱笆最短，最短的篱笆是多少？

（2）一段36米的篱笆围矩形菜园，菜园的长、宽为多少时，菜园的面积最大，最大面积是多少？

设计意图：学生自己归纳出利用基本不等式求最值问题的数学模型，体会不等式在现实中的应用。

例2.求的值域

设计意图：在巩固运用所学知识解题的基础上，体会数形结合的思想。引导学生理解基本不等式的三个限制条件在解决最值问题中的作用，体会数学方法与解题策略。

1.6 归纳小结，反思提高

（1）本节课学习了基本不等式的两种形式，还有哪些变式？

（2）你能总结一下如何运用基本不等式解决简单最值问题吗？

设计意图：通过提问帮助学生建立知识体系，理解数学基本思想方法。

2 教学设计反思

2.1 重视创设合适的数学教学情境

通过情境，建立数学学习和实际生活的联系，是培养学生数学素养的有效策略。好的情境，数学知識和方法蕴含于其中，学生通过认识情境而获得知识，在这个过程中自然而然获得从情境到数学知识的转化。本文中的教学设计在导入部分采用天平问题的数学教学情境，从提出问题指向不等关系，再从不等关系抽象到不等式，为后续的几何探究奠定基础。

2.2 关注学生思维过程

本文的教学设计，从天平问题出发引出两种几何探究情境。尽管两种几何情境得到的初步结论不够完善，也不妨碍学生自主进行代数证明，证明结果和原命题产生冲突，激发他们的探究热情，这个过程是体现了“由形到数”。让学生证不完善的命题，引起他们的认知冲突，这更符合学生思维特点，一定程度上经历了“自我纠错”的过程，培养了学生的严谨思维能力。运用代数法证明后，再次回到几何情境，移动弦的位置更直观看出公式形成的过程，这个过程体现了“由数到形”。整个过程经历了数形结合的过程，使学生能够更深刻理解不等式成立的条件及几何意义。

2.3 帮助学生积累数学活动经验

帮助学生积累数学活动经验，就是引导学生进行观察、操作，完成问题解决和反思的过程。本文教学设计中，两处体现了基于核心素养的要求，动手操作、归纳模型属于两种典型的数学活动经验。几何探究部分，通过观察几何图形和动手操作，使学生对基本不等式的形式有直观体会，为严谨证明提供前提。应用举例部分，通过两个典型问题引导学生建立求最值的数学模型，体现了核心素养中所强调的数学抽象和数学建模素养。

参考文献：

[1] 教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018.

[2] 蔡涛.立足素养 精准教学——新教材“基本不等式”第一节的教学实践与感悟[J].数学通讯，2020（20）：26-29.

南京师范大学 （江苏省南京市 210000）