高考数学文化考查特征研究——基于2020年高考试题的统计分析*

谢发超 (四川省成都市玉林中学 610041)

1 引言

2020年1月，教育部考试中心发布的以“一核四层四翼”为基本内涵的《中国高考评价体系》成为新时代高考内容改革的理论支撑和实践指南．根据学科功能定位，数学科确定了考查理性思维、数学应用、数学探索和数学文化4类学科素养和逻辑思维能力、运算求解能力、空间想象能力、数学建模能力和创新能力5种关键能力．[1]作为《普通高中数学课程标准(2017年版)》(下称《课标2017》)中的重要课程内容，数学文化在高考中的考查路径、考查方式和考查水平已成为广大数学教育工作者关注的焦点．本文拟就2020年高考数学试题对数学文化的考查情况进行统计，分析高考数学文化考查的内容、类型、方式及认知水平，以期对数学文化试题命制和数学文化素养培育提供些许启示．

2 研究方法

2.1 分析框架

首先，数学文化的内涵与分类尚无明确统一的认识．《课标2017》指出：“数学文化是指数学的思想、精神、语言、方法、观点，以及它们的形成和发展；还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动．”[2]汪晓勤将数学文化分为数学史、数学与生活、数学与科学、数学与人文、数学与艺术、趣味数学6类[3]．王建磐等则将其分为数学史、数学与现实生活、数学与科学技术、数学与人文艺术等4类[4]． 张维忠等将高考试题中的数学文化内容类型分为数学史、数学与生活、数学与科技、数学与人文艺术4类[5]．结合上述观点，本文将高考试题中的数学文化根据其与数学的关联分为数学史、社会生活、人文艺术、科技创新和数学游戏等5类．

其次，从知识体系角度看，《课标2017》与《普通高中数学课程标准(实验版)》、《中国高考评价体系》和《2019 年全国卷高考数学考试大纲》之间具有充分的传承性和较大的相似性．同时，虽然高考数学的知识体系与课程标准中的知识体系总体上一致，但高考数学对这些知识点进行了有机的整合，使得在必备知识中不同主题、不同知识点等均呈现出了科学的逻辑关系．结合上述理解，本文将高考数学内容分为“集合与逻辑”“函数与导数”“几何与代数”“算法与框图”“概率与统计”五个内容领域．

最后，根据布鲁姆教育目标分类学(2001年修订版)，将认知过程分为记忆、理解、应用、分析、评价、创造6个水平要素及19个亚类(表1)，其中前四个水平为低阶思维水平，后两者为高阶思维水平．利用亚类中的动词可以推断目标所对应的认知水平．

表1 认知过程维度分类

2.2 数据处理

将2020年教育部考试中心命制的8套数学试卷，包括文理科全国Ⅰ、Ⅱ、Ⅲ卷，供山东省使用的不分文理科的新课标Ⅰ卷，供海南省使用的不分文理科的新课标Ⅱ卷，以及各省市自主命制的不分文理科的北京卷、上海卷、天津卷、浙江卷和江苏卷共13套试卷纳入分析对象．统计过程中，以题号为单位，若一道试题包含若干小题，仍计为一道题．若文理科均有，只计为一道题．同一数学文化元素出现在不同试题中分别计数，同一试题中出现不同的数学文化元素分别计数，但对试题分值进行分拆．据此，得到初步统计结果(表2)．其中新课标Ⅰ、Ⅱ卷的数学文化试题完全相同．

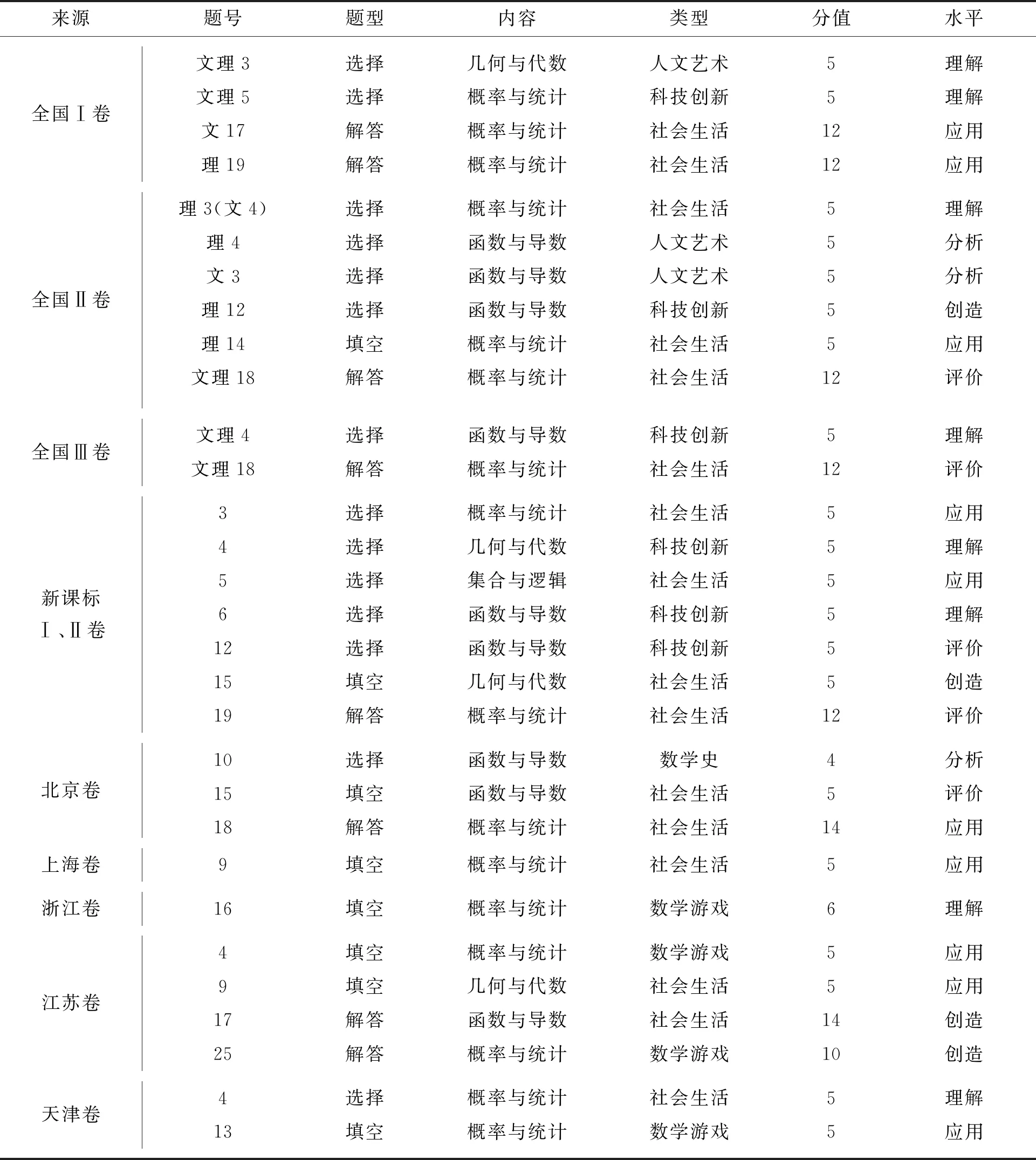
表2 数学文化考查初步统计

3 研究结果

3.1 考查内容

对13套试卷中数学文化试题的考查内容统计如表3．从题目数量看，在全部30道数学文化试题中，概率与统计部分有16道，占比53.33%，其次是函数与导数部分有9道，占比30.00%，而算法与框图部分则没有试题涉及．从题目分值看，数学文化试题共计208分，其中概率与统计占130分，占比62.50%，其次是函数与导数部分占53分，占比25.48%．

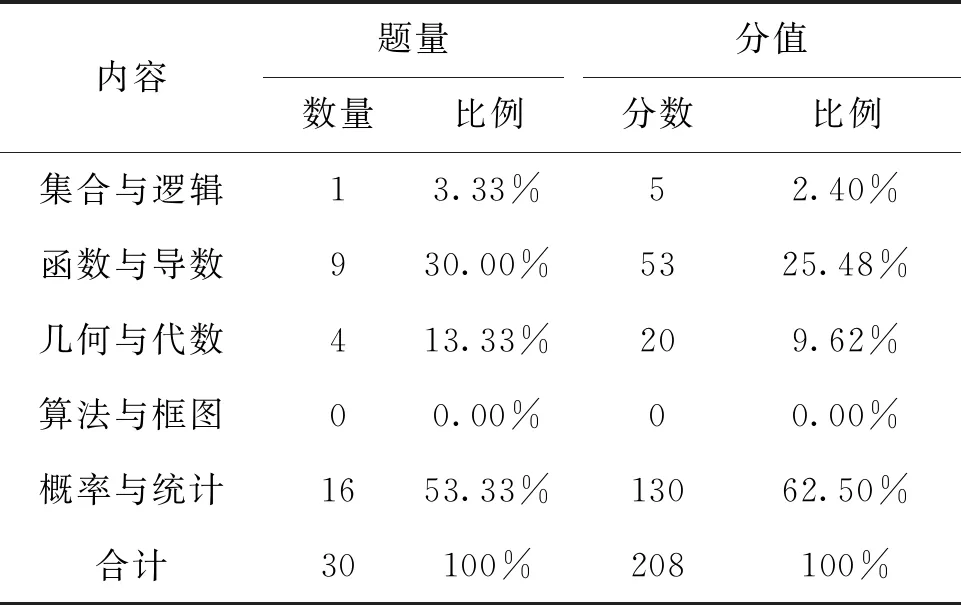
表3 数学文化考查内容统计

从考查内容分析高考数学文化试题，可以在一定程度上认识高考改革关切的主干知识与数学文化学科素养的契合情况，有助于引导中学数学教师明确应该在哪些地方强化数学文化的教育．在《课标2017》中已经弱化或者删除的部分，自然不会再作为重要考查内容，如算法与框图、线性规划、三视图等．而对于概率与统计部分，则因依据大量无组织的信息进行数据分析处理，并作出合理的决策，这已成为未来公民必备的基本核心素养[6]，同时，概率与统计的学习可帮助学生掌握数据收集、整理和表示的方法，体会统计思维与确定性思维的差异、归纳推断与演绎证明的差异，自然会重点考查数学文化．此外，在函数与导数内容中也蕴含着丰富的数学文化内容，如映射与函数的概念、导数的物理学背景、常见的函数模型及应用等，都是很好的数学文化试题命制点．

3.2 考查方式

对13套试卷中数学文化试题的呈现方式统计如表4．可以发现，30道题目中有22道题以选择题、填空题的形式出现，占比73.33%，其分值达110分，占比52.88%．这些数据表明，在数学文化考查方式上，更多地发挥了选择、填空题行文简洁凝练，考查目标集中，答案简短、明确、具体，评分客观、公正、准确等特点．同时，除了上海、浙江、天津三省市外，其余高考卷中都至少有一道题以解答题形式考查数学文化．

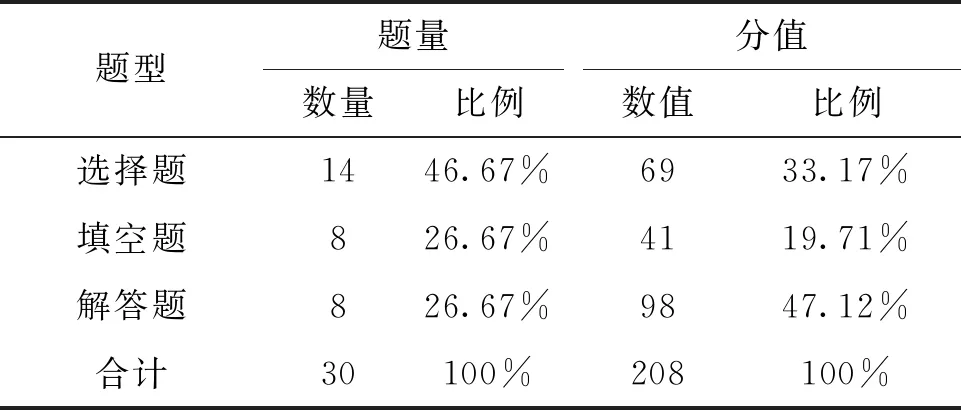
表4 数学文化试题呈现方式统计

3.3 考查类型

对13套试卷中数学文化试题的考查类型统计如表5．从表5可以发现，在试题数量上，社会生活类的数学文化试题为16道，占比53.33%，其次是科技创新类的数学文化试题有6道，占比20.00%．从题目分值看，社会生活类试题占133分，占比63.94%，其次是科技创新和数学游戏类，分别为30分和26分，占比14.42%和12.50%．

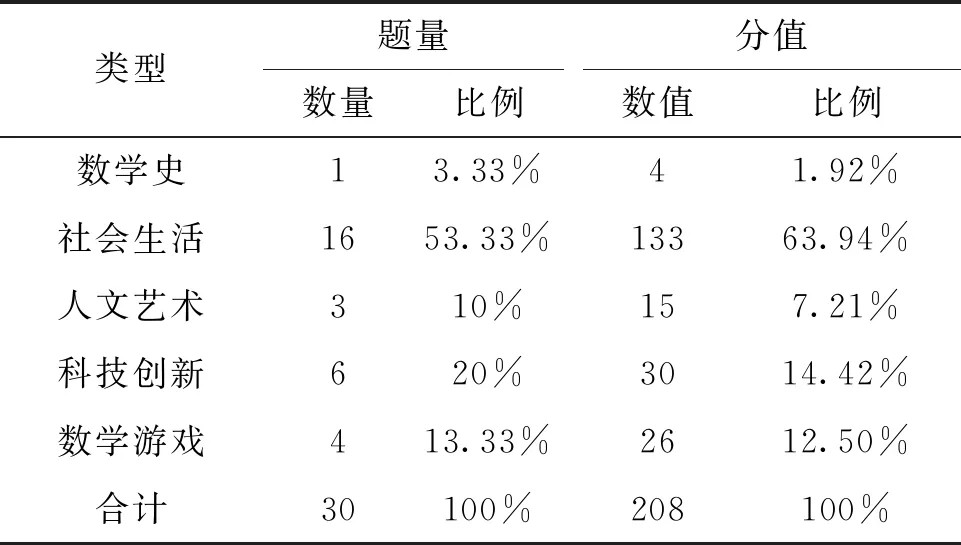
表5 数学文化试题考查类型统计

由此可知，在更加强调培养学生“四基”“四能”“三会”“六素养”的数学课程改革背景下，高考命题将按照“四翼”的要求，“强调学以致用，将抽象的数学概念与实际生活相结合，运用数学知识、思想和方法对实际问题进行分析与研究，进而解决问题，通过联系生产生活实际的试题情境设计，考查学生有效解决实际问题的方法和能力．”[1]13套试卷中社会生活、科技创新两类数学文化试题共22道，占比73.33%，分值和为163分，占比78.36%．尤其在新课标I、II卷中，一套试卷有6道题是考查社会生活、科技创新类的数学文化试题，分值占全卷的24.67%．但这其中有两个问题：一是以人员安排、体育比赛等为背景的试题较多，以科技创新为背景的试题偏少；二是对数学史给予的关注度不够．所有试题中只有北京卷第10题考查了波斯数学家、天文学家阿尔·卡西利用正多边形逼近圆周的方法求解圆周率．

3.4 考查水平

对13套试卷数学文化试题的考查水平统计如表6．从表6可以发现，在记忆层面没有题目考查；在理解、应用、分析三个考查水平上考查试题分别为8道、10道和3道，占比为26.67%,33.33%和10%，其分值分别为41分、73分和14分，占比19.71%,35.10%和6.73%．合计在低阶思维水平考查题目数为21道，占比70%，分值为128分，占比61.54%；相应地，在评价、创造等高阶思维水平考查了9道题，占比30%，分值为80分，占比38.46%．

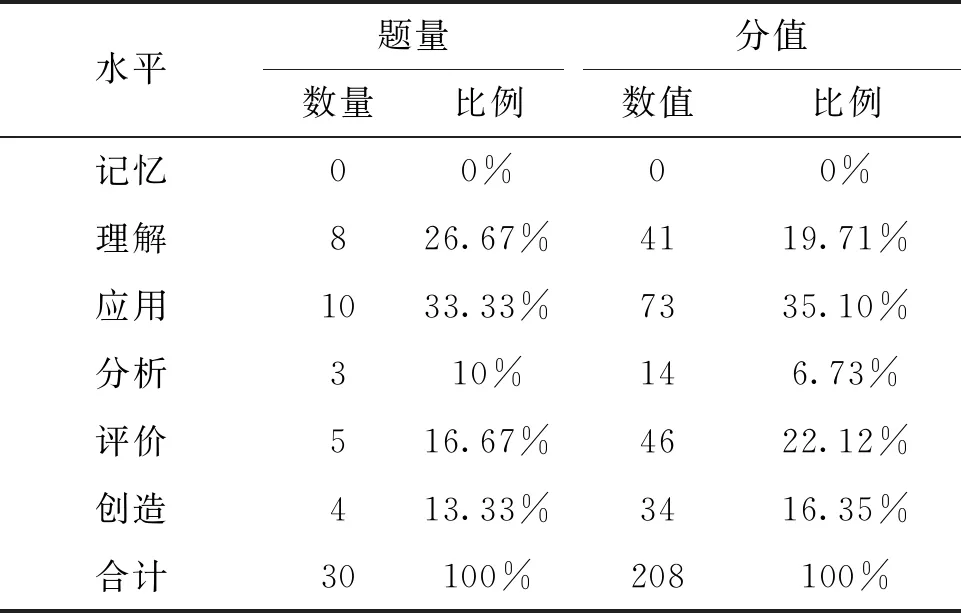
表6 数学文化试题考查水平统计

从考查水平分析高考数学文化试题，可以在一定程度上认识高考命题中数学文化学科素养的能力层级要求，有助于引导中学数学教师明确实际教学中不同类型的数学文化素养应该达到什么样的认知水平．从以上数据可以看出，2020年的30道数学文化试题既体现出对学生关键能力水平的基础性、共同性的考查，如理解、应用等，有利于对大部分学生进行层次区分，又体现出对学生关键能力发展性、特殊性的考查，如评价、创造等，有利于实现高考试卷的选拔功能．

4 结论与建议

4.1 结论

通过对2020年13套高考试卷数学文化试题的考查内容、考查方式、考查类型和考查水平的统计与分析，可以得出以下结论：

第一，数学文化试题总体水平较高．数学文化试题围绕“立德树人”根本任务，以多样的数学文化素材和丰富的数学情境关联多维数学知识，考查学生必备知识掌握情况和数学素养习得情况．这些试题以立德树人为价值取向，从德智体美劳等方面选择命题素材，不断唤醒学生对“真善美”的认识、理解和尊重，促进学生科学文化素养、人文和审美素养的提升．

第二，数学文化试题内容丰富，类型多样．数学文化试题充分反映新课改的理念和精神，在重点内容、主干知识中考查，在社会生活、科技创新背景中考查，尤其对学生信息整理能力、知识获取能力、理解探究能力考查充分.这对提高学生数学学习兴趣、培养学生探究未知的精神有着积极的引导作用．

第三，数学文化试题认知水平切合高考选拔需要．按照“一核四层四翼”基本要求，试题兼顾了基础性、综合性、应用性和创新性的要求，理解、应用、分析等低阶思维水平试题和评价、创造等高阶思维水平试题基本符合6∶4的要求，符合高考数学科整体的立意与目的．

4.2 建议

对于试题命制者，建议关注以下两个问题．其一，在凸显数学与社会生活关联的同时，需要关注中外数学史等数学传统文化对学生的教育价值，需要关注数学文化在人文艺术方面的应用，需要关注数学文化与科技创新之间的联系，从而以更为丰富的数学文化内容和更为多样的数学文化类型彰显数学文化素养的价值意义．其二，需进一步创新数学文化试题的素材选择及其融入方式，以真实自然的文化材料、体现本质的试题内容、新颖别致的呈现方式考查学生的数学文化素养．

中学数学教师应重视以下三个问题．其一，提升自己的数学文化修养．教师的专业化发展是一个永恒的过程．在核心素养为导向的新一轮课程改革中，中学数学教师要不断学习，夯实数学文化基础，注重数学文化教学，学会数学文化试题命制．其二，加强数学文化校本课程的建设．课程是学生学校生活的总和，也是教育目标的实现途径．中学数学教师要根据学校具体实际，以学生的关键能力培养、必备品格养成为目标，以国家数学课程为基础进行拓展，边实践边总结，构建富有学校特色的数学文化专题课程集群．其三，强化日常数学教学中对数学文化的渗透．作为一种学科素养，数学文化的形成不可能一蹴而就．教学中要注重数学史的引入，充分揭示知识的发生发展过程，加强数学与其他学科及生活的联系，以多种形式展示数学的美，让学生在数学文化的熏陶中逐步形成良好的数学素养．