一类四阶偏微分多智能体系统的一致性控制

陈振杰,傅勤,郁鹏飞,张丹

(苏州科技大学数学科学学院,江苏 苏州215009)

1.引言

在实际工程中,许多现象需要用偏微分方程来刻画,如波动、热传导等物理问题,由偏微分方程构建而成的系统称为分布参数系统.近年来,分布参数系统的控制设计已经应用于许多领域中,并取得了较多的研究成果[1−6].至今,关于分布参数系统的控制设计,有两种常用方法：一种是边界控制[1−3],另一种是分布式控制[4−6].本文关注的是分布式控制问题.文[4-6]借助于Lyapunov泛函方法,分析研究了二阶分布参数系统的分布式控制问题;文[7-9]则利用算子理论方法将偏微分方程转化为Hilbert空间中的常微分方程,由此解决了二阶分布参数系统的分布式控制问题.上述两种分布式控制的目的都是通过设计反馈控制器,使闭环系统的状态随着时间的增加于合适的Sobolev空间中收敛到零.相应于算子理论方法,Lyapunov泛函方法得到的结果具有应用方便、精确有效的特点[10].

近年来,随着计算机通讯技术、网络和工业的发展,多智能体系统的协调控制已被广泛应用于各种领域中,并取得了大量的研究成果[11−16].总体而言,多智能体系统可分为两类：无领导者的系统[11−13]和有领导者的系统[14−16].对于无领导者的多智能体系统,一致性问题是其协调控制研究中的一个基础性课题[11−13],它考虑的是如何设计分布式控制协议,使得所有智能体随着时间的增长能收敛到一个共同的值上,详见文[17].至今,有关一致性控制,研究关注的多智能体系统主要是由常微分方程构建而成的系统[11−13],而较少涉及到由偏微分方程构建而成的系统.最近,基于Lyapunov泛函方法,文[18]提出并研究了偏微分多智能体系统的一致性控制问题,该类系统是由两类常见的偏微分方程（热方程和二阶波动方程）构建而成.基于文[13]中的虚拟领导者方法,构建得到分布式反馈控制律.当该反馈控制律作用于系统时,系统状态的一致性误差能于合适的Sobolev空间中收敛到零.文[18]于结论处提出了可进一步研究的问题：高阶偏微分多智能体系统的一致性控制设计.

四阶波动方程来源于梁和薄板的振动[19−20],具有重要的研究意义,近年来引起了广泛的关注[21−22].至今,几乎所有的相关研究工作均关注于方程的适定性和求解问题[21−22].文[21]利用Adomian方法研究了一类变系数四阶梁方程的求解问题,借助于广义傅立叶级数展开方法,通过构建正交基函数,由此求得用基函数描述的解析解的表达式,解决了该方程解的存在性问题.

本文利用文[21]中的四阶梁方程,构建得到相应的四阶偏微分多智能体系统,并进一步研究该类系统的一致性控制问题.通过构建合适空间上的Lyapunov泛函(不同于文[18]中的),得到一致性反馈控制律.当该反馈控制律作用于系统时,状态变量的一致性误差于L2(0,l)×L2(0,l)空间内收敛到零.

2.问题描述

本文中,我们采用下列符号约定.In表示n×n单位阵,1n表示所有分量均为1的n维列向量.对给定的向量Y ∈Rm或矩阵Y ∈Rm×m,用YT表示其转置.如果Y ∈Rm×m是非奇异的,则用Y −1表示其逆矩阵.对于一个函数x(ς)∈L2(0,l),记为其范数.

图常可被用来描述多智能体系统中不同智能体之间的通讯关联,由此,图论中的一些基本概念给出如下.记G= (V,E,A)为一个带权的有向图,其结点集合为V={1,2,··· ,N},边集合为E ⊆V ×V.在图G中,用第i个结点表示第i个智能体,用一条从i到j的有向边表示有序对(i,j)∈E,意味着第j个智能体能直接从第i个智能体处接受信息.用A= (aij)∈RN×N表示图G带权的邻接矩阵,若(j,i)∈E,则aij >0;否则aij= 0.进一步,设aii= 0.定义有向图G的Laplacian矩阵为LG=D −A,这里D= diag(degin(1),degin(2),··· ,degin(N)),而表示第i个结点的入度.

引理2.1[12]Laplacian矩阵LG至少有一个以1N为特征向量的零特征值,且LG所有的非零特征值均有正实部.LG具有单重零特征值的充要条件是图G含有生成树.

记

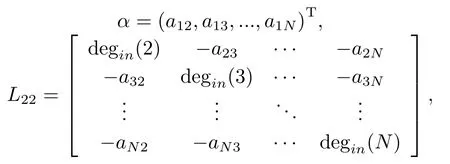
并取

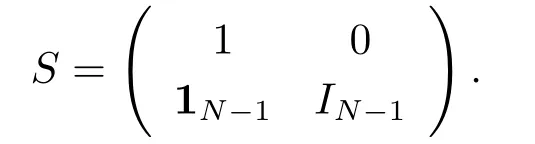
由Laplacian矩阵LG的定义,可得

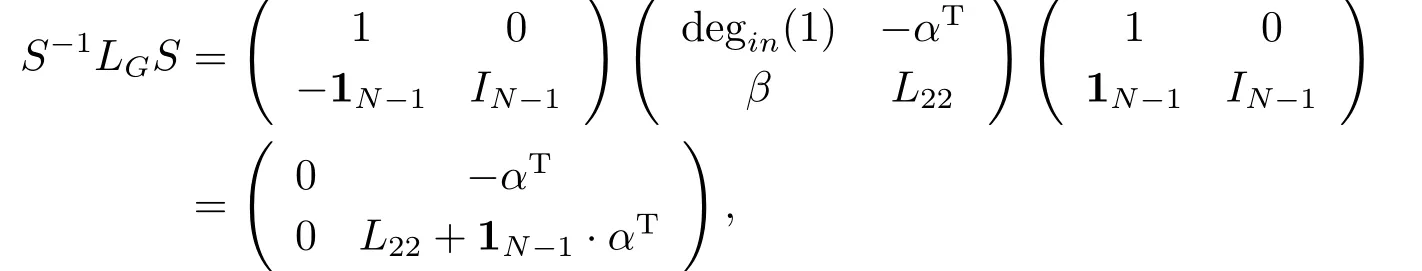
这里β=(a21,a31,··· ,aN1)T.由此,结合引理2.1,可得下列引理:

引理2.2[13]如果有向图G存在生成树,则矩阵L22+1N−1·αT的每个特征值均有正实部.

记B=−(L22+1N−1·αT).若L22+1N−1·αT的每个特征值都有正实部,则存在一个对称正定矩阵P ∈R(N−1)×(N−1),使得

文[21]研究了如下形式的变系数四阶梁方程:

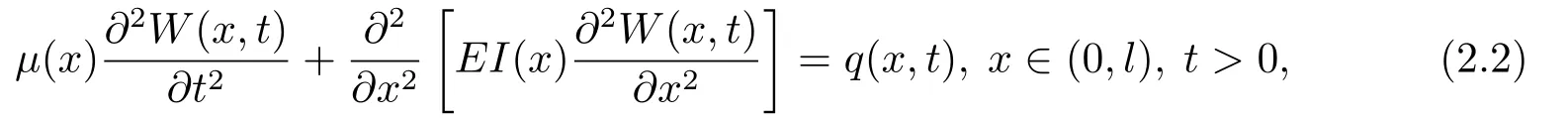
这里µ(x),W(x,t),EI(x),q(x,t)分别表示梁的单位长度质量,侧梁位移,梁抗弯刚度和单位长度荷载.

文[21]利用傅里叶级数展开式解决了方程(2.2)解的存在性问题,并给出了方程(2.2)级数形式的解,详见文[21]中公式(46).

记

由物理意义可知,µ1,µ2,EI1和EI2为正常数.

在方程(2.2)解的存在性已解决的基础上,我们用控制变量u(x,t)替换方程(2.2)中的q(x,t)(注:将单位长度荷载替换成控制变量是具有合理性的),由此得到相应的四阶分布参数系统:

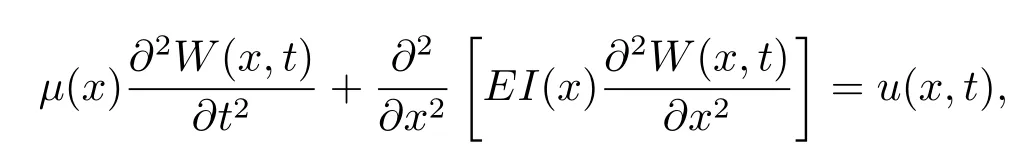
并进一步构建得到如下形式的四阶偏微分多智能体系统:

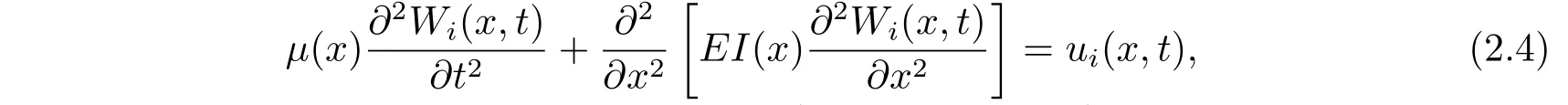
(x,t)∈(0,l)×(0,∞),i= 1,2,...,N.这里为第i个智能体的状态变量(见文[6]),ui(x,t)是第i个智能体的分布式控制输入,i=1,2,...,N.

系统(2.4)适定的边值条件如下(见文[21]):

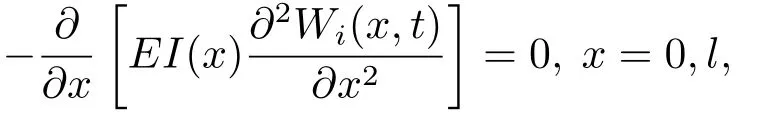
或者

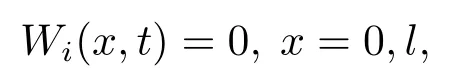
和

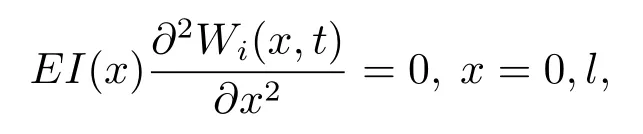
或者

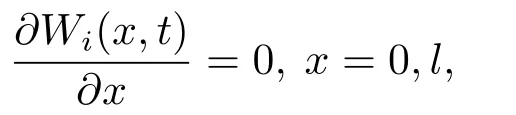
i=1,2,...,N.

假设2.1图G存在生成树.

本文的目标为:寻求系统(2.4)的分布式反馈控制律,使得状态变量的一致性误差于L2(0,l)×L2(0,l)空间内收敛到零,即

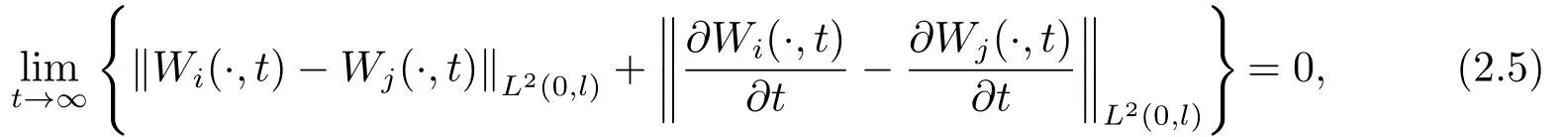
其中i,j ∈{1,2,...,N}.

3.主要结果

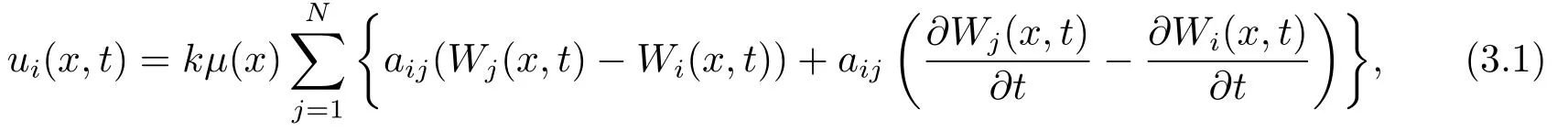
i=1,2,...,N,这里k >0为反馈增益.

记δi(x,t)=Wi(x,t)−W1(x,t),这里W1(x,t)为虚拟领导者(见文[13,18]).由此(2.5)式等价于

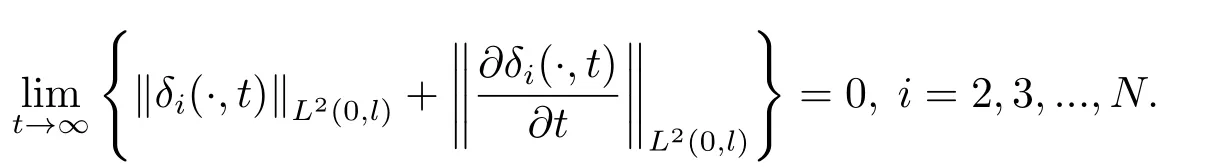
由(2.4),(3.1)式,有

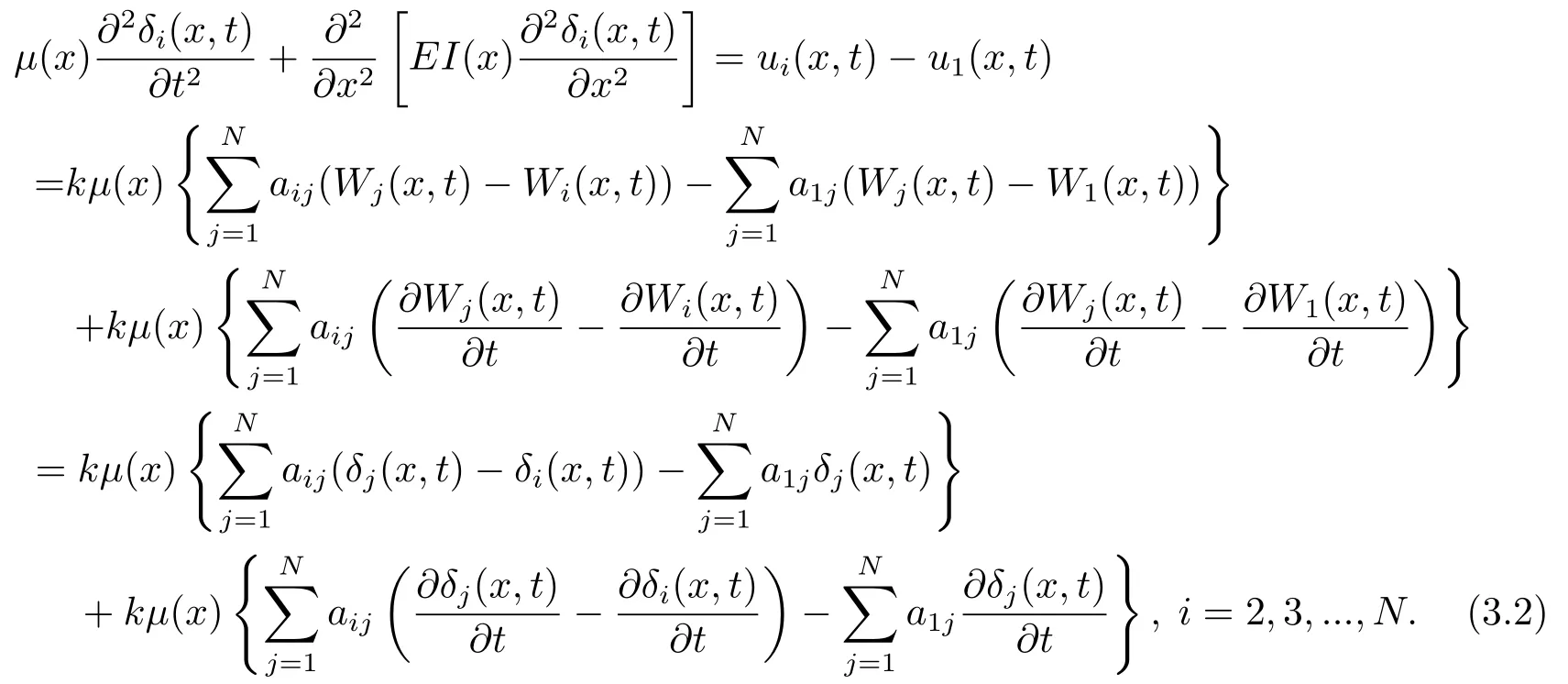
记

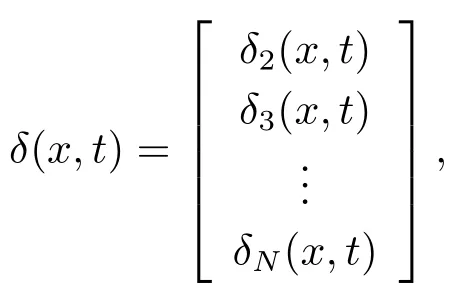
则可将(3.2)式写成如下的紧凑形式

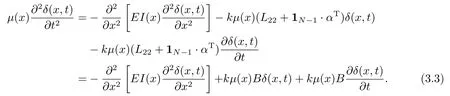
定理3.1假设2.1成立,则在反馈控制律(3.1)的作用下,系统(2.4)的一致性误差收敛到零,即(2.5)式成立,当

成立时,这里λmax(P)为矩阵P的最大特征值.

证构建如下形式的Lyapunov泛函:

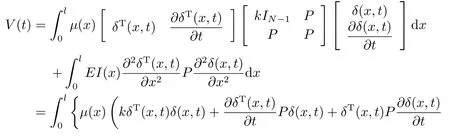
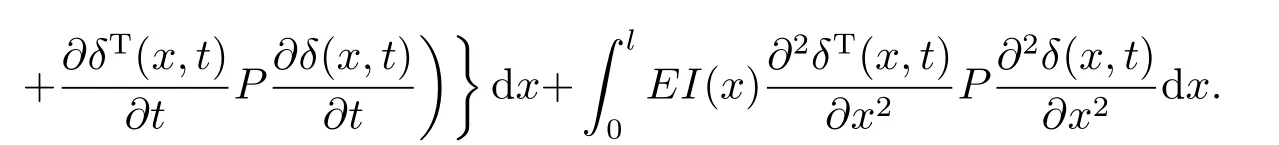
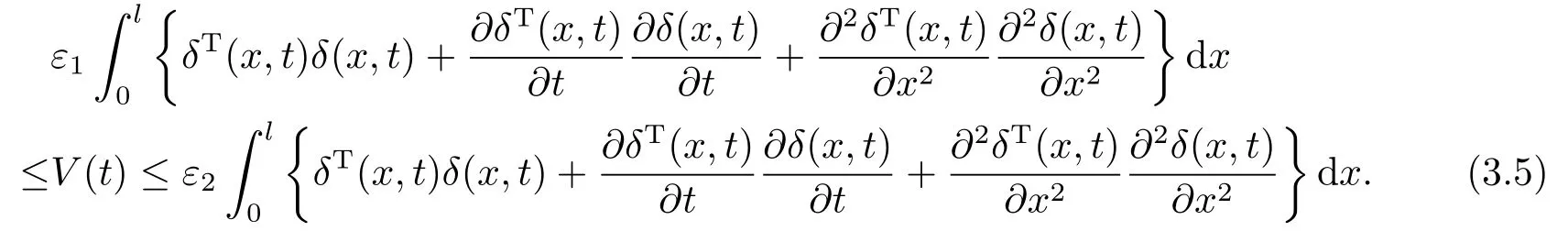
对V(t)求导,可得

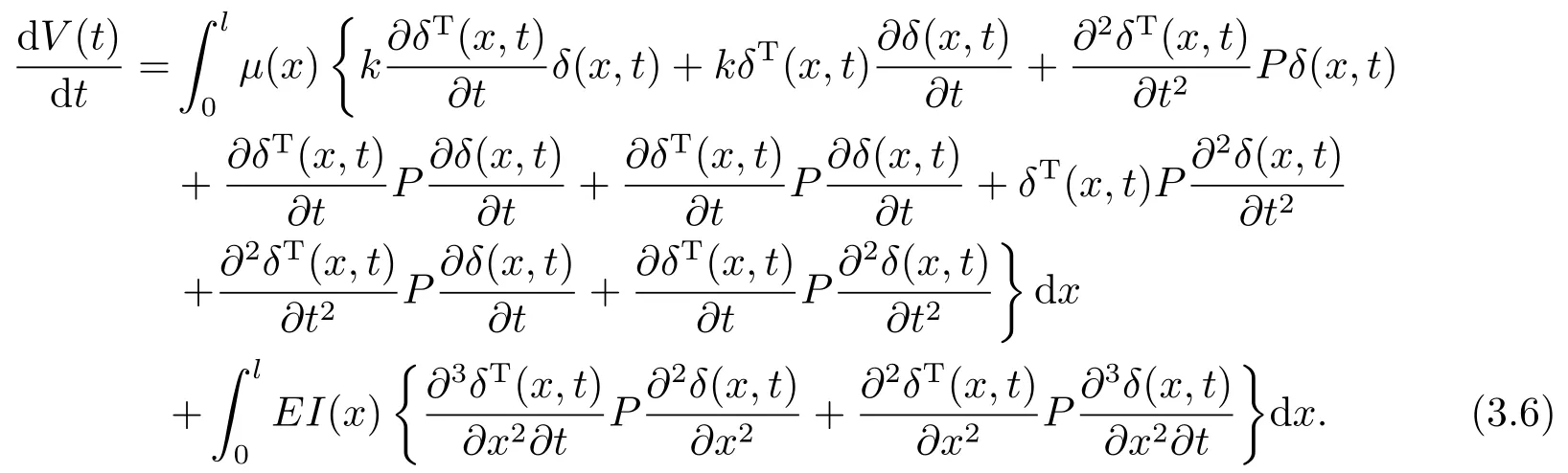
将(3.3)式代入(3.6)式中,有

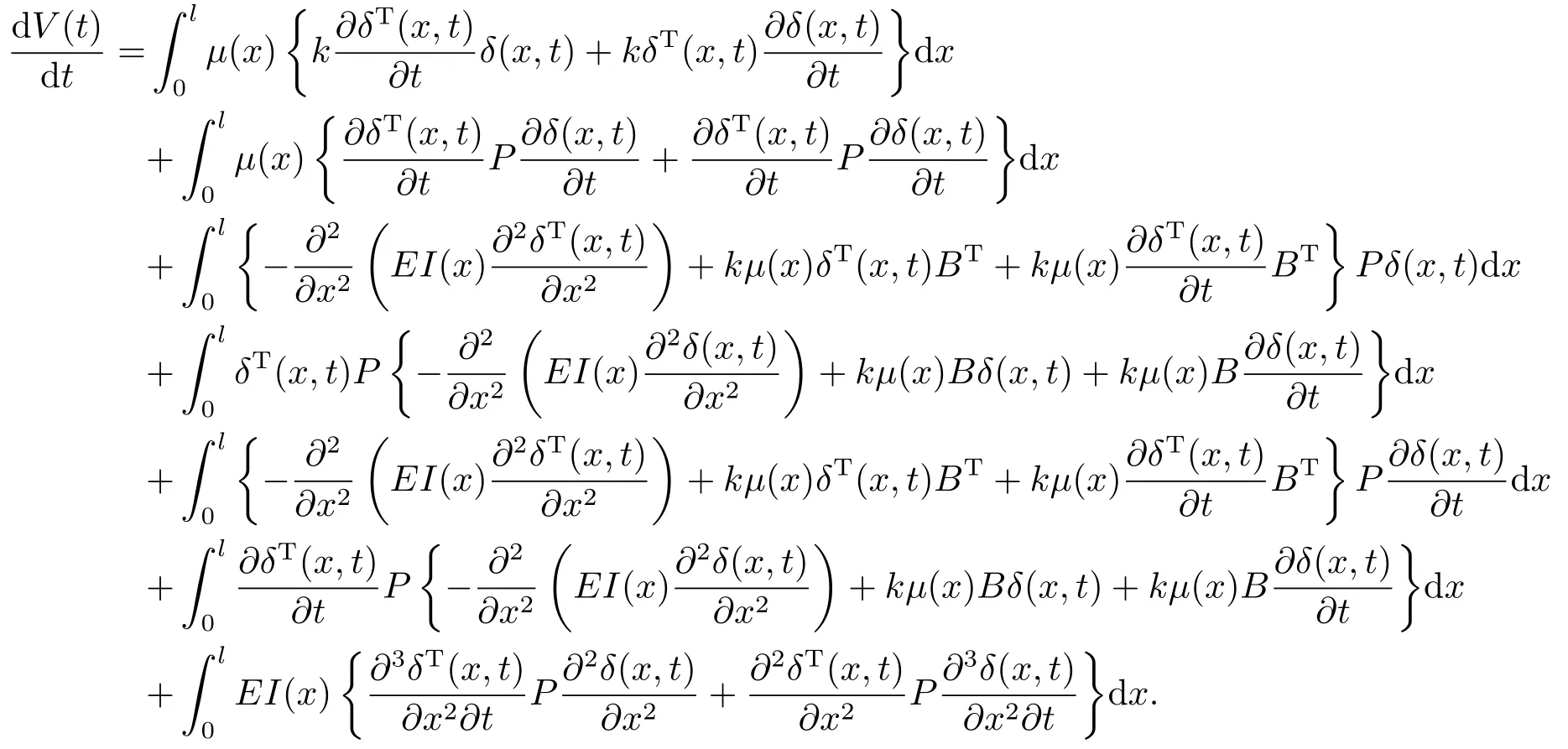
由(2.1)式,进一步有

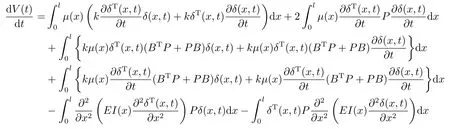
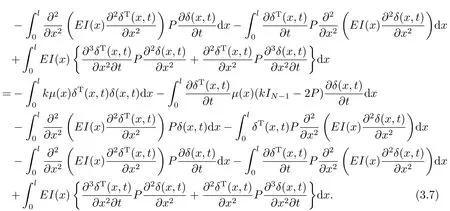
结合系统(2.4)的边值条件,利用分部积分可得

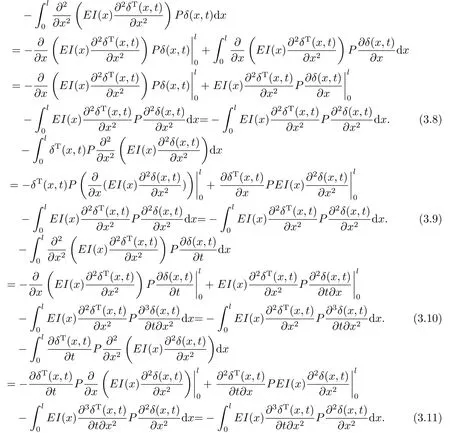
将(3.8)-(3.11)式代入到(3.7)式中,并结合(3.4),(2.3)式可得

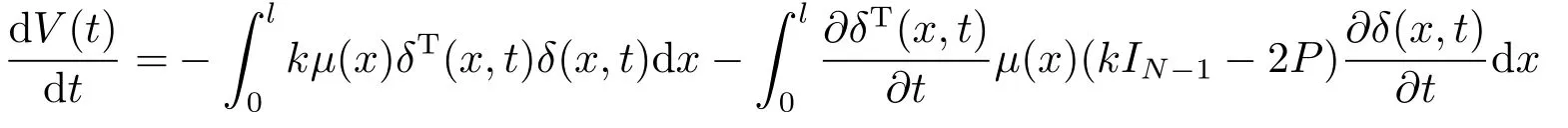
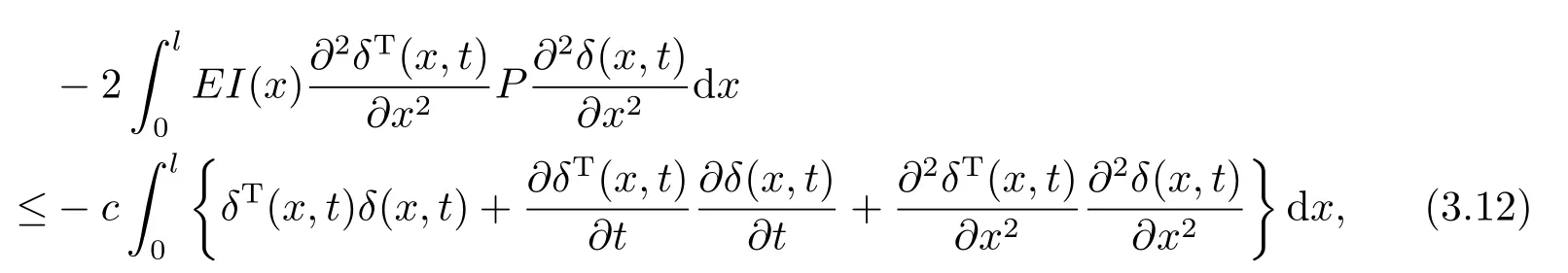
这里c=min{µ1(k −2λmax(P)),2EI1λmin(P)}.由(3.5),(3.12)式可得

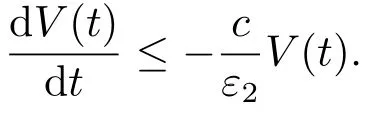
进一步有

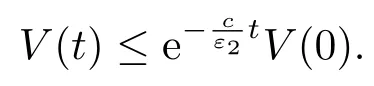
因此

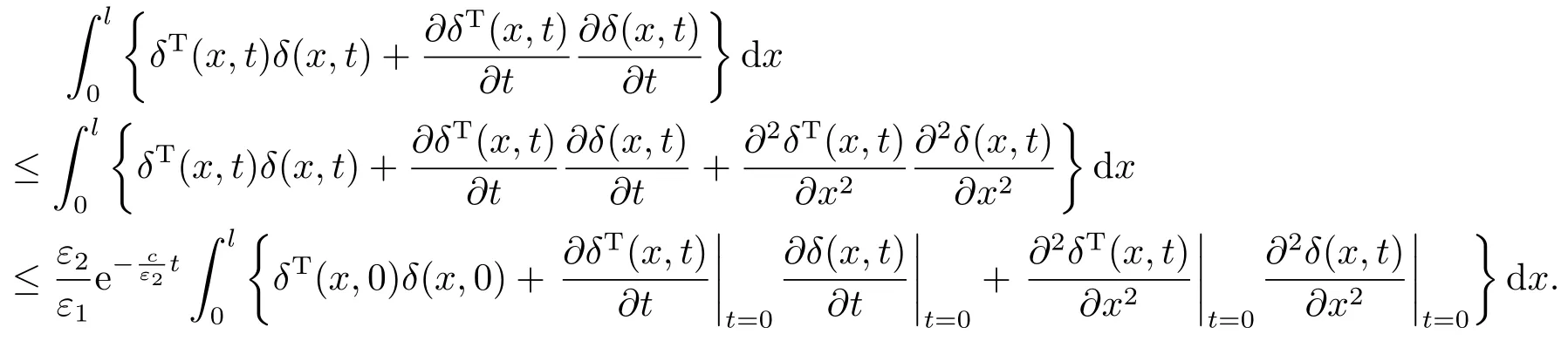
从而

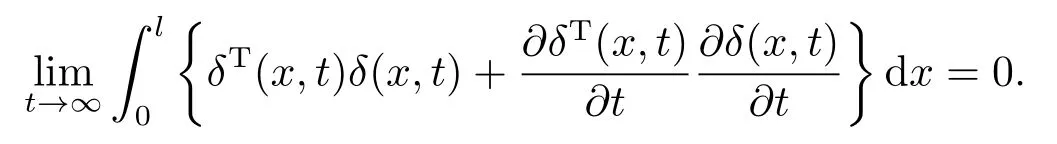
证毕.

4.仿真算例

考虑一个由三个智能体构成的多智能体系统,该多智能体的通信拓扑如图4.1所示,显然,假设2.1成立.系统的描述如下(µ(x)≡1,EI(x)≡1)：

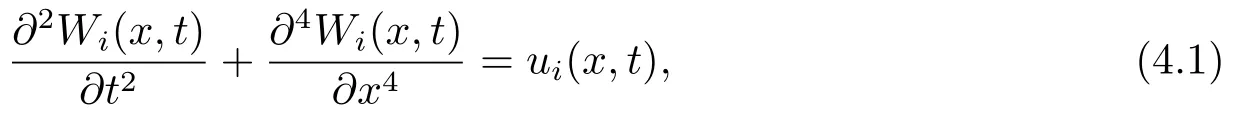
这里(x,t)∈(0,1)×(0,∞),i= 1,2,3.系统(4.1)的初、边值条件如下:Wi(x,0)=0.00001×

通信拓扑的加权邻接矩阵如下：

相应地有

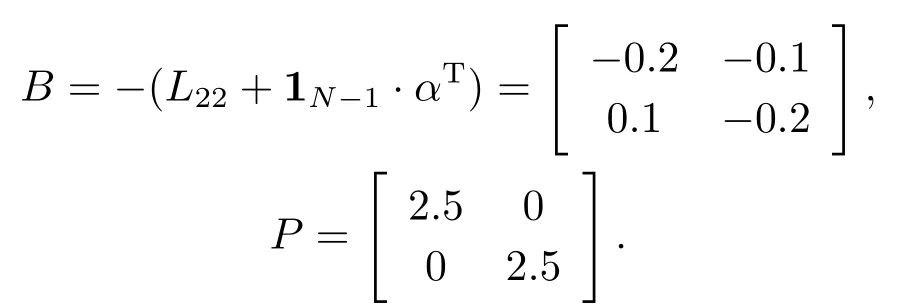
取k=7(>2λmax(P)),则在反馈控制律(3.1)的作用下,一致性误差的仿真结果见图4.2.

从图4.2可看出,状态变量的一致性误差∥δi∥L2(0,1)×L2(0,1)(i=2,3)随着时间的增长收敛到零.

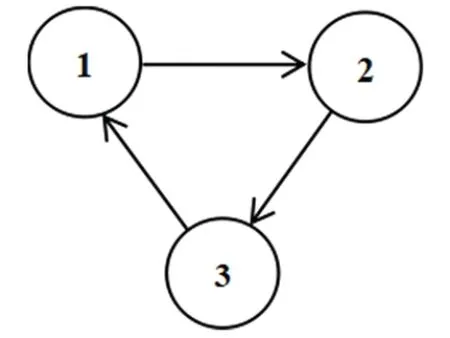
图4.1 网络拓扑G

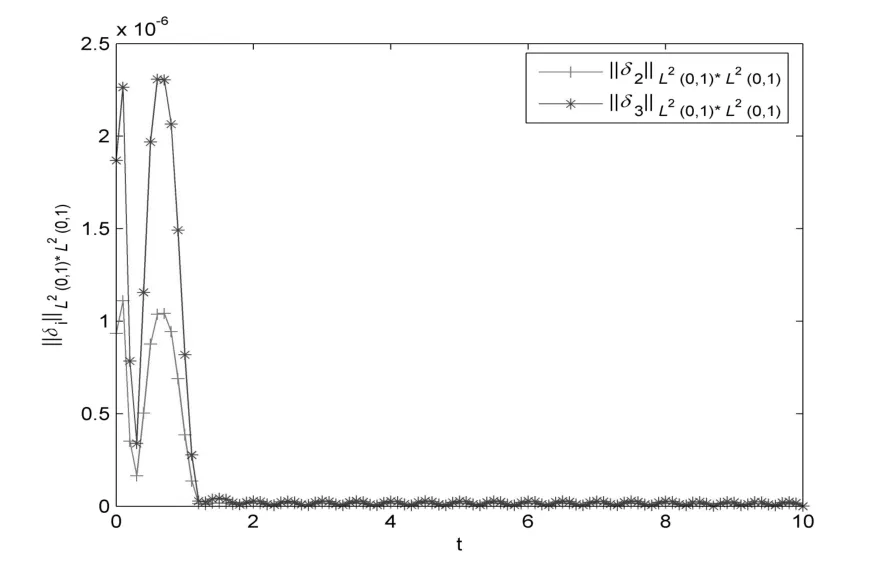
图4.2 ∥δi∥L2(0,1)×L2(0,1)的仿真结果

5.结论

本文研究了一类偏微分多智能体系统的一致性控制问题,该类系统中的每个智能体均由变系数四阶梁方程构建而成.通过构建合适空间上的Lyapunov泛函,得到一致性反馈控制律,当该反馈控制律作用于系统时,状态变量的一致性误差于L2(0,l)×L2(0,l)空间内收敛到零.有关偏微分多智能体系统的一致性控制问题,至今,相关的研究工作涉及的系统均为二阶的,还尚无针对高阶(四阶)系统的控制设计工作,而本文中的四阶系统又来源于实际问题中的梁方程(方程中的系数也具有相应的实际意义),由此,研究其一致性控制问题是有意义的.