Robust Optimal Reinsurance and Investment Strategies with Delay and Default Risk in a Jump-Diffusion Financial Market with Common Shock Dependence

JIN Bingyan(靳冰岩),MA Shixia(马世霞)

(School of Science,Hebei University of Technology,Tianjin 300401,China)

Abstract: In this paper,we consider a robust optimal reinsurance and investment problem with delay and default risk under jump-diffusion model.The insurer can trade in a risk-free asset,a defaultable bond and two risky assets whose price processes are described by jump-diffusion models and correlated through a common shock.Assume that the insurer is allowed to purchase proportional reinsurance,in particular,the reinsurance premium is assumed to be calculated via the mean-variance premium principle.Under the consideration of the performance-related capital inflow/outflow,the wealth process of the insurer is modeled by a stochastic differential delay equation.The insurer’s aim is to maximize the expected exponential utility of the combination of terminal wealth and average performance wealth to study the pre-default and post-default case respectively.Furthermore,closed-form expressions for the optimal strategies and the corresponding value function are derived.Finally,numerical examples and sensitivity analyses are provided to show the impact of various parameters on the optimal strategies.In addition,ignoring model uncertainty risk will lead to significant utility loss for the Ambiguity-Averse insurers.

Key words:Robust optimal contral;Jump-diffusion model;Common shock dependence;Stochastic differential delay equation;Default risk

1.Introduction

The insurer transfers the risk of large claims to other insurers by purchasing reinsurance,and at the same time invests the premium in different assets to achieve the maximum profit of the company.In recent years,the optimal reinsurance and investment problem in actuarial insurance has been widely investigated.[1−6]

In actuarial practice,most insurance companies base their premium on the expected value principle.The reason is,of course,mathematical convenience but this is also often due to a shortage of available statistical data.Against this principle,one can convincingly argue that two risks with the same mean may appear very different whereas the price list will give the same amount of premium for both of them.Relative to the expected value criterion,the variance premium criterion fully considers the volatility of losses.As an example,think of the family of the normal distributions with fixed meanµ0and parameterized by the varianceσ20.The premium will be constant (and equal to (1+θ)µ0)but everybody agrees that the underlying danger will strongly vary.SUN et al.[7]and ZHANG et al.[8]considered reinsurance control under the variance premium criterion.

In most studies of optimal investment or investment-reinsurance strategies,it is assumed that insurance companies have only one shock investment.In fact,many insurance companies have two or more lines of investment,and most of them are not independent of each other due to the risk of suffering from a common information shock.For example LIANG et al.[9]studied the optimal reinsurance-investment problems in a financial market with jump-diffusion risky asset,where the two jump number processes are correlated by a common shock.In addition,with the rapid development of financial markets,high-yield corporate bonds have become increasingly attractive to investors.Although there is indeed a default risk,it is often sought after due to its relatively high yield.In fact,the problem of portfolio optimization with defaultable securities has become an important research content in the field of insurance actuarial.[7,10−11].

Combined with practice,most of the literature on the robust optimal reinsurance and investment problem assumes that the ambiguity-averse insurers’ risky asset’s price process follows the diffusion model,which ignores the significant effect that jumps and default have on the optimal strategy.There are pronounced differences between ambiguity aversion with respect to(w.r.t.)diffusion,jumps,default risks.Therefore,in the portfolio selection problem,ignoring ambiguity w.r.t.the jumps and default risk may result in large losses in the financial market.[12−13]In addition,there is also a practical problem to consider that the development of real-world systems depends not only on their current state but also on their previous history.If we believe that financial market exists bounded memory or the performance-related capital inflow(outflow),then the wealth process with delay must be considered[11,14].

In this paper,under model uncertainty,we adopt a relatively classical diffusion approximation model for insurance surplus process;financial market is diffusive only,and consists of the defaulted bond,one risk-free asset and a pair of stocks where the price processes of the stocks is given by jump processes.We assume that there exists capital inflow into or outflow from the insurer’s current wealth,and the amount of the capital inflow/outflow is proportional to the past performance of the insurer’s wealth.In that case,the wealth process of the insurer is governed by a stochastic delay differential equation (SDDE).Our goal is to maximize the expected exponential utility of the terminal wealth to find an optimal strategy and corresponding optimal value function,in as explicit a closed form as possible.

The remainder of the paper is organized as follows.Section 2,we describe the model and necessary assumptions.In Section 3,we state the robust optimal investment-reinsurance problem with exponential utility under default risk.In Section 4,we study a post-default case and a pre-default case,respectively,and derive explicit solution for the two problems.In Section 5,we present the numerical results and graphs for illustrative our results.

2.Model Assumption

Suppose (Ω,F,P)be a given complete probability space with a filtrationF={F}t≥0is the information of the market available up to timet.[0,T] is a fixed time horizon.All the processes introduced below are assumed to be adapted to{Ft,t ∈[0,T]}.In the classical risk model,without investment and reinsurance,the insurer’s surplus process is modeled by

wherec >0 is the premium rate,{Yi}is theith claim andK(t)is a Poisson process with intensityλk>0.{Yi}is assumed to be independent and identically distributed positive random variables with finite mean E[Y i] =µyand second moment E[(Yi)2] =σy.Furthermore,we assume that claims{Yi}are independent ofK(t)and the premium ratecis calculated by the expected value premium,i.e.,c= (1+θ)λkµy,whereθ >0 is the insurer’s safety loading.To be protected from potential large claims,the insurer is allowed to purchase proportional reinsurance to disperse risk.Letα(t)∈[0,1] be the reinsurance retention levels at timet.And the aggregate reinsurance premium under the mean-variance principle takes the form

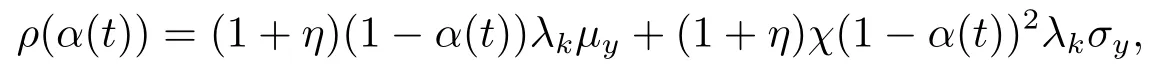
whereη,χ >0.From [8],joining the reinsurance and the surplus process for insurance is approximated as

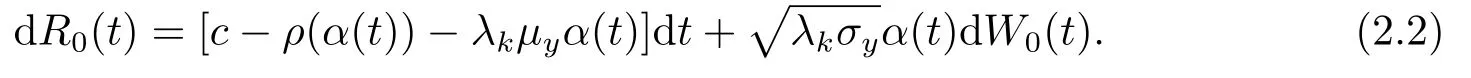
Remark 2.1Whenη >0,χ= 0,the reinsurance premium rate degenerates to the expectation premium rate.

Remark 2.2Whenη=0,χ>0,the reinsurance premium rate is calculated under the variance premium principle.

In addition to reinsurance,the insurer also can invest in a risk-free asset,a pair of shocks and a defaultable bond.The price process of the risk-free asset is described by

wherer0>0 is the constant risk-free interest rate.The price processes of the other two risky assets are respectively modeled by the following jump-deiffusion processes

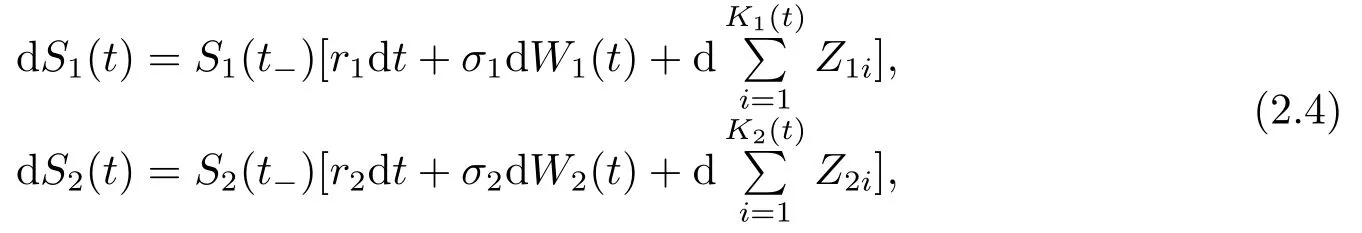
wherer1,r2are the appreciation rates,σ1,σ2>0 are the volatility coefficients.W1(t)andW2(t)are independent standard Brownian motions.In addition,{K1(t)}t≥0,{K2(t)}t≥0are two counting processes.It is assumed thatZ1iandZ2iare independent jump amplitude of the risky assets’ priceS1(t)andS2(t),respectively,they are independent ofK1(t)andK1(t)and their moments are denoted by E[Z1i]=µ1z,E[(Z1i)2]=σ1z,E[Z2i]=µ2z,E[(Z2i)2]=σ2z.

The two counting processes are correlated in the way that

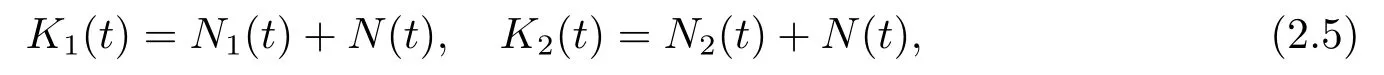
withN1(t),N2(t),N(t)being three independent Poisson processes with parametersλ1,λ2,andλ,respectively.It is obvious that the dependence of the two classes of risky asset is due to a common shock governed by the counting processN(t).

Remark 2.3HereN(t)represents the common information in the financial market,and the common information has a common influence on the financial market.More vividly,in the same financial market,the common information may be caused by news that affects the entire market such as interest rates,credit spreads or oil prices.

In the development of this study,we use Poisson random measureKj(·,·)(j= 1,2)onΩ×[0,T]×[−1,+∞] to denoteandas

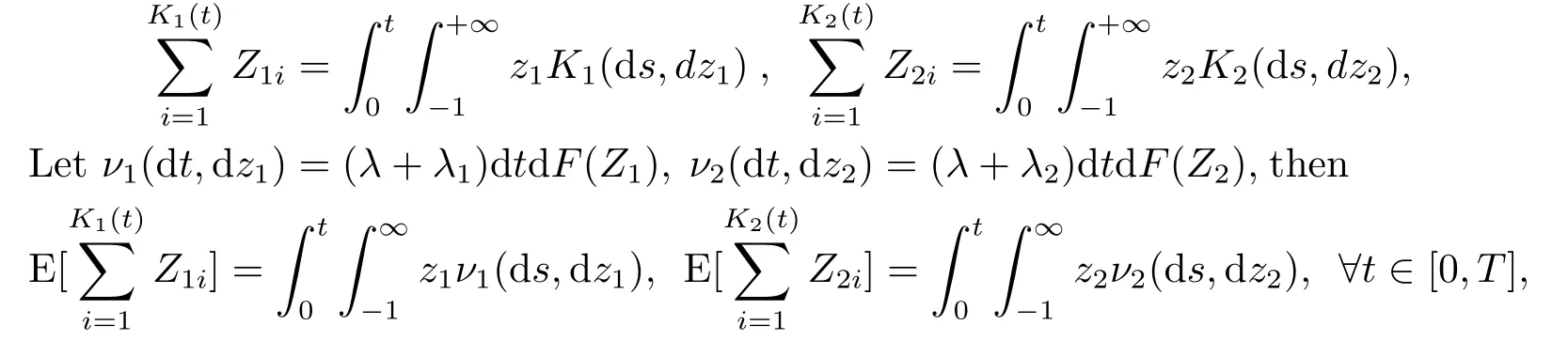
andνj(·,·)is the compensator of the random measureKj(·,·).Therefore,the compensated measure(·,·)=Kj(·,·)−νj(·,·)is related toas follows

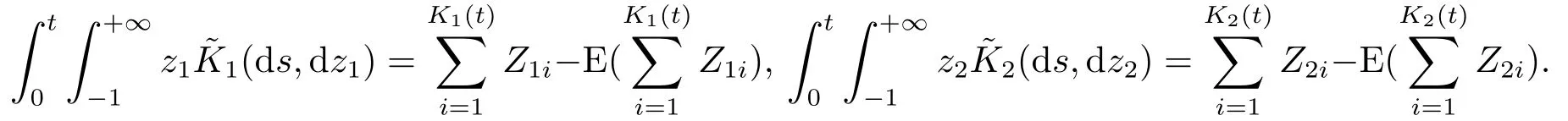
Next,we introduce the defaultable bond.Denoteτby the first jump time of a Poisson process with constant intensityhP >0,which represents the default time of the company issuing the bond.Fort≥0,define a default process byH(t)= 1{τ≤t},which is a nondecreasing right continuous process and makes a discrete jump at the random timeτ,where 1 is an indicator function which has value one if there is a jump and zero otherwise.We useHt=σ(H(ν),0≤ν ≤t)andGt=Ft ∨Ht,t ≥0,thenG=(Gt)t≥0,is the smallest filtration such thatτis a stopping time.Furthermore,the associated martingale default process can be written as

Similarly,we assume that there exists a defaultable bond with a maturity dateT1and that the default time isτ.Let 1/∆≥1 denote the default risk premium andς ∈[0,1]be the loss rate of the bond when a default occurs.By Girsanov’s theorem,we find that there exists a risk neutral measureQ(which is equivalent toP)and underQ,the arrival intensity of default is given byhQ=hP/∆.Denotep(t,T1)to be the price process of the defaultable bond,then based on the definitions ofH(t)andMP(t),the dynamics of the defaultable bond price underPis given by

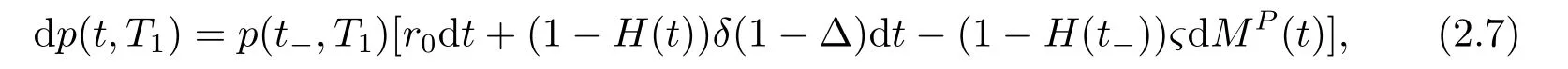
whereδ=hQςis the risk neutral credit spread.

In what follows,we formulate a wealth process with delay,which is caused by the instantaneous capital inflow into or outflow from the insurer’s current wealth.We describe the instantaneous amount of the capital inflow/outflow as proportional to the past performance of the insurer’s current wealth by using a linear delay equationfdefined as

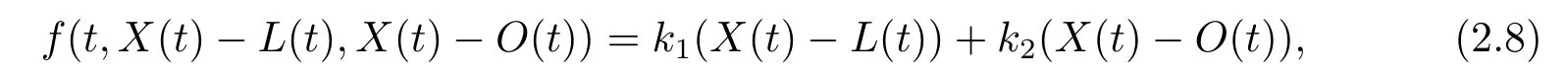
wherek1andk2are nonnegative constants,andrepresent given functionals of the path segmentXt={X(t+s),s ∈[−ν,0]}.Hereρis the given nonnegative average parameter,νstands for the time of delay and is the duration of the past that the investor usually cares about.In the delay function (2.8),X(t)−L(t)represents the average performance of the wealth betweent −νandt,whileX(t)−O(t)accounts for the absolute gain/loss of the insurer’s wealth in the period[t −ν,t].

Denoteβ1(t),β2(t)andβ3(t)the money amount invested in the stocks and the defaultable bond,respectively,andα(t)represents the risk exposure of the insurer.The trading strategy is represented byu={α(t),β1(t),β2(t),β3(t)}.Thus,the wealth processXu(t)can be presented by the following SDDE

3.Robust Optimal Control Under Exponential Utility

Following the existing literature on stochastic control with delay,[4,11],we suppose that the insurer is concerned with not only the terminal wealthXu(T)but also the average wealth over the period [T −ν,T],i.e.,L(T),meanwhile,in the paper we suppose that the aim of the insurer is to maximize the expected exponential utility of the combination of terminal wealth and average performance wealth.So the ambiguity-neutral insurer(ANI)maximizes the expected terminal wealth as

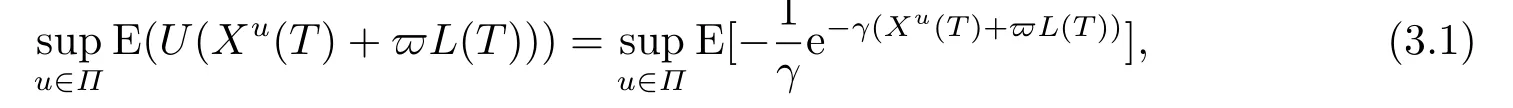
whereγis the pre-specified risk aversion coefficient,Πis the set of all admissible strategiesuin a given market and is given in the following definition 3.1,E[·] = E[·|Xu(t)=x,L(t)=l,H(t)=z].

Recent studies have shown that investors in the market are most often ambiguity-averse in reality.They propose the optimal strategies under worst case scenario.In this paper,we will incorporate ambiguity into the optimal problem for an ambiguity-averse insurer(AAI).We assume the alternative models are characterized by a class of probability measures which are absolutely continuous with respect to probability measureP.

To introduce the ambiguity on the diffusion,jumps,default risks,we define a set of prior probability measures as follows.First of all,we call the probability distortion function

ϕ(t):=(ϕ1(t),ϕ2(t),ϕ3(t),ϕ4(t),ϕ5(t),ϕ6(t))and satisfy

1)ϕ(t)areG-progressively measurable,for eacht ∈[0,T];

We denoteΣfor the space of all such functionsϕ.Each probability distortion functionϕ ∈Σassociates to a probability measureP∗∼Psuch that the Radon-Nikodym derivative processis

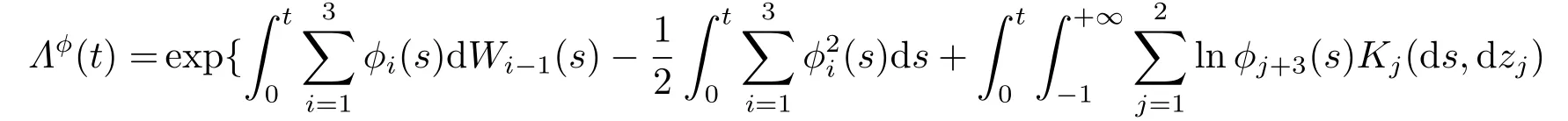
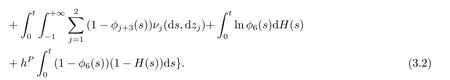
According to Girsanov’s Theorem,under the new alternative measureP∗,the stochastic processesWi(t)P∗are standard Brownian motions,where

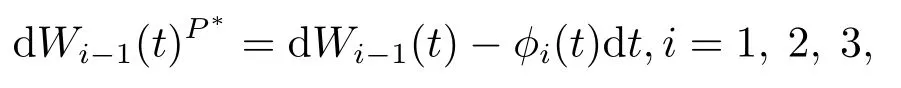
and the intensities of the corresponding Poisson process are become (λ+λ1)ϕ4,(λ+λ2)ϕ5,hPϕ6.

Thus,the dynamics of the wealth process underP∗is

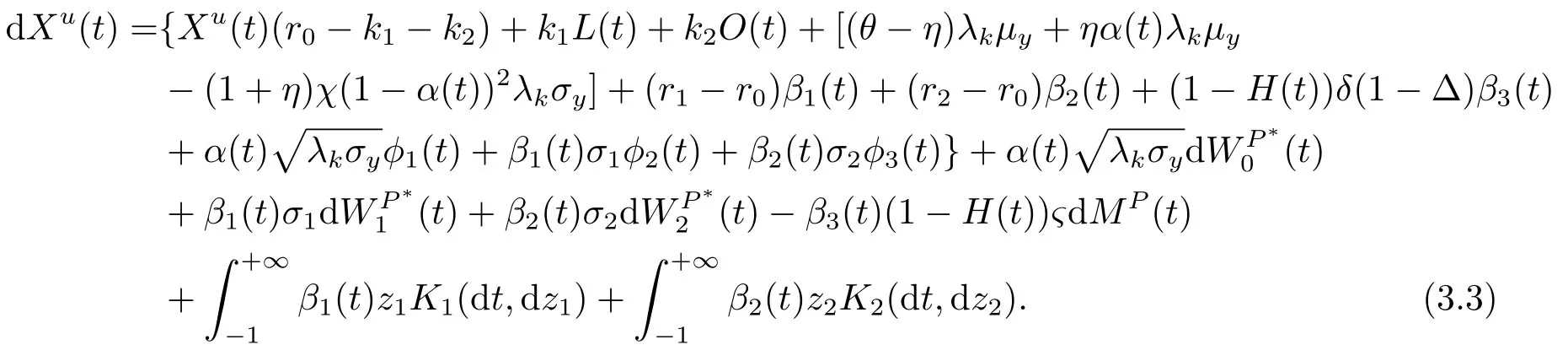
Definition 3.1(Admissible strategy)For any fixedt ∈[0,T],a strategyu={α(t),β1(t),β2(t),β3(t)}is said to be admissible if it satisfies

(i)uisG-progressively measurable with

(ii)∀x ∈R,the corresponding stochastic differential equation(3.3)has a pathwise unique solutionXu(t)withXu(t)=x,L(t)=landH(t)=h.

Here∥u(t)∥2=α2(t)+β21(t)+β22(t)+β23(t),and denote byΠthe set of all admissible strategies.

Inspired by[11],we can modify the problem(3.1)and define the value function as follows

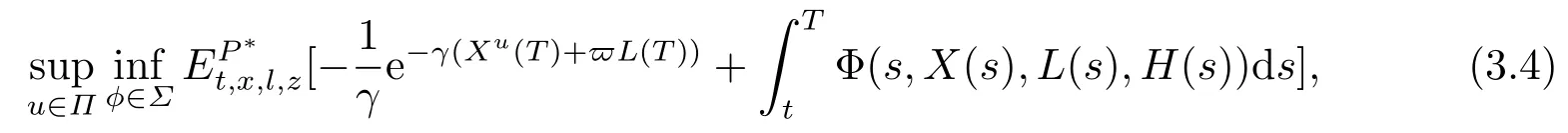
where

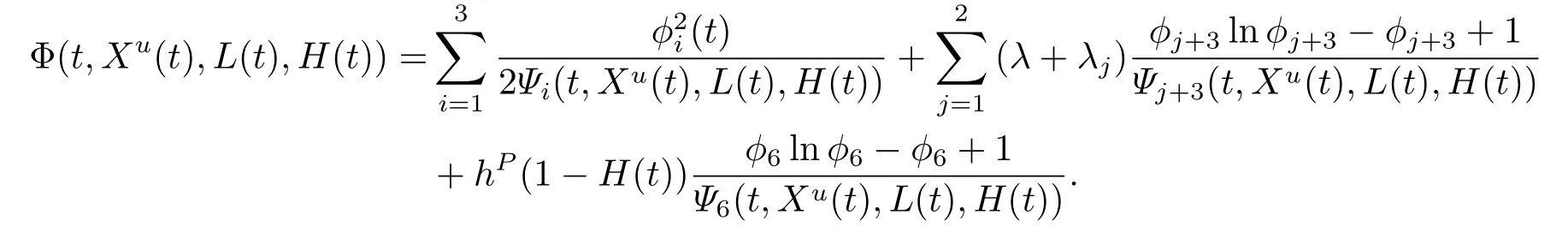
4.Optimal Robust Reinsurance and Investment Strategies

The purpose of this section is to find the portfolio optimization and the optimal proportional reinsurance strategyα(t)under the worst-case scenario.According to the dynamic programming principle,the extended HJB equation can be derived as follows:

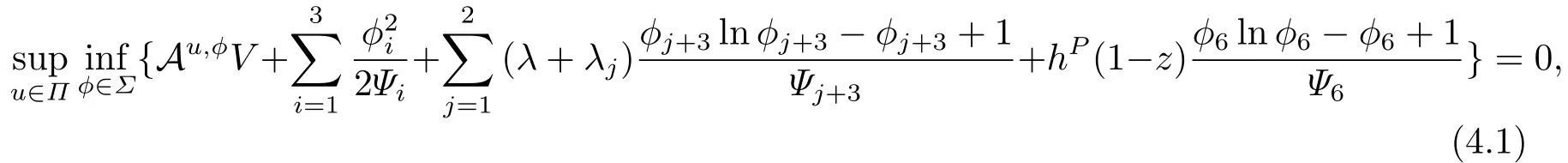
with the boundary conditionV(T,x,l,z)=−γ1e−γ(x+ϖl),whereAu,ϕVis the variational operator and is defined by

Au,ϕV(t,x,l,z)

For convenience,we choose a statedependent expression for the preference parameters,and leti=1,2,3,4,5,6.

In the following,we will derive the explicit solutions to the HJB equation (4.1)with preference parameter for the post-default case and the pre-default case,respectively.

As we can see in the equation (3.3),the change of the wealth processXu(t)depends on the delay variablesL(t)andO(t).For the sake of tractability,we impose additional conditions on the controlled delay system,

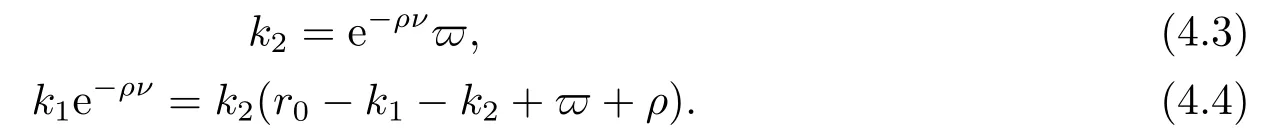
We will concentrate on the post-default case.Letz= 1 in (4.1).By the expression ofAu,ϕin (4.2),we rewrite (4.1)as

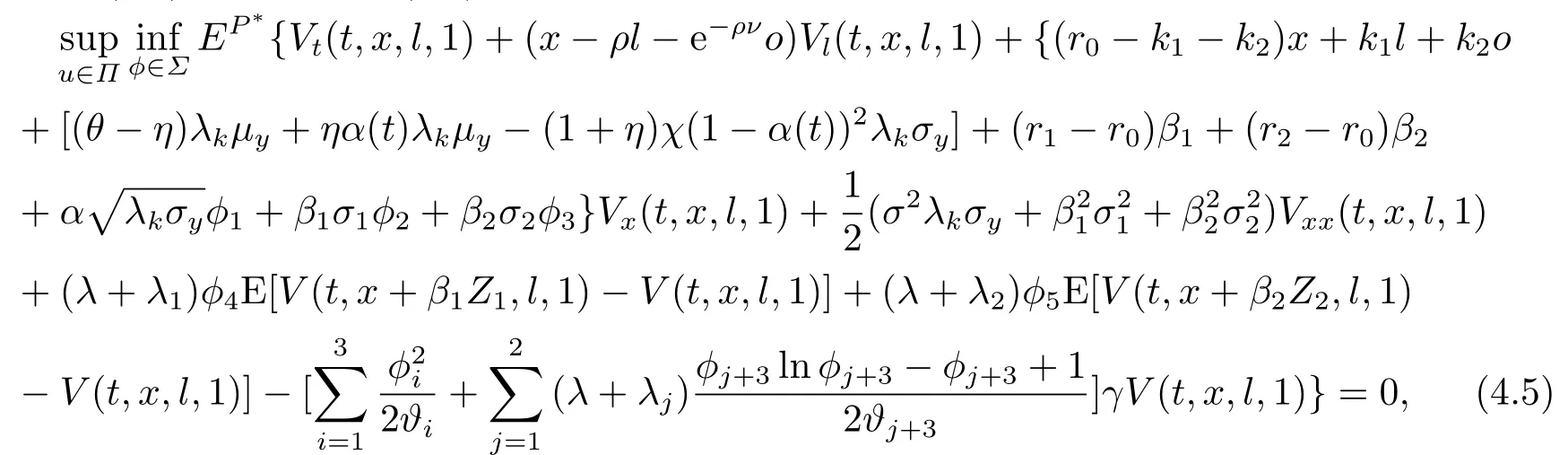
whereg(t)is a deterministic function withg(T)=0.A direct calculation yields

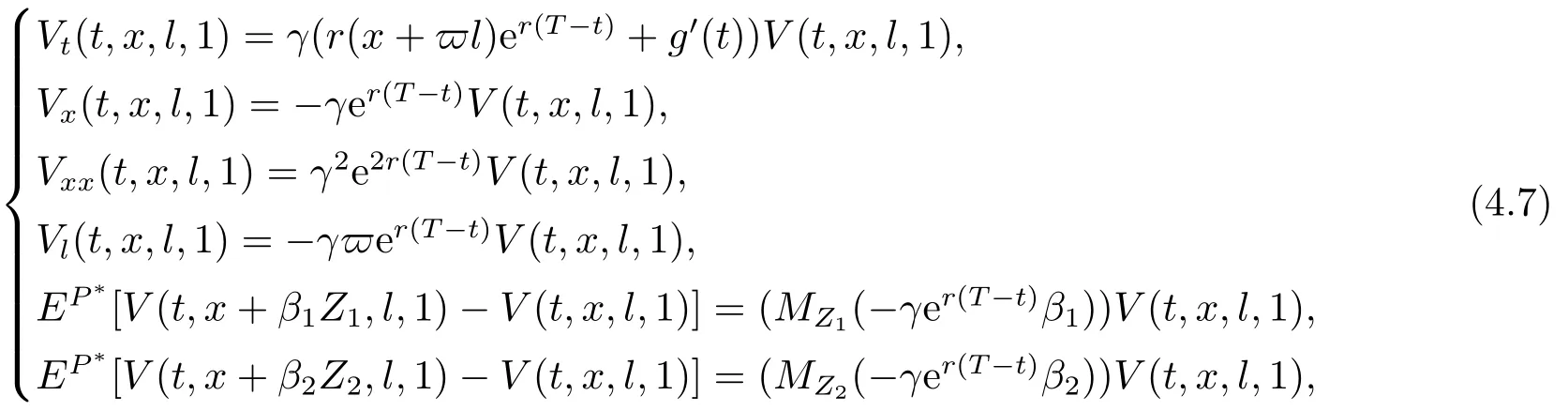
whereMZ1(ε):=EP∗[eεZ1]=EP[eεZ1];MZ2(ε):=EP∗[eεZ2]=EP[eεZ2].Note that the second and the fourth equality are due to the assumption that the distribution of the claim{Z1},{Z2}are restricted to be identical underPandP∗.

Substituting (4.7)into (4.5),we obtain

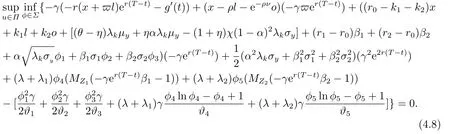
Differentiating (4.8)w.r.t.ϕ1(t),ϕ2(t),ϕ3(t),ϕ4(t),ϕ5(t)gives

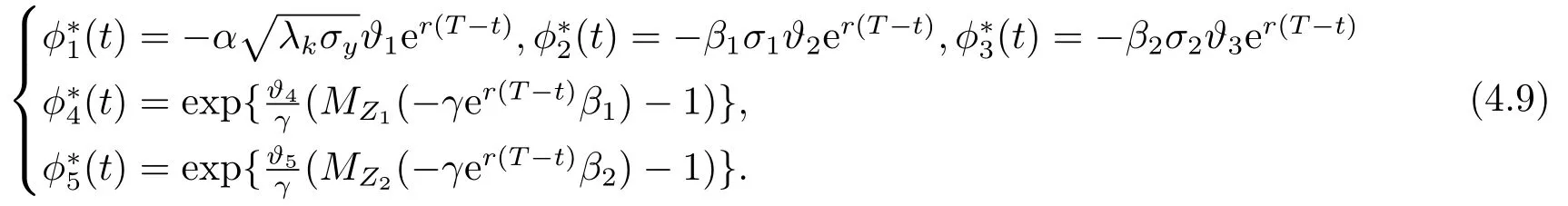
Substituting (4.9)into (4.8),we can obtain

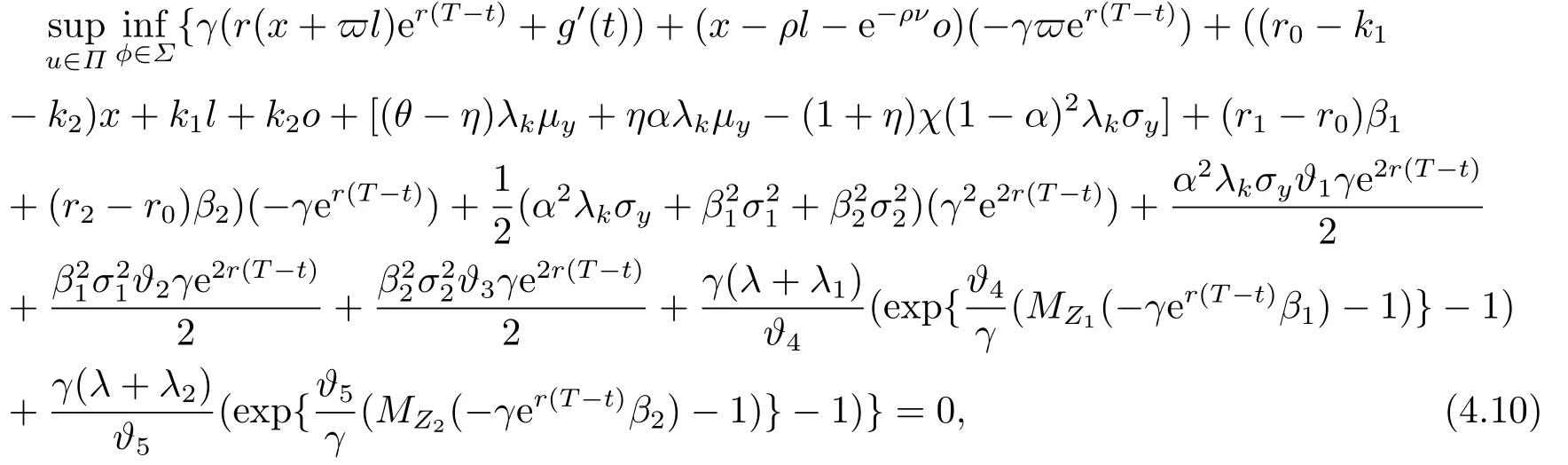
and differentiating (4.10)w.r.t.α(t),β1(t),β2(t)gives

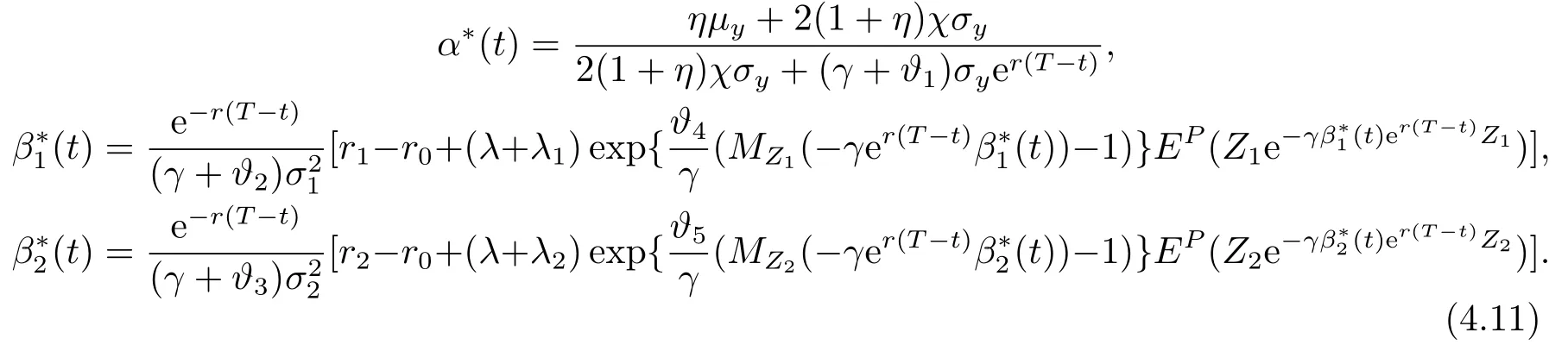
Theorem 4.1Equations(4.9),(4.11)indeed admit a unique solutionϕ∗(t)=(ϕ∗1(t),ϕ∗2(t),ϕ∗3(t),ϕ∗4(t),ϕ∗5(t)),u∗= (α∗(t),β∗1(t),β∗2(t)).More specifically,β∗1(t),β∗2(t)is the unique root of the function respectively defined by

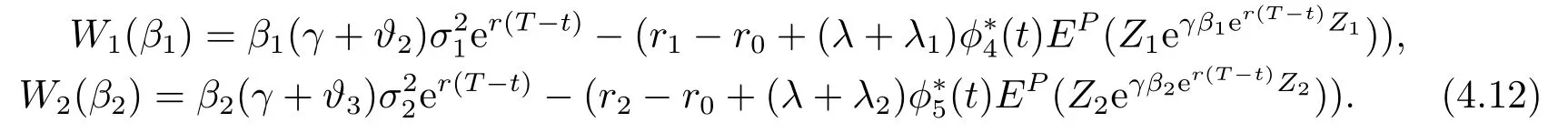
ProofIt is easy to verify thatW1(β1),W2(β2)defined by (4.12)is an increasing function of the variableβ1,β2,respectively.Moreover,W1(0)=−(r1−r0+(λ+λ1)µ1z)<0,>0 by the fact thatMZ1(−γer(T −t))>1 and eγer(T −t)Z1>1.

Thus,the functionW1(β1)=0 admits a unique root.The same reason to analyzeW2(β2)has a unique solution.

Replacing (4.11)back into (4.10),and using (4.3)-(4.4),we obtain that satisfies the following ordinary differential equation (ODE):

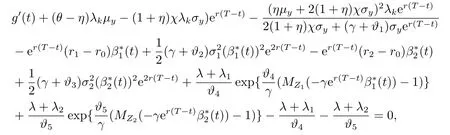
thus

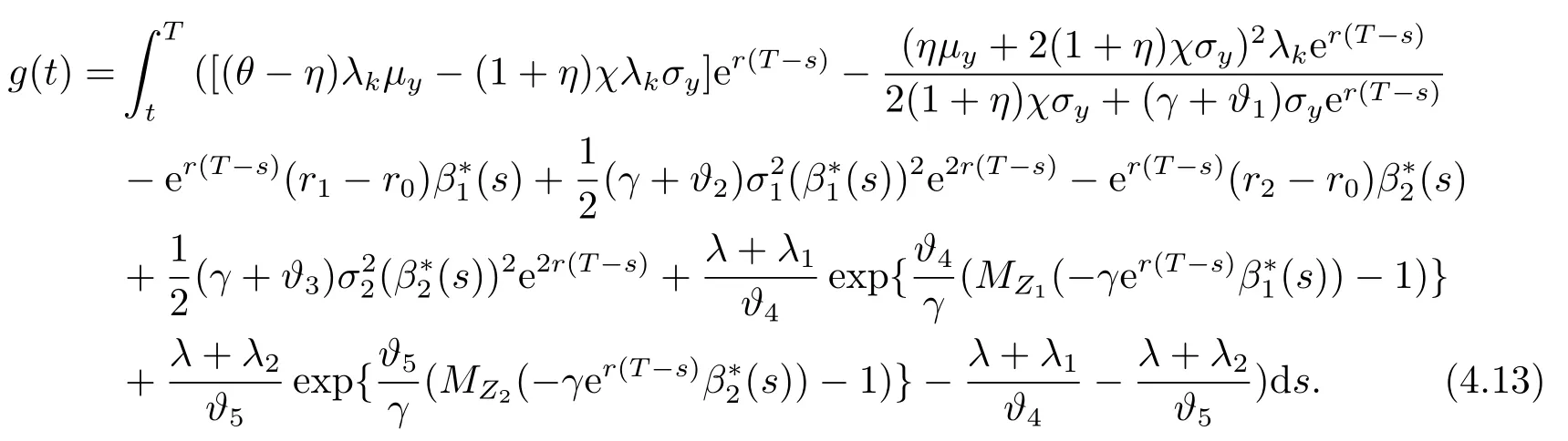
Remark 4.1The robust optimal portfolio optimization strategyβ∗1(t),β∗2(t)depend on the absolute risk aversion coefficientγ,the ambiguity aversion coefficientϑ2,ϑ3respectively and the parameters of insurance market.Moreover,whenη >0,χ= 0,the reinsurance strategy is similar to that in [15],which considered the robust optimal portfolio selection under the mean-variance criterion;whenη= 0,χ >0,the reinsurance strategy is similar to that in [7].

Next we will deal with the pre-default case.Letz= 0 in (4.1),the HJB equation (4.1)turns into

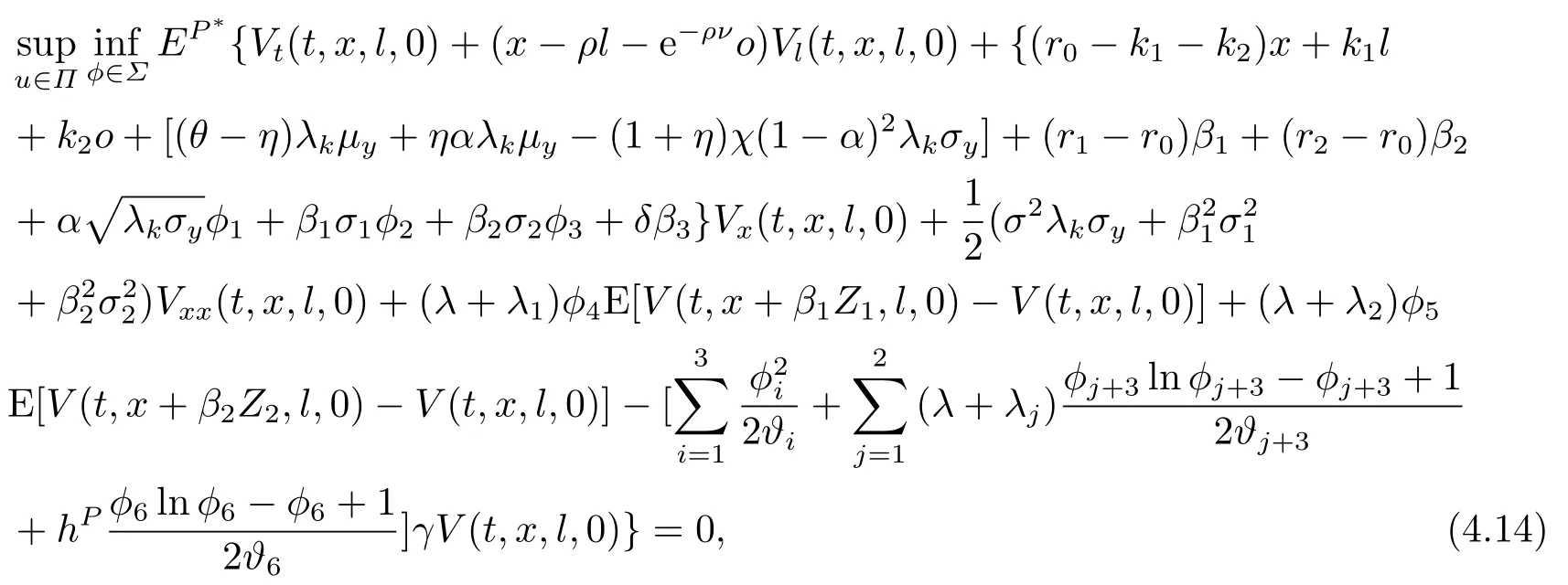
with the boundary conditionV(T,x,l,0)=−.We try the following form of the value function

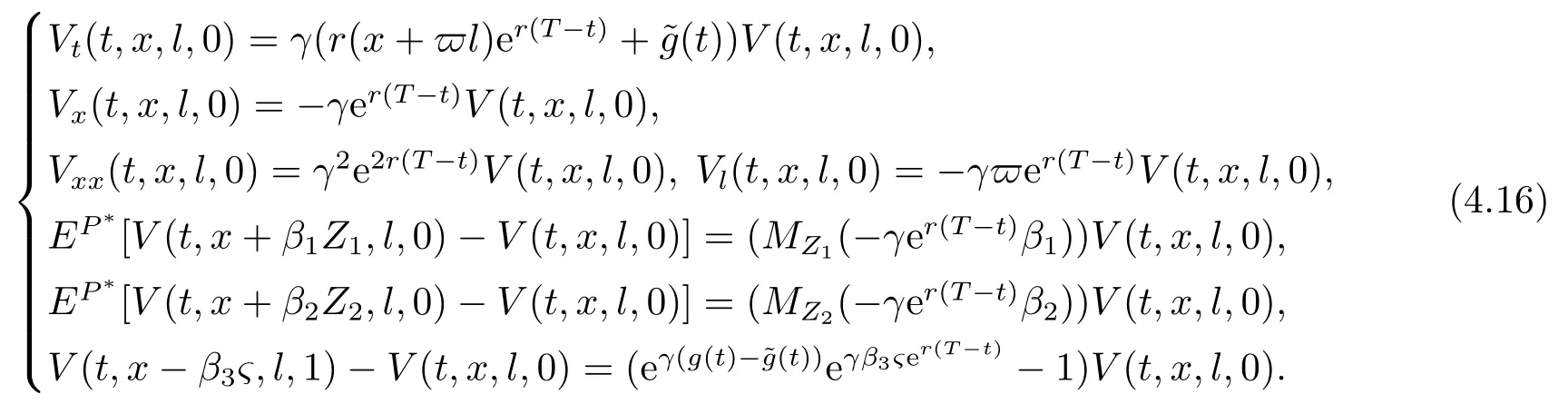
Substituting (4.16)back into the equation (4.14)yields

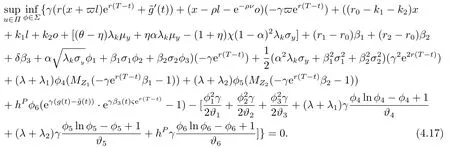
As in the post-default case,maximizing overϕyield the following first-order condition for the maximum pointϕ∗(t)=(ϕ∗1(t),ϕ∗2(t),ϕ∗3(t),ϕ∗4(t),ϕ∗5(t),ϕ∗6(t)):

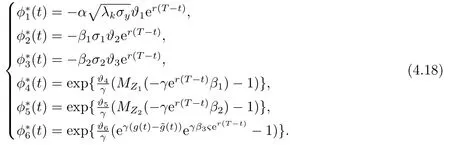
Plugging (4.18)into (4.17)and minimizing overuyields the following first-order optimality conditions for the robust optimal strategy

Theorem 4.2LetthenW(ϕ6)has a unique positive rootϕ6.

ProofSinceit is easy to verifyW(ϕ6)is a decreasing function onand increases onMoreover,Therefore the functionW(ϕ6)= 0 admits a unique positive rootϕ∗6>0.

Substituting(4.18),(4.19)and into(4.17),we obtain that satisfies the following ordinary differential equation (ODE):

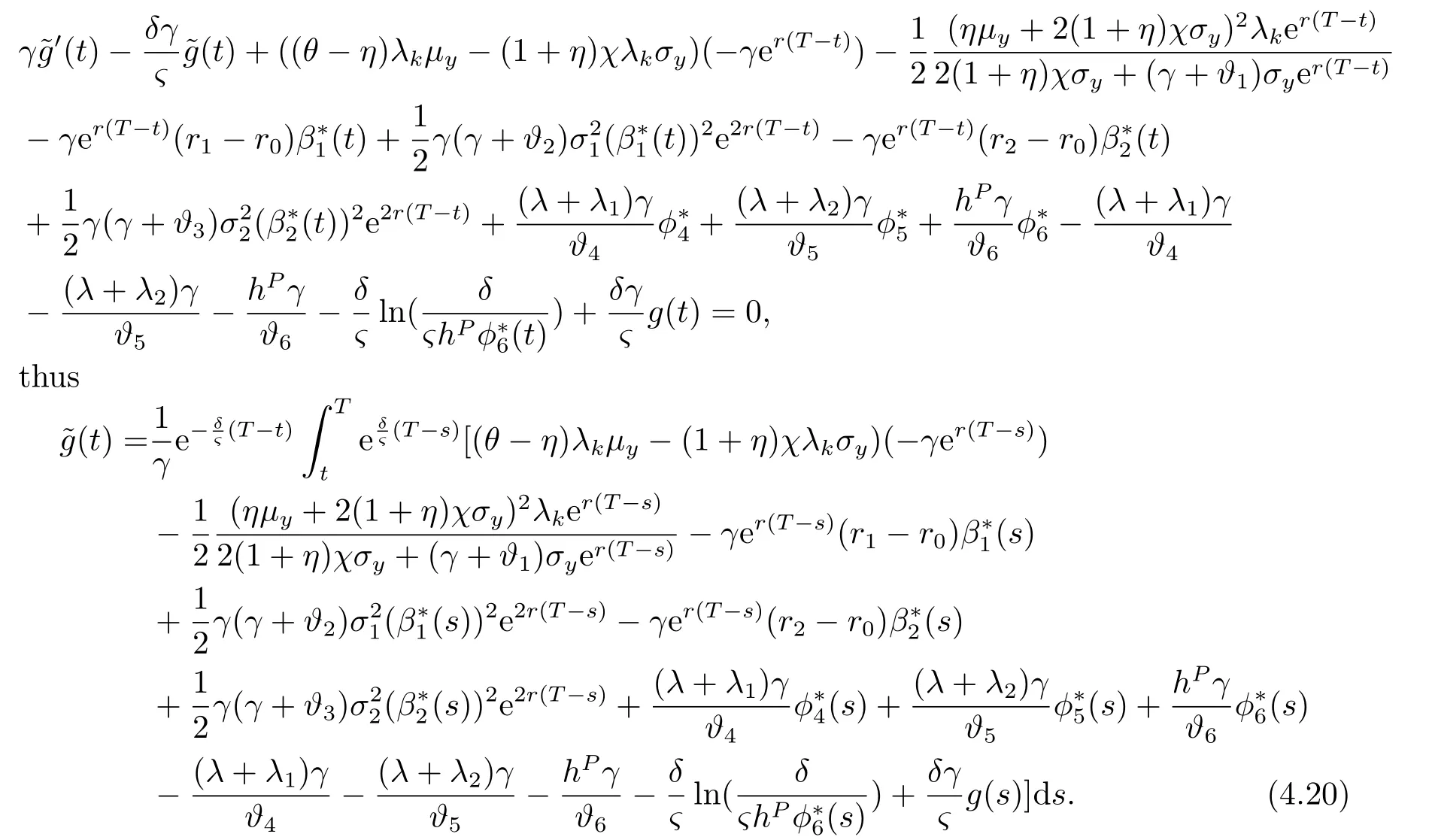
Finally,putting the pre-default and post-default case together,we have the following solution to the HJB equation (4.1)associated with the value functionM(t,x,l,z)

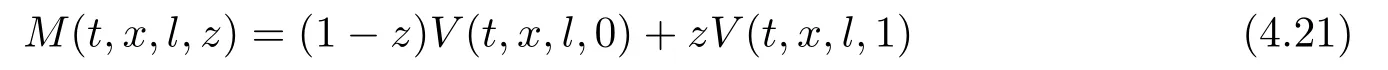
wherez=1 orz=0,andV(t,x,l,1),V(t,x,l,0)defined in(4.6),(4.15),respectively.

The robust optimal strategy is given by

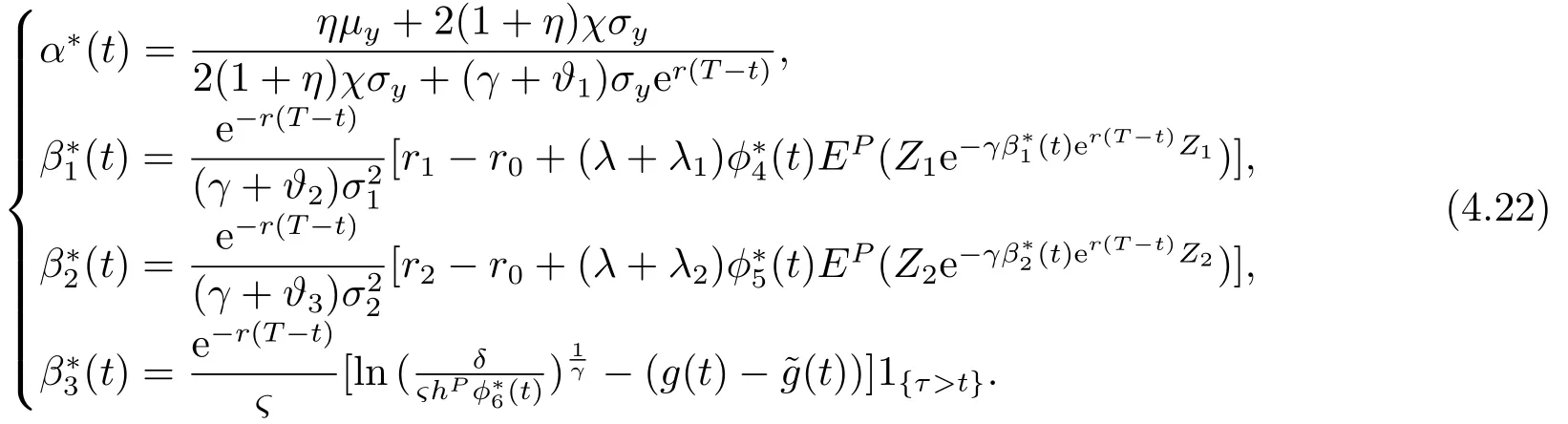
The worst-case measureϕ∗(t)= (ϕ∗1(t),ϕ∗2(t),ϕ∗3(t),ϕ∗4(t),ϕ∗5(t),ϕ∗6(t))is given by equation (4.18).g(t)and(t)are given by (4.13)and (4.20).Note thatβ∗1(t),β∗2(t)andβ∗3(t)are unique solutions to the respective equations.

Theorem 4.3If there exists a function and a control policy (α∗(t),β∗1(t),β∗2(t),β∗3(t)),which satisfy the HJB equation (4.1),thenM(t,x,l,z)is the corresponding value function and(α∗(t),β∗1(t),β∗2(t),β∗3(t))is an optimal strategy.

ProofFrom [11],the above theorem will hold if (α∗(t),β∗1(t),β∗2(t),β∗2(t))and the corresponding candidate value functionM(t,x,l,z)has the following three properties:

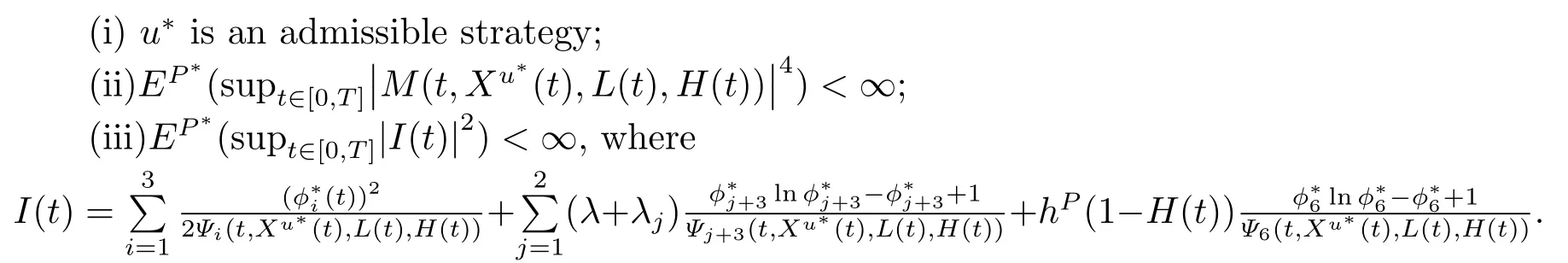
The proof of the above three properties can be found in [11],so we omit it here.

5.Suboptimal Strategy

To evaluate the importance of taking ambiguity into account,we determine how much an insurer suffers from ignoring it.Next we investigate the utility loss of the insurer when ignoring the effects of ambiguity.The strategy of the ANI is called the suboptimal strategy.When the AAI adopts the suboptimal strategy,the corresponding value function is defined by

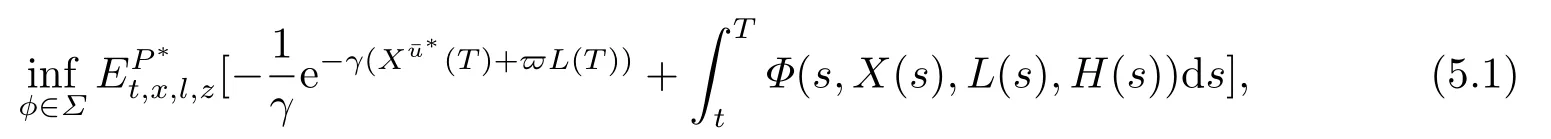
We can solve the problem (5.1)by using the similar HJB equation as that in Section 4.2.We find that the worst-case measure for the problem (5.1)has the similar expression as Eq.(4.18),only need to changeg(t)to the functiong1(t),and(t)to the function(t).Via a calculation that is parallel to the method in Section 4,we obtain the value function for optimization problem (5.1)under the suboptimal strategy as follows:

where

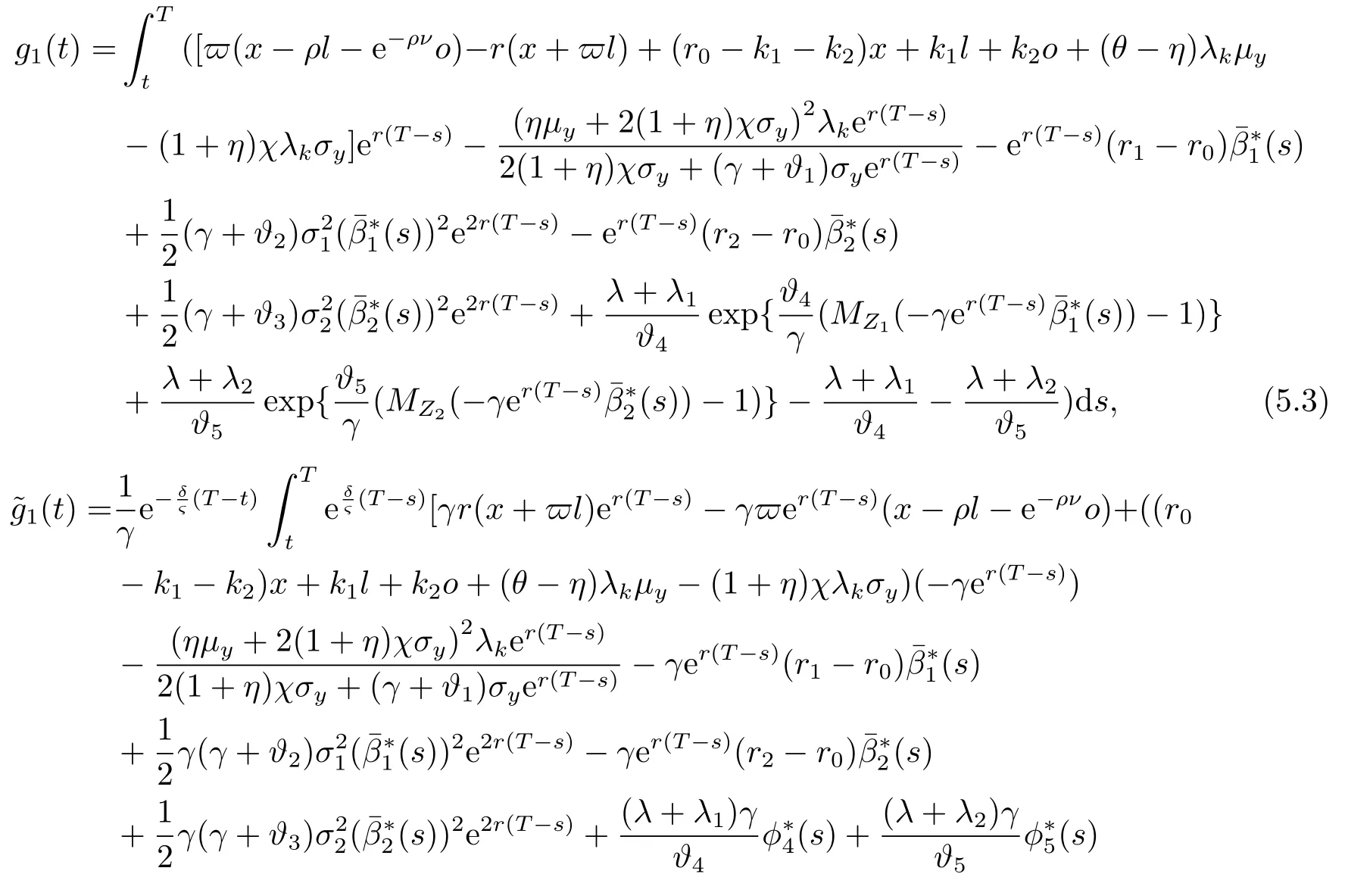
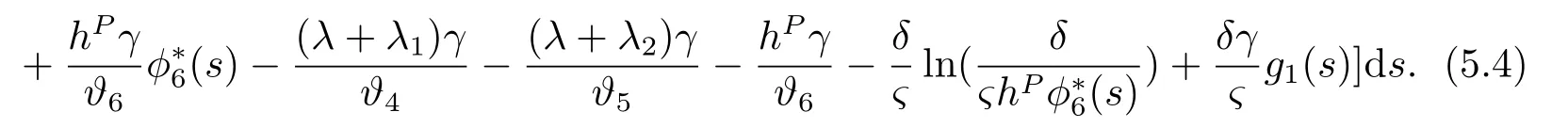
Then we define the post-default utility loss as

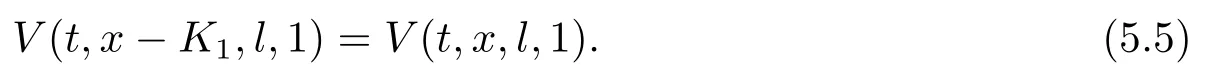
From(4.13)and (5.3),it then follows that

Similarly,we define pre-default utility loss as

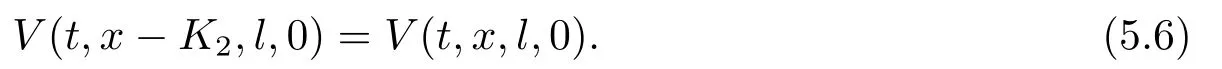
From (4.20)and (5.4),it then follows that

The loss functionK1,K2measures the utility loss of the AAI when she adopts the suboptimal strategy(t).

6.Sensitivity Analysis

In this section,we analyze the impact of parameters and model uncertainty on optimal investment and reinsurance strategies by some numerical examples.We suppose that the claim sizes are exponentially distributed with the parameterθ=2.In the following analysis,unless otherwise stated,the basic parameters are listed below:

At first,in Fig.1,we know thatβ∗1(t)decreases with the model uncertainty coefficientυ2and risk aversion coefficientγ,which indicate that the insurer will pay less money to invest in stock market whenυ2orγbecomes larger.Similarly,β∗2(t)decreases with the model uncertainty coefficientυ3and risk aversion coefficientγ.From Figs.3 and 4,we can see that the optimal portfolio strategyβ∗1(t)andβ∗2(t)are decreasing while the value ofλincreases.This is also to be expected,because a greater value ofλimplies a greater value of the expected jump number,the investor would rather invest less money to the risky asset.For strategyβ1andβ2,we can find that whenλ1<λ2,the value ofβ1is larger thanβ2,and vice versa.This implies that the values of the optimal portfolio strategy are sensitive to the counting processes.

As described in Fig.5,the optimal wealth invested in the defaultable increases when the loss rateςdecreases.On the contrary,the insurer will invest more money in the defaultable bond with higher credit spreadδ.Note thatυ6reflects the insurer’s attitude towards the jump risk caused by default,we can find that a largeυ6induces less wealth invested in the defaultable bond,which is well depicted in Fig.6,and also shows that the robust optimal investment strategyβ∗3(t)decreases with respect to the default intensityhP.In fact,the probability of default will be larger when the default intensityhPis higher,and the counterparty risk of the defaultable bond will undermine its investment grade and thus make it less attractive to the insurer.

Next we discuss the effect ofυ1,γon the strategyα(t)over time respectively.Sinceυ1reveals the ambiguity aversion for jump risk caused by claim.As is illustratedwith higherυ1andγ,the insurer has lower risk exposure in insurance market,so as to less amount of money will be paid to purchase reinsurance.We also find that the robust optimal reinsurance strategies under the generalized mean-variance premium are very different from that under the variance premium principle.

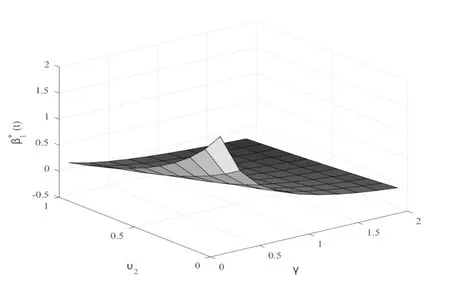
Fig.1 Effect of γ and υ2

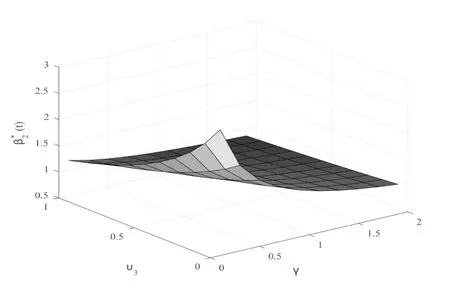
Fig.2 Effect of γ and υ3

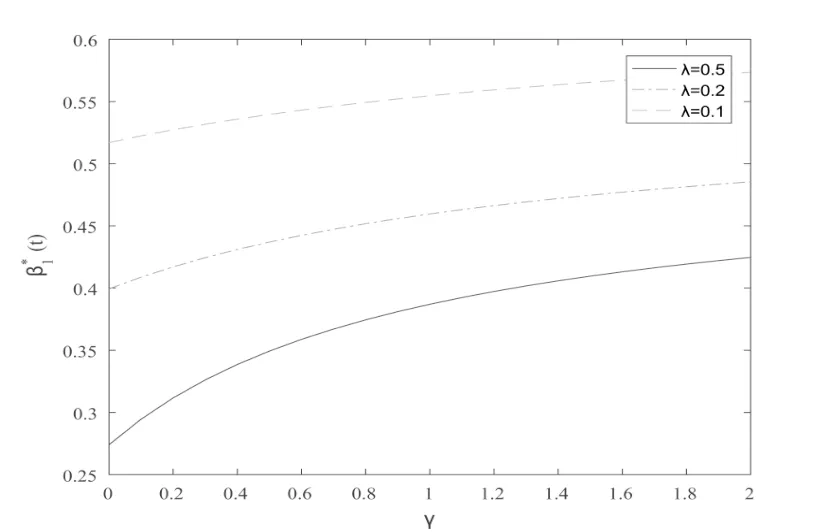
Fig.3 Effect of γ and λ

Fig.4 Effect of γ and λ

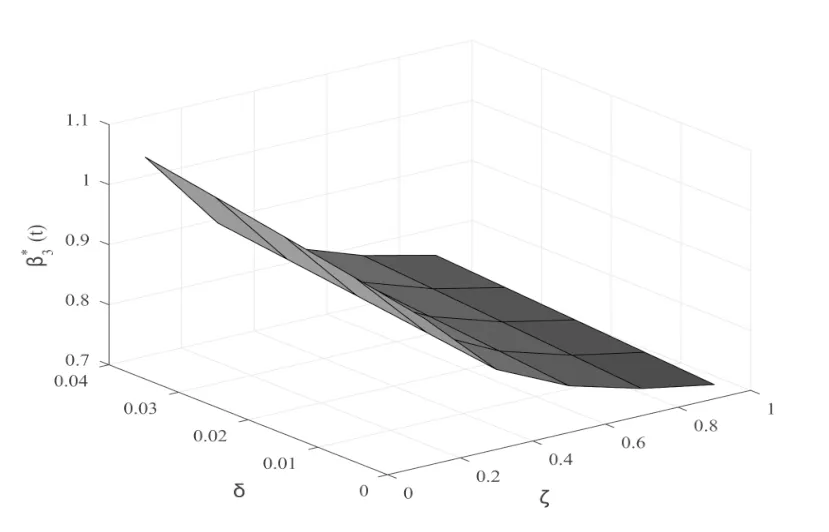
Fig.5 Effect of ς and δ

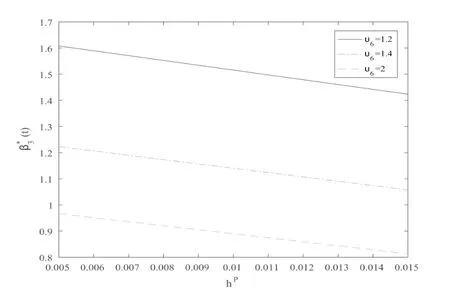
Fig.6 Effect of hP and υ6