混合系数线性模型参数的广义Liu估计
2021-04-16蔡择林陈金阳江秉华
蔡择林,陈金阳,江秉华
(1.湖北师范大学数学与统计学院,湖北 黄石435002;2.重庆三峡学院数学与统计学院,重庆404130)
1.引言
考虑如下混合系数线性模型

其中x(t)=(x1(t),x2(t),...,xp(t))T,y(t)=(y1(t),y2(t),...,yq(t))T是t的已知向量函数,a是p×1的固定系数向量,β是q×1的随机系数向量,且β ∼(b,Σ).
现对m个样品,分别在tij(ti1
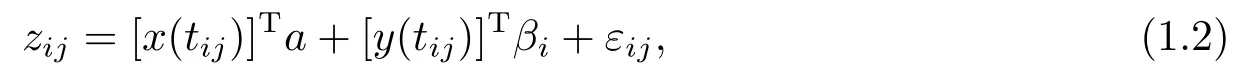
这里的βi和εij分别是每个样品的随机系数和每次测量的误差,βi与εij独立,且
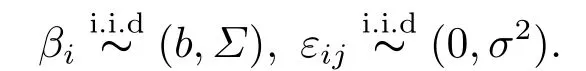
若记zi=(zi1,zi2,··· ,zini)T,εi=(εi1,εi2,··· ,εini)T,

则可得

设Ci=(Xi,Yi),d=(aT,bT)T,ei=Yi(βi −b)+εi,则式(1.3)变为
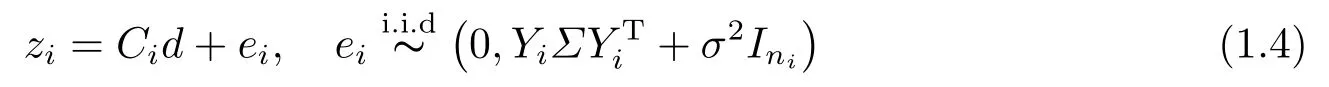
进一步,记z= (zT1,zT2,··· ,zTm)T,e= (eT1,eT2,··· ,eTm)T,C= (CT1,CT2,··· ,CTm)T,D=diag(D1,D2,··· ,Dm),其中Di=YiΣYTi+σ2Ini.则可将式(1.4)写成

这里还要求rank(Xi)=p,rank(Yi)=q,
混合系数线性模型在经济分析、可靠性退化分析以及生物学等领域有着广泛的应用,许多学者研究了该模型的参数估计问题[3−10].基于模型(1.5),庄东辰等给出了d的LS估计[3],LS估计虽然无偏,但当系数阵接近病态时,LS估计的均方误差过大,稳定性不好.针对此情况,郭金亚等提出了一种有偏估计,即Liu估计[4].本文改进Liu估计后给出了广义Liu估计,并证明了在均方误差意义下,此类估计分别优于最小二乘估计、Liu估计,最后讨论了参数的选取问题.
本文符号说明:对于矩阵A和B,A ≥0表示A为半正定矩阵;A >0表示A为正定矩阵;A ≥B表示A ≥0,B ≥0且A −B ≥0;A>B表示A ≥0,B ≥0且A −B >0.
2.广义Liu估计
模型(1.5)的典则形式为

其中L=CQ,r=QTd,QTCTCQ=Λ=diag(λ1,λ2,...,λg).
庄东辰等给出了d的LS估计:=(CTC)−1CTZ,其典则形式为=Λ−1LTZ.
郭金亚等给出了d的Liu估计:
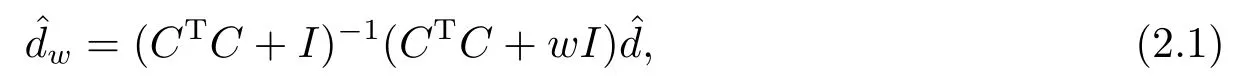
本文将Liu估计(2.1)做如下拓广,称
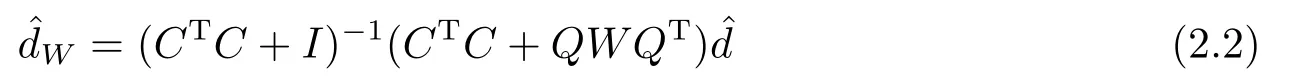
为d的广义Liu估计.其典则形式为= (Λ+I)−1(Λ+W),其中W为对角矩阵且满足0≤W= diag(w1,w2...,wg)≤I.显然,当W=wI,0≤w ≤1时即为普通Liu估计(2.1).特别地,当W=I时即为LS估计.
3.广义Liu估计的性质
定理3.1估计的期望向量和协方差矩阵分别为
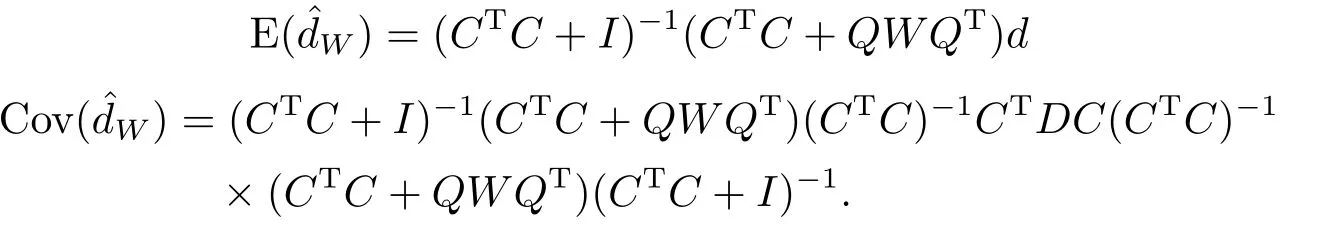
定理3.2估计是有偏、压缩估计,即等号成立当且仅当W=I.
证因为故有:
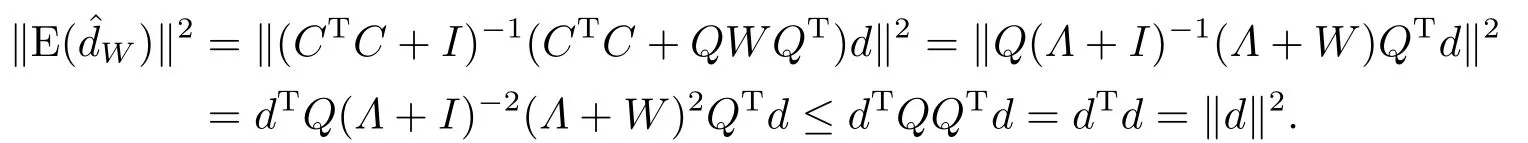
定理3.3存在0≤W∗ 证显然, 其中M= diag(M1,M2,...,Mm)= diag(Y1ΣYT1,Y2ΣYT2,...,YmΣYTm),lj= (LTML)jj ≥0, 对二次函数fj(wj)=(1+kjλj)w2j+2(1−kj)λjwj+λ2j+kjλj,容易解得wj的最优值为 显然0≤W∗=diag(w∗1,w∗2,...,w∗g) 于是定理得证. 定理3.4设Liu估计的均方误差 当w=w0时达到最小,则存在0≤W∗ 证如下选取参数w∗j 显然0≤W∗= diag(w∗1,w∗2,...,w∗g) 从而 所以定理得证. 此处介绍极小化均方误差的无偏估计法,由 可得 可构造均方误差 的一个无偏估计如下: 模拟中,取p=q= 1,m= 1,n1= 2.假设时刻tij服从[0,1]上的均匀分布,由MATLAB生成随机数t11= 0.8147,t12= 0.2785.取(1,2)T,β1∼N(2,1),ε1∼N(0,I2). 当W=I时,=67.6274,当W=diag(0.1,0.2)时,比较知:即广义Liu估计优于LS估计. 当0≤w ≤1时,通过对w的取值得到下表: w 0.3 0.4 0.5 0.6 0.7 0.8 MSE(dw)30.0399 34.4668 39.2080 44.2634 49.6331 55.3170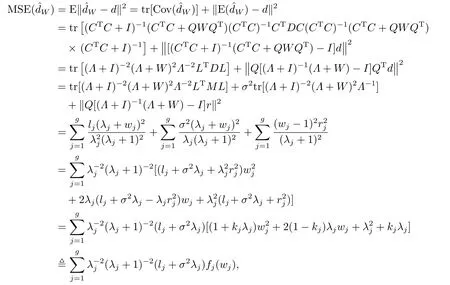
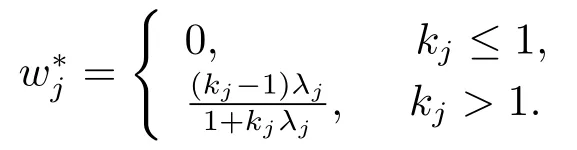
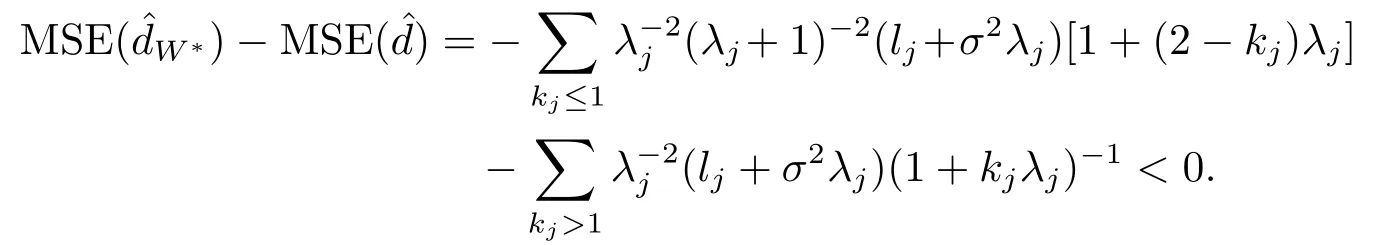
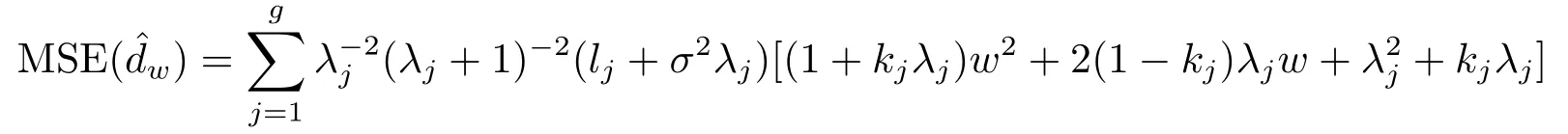
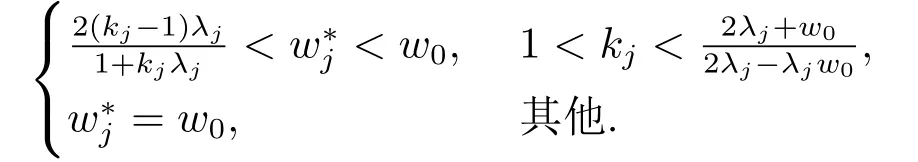
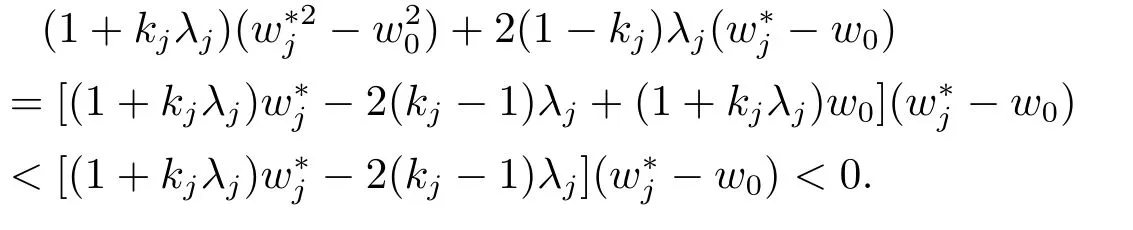
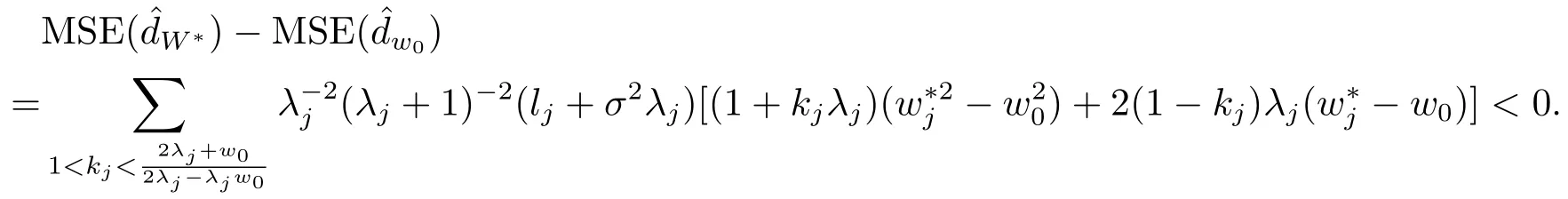
4.参数的选取
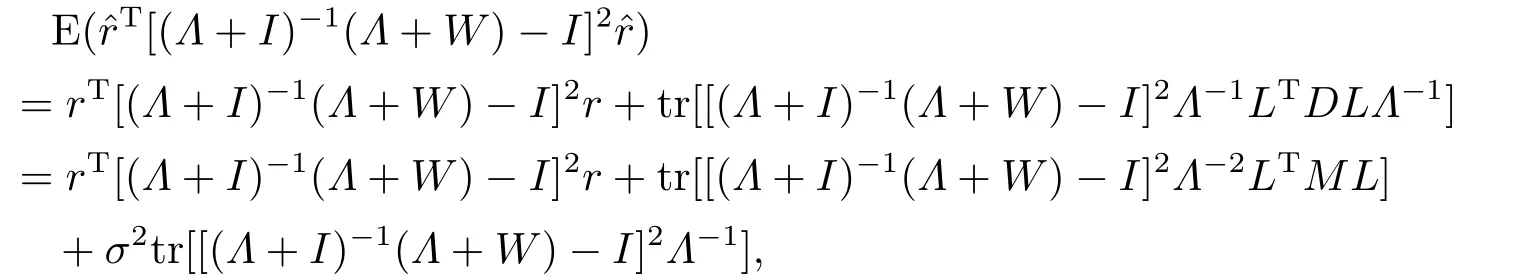
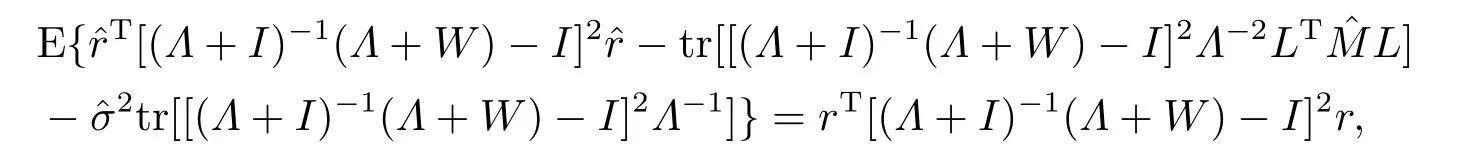
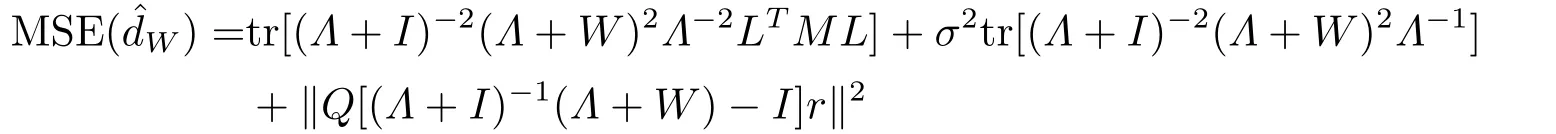
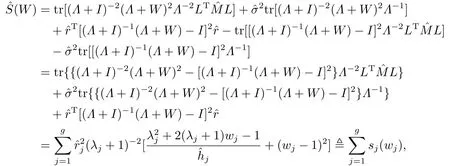
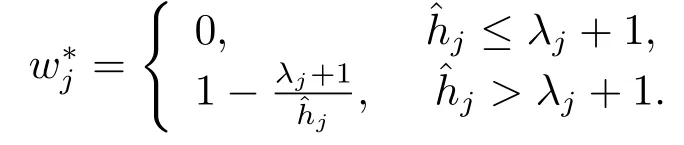
5.模拟算例

