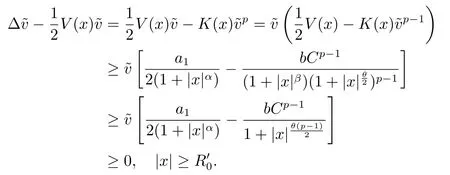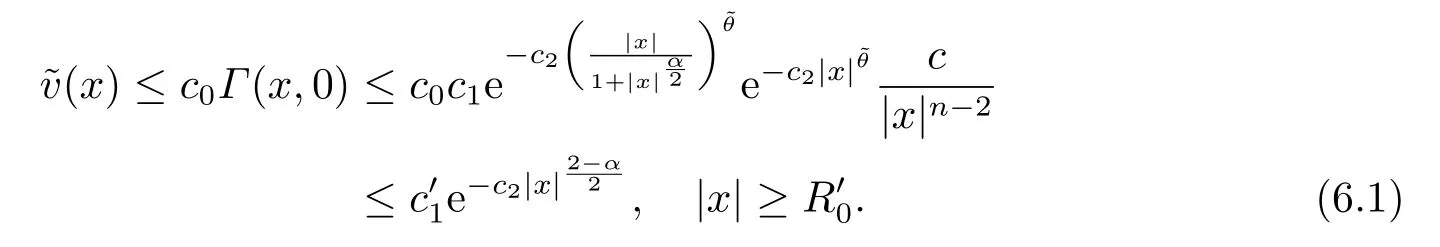Ground States of Nonlinear Elliptic Equations:A Dynamical Approach
2021-04-16YANXuntian闫训甜SUNChunyou孙春友
YAN Xuntian(闫训甜),SUN Chunyou(孙春友)
(1.School of Science,Qingdao University of Technology,Qingdao 266525,China;2.School of Mathematics and Statistics,Lanzhou University,Lanzhou 730000,China)
Abstract: In this paper,we apply the ideas and methods of dynamical system theory to a class of nonlinear elliptic equation with subcritical exponent.We study the existence and asymptotic behavior of ground state solutions of stationary equations through the existence and structure analysis of attractors.The detailed application of this method not only needs the innovation in theory and application,but also provides new ideas and methods in the related fields,especially promotes the development,in both theory and application,of nonlinear analysis and infinite-dimensional dynamical systems.
Key words: Elliptic equation;Dynamical system;Ground state; ω-Limit set
1.Introduction and Main Results
In this paper,we consider the existence of ground states for the elliptic equation:
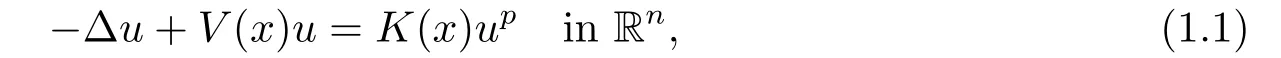
(V)There exista1,a2>0 andsuch that

(K)There existb>0 and 0<β <αsuch that

A solution of Eq.(1.1)is called a ground state if it is a non trivial solution which minimizes the energy functional.WhenV ≡1,it is well known that (1.1)has a ground state solution,meaning a positive solution decaying exponentially to 0 near infinity.The problem of looking for ground state solution is a very classical problem.It has been introduced by Coleman,Glaser and Martin[6],and reconsidered by Berestycki and Lions[3]for a class of nonlinear equation including the Schrödinger’s one.Later the existence and profile of ground state solutions have been studied for a plethora of problems by many authors.[1,11,20]
Many researchers deal with the steady-state problems usually use the classical variational methods,which initiated by Rabinowitz[14].The critical points of the corresponding Euler-Lagrange functional are precisely the weak solutions of the problem.The main theoretical basis is the famous mountain-pass theorem (or linking theorem,fountain theorem),concentration-compactness principle,critical point theory and so on.To prove the solution is a ground state mainly use constrained minimization technique.[1,11−12,20]
As we know,steady-state problems are the trivial case of dynamical systems,that is,the systems tend to stationary,then the solutions tend to a equilibrium as timet →∞.Based on this,we use dynamical systems theory to deal with elliptic problems.
In 2002,Souplet and ZHANG[15]developed a dynamical approach to an elliptic equation with decaying potentials of linear term.They showed that positive solutions of the elliptic equation can be got from global solutions of the corresponding evolution equation ast →∞by means of constructing attracting sets.This method not only extends the horizon of research on steady-state equations but also promotes evolution equations development.[4−5,9]
Inspired by [15],we consider the decaying potentials of both linear term and nonlinear term.About potentials of elliptic problems,authors in[2,20]assumed that potential functions between two positive constants or have a positive below bound,that is

In 2005,Ambrosetti,Felli and Malchiodi[1]first proposed the case lim|x|→∞V(x)=0.Later many researchers considered the decaying potentials by variational way.[11−12]However,authors in[12] argued that:
The range ofαin our condition (V)leads toα <2,hencedecays slowly.Then the positive solution of (1.1)decays exponentially to zero near infinity,which means the existence of ground state.Corollary 1.2 in [18] shows that all positive solutions of (1.1)blow up in finite time with the assumptionα >2 andSo,our condition (V)is sharp.
Now,we convert (1.1)to the corresponding parabolic equation

First,we prove that (1.2)admits global positive solutions under our conditions (V)and (K).Then we show that ifV(x),K(x)andu0are radial,some global solutions haveω-limit sets containing a positive equilibrium.Finally,we employ a new technique to explain that the positive solution is a ground state.
It is well known that there exist choices ofu0for which the corresponding solutionsu(t;u0)tend to 0 ast →∞;and other choices for whichu(t;u0)blows up in finite time(i.e.solutions do not exist in the large).The behavior that neither tends to zero nor blows up in finite time is called “borderline”behavior.However,any nonzero equilibrium state is dynamically unstable,then we have two stable states,u ≡0 andu ≡∞.So,in the beginning,we need to indicate thatu ≡0 must be stable in a suitable topology.It is not straightforward because,due to the decay ofV(x)andK(x),the linear termV uand the nonlinear termKupare not strongly coercive.Another trouble is,due to the lack of compactness,it is not clear if theω-limit set (in the same topology)is non-empty.
To circumvent these difficulties,we need to work in adapted weightedL∞spaces and to use suitable comparison arguments and energy estimates,as well as a priori bound on global solutions to (1.2).Now we introduce the following Banach space:For eachk ≥0,
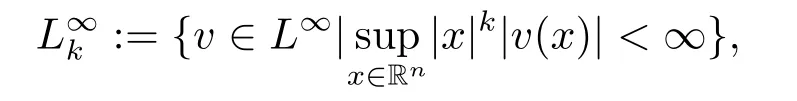
which is endowed with the norm

And one closed subspace

Here and below,we simply writeLq:=Lq(Rn)(1≤q ≤∞)which denotes the usual Lebesgue space,andW1,q:=W1,q(Rn)(1≤q ≤∞)which denotes the usual Sobolev space,with norms∥·∥qand∥·∥W1,qrespectively.DenoteH1:=H1(Rn)=W1,2(Rn)with norm∥·∥H1.
Recall that,by the standard theory,for allu0∈L∞,(1.2)has a unique,maximal in time,classical solutionu=u(x,t).The solution at timetbelongs toL∞and will be denoted byu(t;u0)orS(t)u0,or simplyu(t)if no confusion arises.Ifuis of mixed sign,thenupis understood as|u|p−1u.Moreover,u0≥0 impliesu ≥0 (by the maximum principle).We denote byT(u0)∈(0,∞] the maximal existence time ofu(.;u0).IfT(u0)<∞(i.e.the solution is blow up in finite time),then(i.e.the solution is global),we define theω-limit set ofu:
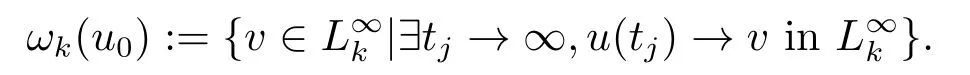
Now we state our main results.We use the following theorem to show that Eq.(1.1)has a positive solution.
Theorem 1.1Suppose (V)and (K)hold.Assume thatV(x)=V(|x|)andK(x)=K(|x|)are radially symmetric.Letand1withϕ ≥00,ϕradially symmetric.Then there existsλ∗>0 such thatT(λ∗ϕ)=∞andωk(λ∗ϕ)contains a positive equilibrium(x)of (1.2).
Incidentally,we study the asymptotic behavior of global positive solutions of Eq.(1.1)by the following theorem.
Theorem 1.2Under the assumptions of Theorem 1.1,Eq.(1.1)has a global positive solutionv.In particular,it is radial and satisfies
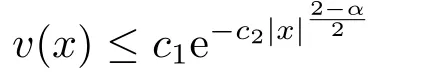
for somec1,c2>0.
2.Global Existence for Small Initial Data
In this section,we use the following lemma to show that when the initial data small enough,Eq.(1.2)has a global solution.
Lemma 2.1Suppose (V)and (K)hold.LetThen there existδ >0 andC ≥1 such that for allu0∈L∞ksatisfying∥u0∥∞,k ≤δ,the corresponding solutionuof (1.2)is global in time and satisfies
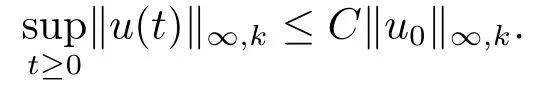
ProofWithout loss of generality,assumeu ≥0.LetforA>0,then
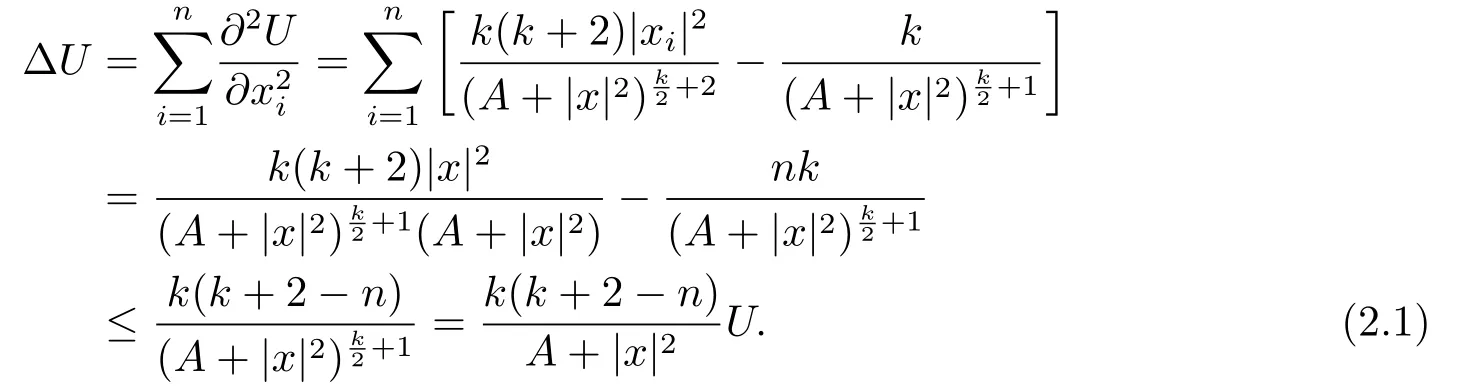
Since 0≤α<2,we can choosea1andA=A(a1,α,k)large enough such that
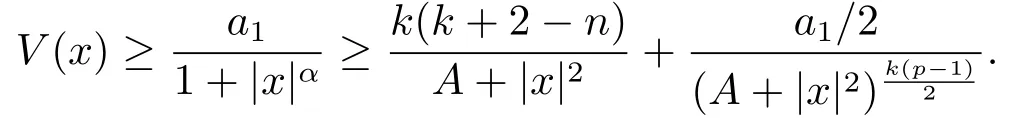
Then

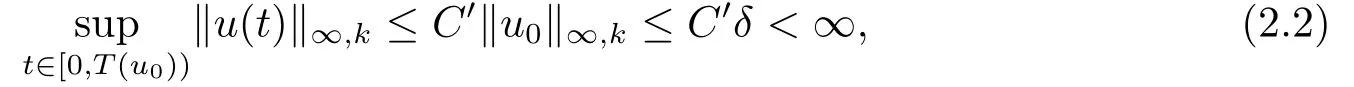
that is,T(u0)=∞.
By Lemma 2.1,we can immediately deduce thatu ≡0 is stable,that is,u ≡0 is an isolated solution of (1.1).
Corollary 2.1Under the assumptions of Lemma 2.1,ifu0,then0.
Proof(2.2)also implies thatThen for allxandt >0,taking 0<δ By the maximum principle(see also[13],Chapter 3,Theorem 12),Therefore,ifu0,then by Proposition 2.1 in [15], In this section,we give some energy estimates for Eq.(1.2),these results will play a key role in the following discussion. Foru0∈L∞∩H1,it is well known thatu ∈C([0,T(u0));H1).The energy of (1.2)can be written as By Green’s identity and (1.2),we have Multiplying both sides of (1.2)byuandutrespectively,and then integrating on Rn,we have (3.2)and (3.3)implies that ifT(u0)=∞,thenE(t)≥0 for allt ≥0 (otherwise the solution must blow up in finite time[8]. And since IfV(x),K(x)andu0are radially symmetric,settingr:=|x|,we get First of all,we illustrate that when the solution of (1.2)is global,elements in theω-limit set are equilibria. Lemma 4.1Letu0∈L∞∩H1.IfT(u0)=∞,then for eachk ≥0,theω-limit setωk(u0)consists of equilibria. ProofAssume∈ωk(u0),then there existstj →∞such thatu(tj)→inL∞k.Fixingt>0 and by the continuity of semigroup,we have Then for eachR0>0,by Schwarz’s inequality and (3.4),we have Hence Next,we establish the compactness property inL∞k,which means that the attracting setωk(u0)is not empty. Lemma 4.2Suppose (V)and (K)hold.Letu0∈L∞∩H1and assumeT(u0)=∞.In addition assume thatV(x),K(x)andu0are radially symmetric and letThen the sequence{u(tj+τ)}is precompact inL∞kfor someτ >0,that isωk(u0)∅. ProofSetBy Young’s inequality,for eachξ >0,we have Then it follows from Gronwall’s inequality and (3.4)that Multiplying both sides of (1.2)byuand integrating,we obtain,forT >0, Then TakingT ≥1,we have Particularly,for each integerj ≥1,there existstj ∈[j,2j] such that And sinceE(tj)≤E(0)≤C(∥u0∥H1),we also get Forn ≥3,sinceu(t)∈W1,2,standard Sobolev imbedding implies thatu(t)∈Lq1and∥u(t)∥q1≤C(n,2)∥∇u(t)∥2for Forn=2,by Poincaré’s inequality and Sobolev imbedding theorem,we have∥u(t)∥q2≤C∥u(t)∥H1≤C∥∇u(t)∥2. It follows from the regularity of semilinear heat equations (see [17],Proposition 2.2)that for allL >0,there existτ=τ(L)>0 andM(L)>0 such that for allt ≥0,∥u(t)∥q ≤L(q=q1ifn ≥3;q=q2ifn= 2)implies that∥u(t+s)∥q ≤2L(0≤s ≤τ)and∥u(t+τ)∥W1,q′ ≤M(L)(q ≤q′ ≤∞).Hence we have whereq ≤q′ ≤∞,j=1,2,.... Letr:=|x|.By the assumption,u(.,t)is radial and then.[16] Takingθ:=n −1and using Hölder’ inequality,we have Then by (3.1)and (3.5),we obtain Thus Since,(4.2)means that (1+|x|k)|u(x,t)|→0 as|x|→∞for allt>0.(4.1)and (4.2)implies that{u(tj+τ)}is precompact inL∞k,that is,ωk(u0)∅. In this section,we prove that zero is not contained in theω-limit set,and this result relies on uniform a priori estimate for global solutions of (1.2).To elucidate it,we use a classical“blow up”argument introduced in[8].At the end of this section,we give the proof of Theorem 1.1. Set By Corollary 2.1,D0is well defined and contains an open neighborhood of 0 in.So we can describeD0as another form In the first place,we use the following lemma to show thatD0is open inL∞k,0. Lemma 5.1(Continuous dependence inL∞k)Foru0,∈L∞kand all 0<τ Furthermore, ProofSinceτ Takingγ1:=QM′p−1+1+Pandz(x,t):=e−γ1tu(x,t),we observe that The maximum principle implies thatz(x,t)≤et(∆−1)u0.And then by Proposition 2.1 in[15],we get that is,∥u(t)∥∞,k ≤Ceγ1τ∥u0∥∞,kfor 0≤t ≤τ.Hence (5.1)holds. On the other hand Takingγ2:=Qp(M′+1)p−1+1+Pand repeating the previous argument,we get∥w(t)∥∞,k ≤Ceγ2τ∥u0−∥∞,kfor 0≤t ≤τ.Hence (5.2)holds. Now,letu0∈D0and assume that∥−u0∥∞,kis sufficiently small.Lemma 5.1 implies that0∈D0.ThusD0is open. In the second place,putλ∗:=sup{λ>0|λϕ ∈D0}(hereϕis given by the assumption in Theorem 1.1).According to the discussion in Section 2,we can immediately get 0<λ∗<∞.By the definition of supremum,there exists a sequence{λj}withλjϕ ∈D0,such thatλj →λ∗asj →∞andT(λjϕ)=∞.Meanwhile,the openness ofD0means thatλ∗ϕ /∈D0.To prove 0(λ∗ϕ),it is sufficient to showT(λ∗ϕ)=∞.This process needs to use the following uniform a priori estimate and a blow up argument. Lemma 5.2(Uniform a priori estimate for global solutions)IfT(u0)=∞,then whereC(s)is bounded forsbounded. ProofBy the standard local theory,there existsτ=τ(∥u0∥∞)>0 such that Arguing by contradiction,we assume that there exists a sequence{uj}of global solutions and timesj ≥0 such that Choose(xj,tj)∈Rn×(0,sj]such thatWe can assume (by choosing subsequence)xj →x∗asj →∞.And by (5.4),we may assumetj ≥τ.Letand define the scaled (“blow up”)function Thensatisfies By using the interiorLqparabolic estimate (see [10],Proposition 7.18),standard imbedding and a similar proof to [8],it follows that (some subsequence of)converges,uniformly on compact subsets ofX:=Rn×(−∞,0],to a bounded solution≥0 of On the other hand,for eachm>0,by (3.4)and our contradictory hypothesis,for alljlarge enough, For allX′ ⊂⊂X,we may assume,taking yet another subsequence if necessary thatinL2(X′),which implies thatThus∂s≡0.Therefore which contradicts a Liouville theorem (see [7],Theorem 1.1). Using Lemma 5.2,we immediately get Proof of Theorem 1.1Firstly,sinceV(x),K(x)andλ∗ϕare radially symmetric,by Lemma 4.2,ωk(λ∗ϕ)∅.Secondly,by Lemma 4.1,ωk(λ∗ϕ)contains an equilibrium≥0 (sinceλ∗ϕ ≥0).Thirdly,by the discussion in Section 5,0/∈ωk(λ∗ϕ).Finally,by the strong maximum principle,>0.So far,we can conclude thatis a positive solution of (1.1). In this section,we describe the asymptotic behavior of the global positive solution of Eq.(1.1).In other words,∆u −u+up=0 has a ground state solution. Proof of Theorem 1.2From the proof of Theorem 1.1,we can easily verify thatis a global positive solution of (3.1)and it is also radially symmetric.Moreover,the estimation(4.2)yieldsandThen there existsR′0>0 such that Letu0(x)=Γ(x,0),whereΓis the Green’s function of the Schrödinger operatorSinceVandΓvanish near infinity,by the maximum principle,there existsc0>0 such that(x)≤c0u0(x)for|x| ≥R′0.Whenn ≥3,by Corollary 1 in [19],there existc1,c2>0 such that for allx,yandit holds Takingy=0 in the above inequality,we have (6.1)also holds forn=2.This reveals that(x)vanishes exponentially to 0 near infinity.
3.Energy Estimate

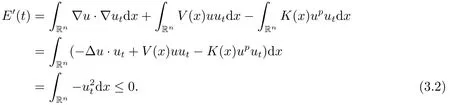

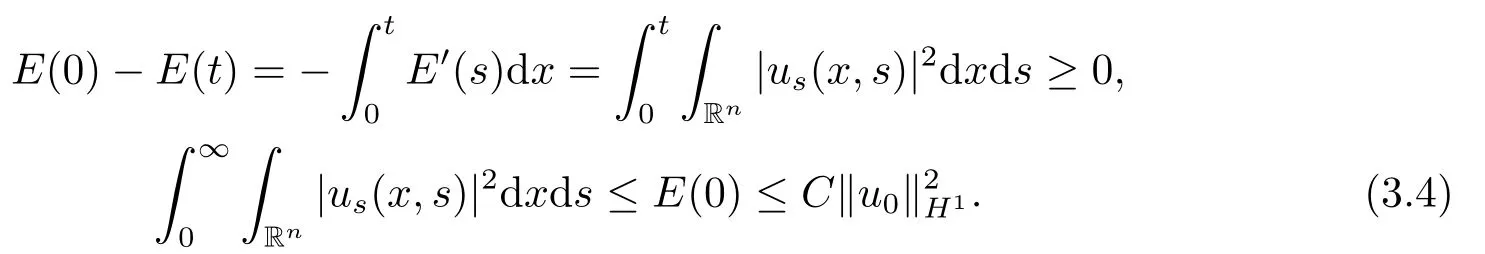
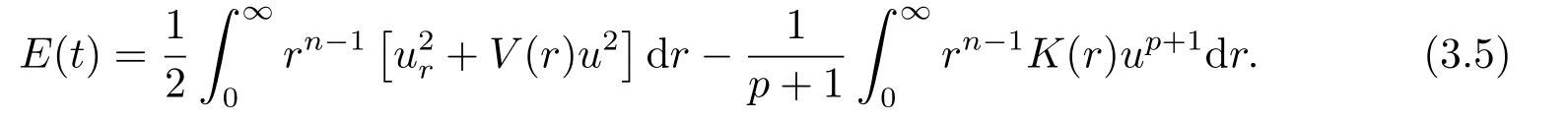
4.Non-Emptiness of ω-Limit Set




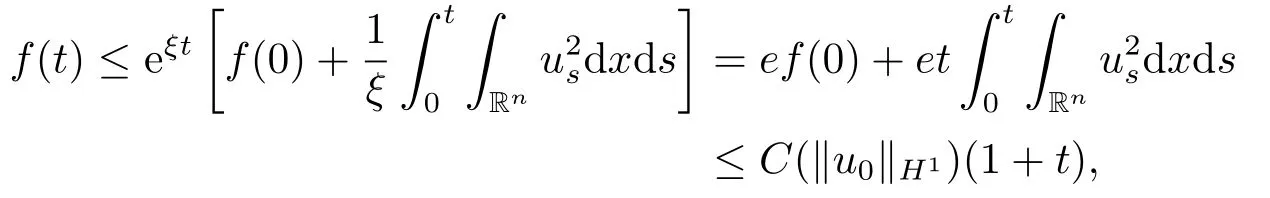


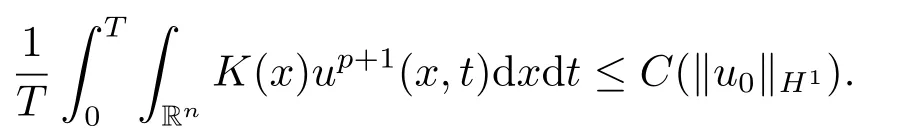
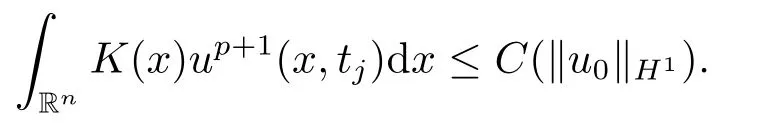

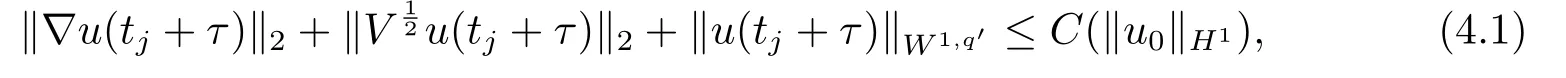
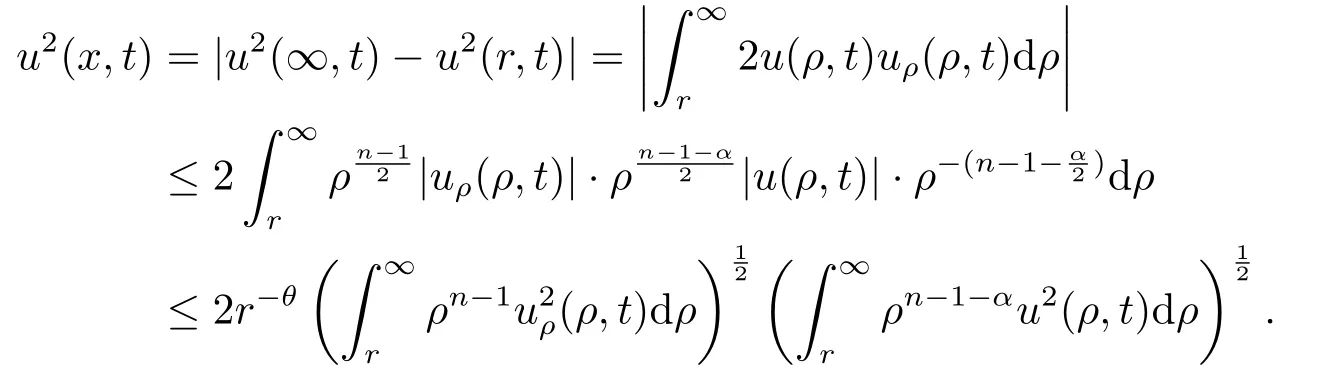
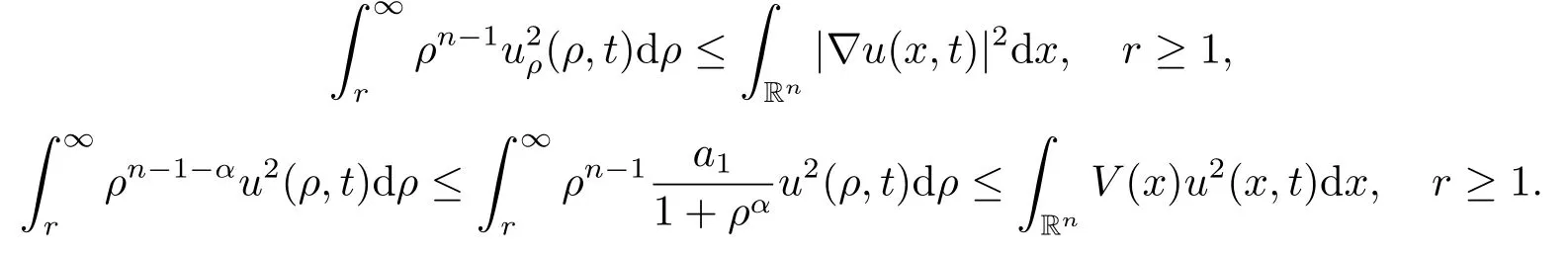
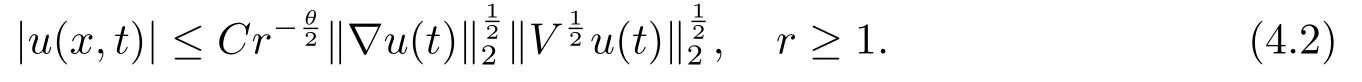
5.Zero is Excluded from ω-Limit Set
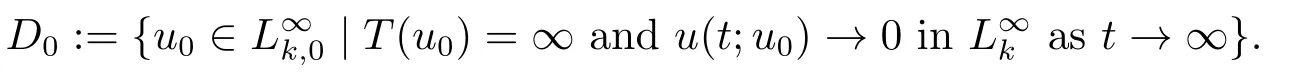


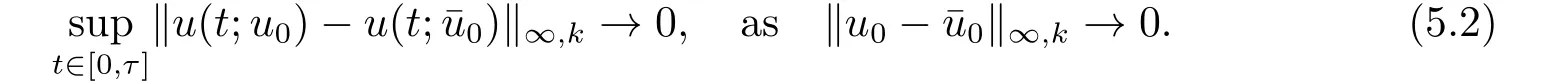
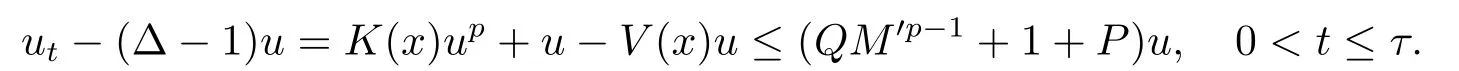
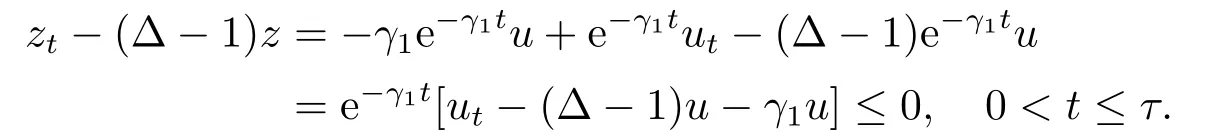
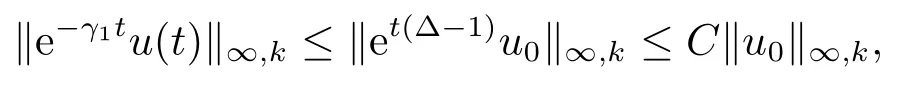
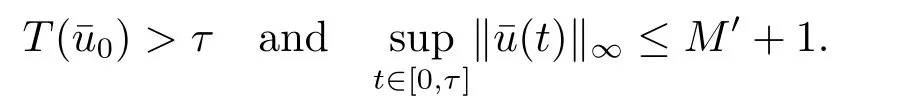



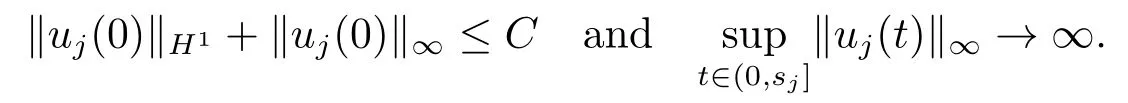
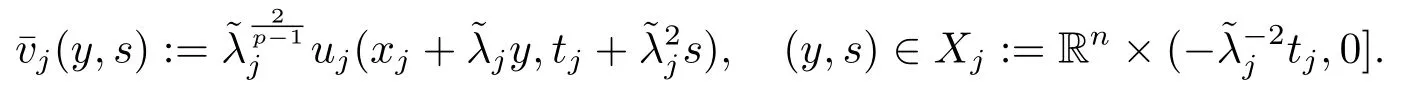
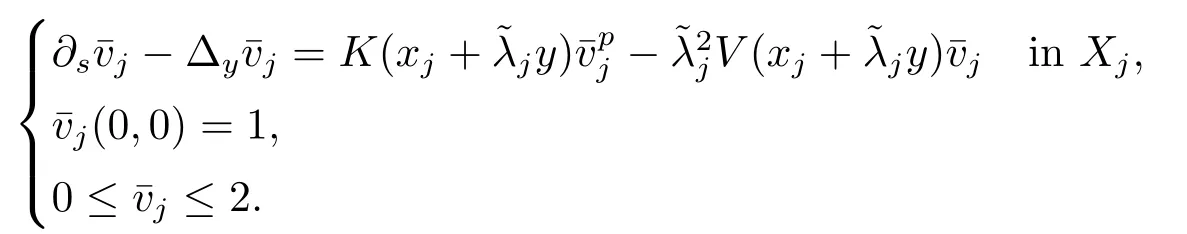
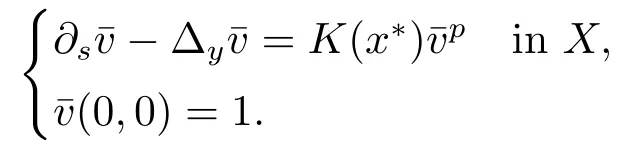
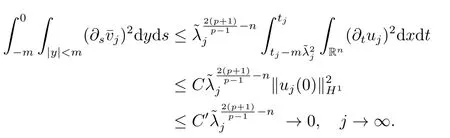
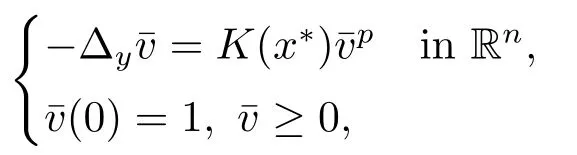
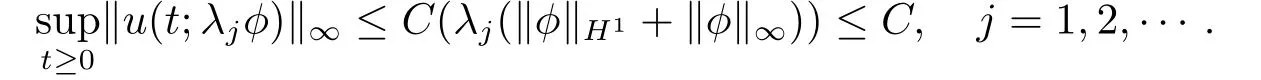
6.Asymptotic Behavior