冲击泡沫金属强化换热研究
2021-04-16许改云
许改云
(太原学院,山西太原 030000)
射流冲击强化换热已广泛应用于平板玻璃回火、金属薄板淬火、退火,纺织品或纸张干燥,燃气轮机叶片冷却及电子产品冷却等技术中。在这种换热方式中,气体或液体在压差作用下通过一个圆形或窄缝形喷嘴垂直地喷射到被冷却的表面上,从而使受到直接冲击的区域产生强烈的换热效果。泡沫金属是一种在金属基体中形成无数气泡的多孔性金属材料,又称多孔性泡沫金属,由于它具有金属特性和非金属的一些特殊物理性能,因而得到国内外的普遍关注。近年来,泡沫金属作为新型金属材料开始迅速发展,以其有比重小、刚度大、比表面积大的优点,不断有学者关注泡沫金属在强化换热应用方面的研究,基于泡沫金属的各种特性,被广泛应用于各个领域,利用其优异的热物理性能,可用来强化换热,制作换热器和散热器。计算流体动力学(CFD)是通过计算机数值计算和图像显示,对包含有流体流动和热传导等相关物理现象的系统所做的分析。CFD的基本思想可归结为:把原来在时间域及空间域上连续的物理量的场,如速度场和压力场,用一系列有限个离散点上的变量值的集合来代替,通过一定的原则和方法建立起来关于这些离散点上场变量之间关系的代数方程组,然后求解代数方程组获得场变量的近似值。
1 物理模型
图1显示,射流冲击泡沫金属强化换热的物理模型。在模型中,泡沫金属的长l=12cm,高度h是变量,取值分别为2cm、4cm、6cm,流道总高度定量H=8cm,喷嘴宽度W=0.7cm,喷嘴到泡沫金属上表面的距离C,其值随泡沫金属高度的变化而变化, 流道总长度L=50cm,喷嘴雷诺数Re=7000,对应的流速v=14.61m·s-1,冲击介质为空气,温度为T=300K,泡沫金属下表面为热源,其热流密度q=10kW·m-2,其他表面为绝热面。采用有限体积法的基本思想进行分析,通用控制方程有连续性方程、动量守恒方程、能量守恒方程,基于局部热平衡假设模型和SLMPLE算法进行速度、温度和压强的耦合,为保证计算结果的精确性,采用二阶迎风格式。泡沫金属区域和流体区域的离散网格尺寸分别为0.2mm和0.4mm。泡沫金属物性参数如表1所示:

图1 物理模型

表1 泡沫金属物性参数
2 数学模型
2.1 控制方程
泡沫金属区域为多孔介质区域,认为固体和流体存在能量平衡,动量方程采用Darcy-Brinkman-Forchhermer模型:
连续性方程:

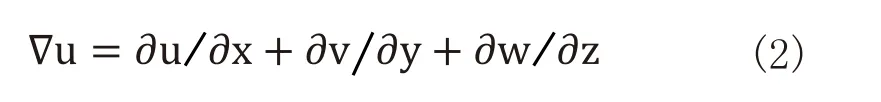
动量守恒方程:

能量守恒方程:
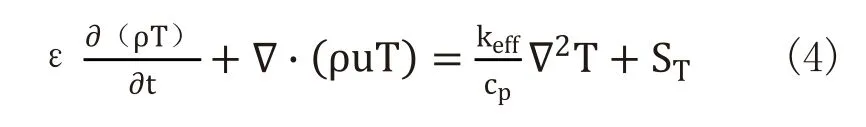
上式中t为时间;u为速度矢量;ρ,μ,T分别为流体的密度,运动粘度和温度;ε,K,分别为泡沫金属的孔隙率、渗透率;cF为 Forchhermer系数;keff,cp, 分别为泡沫金属区域有效导热系数和热容;ST,Si为源项。
2.2 参量方程
泡沫金属丝df与 孔径dp的关系式为:

泡沫金属渗透率K可由下式确定:
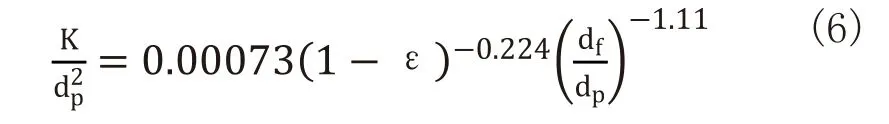
惯性系数F可由下式确定:

泡沫金属区域的有效导热系数keff、 流体有效导热系数kfe、 固体骨架有效导热系数kse的关系为:

泡沫金属孔隙比表面积asf:
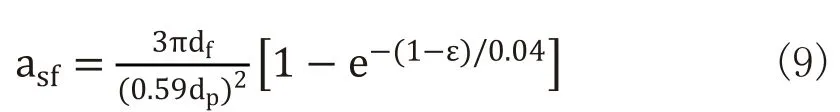
摩擦系数的表示关系:

上式中kfe,kse,kf,ks分 别为流体的有效导热系数,固体骨架有效导热系数,流体的导热系数和固体骨架导热系数;asf为泡沫金属孔隙的比表面积,τw是表面剪切应力。
3 结果与分析
3.1 泡沫金属层高对流线的影响
图2显示,泡沫金属层高对冲击形成流线的影响。气流从喷嘴进入,垂直冲击在泡沫金属上表面,进入泡沫金属层后气流开始发散,部分气流沿垂直换热面方向继续流动,另一部分气流由于受到泡沫金属内部阻力的作用开始沿流道方向流动,最终从出口流出。由于喷嘴入口处气流流速较大,压强较小,而流道内流速较小,压强较大,从而就在入口附近形成气旋,泡沫金属层高不同,气旋的大小也不同,h=4cm时,气旋半径较大,h=6cm时,气旋半径较小,这是由于泡沫金属内部阻力影响气流的流动,致使流道内压强的不同分布,形成不同的气旋。
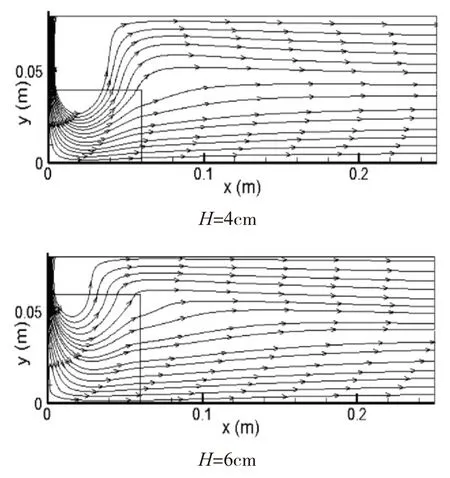
图2 泡沫金属层高对流线的影响
3.2 泡沫金属层高对换热系数的影响
图3显示,泡沫金属层高(h=2cm, 4cm, 6cm)不同,冲击泡沫金属在热源表面生成的换热系数。在h/H=0.25时,换热系数最大,h/H=0.75时,换热系数最小;在热源表面,止滞点(x=0cm)处换热系数最大,出现峰值,在止滞点(x=0cm)两侧,换热系数逐渐降低,且h/H=0.25时,换热系数变化速率最快,h/H=0.75时,换热系数变化速率最慢。这是由于,泡沫金属层高越小,冲击气流进入泡沫金属的阻力越小,越容易进入泡沫金属,流量越大,从而空气与热源换热越充分,使其带走更多的热量。而止滞点(x=0cm)处,气流冲击在热源表面,速度发生巨变,空气扰动最剧烈,换热更为充分。
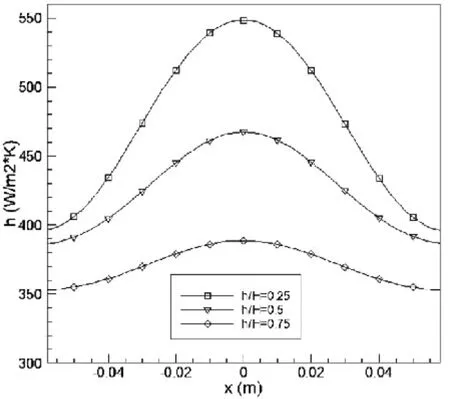
图3 泡沫金属层高度对换热系数的影响
图3显示,泡沫金属层高(h=2cm, 4cm, 6cm)不同,冲击泡沫金属在热源表面生成的换热系数。在h/H=0.25时,换热系数最大,h/H=0.75时,换热系数最小;在热源表面,止滞点(x=0cm)处换热系数最大,出现峰值,在止滞点(x=0cm)两侧,换热系数逐渐降低,且h/H=0.25时,换热系数变化速率最快,h/H=0.75时,换热系数变化速率最慢。这是由于,泡沫金属层高越小,冲击气流进入泡沫金属的阻力越小,越容易进入泡沫金属,流量越大,从而空气与热源换热越充分,使其带走更多的热量。而止滞点(x=0cm)处,气流冲击在热源表面,速度发生巨变,空气扰动最剧烈,换热更为充分。
3.3 泡沫金属材质对换热面Nu数的影响
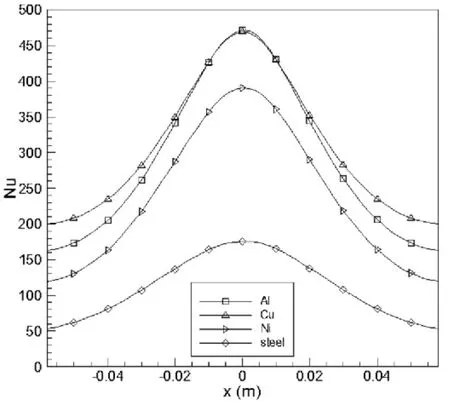
图4 泡沫金属材质对换热面Nu数的影响
图4显示,泡沫金属材质(Cu、Al、Ni、Steel)不同,冲击泡沫金属在热源表面生成的Nu数。在泡沫金属材质为铜时,换热表面的Nu最大,其次依次是铝、镍、钢,且止滞点(x=0cm)处,Nu数最大,出现峰值,换热效果最佳,沿气流流动方向,Nu数依次降低。这是由于当泡沫金属孔隙率ε=0.9,喷嘴Re=7000时,铜质泡沫金属的有效导热系数最大其值为13.07W/(m·K),而铝6.83W/(m·K), 镍3.11W/(m·K), 钢0.57W/(m·K),热量就更容易进入到铜泡沫金属的骨架内,气流在进入泡沫金属后更容易将热量带走,从而使其Nu数更大,换热效果最佳。
3.4 泡沫金属孔隙率对换热面Nu数的影响
图5显示,泡沫金属孔隙率(ε=0.7, 0.8, 0.9,0.93)不同,冲击泡沫金属在热源表面生成的Nu数。泡沫金属孔隙率ε=0.9,换热面Nu数最大,孔隙率ε=0.7,换热面Nu数最小,且在止滞点(x=0cm)处,换热面Nu数最大,出现峰值,在止滞点(x=0cm)两侧换热面Nu数逐渐降低。这是由于当泡沫金属材质为铜,喷嘴Re=7000时,泡沫金属孔隙率ε=0.9时,比表面和有效导热系数共同影响换热的作用更明显,使换热面Nu数越大,强化换热效果显著。

图5 泡沫金属孔隙率对换热面Nu数的影响
3.5 泡沫金属层高不同时,x=0cm等值线上的速度和温度分布
图6显示,泡沫金属层高(h=2cm, 4cm, 6cm)不同,在x=0cm等值线上的速度分布。在泡沫金属层h/H=0.25的条件下,速度变化速率大,近似于线性变化,进入泡沫金属的速度小,v=8m/s。随h/H的增大,速度变化率明显变化,泡沫金属层越高,在接近换热面的泡沫层内速度变化率越小,且进入泡沫金属的速度也随高度的增加而增大,在气流进入泡沫金属层的薄层内,速度有相似的变化率。这是由于气流在泡沫金属内的流动阻力与泡沫金属的厚度成正相关,泡沫层厚度越大,气流流动阻力越大。
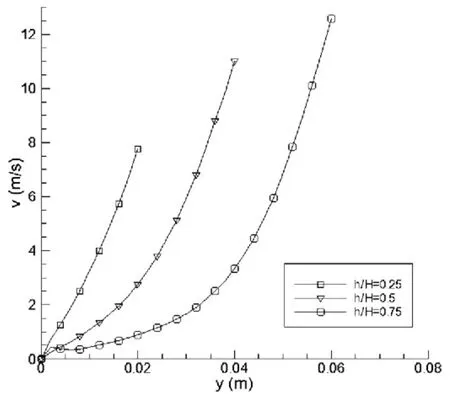
图6 泡沫金属层高不同时,x=0cm等值线上的速度分布
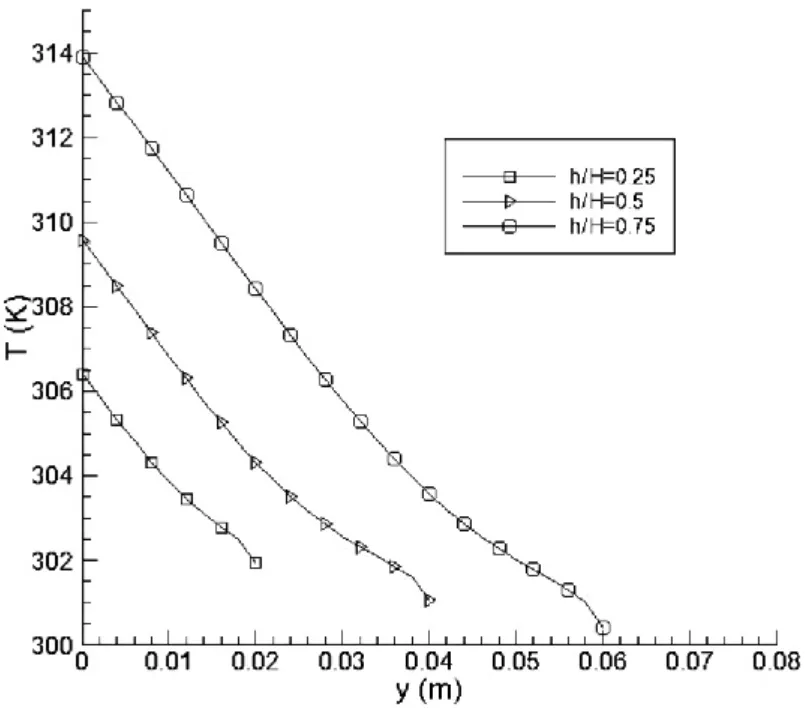
图7 泡沫金属层高不同时,x=0cm等值线上的温度分布
图7显示,泡沫金属层高(h=2cm, 4cm, 6cm)不同,在x=0cm等值线上的温度分布。随高度的增加,温度逐渐降低,且泡沫金属层越高,泡沫金属下表面温度越高,上表面温度越低,h/H=0.25所对应的温度分布,明显在其余两者温度分布的下面,这就说明,泡沫金属层的厚度相对低时,换热效果越显著。这是由于泡沫金属层越高,气流在其内部流动的阻力越大,到达下层后气流速度相对较小,与热源表面换热不充分,造成h/H越大,换热面温度越高的现象。而h/H越大,泡沫金属层温度越接近来流温度,从而使泡沫金属层上表面温度越低。
3.6 泡沫金属层高不同时,y=1cm等值线上的速度和温度分布
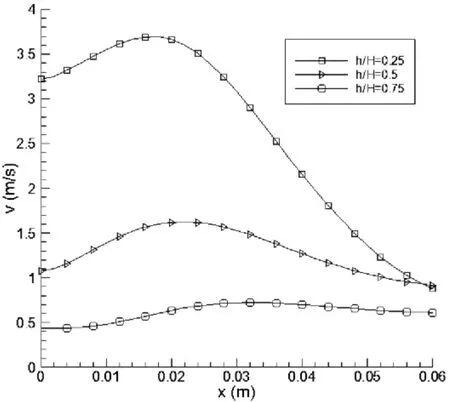
图8 泡沫金属层高不同时,y=1cm等值线上的速度分布
图8显示,泡沫金属层高(h=2cm, 4cm, 6cm)不同,在y=1cm等值线上的速度分布。h/H=0.25所对应的速度最大,沿流线方向速度逐渐增大,然后急剧减小,出现一个明显的峰值;而h/H=0.75所对应的速度曲线,沿流线方向略有增大,其变化趋势不明显。这就说明泡沫金属层高越小,y=1cm等值线上的速度越大,不同位置的速度变化也越大。这是由于泡沫金属层层高越小,气流在泡沫金属层的流动阻力越小,从而h/H=0.25所对应的速度最大。由于泡沫金属的高度与气旋的半径成负相关的关系,从而出现速度曲线峰值的现象,且随h/H的增大,峰值逐渐减小。

图9 泡沫金属层高不同时,y=1cm等值线上的温度分布
图9显示,泡沫金属层高不同(h=2cm, 4cm,6cm),在y=1cm等值线上的温度分布。每条温度分布曲线,其值在止滞点(x=0cm)处的温度最低,沿流线方向温度逐渐升高,h/H=0.25所对应的温度分布曲线最低,温度变化较大,h/H=0.75所对应的温度分布曲线最高,温度变化较小。这就说明泡沫金属层高度越小,换热效果越好。这是由于温度分布与速度分布成正相关的关系,速度越大,温度越低,热传递效果越显著。
3.7 固定泡沫金属层高时,不同等值线的速度和温度分布
图10显示,泡沫金属层高h=4cm时,y=0.5cm、y=1cm、y=2cm、y=3cm、y=4cm等值线处的速度分布。在x=0cm处,y=4cm所对应的速度最大,y=0.5cm所对应的速度最小,y=2cm、y=3cm、y=4cm所对应的速度沿流线方向逐渐降低,y=4cm所对应的速度变化最大,y=2cm所对应的速度变化最小,y=0.5cm、y=1cm所对应的速度先增大,然后逐渐减小,最终五条等值线对应的速度曲线逐渐接近重合。这是由于气流在冲击过程中流动阻力的不断变化影响了x=0cm处的速度分布,而在喷嘴附近气旋的存在,使五条等值线的速度呈现不同的分布。
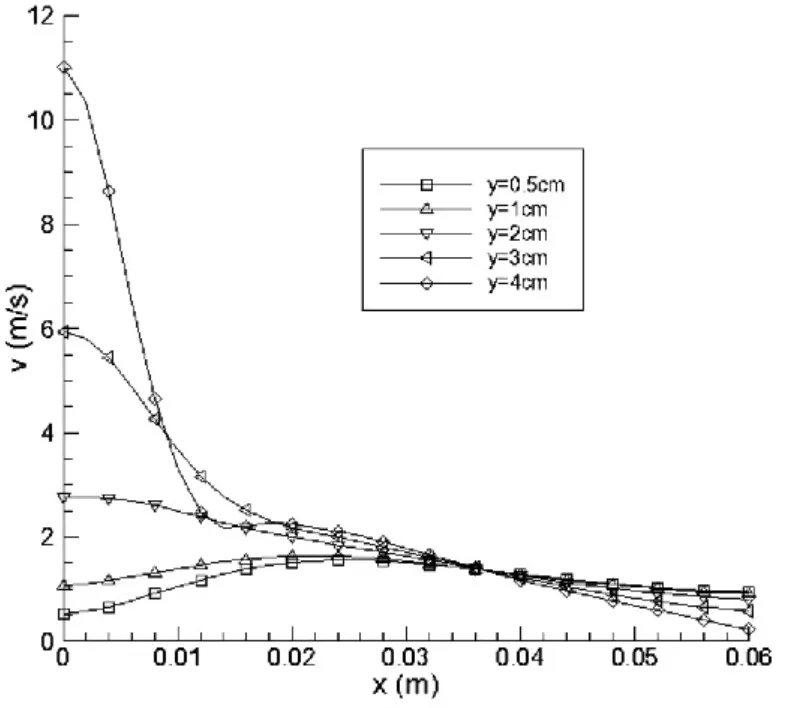
图10 泡沫金属层高h=4cm时,y=0.5cm、y=1cm、y=2cm、y=3cm、y=4cm等值线处的速度分布
图11显示,泡沫金属层高h=4cm时,y=0.5cm、y=1cm、y=2cm、y=3cm、y=4cm等值线处的温度分布。y=0.5cm所对应的温度最大,y=4cm所对应的温度最低,在每条等值线上,沿流线方向温度逐渐增加,y=3cm、y=4cm等值线上相同位置上的温度相差很小,且y=4cm所对应的温度分布出现突变的现象。这是由于温度分布和速度分布呈负相关的关系,并由于气旋的存在使y=4cm等值线上的温度分布出现突变的现象。

图11 泡沫金属层高h=4cm时,y=0.5cm、y=1cm、y=2cm、y=3cm、y=4cm等值线处的温度分布
3.8 泡沫金属层高对换热面摩擦系数的影响

图12 泡沫金属层高对换热面摩擦系数的影响
图12显示,泡沫金属层高对换热面摩擦系数的影响。h/H=0.25时,Cf沿 流线方向先增大,然后再减小,出现峰值,其整体值都比其他两种情况大;h/H=0.75时,Cf沿 流线方向逐渐增加,呈一条平滑的曲线。这是由于,泡沫金属高度越小,在喷嘴处形成的气旋半径越大,对换热面速度的影响越大,而泡沫金属高度越大,气旋半径越小,从而就对换热面的速度影响就很小,故而Cf较为平滑。
3.9 泡沫金属内等温线分布
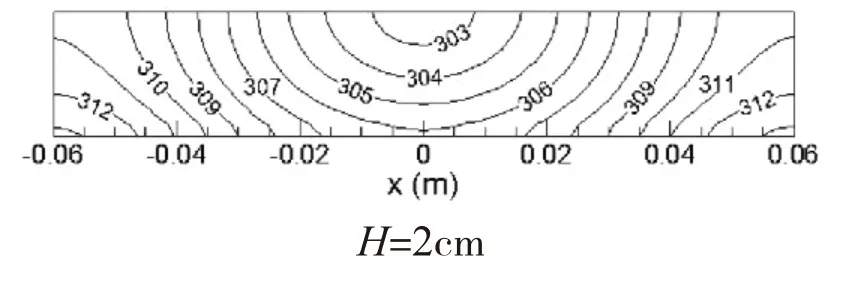
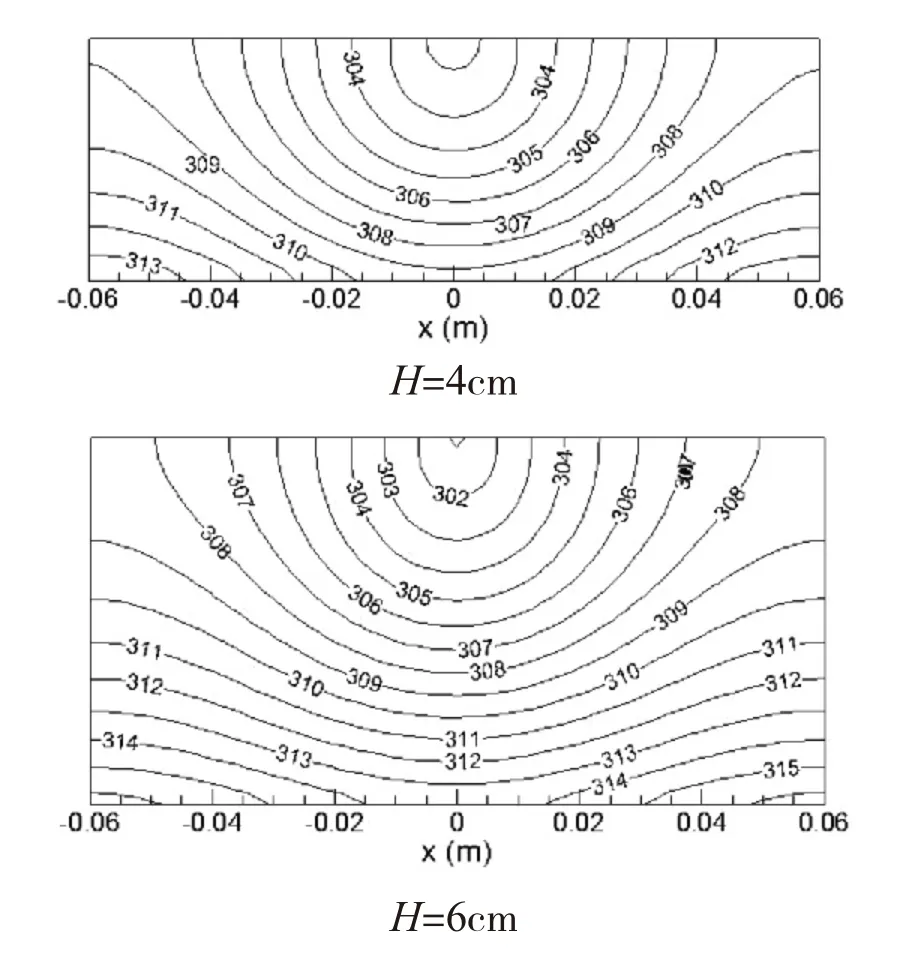
图13 泡沫金属内等温线分布
图13显示,泡沫层高不同(h=2cm, 4cm,6cm),其内的等温线分布图。泡沫金属层高h=2cm时,泡沫金属入口温度约303K,换热面上止滞点(x=0cm)处的温度约为306K,且入口等温线半径较大;泡沫金属高度h=6cm时,泡沫金属入口温度约301K,换热面上止滞点(x=0cm)处的温度约为313.5K,且入口等温线半径较小,接近换热面的等温线比较平滑;这就说明泡沫金属高度越大,越影响换热。这是由于泡沫金属层的厚度影响了气流在期内的流动,高度越大,其流动阻力越大。
4 结论
本文基于CFD技术分析冲击泡沫金属强化换热的机理和换热效果。通过分析泡沫金属的高度h,孔隙率ε,材质等变量对换热面的换热系数,Nu数,摩擦系数(Cf) 的影响,以及不同等值线的速度分布和温度分布,流道内的流线分布,泡沫金属的温度分布等场量的分布。得出以下结论:泡沫金属高度越小换热系数越大,摩擦系数越大,孔隙率越小Nu数越大,在泡沫金属材质为Cu时,Nu数最大,在止滞点(x=0cm)处换热效果最好,气流在泡沫金属内的流动阻力与泡沫金属的高度呈正相关的关系,气流在泡沫金属内流速分布和温度分布呈负相关的关系。当泡沫金属高度h=2cm,孔隙率ε=0.9,泡沫金属材质为铜时,冲击泡沫金属会在热源表面产生最优的换热效果。
