基于等效静态载荷法的连杆动态优化

李 伟，王 强，张艳岗，郝 贤

(中北大学能源动力工程学院，山西 太原 030051)

连杆作为柴油机的主要传力部件之一，在工作状态下承受着压缩、拉伸和弯曲等交变载荷，其主要失效形式是拉压疲劳破坏和失稳。为此，连杆应设计得足够粗壮，但这会使惯性载荷过大，影响柴油机的平衡性和稳定性。为使柴油机连杆既能承受各种拉压载荷的作用，又能使连杆的质量保持在最佳状态，需要对连杆进行优化设计[1]。众多学者对柴油机连杆进行了轻量化研究。刘晓洁[2]提出了基于Kriging元模型的柴油机连杆结构优化设计方法，采用拉丁超立方法采样并建立Kriging代理模型，再对其进行了准确性验证，在此基础上应用SQP求解器，进行连杆轻量化研究；张之涛等[3]对某柴油机连杆的预紧工况、受拉工况和受压工况进行了有限元分析，以连杆小头与杆身的过渡圆角和靠近连杆小头横截面内的倒角为设计变量，对连杆质量和最大等效应力进行优化设计；杨志波等[4]对连杆进行了有限元静态分析，以连杆的总质量为目标函数、应力为约束条件，采用步长搜索法优化了连杆的结构，降低了连杆的质量；秦健健等[5]通过分析连杆在最大受压工况下的应力和位移，结合Isight构建多岛遗传算法对连杆进行优化； Chandan等[6]对连杆不同部位的受力情况进行了分析和研究，从现有的设计参数开始，在最小应力条件下对连杆的小端和大端圆角半径进行最优选择；石舟等[7]对最大受压工况下的36MnVS4连杆进行了轻量化研究。上述对连杆的优化多采用有限元静态分析优化的方法，但由于静态分析并不能非常准确地模拟连杆的实际工作状态，因此基于静态分析的连杆结构优化设计有一定的局限性。

针对上述问题，本文使用等效静态载荷法[8]对连杆进行等效静态载荷作用下的动态优化设计。先通过面载荷等效数学模型求出等效静态载荷，再使用等效静态载荷进行连杆的分析及优化，实现对连杆的轻量化设计，为机械结构的动态优化提供思路。

1 结构等效静态载荷计算理论

1.1 等效静态载荷原理

当结构承受动态载荷时，在某一时刻结构会发生变形，从而产生一个位移场，如果在这一时刻存在一个静态载荷作用到结构上，产生与动态载荷作用下相同的位移场，那么称该静态载荷为这一动态载荷在某一时刻的等效静态载荷[9]。图1给出了静态载荷的等效过程。

由图1可以看出，动力学分析中计算时间步为(n+1)步，在等效时，把每个时间步看成一个静态工况，并且要求第si个等效静态载荷的系统响应与对应时间步的动态响应相同[10]。

图1 静态载荷等效过程

1.2 基于位移响应的等效静态转化

结构在动态载荷作用下的微分方程为：

MD(b)zD(t)+CD(b)zD(t)+KD(b)zD(t)=f(t)

(1)

式中：MD为动态质量矩阵，是设计变量向量b的函数；CD为动态阻尼矩阵；KD为动态刚度矩阵，是设计变量b和节点位移向量zD的函数；f(t)为t时刻的外载荷向量。基于位移响应计算的等效静态载荷可表示为：

feq=KLzD(t)

(2)

式中：KL为线性静态刚度矩阵；feq为t时刻的等效静态载荷。

由式(2)可求得与时间t一一对应的(n+1)个等效静态载荷，该等效静态载荷等于线性刚度矩阵KL与节点位移向量zD的乘积M。

1.3 基于等效静态载荷法的结构动态优化设计流程

由基于位移的等效静态载荷公式(2)可以看出，只有对结构进行瞬态分析之后才能计算得到其等效静态载荷。说明通过等效静态载荷计算的是已知的位移场。从这个角度来说，等效静态载荷是没有任何意义的，但是等效静态载荷最终要运用到结构优化中去，为后续优化设计奠定基础[11]。优化设计的具体步骤如图2所示。

2 连杆动态分析

2.1 连杆参数化模型

为方便后续优化流程，本文运用Creo对某柴油机连杆进行参数化建模，所建模型如图3所示。

图2 等效静态载荷优化流程

图3 连杆参数模型

图中连杆优化设计参数符号及含义、初始值见表1。

表1 连杆优化设计变量

2.2 连杆动态分析

连杆材料选取40Cr，其材料属性见表2。

表2 连杆材料属性

在施加连杆载荷时，先用连杆的气体压力曲线和惯性力曲线合成连杆的受力曲线，如图4所示。对连杆受力曲线时间点进行离散处理，将其离散为17个载荷步来模拟连杆工作过程中的受力，连杆的受力施加在活塞销的外表面，约束条件设置为连杆大头端面全约束。对活塞销与连杆衬套和连杆衬套与连杆小头之间添加含摩擦的标准接触。Workbench中时间步定义方式选择为子步，步数设置为10，即17个载荷步中每一个载荷步之间等分为10份进行计算。为进一步提高最终的计算精度，在连杆关键位置处，即最大受力载荷区间9,10,11载荷步区间适当增大时间子步至30。

图4 连杆受力曲线

通过分析得出在第140步，即时间为0.034 2 s时连杆的位移以及应力最大，位移云图如图5所示，应力云图如图6所示。

图5 动态载荷作用下连杆位移云图

图6 动态载荷作用下连杆应力云图

从图5和图6可以看出，连杆的最大应力主要集中在杆身，为237.81 MPa，小于连杆材料许用应力，最大位移主要集中在连杆小头部分，为0.175 66 mm，在连杆材料的弹性变形范围内。

3 等效静态载荷转化及优化

3.1 等效静态载荷计算

在一般的动态优化中，均存在计算量大且极易造成结果不收敛的情况，在这种情况下，基于位移等效静态载荷法为结构动态优化设计提供了有效途径。优化数学模型如下：

(3)

文中提取瞬态分析中应力最大时刻的节点位移作为等效静态载荷作用下的位移和动态载荷作用下的位移，由于连杆为对称结构，故选取如图7所示的8个区域节点来表征整个连杆的状态，目标设置为等效静态位移与提取的瞬态位移方差和最小，设计变量设置为作用在活塞销上的载荷P。

图7 等效关键位置点示意图

为节省等效静态载荷计算时间，提高计算的收敛速度，采用序列二次规划法进行连杆的等效静态载荷计算，得到静态载荷值Ps=23.782 MPa。

为便于等效静态载荷位移和动态载荷位移的对比分析，将各个关键位置的位移误差绘制成直方图，如图8所示。

同理，绘制最大等效应力对比分析直方图，如图9所示。

由图8和9可以看出：通过等效静态转化数学模型以及在Isight中实现等效静态转化，等效后的位移和动态载荷作用下的位移误差在4.2%以内。将等效静态载荷加载到连杆上进行分析，通过对比分析关键位置点的应力变化，发现最大误差也在4%左右，进一步验证了等效静态载荷数学模型以及等效方法的准确性。

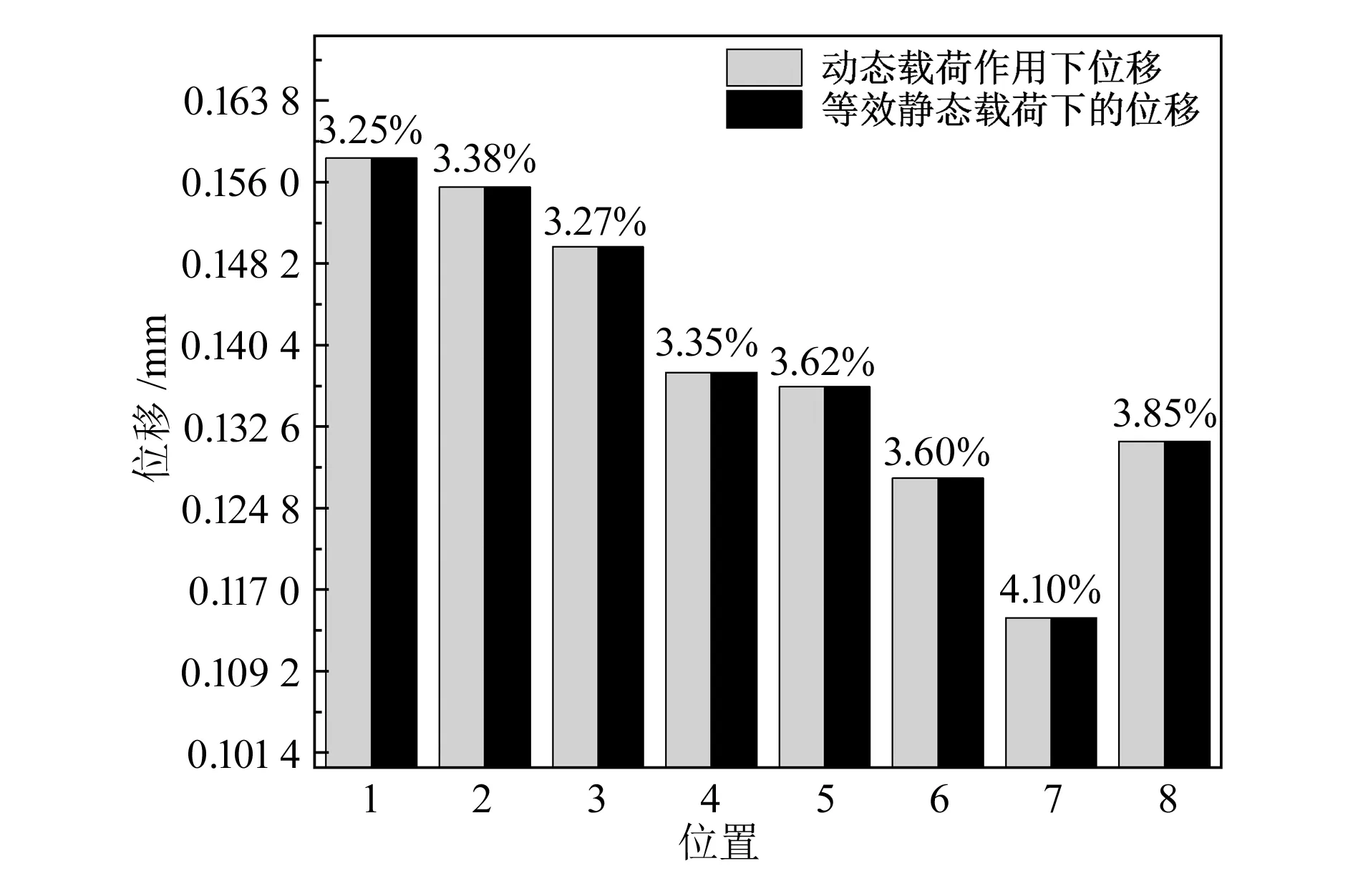
图8 关键区域位置位移误差对比示意图

图9 关键区域位置应力误差对比示意图

3.2 等效静态载荷作用下连杆优化设计

基于位移等效得到的等效静态载荷与动态分析得到的最大载荷相差不大，看似等效分析的意义不大，但是等效静态载荷考虑了结构质量和惯量的变化对系统动态行为以及部件载荷条件的影响，更加符合机械结构在实际工况下的作用情况，且使用等效载荷是基于优化而提出的方法，最终的目的是运用到机械结构优化中，这对于机械结构在动态载荷作用下的优化具有重大的意义。

以连杆结构参数作为设计变量、以连杆质量最轻为目标函数、以等效静态载荷作用下连杆结构的最大等效应力σmax不超过材料许用极限应力[σ]为约束条件进行连杆的优化设计。优化数学模型如下：

minMass

s.t.σmax≤[σ]

32.9≤DS_1≤39.6

9≤DS_2≤11

90≤DS_3≤110

108≤DS_4≤132

54≤DS_5≤66

(4)

优化类型选择基于Kriging模型的响应面优化，优化算法选择MOGA，候选点数量改为1，优化结果见表3。

表3 连杆优化结果

从等效静态载荷作用下的优化结果可以看出，优化后连杆质量减轻了6.70%，并且最大等效应力明显降低，优化效果显著。这不仅对连杆轻量化研究具有重大意义，还为其他机械结构的动态优化设计提供了可行性参考。

4 结束语

本文采用等效静态载荷法对连杆进行等效静态载荷作用下的动态优化设计，相比于传统的极限工况静态优化，基于等效静态载荷法的连杆动态优化设计充分考虑了结构质量和惯量的变化对系统动态行为以及部件载荷条件的影响，更加符合机械结构在实际工况下的作用情况，这对于机械结构在动态载荷作用下的优化具有重大意义。

通过对某柴油机连杆的优化设计，结果表明连杆质量减少6.70%，最大等效应力明显降低，实现了连杆轻量化设计，进一步验证了等效静态载荷法的正确性，对其他工程实际应用问题具有一定的指导意义。