砂岩蠕变特性试验及三维非线性力学模型研究

刘凡熙，赵立财，余建星，蒋腾健

(1. 广西南宁水利电力设计院，广西 南宁 530001；2. 天津大学 水利工程仿真与安全国家重点实验室，天津 300354；3. 南宁市城市建设投资发展有限责任公司，广西 南宁 530031)

岩石是一种非均质非线性的地质材料，不仅具有弹性和塑性特征，其蠕变特征也是岩石力学中的核心研究内容之一[1]。水利水电工程、采矿工程、隧道工程中岩体蠕变变形明显会对工程建设与运营造成威胁[2]。

对于岩石蠕变特性已有大量研究，江宗斌[3]探究水化学溶液和低温对板岩蠕变特性的影响规律，基于此建立水化学-应力-损伤耦合模型；徐鹏等[4]以粉砂岩为研究对象，开展多级增量循环加卸载流变试验，根据试验结果提出一种可描述塑性应变变化规律的裂隙塑性元件，与Burgers模型串联从而得到一个新的蠕变模型；梁冰等[5]进行片麻岩三轴压缩蠕变试验，对其起始蠕变应力阈值、长期强度和加速蠕变启动时间进行分析；何峰等[6]开展不同含水率下的煤岩蠕变试验，研究水对煤岩蠕变变形、长期强度等的影响。

目前关于砂岩蠕变特性试验所建本构模型多为一维应力状态下的力学模型，难以反映岩石在三维应力状态下的蠕变行为。本文以某大型水利枢纽工程坝肩砂岩为研究对象，进行差异性围压条件下的三轴压缩蠕变试验。重新定义了一个与时间和围压都相关的黏弹性模量E(p，t)，并得到了新的三维非线性力学模型。

1 蠕变试验

1.1 试验设备

蠕变试验采用RLW-2000型岩石三轴流变试验系统。该试验仪器由轴向、围压、孔压加载系统进行荷载控制，由伺服、控制系统进行荷载和位移控制，通过数据采集和自动绘图系统进行试验成果采集和输出。轴向加载系统和围压加载系统的控制部分采用全数字伺服控制器，设备最大加载围压70 MPa，最大轴向荷载2000 kN。

1.2 试验材料及方案设计

本文研究背景为某大型水利枢纽工程坝肩边坡，在滑带附近取砂岩样，将岩样加工成直径50 mm、高100 mm的圆柱样，并打磨断面使其平整。砂岩基本物理力学参数如表1所示。

表1 岩石基本物理力学参数Table 1 Basic mechanical parameters of rock

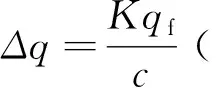
图1 不同加载等级下的偏应力设置图Fig.1 Schematic diagram of deflection stress at different loading levels

1.3 试验结果

图2为分级加载蠕变曲线，将每级轴向荷载(偏应力)标示在曲线上方。在图2的基础上利用玻尔兹曼线性叠加原理[7]可得到分别加载蠕变曲线，如图3所示。

图2 分级加载蠕变曲线Fig.2 Graded loading creep curves

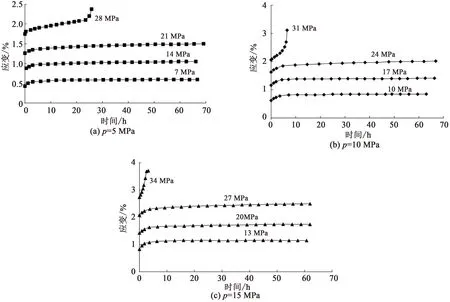
图3 分别加载蠕变曲线Fig.3 Separate loading creep curves

根据图2、3可作如下分析：

(1)岩石在轴向荷载下，首先产生一定量的瞬时弹性应变，之后蠕应变发展累积，蠕应变量值远小于弹性应变量值。当偏应力水平达到最后一级时，岩石出现加速蠕变阶段，蠕变速率急剧增长，在短时间内屈服破坏。由此可知，岩石不仅表现有瞬时弹性阶段、衰减和稳定蠕变阶段，达到破坏偏应力水平后还表现有加速蠕变阶段。

(2)在围压5 MPa～15 MPa下，岩石蠕变试验历时分别为228 h、203 h和188 h，破坏偏应力水平持续时间分别为25.81 h、6.49 h和3.24 h，蠕变试验总历时和破坏偏应力水平持续时间随着围压的增大而递减。

2 试验结果

2.1 蠕变速率

研究岩石蠕变速率的变化规律，可以更好地认识蠕变变形发展过程。张春阳等[8]提出如下蠕变速率解析方法：

(1)

式中：Δti为蠕变时间;ε1，ε2，…，εn为各微段蠕变；Δε1，Δε2，…，Δεn为微段蠕变之差；Δε和vi表示Δti时间内总应变和平均应变速率。

根据式(1)的方法绘制蠕变速率曲线，如图4所示，限于篇幅，仅给出围压5 MPa下的蠕变速率曲线。

图4 蠕变速率曲线Fig.4 Creep-rate curves

由图4可看出，岩石第4级蠕变加载曲线呈“桶”形，曲线簇从左到右分为3个区域：衰减蠕变阶段、稳定蠕变阶段和加速蠕变阶段。其中岩石第1～4级加载等级下的衰减蠕变阶段，对应图中区域Ⅰ，该阶段的蠕变速率在同一加载等级下逐渐递减，在同一时刻随着加载等级的提高而递增；稳定蠕变阶段对应图中区域Ⅱ，该阶段的蠕变速率在同一加载等级下基本保持恒定，在同一时刻随着加载等级的提高而递增;加速蠕变阶段对应图中区域Ⅲ，蠕变速率剧增，短时间内达到极限值。

2.2 稳态蠕变速率与偏应力的关系

绘制不同围压不同加载等级下的岩石稳态蠕变速率与偏应力的关系曲线，如图5所示。

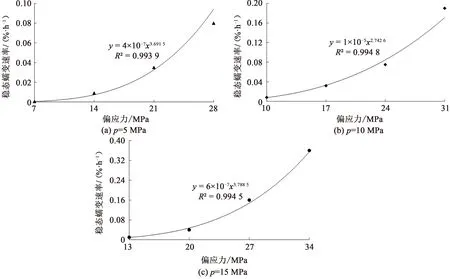
图5 稳态蠕变速率与应力水平关系曲线Fig.5 Curves of the relationship between steady creep rate and stress level

由图5可知，3种围压下的稳态蠕变速率与偏应力皆呈幂函数关系，R2分别为0.993 9、0.994 8和0.994 5。在岩石的稳定蠕变阶段，虽然稳态蠕变速率与围压呈幂函数增长关系，但稳态蠕变速率变化范围较小，相对比较恒定，由此说明该阶段是岩石微裂纹不断发育和扩展的过程，岩石蠕变全过程皆处于微裂纹发育、延展直至贯通的活动状态。

2.3 等时应力-应变关系

选取图3中1 、11、21、31、41、51、61 h共7个时间节点的偏应力-应变数据，绘制成等时蠕变曲线簇，如图6所示。李良权等[9]取该曲线簇的拐点为岩石长期强度。

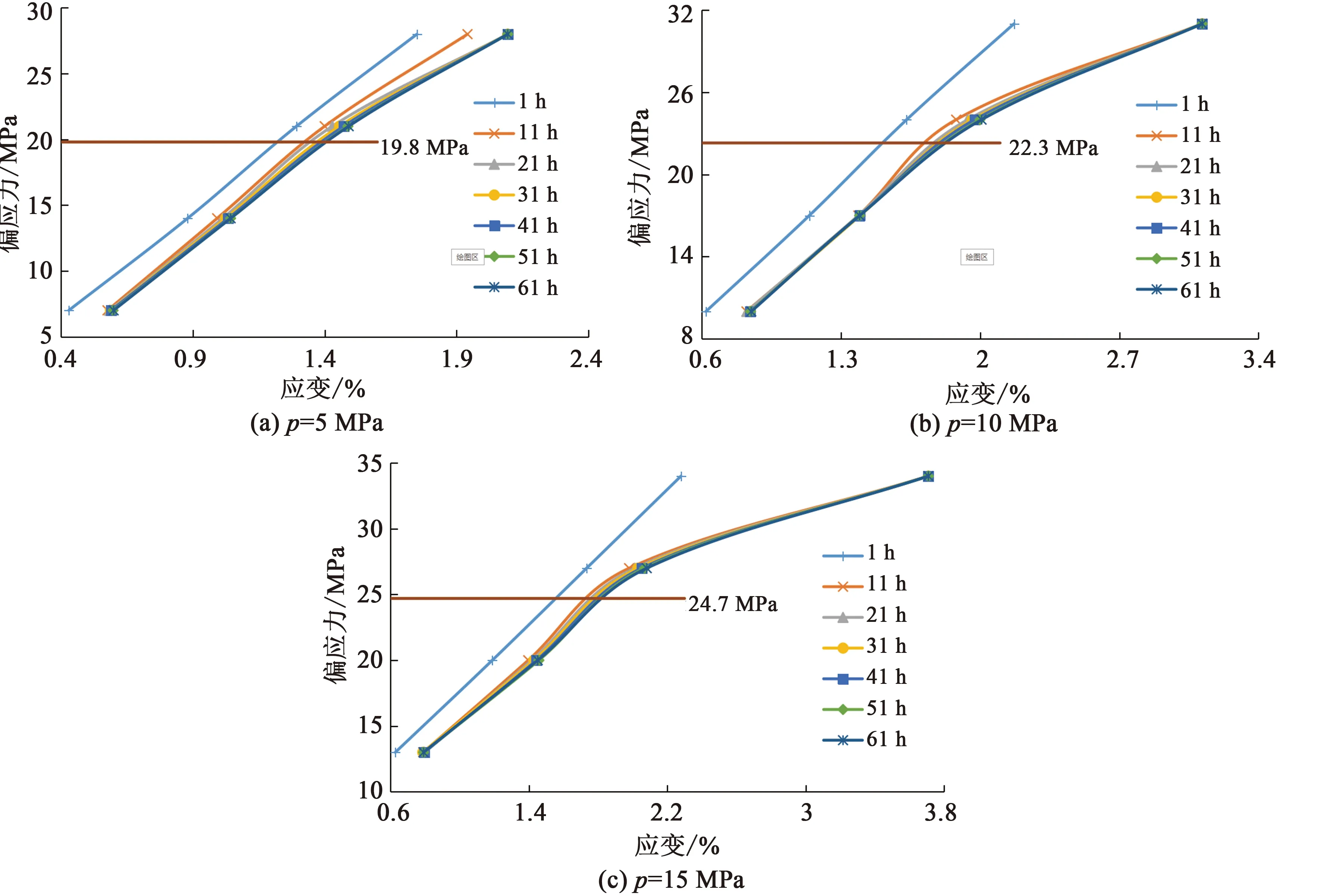
图6 等时蠕变曲线簇Fig.6 Isometric creep-curve clusters

由图6可知，通过取拐点的方法，围压5 MPa、10 MPa和15 MPa下的长期强度分别为19.8 MPa、22.3 MPa和24.7 MPa，长期强度随围压的增强而逐渐增大。随着时间增长，等时蠕变曲线簇逐渐偏于横轴，表现出明显的非线性特征。当岩石未进入加速蠕变阶段时，蠕变变形为黏弹性变形，对应图6中曲线簇的近线性段，于是将等时应力-应变曲线的斜率定义为黏弹性模量E(p)。图7为黏弹性模量与不同围压的关系曲线。

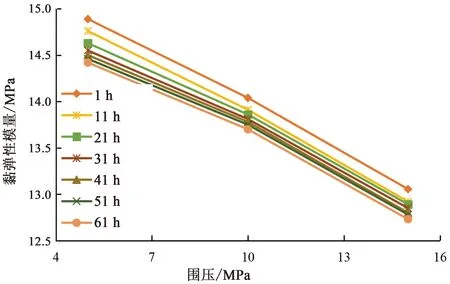
图7 黏弹性模量与围压关系曲线Fig.7 Relationship between viscoelastic modulus and confining pressure

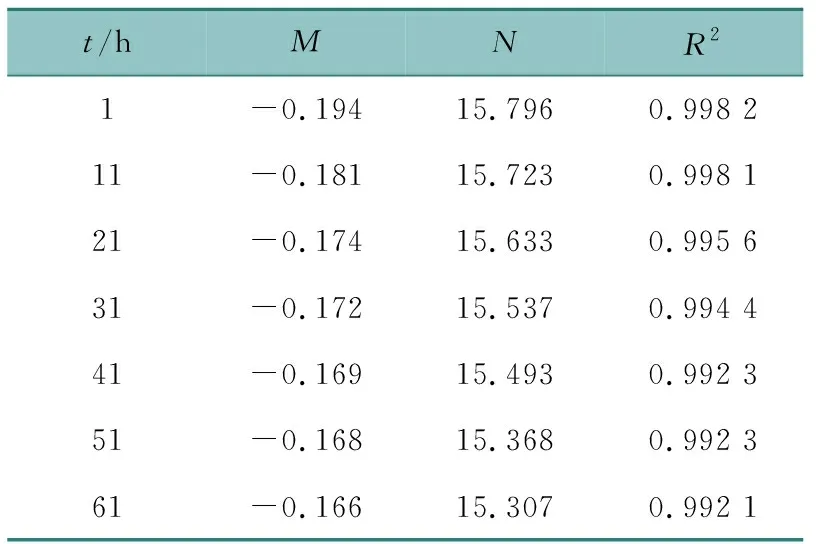
由图7可发现曲线近线性，用式(2)对图7中7条曲线进行线性回归，结果如表2所示。

E(p)=Mp+N。 (2)

由表2可知，R2平均值为0.994 7，E(p)的两个参数M、N的变化在某种意义上可反映砂岩蠕变的非线性特征，图8为M、N随时间变化的数据分布。

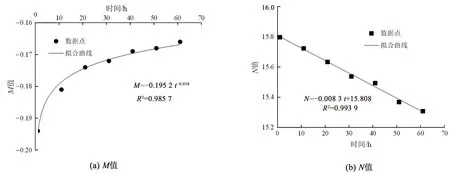
图8 M和N拟合Fig.8 Fitting of M and N

从图8可看出，M值与时间t呈幂函数关系，N值与时间t线性相关。式(3)、(4)分别为M、N的拟合结果：

M=-at-b,

(3)

N=-ct+d。

(4)

将式(3)、(4)代入式(2)得

E(p,t)=-at-bp-ct+d。

(5)

式(5)即为本文所建可反映差异性围压条件的黏弹性模量，通过式(5)可建立砂岩受时间和围压影响的时效力学响应过程。

3 三维蠕变力学模型

3.1 模型建立

元件模型具有结构简单、便于应用的特点，但常用的传统元件模型如西原模型、Burgers模型等，其本构方程为线性状态，难以描述岩石蠕变的非线性特征。故本文在传统Burgers模型的基础上，串联一个非线性黏塑性元件[10]，从而得到六元件模型。假定其中Kelvin体中的弹性体服从式(5)，从而得到一个新的非线性蠕变力学模型。模型示意图如图9所示。

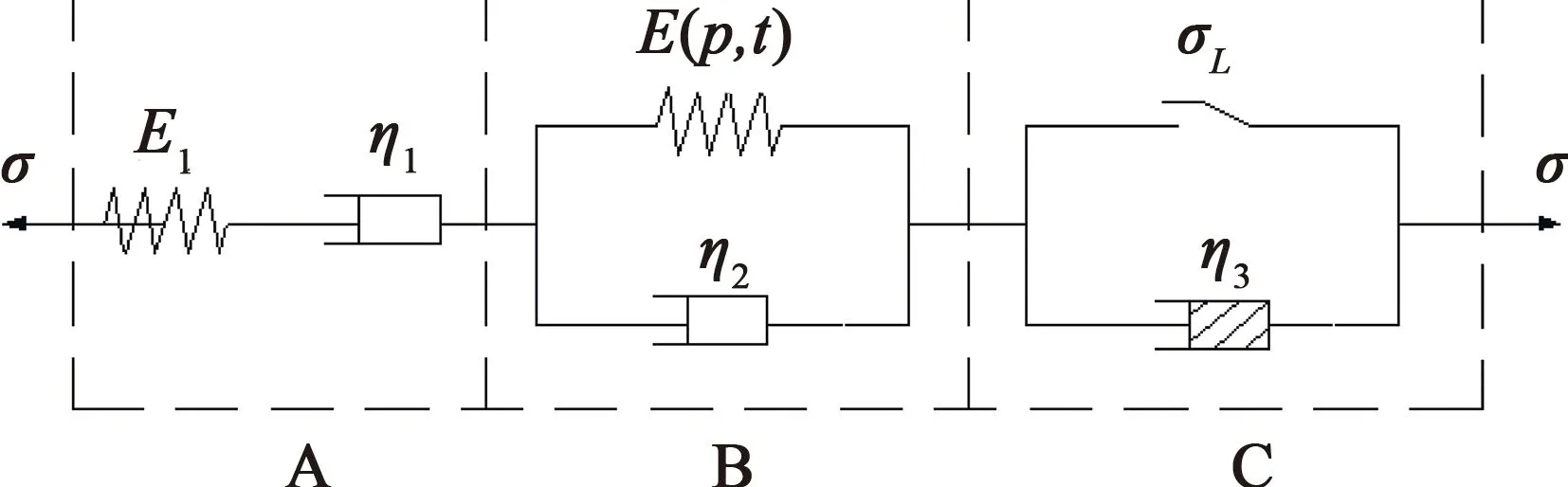
图9 模型示意图Fig.9 Illustration of the model

当σ0<σL时，非线性黏塑性体失效，其状态方程为：

(6)

式中，σ0为初始应力，σA、εA、E1和η1分别为图10模型A部分的应力、应变、弹性模量和黏滞系数，σB、εB、E(p,t)和η2分别为模型B部分的应力、应变、黏弹性模量和黏滞系数。相应的蠕变方程为：

多年来，何王庙故道一直是周边40万人口、200多户渔民、80万亩农田的水源地。为给江豚提供一个舒适的生存环境，监利县对保护区水域的渔业捕捞、网箱养殖、洲滩放牧和农业污水排放等方面进行了综合治理，并赎买了核心区渔民的捕捞工具，杜绝核心区捕捞活动。

(7)

当σ0≥σL时，非线性黏塑性体发挥作用，相应的状态方程为：

(8)

式中，σC、εC和η3分别为模型C部分的应力、应变和黏滞系数，σL为长期强度。相应的蠕变方程为：

(9)

式(7)、(9)即为本文所建非线性蠕变力学一维模型。

假设岩石为各向同性体，根据广义Hooke定律，三维应力状态下的本构关系为

(10)

式中，σm为球应力张量，Sij为偏应力张量，K为体积模量，G为剪切模量。

由于在岩体工程中，岩石多处于三维应力状态，而本文岩石蠕变试验也是三轴压缩应力路径，故而有必要建立三维力学模型。假设岩石为各向同性体，分解岩石内部的应力张量，于是有

σij=Sij+δijσm，

(11)

一般认为，σm只改变物体体积，Sij只引起形状变化，因此也可以将应变张量分解为

εij=eij+δijεm，

(12)

式中，εij为应变张量，εm为球应变张量，eij为偏应变张量。

为了简化问题，假定岩石材料蠕变仅由偏应力张量引起，与体积变化无关，将式(7)、(9)推广为三维情形

(13)

式中，(Sij)0为初始偏应力张量，(Sij)L为对应长期强度的偏应力张量。

在本文三轴压缩蠕变试验中，中间主应力σ2=p，于是

σm=(σ1+2p)/3，

(14)

再结合式(11)，则有

S11=2(σ1-p)/3，

(15)

将式(5)、(15)代入式(13)可得

(16)

式(16)即为本文所建的新的三维非线性蠕变力学模型的轴向蠕变方程。

3.2 模型参数识别及验证

新建三维蠕变模型中有G1、η1、η2、η3、a、b、c、d、(σ1-p)L等共9个参数。图7取拐点的方法可确定岩石长期强度σL，由于σL是通过等时偏应力-应变关系求解而得，所以偏应力(σ1-p)L在数值上等于σL，通过广义Hooke定律可求解G1。另外7个参数通过数学软件1stOpt，基于爬山算法(Hill Climbing)求解。图10为识别结果与图3试验数据对比曲线，表3为模型参数。

图10 试验数据与预测结果对比曲线Fig.10 Comparison curves between test data and predicted results

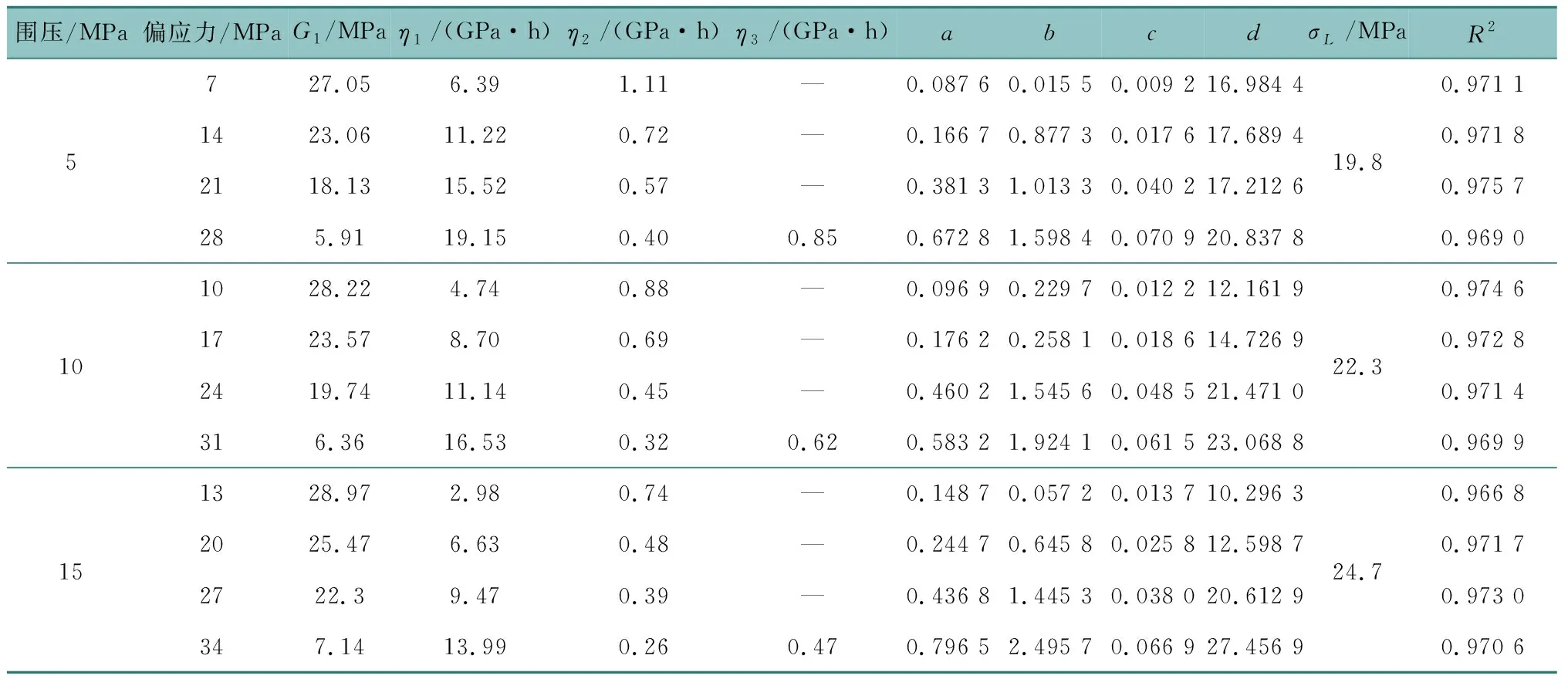
表3 蠕变力学模型参数

由图10和表3可看出，本文新建三维非线性蠕变力学模型具有良好的识别效果，R2平均值为0.971 5，能较为准确地描述砂岩在三维应力状态下的蠕变力学行为。砂岩在不同应力状态下，加速蠕变阶段具有不同的曲线特征，新建三维模型仍具有较强的识别能力，由此证明本文所建模型的合理性和适用性。

4 结论

(1)岩石稳态蠕变速率与围压呈幂函数增长关系，稳定蠕变阶段是岩石微裂纹不断发育和扩展的过程，岩石蠕变全过程皆处于微裂纹发育、延展直至贯通的活动状态。

(2)通过等时蠕变曲线簇取拐点，得到砂岩在围压5 MPa、10 MPa和15 MPa下的长期强度分别为19.8 MPa、22.3 MPa和24.7 MPa，长期强度与围压大小呈正相关。砂岩的长期强度折减较大，实际工程应用中应考虑其折减问题。

(3)本文通过研究砂岩蠕变的非线性特征，定义了与围压相关的黏弹性模量E(p)，经过推导变换得到了可反映岩石蠕变受时间和围压影响的E(p，t)。在传统Burgers模型的基础上，串联一个非线性黏塑性元件，并将E(p，t)应用到模型中，得到一个新的一维蠕变力学模型。将其拓展到三维应力状态，进行模型辨识，证明新建三维非线性蠕变力学模型描述砂岩在不同三维应力状态的可行性和合理性。