基于因果分析和相似日选择的共享单车需求量预测组合模型

徐长兴，汪伟平*，昌锡铭，包旭，吴建军

(1.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；2.淮阴工学院 交通工程学院，江苏 淮安 223000)

无桩式共享单车是在共享经济和物联网等技术浪潮下产生的一种新的慢行交通模式，是城市公共自行车系统的重要组成部分[1]。共享单车取消了传统公共自行车固定的停车桩，解决了因停车桩数量少而造成的“还车难”等问题。共享单车的出现在有效解决城市居民出行“最后一公里”问题的同时，也对减少大气污染和缓解城市交通拥堵等起到了积极作用。

虽然目前无桩式共享单车呈现出良好的发展态势，但是在特定时间段的某些区域仍存在借还车次不平衡、车辆投放数量不合理、车辆调度不及时等问题。人们出行特征的时空非均衡性，特别是早晚高峰客流的潮汐现象导致了共享单车系统在时空上分布的不均衡[2]。区域内单车需求大于供给，会导致无车可借，产生“借车难”等问题，反之会导致大量单车无人使用而长时间闲置，占用公共空间。

高效及时的单车调度是单车系统时空分布再平衡的重要途径，而准确的短时出行需求预测是单车科学调度的基础。若采取人工巡查的方式或者监测平台利用GPS定位监控到不平衡之后再派卡车执行单车的调配，缺乏对未来需求量的预判，会造成严重的滞后和效率低下[3]。因此，准确地预测区域内各时段的需求量是进行车辆调度和共享单车系统布局优化的基础，也是提高企业服务质量和用户体验的关键环节。

从预测模型发展角度，共享单车的需求预测方法可以分为传统的统计学和机器学习两大类。统计学方法如差分整合移动平均自回归模型(autoregressive integrated moving average model，ARIMA)、多元回归分析、马尔可夫链[4]等传统统计推断模型，是最早被应用到共享单车需求预测的一类方法。Kaltenbrunner等[5]基于巴塞罗那社区自行车项目某站点的数据，运用ARIMA模型，对可用自行车的数量进行了预测。闫厦[6]根据单车需求量的时序性，建立了考虑季节周期的ARIMA模型，该模型可以刻画出行需求的周期性和趋势性。尽管ARIMA等统计推断模型在时间序列建模中显示出一定的有效性，但是无法刻画需求量与各影响因素之间的时空依赖性等复杂非线性关系。而且，实际应用中数据的噪声会降低参数估计的可靠性，因而预测效果不是特别理想。近年来，随着海量出行数据的积累和计算能力的提高，利用机器学习方法发现交通系统的动态特性逐渐成为一个研究热点。支持向量回归(support vector regression, SVR)、随机森林(random forest, RF)和神经网络(neural networks, NN)的模型已广泛用于共享单车的短时需求预测。根据无桩式共享单车需求量的时间序列特征，孔静[3]建立了基于BP神经网络的预测方法模型，由于缺乏对天气、位置等外部影响因素的建模，预测效果并不理想。机器学习算法能够综合考虑出行需求的时间序列特征和外部影响因素。研究表明影响单车需求量的外部因素主要包括天气因素(温度、降水量、风速等)[7]和位置因素[8]，此外还受到人口统计特征、建筑环境特征[9]和交通事件等[10]因素的影响。种颖珊等[11]基于2015年美国湾区70号站点的自行车需求量数据，研究了时间因子、气象因子以及关联站点对需求量的影响，建立了基于随机森林与时空聚类的模型，实现了对有桩自行车需求量的预测。Li等[12]提出了一种分层预测模型，运用二分聚类算法和渐变增强回归树模型来预测站点的借还车数量。

尽管机器学习算法可以有效地对共享单车短时出行需求的时间趋势进行识别和预测，但是很多机器学习算法都是黑箱模型，无法刻画需求量与影响因素之间的关系，从而使得预测结果的可解释性较低。在实际建模中，由于数据噪声、数据量小等原因，单个机器学习算法的预测性能往往不高，对于不同预测任务的泛化性能差[13]。集成学习通过构建并结合多个学习器来完成学习任务，可获得比单一学习器显著优越的泛化性能。Stacking策略是一种典型的集成学习方法[14]，将初级学习器的输出作为次级学习器的输入，从而实现融合多个学习器的预测结果。相较于对弱学习器的结果做平均或者投票等简单的逻辑处理，Stacking策略能够结合多个模型的优点，降低泛化误差，提升预测的准确性。作为刻画两变量之间因果关系的分析模型之一，格兰杰因果关系模型可以刻画共享单车的出行需求与天气指标之间的因果关系。灰色关联分析通过关联度指标，可以对共享单车系统中不同日期之间的相似程度进行量化分析。

因此，本文基于北京市共享单车用户的骑行数据和天气数据，将研究区域划分为若干网格单元，提出了一种基于Stacking策略的共享单车需求组合预测模型，构建了以神经网络、随机森林回归、支持向量回归等算法为基模型的不确定性集成模型。该框架通过将多个学习器进行结合，在无桩式共享单车分区域的短时需求量预测任务中可获得比单一学习器显著优越的准确性和泛化性能。本文的贡献在于：一是将格兰杰因果检验方法应用到筛选影响单车需求量的天气指标中，相较传统的仅仅依靠皮尔逊相关系数等相关性指标，更加合理；二是充分考虑了待预测日各时段与历史日的天气特征向量间的相似性，采用灰色关联度指标，筛选出具有高度相似性的相似日样本集，该方法可以对训练样本进行有效约简，减少了模型的训练时间；三是基于神经网络、随机森林回归、支持向量回归等算法建立组合预测模型，提高了单车需求量预测模型的预测精度和泛化性能。

1 数据来源和影响因子分析

1.1 数据来源

同一区域有多个品牌的共享单车，目前各个单车运营企业的车辆调度工作环节是相互独立的，因此需要针对各个品牌共享单车的需求量分别进行预测。考虑到市场份额、用户黏性等因素，本文选用北京市摩拜单车用户骑行数据进行研究，时间范围是2017年5月10日—31日。北京市是全国共享单车投放数量最多的城市之一，摩拜单车在共享单车投放总量中占比最大。因此选择北京市摩拜单车用户骑行数据来研究共享单车的需求预测问题，具有一定的典型性和代表性。通过对单车空间分布的初步研究，发现北京城郊区的单车密度较低，而四环内单车投放密度、出行需求较大，因此选取该区域作为研究对象。研究区域的具体位置为东经116.278°—116.499°，北纬39.836°—39.997°。主要的字段名称和描述统计见表1。

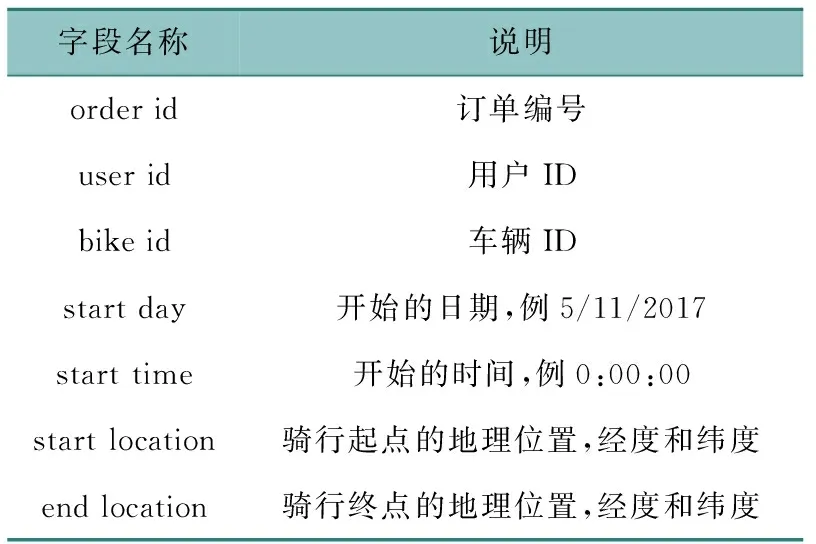
表1 字段描述

气象数据和空气质量数据主要从国家气象科学数据中心和相关天气网站(http://rp5.ru)(2017年5月10日—31日)收集得到。获得的数据包括地面2 m处的温度和相对湿度、气象站水平的大气压、地面高度10 m处的风速、水平能见度等。将下雨、雾霾、大风、晴天四类天气事件分别赋值为0、1、2、3。对于残缺的数据，采用线性插值法进行补全数据。表2汇总了所考虑变量的描述统计量。

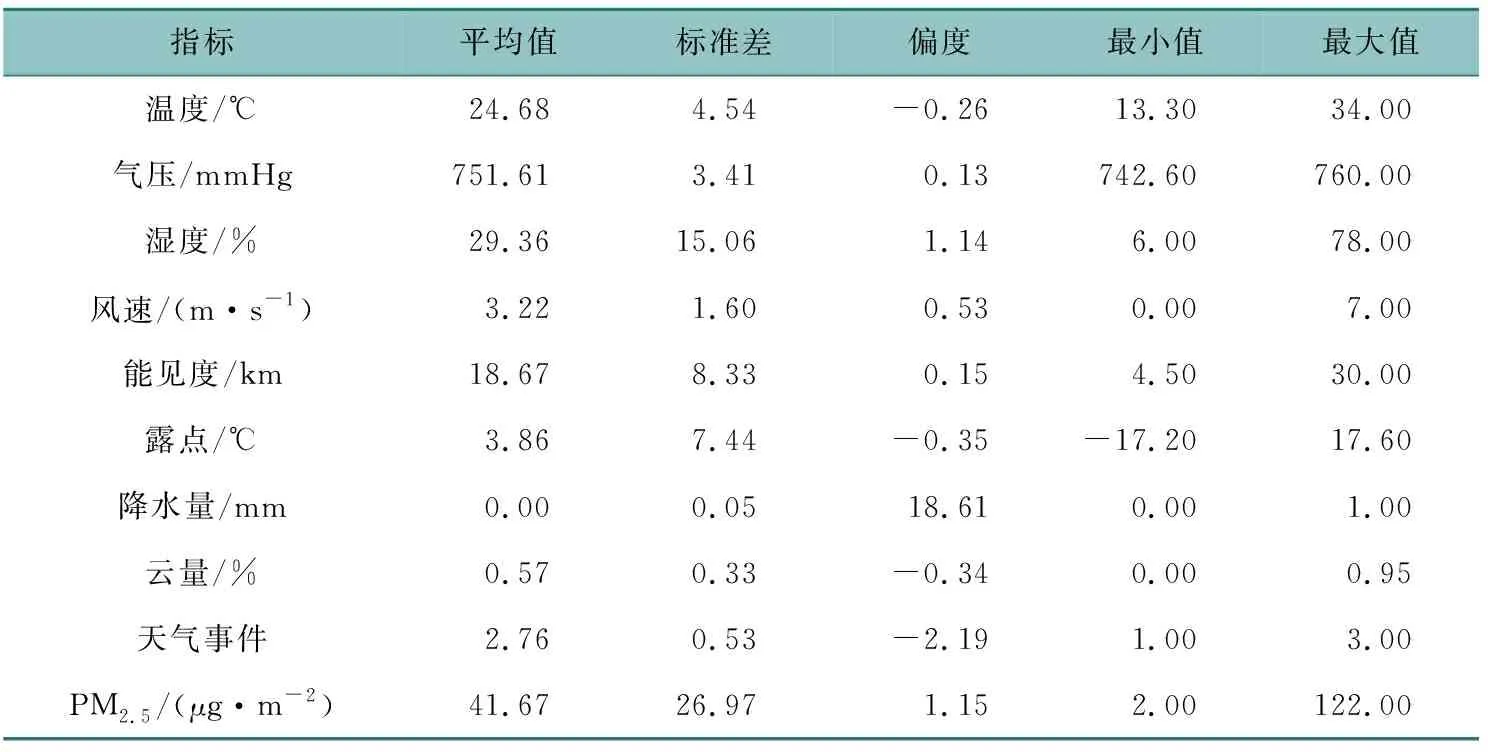
表2 天气指标的描述性统计分析

1.2 影响因素分析

1.2.1 时间因素的影响

1.2.2 天气因素的影响

共享单车相比于地铁、公交等更容易受到天气、空气质量等因素的影响。通过计算各天气指标与需求量的皮尔逊相关系数可知，需求量与温度、风速、能见度、露点、云量、天气事件、PM2.5的皮尔逊相关系数分别为0.38、0.21、0.07、0.03、0.09、0.11、0.07，均大于0，因此呈正相关关系；需求量与气压、湿度、降水量的皮尔逊相关系数分别为-0.22、-0.26、-0.04，因此呈负相关关系。通过对天气数据进行统计分析，发现不同日期的天气状况差异较大。本文采用的数据中包含了下雨、雾霾、大风、晴天等常见的天气状况，因此具有一定的代表性和典型性。

2 出行需求预测模型

2.1 基于因果检验的天气指标选择

天气因素是影响需求量的一个重要因素，然而刻画天气因素的指标有很多，如何科学地选取指标对提高预测模型的准确度至关重要。有学者从相关性的角度出发，借助皮尔逊相关系数等选取与出行需求相关性较大的天气指标。然而辛普森悖论的存在证明了相关性的不足，该悖论证明存在随机变量X和变量Y在边缘上正相关，但是给定另外一个变量Z后，在Z的每一个水平上，X和Y都具有负相关的可能性[15]。因此仅仅依靠皮尔逊相关系数等相关性指标去筛选天气指标显然是不合适的。如何从数据中发现其蕴藏的内在因果关系，是近年来数据科学研究领域的热点之一。因此，共享单车的出行需求与天气指标之间的因果关系及其背后的因果机制需要进一步挖掘。

格兰杰因果关系模型是由诺贝尔经济学奖得主格兰杰于1969年首次提出的一种刻画二变量之间因果关系的分析模型，是数据科学、金融分析、医学等领域挖掘数据间内在因果关系的重要工具。其基本思想是：若序列X有助于解释序列Y的未来变化趋势，即在序列Y关于自身历史信息的回归模型中，添加X的历史信息会显著地提升回归模型的解释能力，那么序列X是序列Y的格兰杰原因[16]。另外，为了避免非平稳序列带来的虚假因果，必须保证检验的序列是平稳的。

检验天气指标X是否为引起需求量Y变化的格兰杰原因的步骤如下。

首先，建立如下两个向量自回归模型：

(1)

(2)

式中：α0表示常数项；αi和βi是模型的系数；p和q分别为变量需求量Y和天气指标X的最大滞后期数，可以采用赤池信息准则(Akaike information criterion,AIC)进行确定；εt为白噪声。若天气指标X不是引起需求量Y变化的格兰杰原因，则自回归模型中系数βi应该为0，因此检验的原假设设定为H0:β1=β2=…=βq=0。采用的检验统计量分别为两个自回归模型，即公式(1)和(2)的残差平方和R1和R2构造的F统计量。

(3)

式中，R1、R2分别为公式(1)和公式(2)的残差平方和，n为样本容量。如果满足F>Fα(q,n-p-q-1)，表明天气指标X和需求量Y存在统计意义下的格兰杰因果关系，即天气指标X有助于预测需求量Y。

2.2 基于灰色关联分析的相似日确定

当前的需求量预测模型往往会选择与待预测日相邻的历史数据或者依据人工经验选取的相似日作为输入，具有一定的盲目性和不合理性。预测的效果往往不理想，尤其是待预测日的天气状况与前若干天差别较大时，需求量会发生明显的波动变化。因此，为了提高需求量的预测精度，合理有效地选取预测相似日非常重要[17]。

通过计算待预测时段与历史时段的灰色关联度指标，确定与待预测日各时段相似程度最高且日期属性(工作日或非工作日)相同的样本集数据。相似日的灰色关联度指标计算步骤如下。

首先选取温度、风速等m个通过格兰杰因果检验的天气因素构建因素矩阵，则第i时段样本的天气特征向量和待预测时段的天气特征向量可以表示为：

Xi=[xi1,xi2，…，xim]，i=1,2，…，N，

(4)

X0=[x01,x02，…，x0m]，

(5)

式中，N为历史同时段样本总数，xim为第i个样本的第m个天气因素值，x0m为待预测时段特征向量的第m个影响因素值。经过无量纲化后得到灰色关联判断矩阵，将相同日期属性的天气特征向量作为比较序列，然后计算每个比较序列与待预测参考序列对应元素的关联系数ρik，计算关联系数的表达式为：

(6)

式中，分辨系数p∈[0,1]，分辨系数p值越大，计算出的关联系数方差越小，区分能力越弱。本文的p值取0.5，并且将比较序列与待预测时段参考序列对应元素关联系数的均值作为关联度指标。关联度指标可以反映各历史时间段与待预测时段参考序列的关联关系。关联度指标的计算公式为：

(7)

依据关联度指标ri，选取与待预测日各时段关联度较大的时段数据作为预测模型的输入。

2.3 基于Stacking策略的机器学习组合预测模型

Stacking策略是一种典型的集成学习方法，能够综合各单一模型的特点而具有一定的优越性。Stacking策略的原理如图2所示。在初始训练集上训练得到初级学习器的预测值，然后在包含初级学习器预测值的新数据集中训练次级学习器，最后将次级学习器的结果输出作为最终的预测结果。相较于对弱学习器的结果做平均或者投票等简单的逻辑处理，Stacking策略是通过训练一个次级学习器将初级弱学习器组合起来，从而能够降低泛化误差，提升预测的准确性。

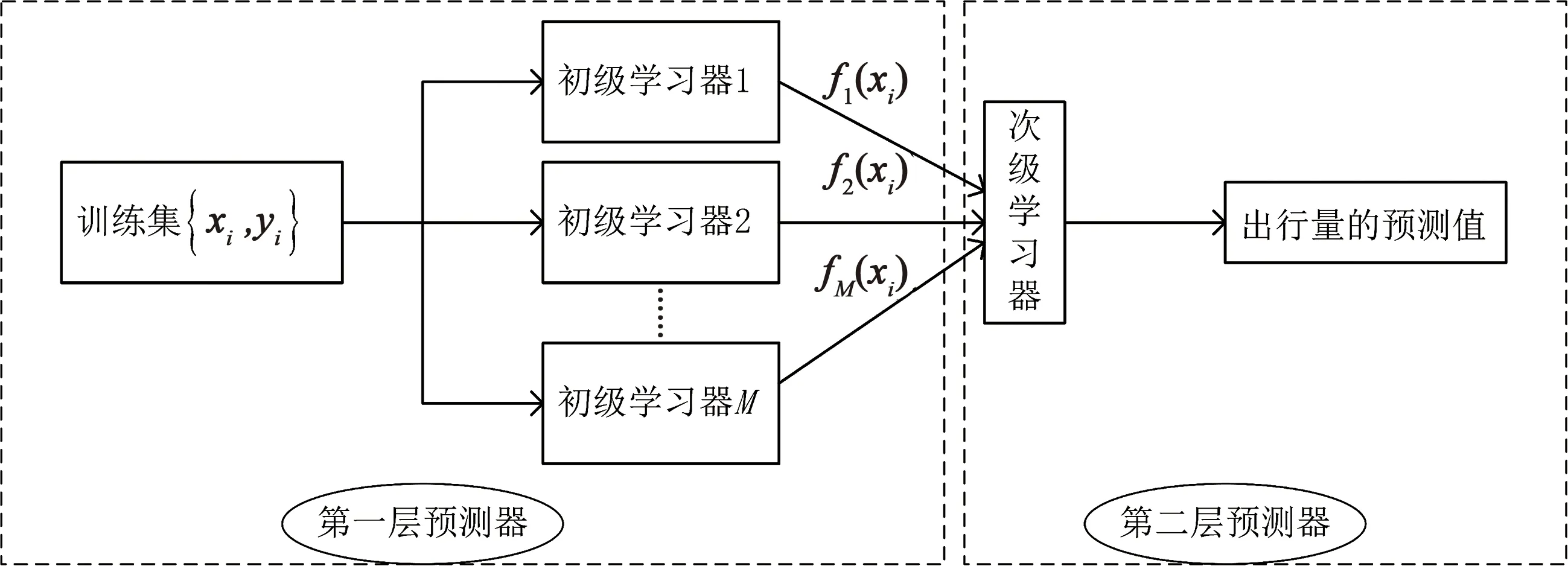
图2 Stacking策略的原理Fig.2 The principle of Stacking strategy

Stacking策略中初级弱学习器的预测性能对最终输出结果的准确性有着重要的影响，按照多样性和准确性的原则，本文选取支持向量回归(SVR)、随机森林回归(RF)、神经网络(NN)和多元线性回归(multiple linear regression, MLR)作为第一层的初级学习器，在初始训练集上训练得到初级学习器的预测值。常见的次级学习器有多元线性回归模型和拟合优度法。拟合优度法根据模型的均方误差(RMSE)的大小来确定各模型的权重系数。模型的权重计算方式如下：

(8)

式中，M为初级学习器的个数。本文提出的Stacking框架集成了多种不同的算法，而且利用灰色关联度对每个初级学习器的输入特征集进行了优化，可获得比单一学习器显著优越的预测精度和泛化性能。

2.4 共享单车出行需求组合预测模型

综上所述，本文提出了基于因果检验和灰色关联分析的需求量组合预测模型，模型结构如图3所示。模型算法的步骤如下：

(1)对天气指标和共享单车需求量进行因果关系检验。在特征选择环节，采用2.1节中的格兰杰因果检验方法，对影响单车需求量的天气指标进行格兰杰因果检验，筛选出通过检验的天气指标，然后对历史样本集进行相似日选取。

(2)基于筛选出的天气指标，采用灰色关联分析法来得到与待预测日各时段相似程度最高且日期属性相同的相似日，形成具有高度相似性的相似日样本集。

(3)在基于Stacking策略的组合模型中，将与待预测日各时段灰色关联度最高的若干相似日的需求量作为输入数据。组合预测模型可以选取支持向量回归、随机森林回归、神经网络和多元线性回归等作为第一层的初级学习器。Stacking 框架集成了多种不同的算法，能够综合各单一模型所具有的特点而具有一定的优越性。该框架利用灰色关联度对每个初级学习器的输入进行了优化，提高了初级学习器的预测性能。

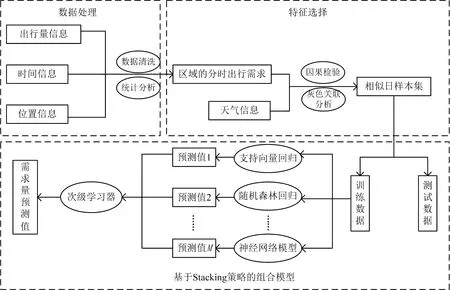
图3 预测模型框架图Fig.3 Predictive model framework

对于评估预测方法效果的指标，采用均方误差(RMSE)、均方根误差(RRMSE)、平均绝对误差(RMAE)和平均绝对百分比误差(RMAPE)来衡量预测值与真实值之间的偏差，其计算公式如下：

(9)

(10)

(11)

(12)

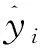
3 实例分析

本文采用北京市2017年5月10日—31日的共计3 214 096条共享单车出行数据，对提出的组合模型进行验证，其中70%的数据为训练集。为了考察共享单车出行需求的空间特性，本文将原始数据根据位置信息进行网格化处理，即将网格单元作为需求量预测模型的基本空间单位。将研究区域划分成了1482个边长为500 m的正方形网格单元。

3.1 需求的空间特性

共享单车的出行需求受地理位置的影响，同一时间不同区域的需求量是不同的。共享单车在某工作日的出行需求的空间分布特征如图4(a)所示。网格单元的颜色越深，表示该区域需求量越大。同一时间，不同区域的需求量差异较大，共享单车的出行需求具有时空性。图4(b)是共享单车需求量分布的直方图，网格单元中共享单车一天的需求量集中在40～100，不同网格区域内出行需求量差异较大。

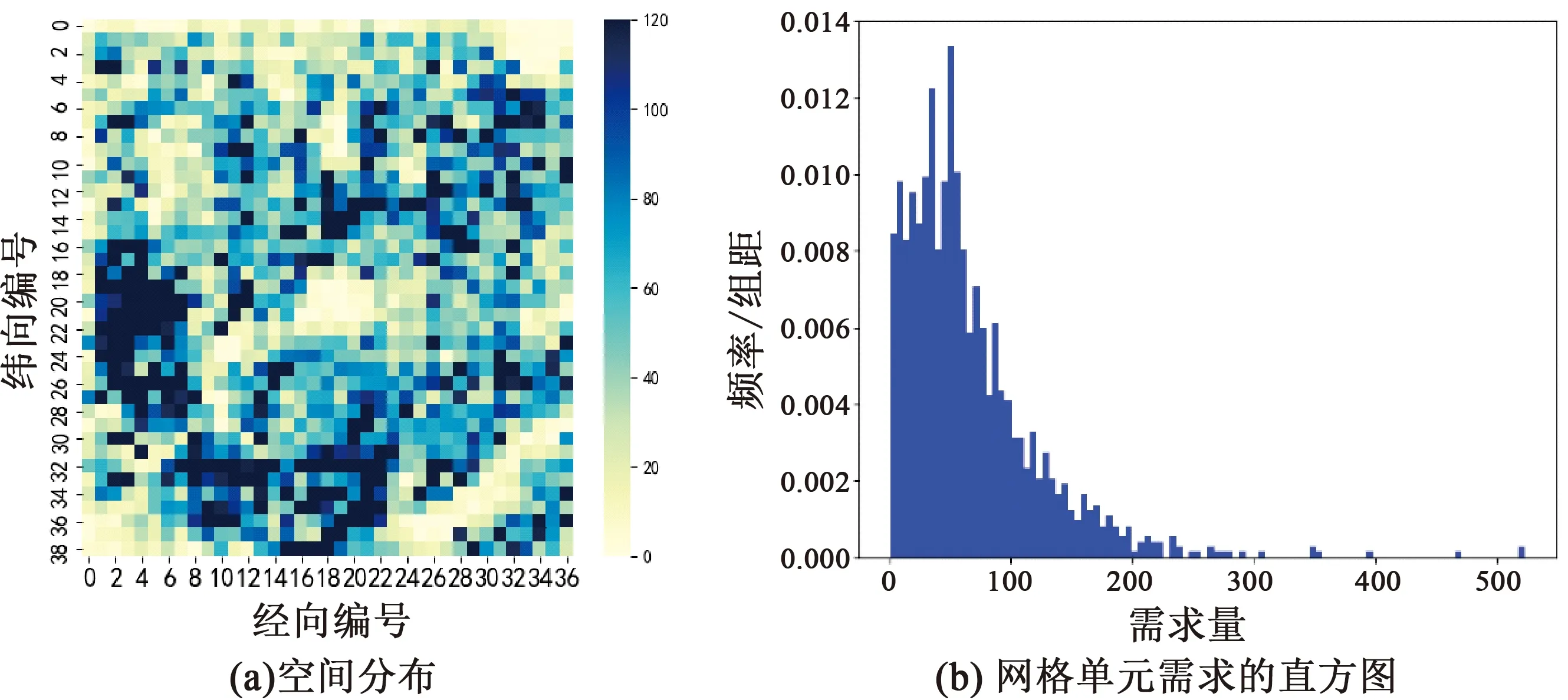
图4 共享单车出行需求量的分布Fig.4 Distribution of demand for shared bikes

根据腾讯企鹅情报对中国共享单车发展情况的调查，62.90%的客户通常在最后一公里使用共享单车[18]。基于真实的共享单车出行数据分析，单次骑行距离的分布如图5所示，90%的骑行距离小于1244 m，说明了共享单车主要用于短途出行，是解决“最后一公里”的主要出行方式。

图5 共享单车出行距离分布Fig.5 Distribution of shared bike travel distance

3.2 相似日确定

在对天气指标格进行格兰杰因果检验之前，采用单位根方法进行平稳性检验。对于非平稳序列，进行差分化处理，直到通过平稳性检验。表3中是在显著性水平α=0.1下，最终通过格兰杰因果检验的指标。

表3 因果分析结果

检验的结果表明，温度、风速、湿度和气压4个天气指标与共享单车出行需求存在统计意义下的格兰杰 因果关系，即有助于预测共享单车出行需求量。利用已通过格兰杰因果检验的天气指标数据，计算待预测日各时段与历史数据之间的灰色关联度，通过灰色关联度的大小来选取待预测日各时段的相似日训练集。图6是采样时刻为5月31日8时与前14个工作日8时的样本集之间的灰色关联度。可以看出，与5月31日8时关联度最大的是5月23日8时的数据，灰色关联度达到0.946。关联度最小的是5月25日同时期的数据，仅为0.66。本文依据关联度指标，各预测时段分别选取5个相似日的历史数据作为预测模型的输入。

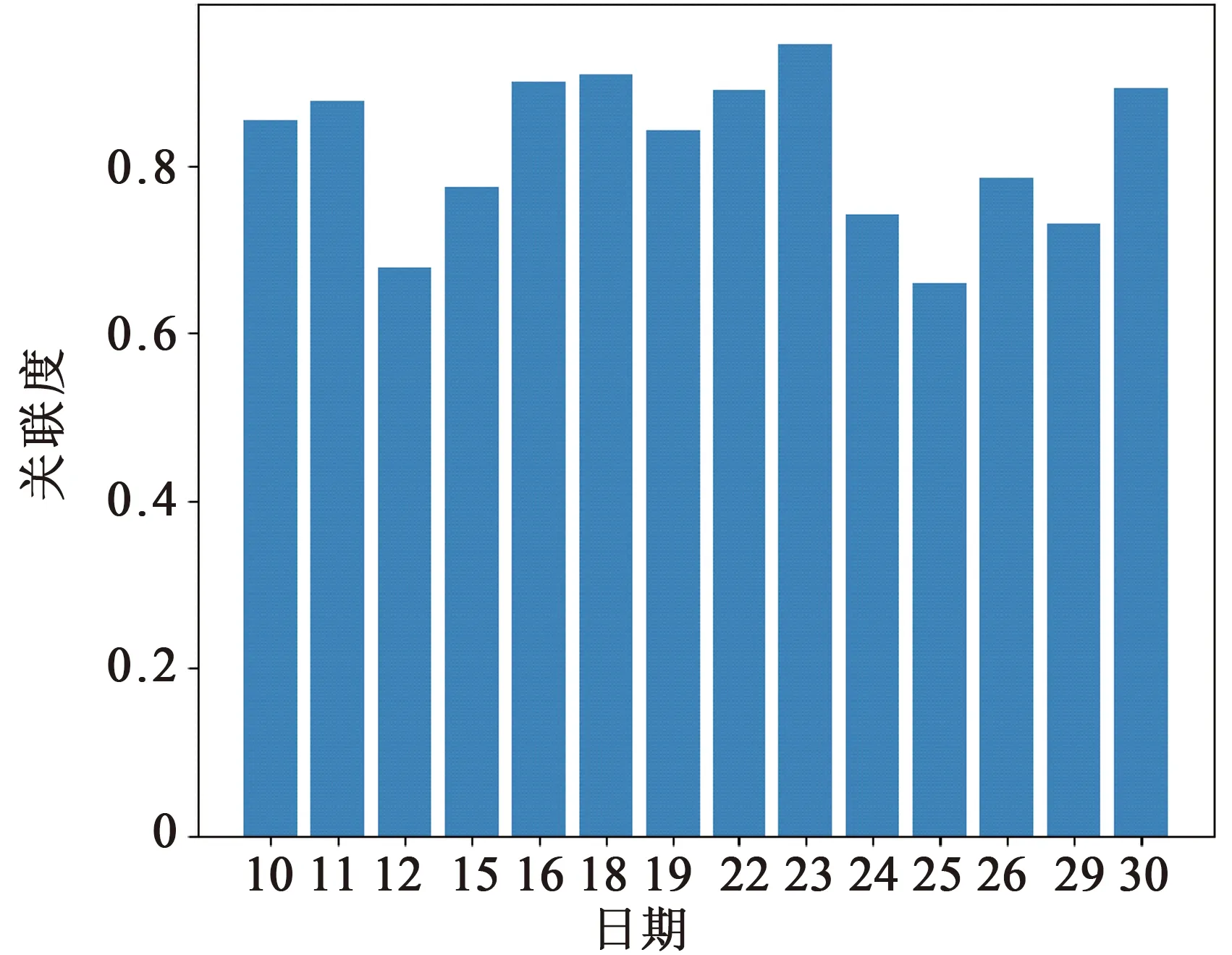
图6 相似日的灰色关联度Fig.6 Gray relevance of similar days

3.3 模型预测精度分析

初级学习器和次级学习器的选择对组合模型的预测精度有着重要影响。本文首先比较了不同组合策略下模型的预测精度。

为了比较不同组合策略的预测精度，确定最优组合模型的结构，本文运用多种组合策略，分别建立需求量预测模型。如表4所示，不同组合策略下的模型预测精度差异较大。策略2采用随机森林和支持向量回归作为初级学习器，策略3在策略2的基础上，初级学习器将随机森林变为了神经网络，并新增了线性回归模型。相较策略2，由于初级学习器的不同，策略3的RMSE下降了20.1%。策略4的初级学习器与策略3相同，但是次级学习器采用拟合优度法。相较策略4，由于次级学习器的不同，策略3的RMSE下降了28%。初级学习器的预测精度对组合模型的预测精度有着重要影响。若初级学习器预测性能较差，可能会造成组合模型的预测精度降低。如相较策略3，策略9新增了随机森林作为初级学习器，但是策略9的RMSE反而增加了6%。说明组合模型的预测精度与学习器的个数没有必然联系，需要深入探究不同学习器的组合策略。由于组合策略3的预测误差最小，因此本文采用的最优组合模型以神经网络、线性回归和支持向量回归为初级学习器，线性回归为次级学习器。

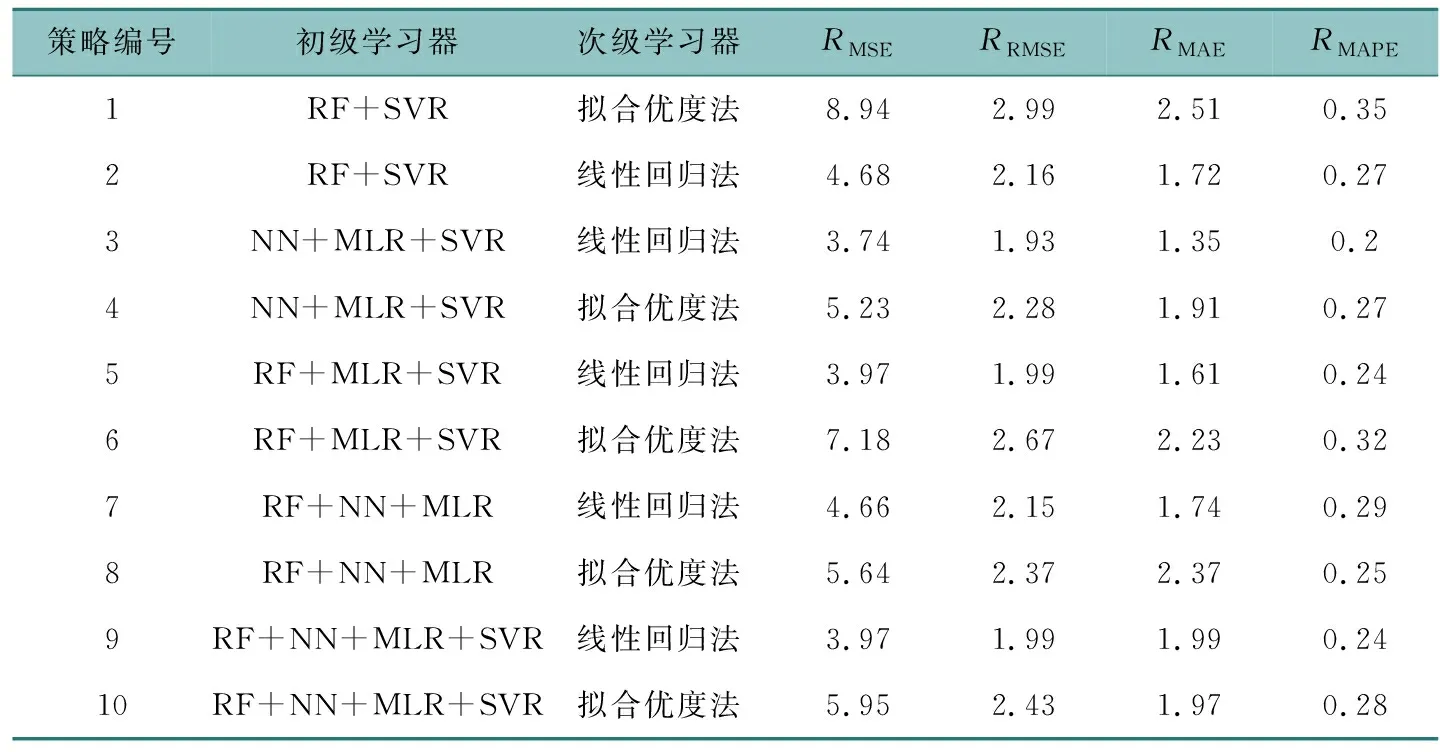
表4 组合模型的预测精度

为了验证相似日选择方法的有效性，本文按照是否采取基于相似日选取的方法，将模型训练输入分为样本集1和样本集2。除了ARIMA模型以外，其余机器学习算法均是选取的与待预测日相同日期属性的样本集。样本集1是基于待预测日相邻前5 d的历史数据，样本集2是基于本文提出的相似日方法选取的关联度最大的5 d历史数据。不同样本输入下的模型预测精度如表5所示。可以看出，相较样本集1，采用样本集2作为输入，随机森林、神经网络、多元线性回归、支持向量回归的预测误差都明显降低，说明采用本文提出的相似日选取方法可以显著提高传统模型的预测精度。另外，相较初级学习器中预测精度最高的神经网络预测模型，本文提出的组合模型的RMAPE下降了9.1%。表明与其他预测基础模型相比，本文提出的组合模型具有更高的预测精度，可为实际车辆调度提供参考依据。

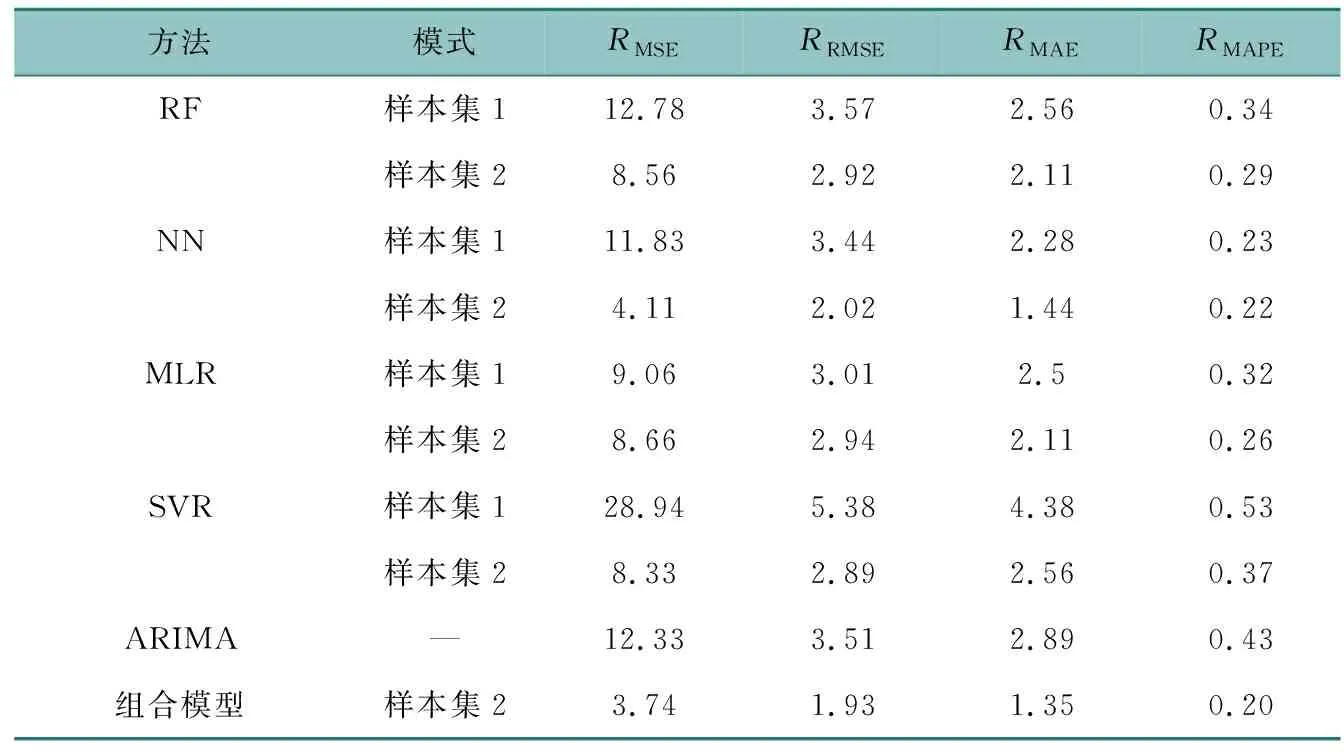
表5 预测精度比较

4 结论

共享单车的需求量预测是提高企业服务质量、效益和用户体验的关键环节。为了筛选出影响单车需求量的关键天气指标，本文引入了格兰杰因果检验方法。为了衡量待预测日各时段与历史日的天气特征向量间的相似性，本文采用灰色关联分析法筛选出了具有高度相似性的相似日样本集。该方法可以有效地对训练样本进行特征选择，减少了模型的计算训练时间并提高模型的泛化能力。在基于Stacking策略的组合模型中，以神经网络、随机森林回归、支持向量回归等算法作为初级学习器，运用多种组合策略，确定的最优组合预测模型综合了各单一模型所具有优势，降低了预测误差并提高了模型的泛化性能。最后以北京市共享单车用户的骑行数据为实验数据进行实例分析，验证了本文模型的准确性。本研究可以用于实际大规模需求预测，为优化共享单车系统布局、实现车辆合理调度提供参考。