基于博弈论组合赋权-TOPSIS模型的排水权分配研究

沈菊琴，赵盟越，王昌盛，张丹丹，詹清清，孙付华

(1.河海大学农业科学与工程学院，江苏 南京 211100； 2.长江保护与绿色发展研究院，江苏 南京 211100； 3.河海大学商学院，江苏 南京 211100； 4.河海大学环境会计与资产经营管理研究所，江苏 南京 211100； 5.南京证券股份有限公司，江苏 南京 210017)

洪水灾害是全球发生最频繁、影响最严重的自然灾害之一[1]，近年来我国频繁出现不同程度的洪水灾害，造成巨大的财产损失和人员伤亡。2020年国家应急管理部发布消息显示：6—7月汛期洪涝灾害导致全国5 480万人次受灾，直接经济损失 1 444.3亿元，其中7月安徽暴雨造成840.2万人受灾，直接经济损失329.9亿元，7月湖北暴雨造成 1 354.63万人受灾，直接经济损失243.23亿元。自习近平总书记提出“节水优先、空间均衡、系统治理、两手发力”十六字治水方针以来，加强防洪管理、降低洪水风险，已成为当前重要的治水思想。

在政策层面，我国制定的《国家防汛抗旱应急预案》《中华人民共和国防汛条例》《中华人民共和国防洪法》等政策条例对洪水预防、调度、救灾等方面进行了规范。在执行层面，地方通过修建水库、建筑堤坝等方式建立洪水防御工事，并适时使用调度机制[2]。但受区域经济条件、地理位置、来水量差异等影响，当洪水量超过流域可调度范围及工程承载量时，各行政区域争相排水，致使区域内矛盾争议不断[3]。目前相关抗洪救灾措施虽可有效降低洪水灾害，却不能解决在洪水排放过程中行政区域间因维护局部利益而抢夺优先排放权所引发的矛盾[4-5]。因此除防洪建设外，政府需建立一种流域整体调节机制，改变洪水无序排放的状况，减少灾害损失，其根本即为在资源(流域可排水总量)有限的情况下，如何协调某时段各行政区域可排放洪水的数值或比例。

灾害发生时，由于各行政区域排水需求大且竞相排水，可排水量成为稀缺资源，为高效、合理配置该稀缺资源，有关专家对排水权进行了研究。立足利益主体角度[6-7]，本文将排水权界定为：暴雨天气下，为减少流域灾害损失、实现区域间排水公平、优化整体防洪效益，本级行政管理机关依据可排水总量及排水需求进行洪涝水排放的权利。

1 文献综述

目前有关排水权的研究较少。于凤存等[8]首次提出排水权的概念，并探讨了排水权配置的公平与效率、可持续发展原则；张劲松等[9]结合洪涝灾害的原因，进一步强调了排水权分配的必要性和可行性。在分配方式的研究方面，徐晓晔[10]基于空间角度进行排水权分配，但大部分学者以因素分析为主。沈菊琴等[11]根据排水权分配目标提出自然、经济、生态等分配指标，并利用混沌优化-投影寻踪法进行排水权分配；Zhang等[12-13]从公平和效率角度，添加了排洪需求、排洪效率等排水权分配影响因素，并将模糊层次分析法与环境基尼系数应用于排水权分配；Sun等[14]基于PSR模型建立排水权分配指标，加入地方的应急措施能力状况，并运用物元可拓模型对排水权进行分配。交易机制上，张凯泽等[15]尝试从博弈角度构建了政府配置排水权后的交易制度。由此可见关于排水权分配的研究现已引起学术界的重视，但目前分配模型均只适用于某种特定情形，急需探索系统完备的分配方法。与排水权相关的水权、排污权等有限资源分配的研究较为丰富，可为排水权分配方法的构建提供思路。

有限资源分配时通常根据分配内容和分配目标的变化构建差异化指标体系：Cetinkaya等[16]以社会、经济、环境为评估指标，作为水资源分配的参考；胡小飞等[17]从人口、经济、环境等角度对排污权初始分配结果进行对比研究；刘佩贵等[18]围绕城市供需排水的特点，在增加基本用水保障原则的基础上构建水权分配指标体系；刘艳丽等[19]以水利益共享为目标，对跨境水资源进行分配，增加保护弱势群体的协调性分配因素。根据分配目标的变化而增减个别指标，虽然可以实现分配结果与分配目标的一致，但指标体系缺乏系统性。

协同学理论能够根据系统内部演变规律和相互影响寻找序参量指标体系，过程更具有系统性和完整性，在水资源分配与评价中得到了有效应用：刘丙军等[20]基于协同学理论将流域分为社会、经济、生态环境子系统，用于水资源配置；吴丹[21]利用协同学理论建立指标体系，评价水资源分配的协同效度；周念清等[22]根据水资源属性，将水资源系统划分为水循环、社会经济、生态环境子系统，并寻找序参量求出各个指标的权重；姚娜等[23]将水资源系统分为水资源、社会经济、生态环境子系统，选取序参量指标对区域水资源可持续利用进行评价。

国内外学者已创建了多种有限资源分配模型并应用于不同的分配情景。Chapman等[24]建立了网格水平衡模型并通过多元回归模型为现有水资源分配建立支持决策系统；为适应不同指标分配，张雷等[25]建立了物元可拓模型对水库初始水权进行分配；为对客观数据进行分配，杨芳等[26]构建了基于投影寻踪混沌优化算法的流域初始水权分配模型；考虑专家主观判断，展金岩等[27]利用模糊层次法解决水权分配问题。但以上方法存在受数学化限制、指标权重考虑不足、计算工作量大或人为性强等缺点，因此本文考虑将TOPSIS逼近理想点来引入排水权初始分配问题，并利用博弈论组合赋权解决赋权片面性的问题。目前TOPSIS法被广泛认可并用于水权分配。刘炳明等[28]运用改进的TOPSIS法对连云港市水权进行分配，结果与实际接近；吴凤平等[29]则组合了模糊优选和TOPSIS法；张学文等[30]将AHP与TOPSIS相结合对宁夏引黄灌区水资源进行初始分配；熊雪珍等[31]采用改进TOPSIS法对“五水共治”理念下4个区域的水资源配置方案展开评价。

基于学者们对排水权及相关有限资源分配的研究分析，本文结合协同学理论寻找排水系统序参量，构建排水权分配指标体系，运用改进的TOPSIS法得出各个行政区域的排水权分配权重。为使指标赋权结果尽可能与实际结果接近，将主观序关系分析法和客观熵权法进行博弈，使权重组合更为合理。

2 排水权分配系统协同学特征及序参量指标选取

2.1 流域排水系统的构成与协同学特征

协同学是研究协同系统从无序到有序演化规律的新兴综合性学科，适用于非均衡的开放、有序系统。将协同学理论应用于其他学科，可以寻找有关系统的影响因素，发挥各个子系统的协同作用。根据排水系统的自然和人为特征，兼顾经济、社会的协同发展，将排水系统分为自然、社会和经济3个子系统。该系统具有协同学的4点表现特征[32]：

a. 多元非线性。排水系统的各个子系统之间是相互竞争、相互协作的关系。相互竞争体现在避免过量水的排放的竞争，这种竞争使系统远离平衡；相互合作体现在其共同目标是使排水系统重新达到有序状态，以实现洪水的合理排放。

b. 动态平衡。当排水量到达使排水系统发生显著质变的临界点时，排水系统的原有平衡遭到破坏，在各系统调解下会走向新的有序平衡。

c. 自发性。排水系统是复杂的大系统，在没有外力作用和外部干预时，各个系统之间也会发生信息的交换，相互影响。

d. 涨落波动性。排水系统会受到诸如气候变化、人类活动等方面的影响，使得排水区域的排放情况发生变化。可见排水系统的涨落波动性与外界环境和人类活动密切相关，且能够在系统结构的动态调整下趋于有序化发展。

2.2 流域排水系统作用机理

排水系统的统一协调是自然、社会和经济3个子系统相互作用的结果。其协同演化分为两个阶段：①当排水量较小时，系统演化主要取决于自然降水量、暴雨重现期、影响调蓄的下垫面构成等因素，优先来水量大、自然条件处于劣势的区域排水，可保证多余水量顺利排放。②当排水量达到甚至超过流域水量容纳能力的临界值，排水能力和排水自由度受到限制，社会经济发展受到影响，系统内的经济贡献度、社会存续现状成为决定性因子。

2.2.1自然子系统

自然子系统是影响整个排水系统平衡的关键因素，主要受限于外界自然降雨情况和区域自身下垫面构成对降水量的调蓄状况，经济和社会发展也对其产生一定影响。自然子系统的降水量影响排水性质和系统走向：降水量较小时，通过径流、汇流过程形成可利用水资源，供经济和社会发展使用，此时排水为“利水”；降水量较大时，无法正常汇集排放的“利水”变为“害水”，产生必要的淹没损失，可能造成经济损失、人员伤亡或者生态破坏。

2.2.2社会子系统

社会子系统是促进排水系统协同发展的重要驱动因素，社会人口环境的稳定、水利设施建设的完善、水生态环境治理的高效可以促进区域经济建设和自然发展的推进，同时地区经济发展和降雨状况等自然因素也影响社会子系统的演变方向。

2.2.3经济子系统

经济子系统的发展可以为社会和自然发展提供保障，其一定程度上受限于自然来水的破坏程度和社会建设对经济的保护状况。当来水量超过排水能力时，社会稳定和经济发展之间存在一定的竞争博弈。一方面，为维持较好的经济发展，可能对社会人口环境、社会生态等造成破坏，导致极大的社会不稳定性。另一方面，只考虑社会稳定，区域经济发展必然受到限制，甚至不可恢复。

2.3 流域排水系统序参量选取

推动排水系统演化的内在动因和决定性因素为序参量[33]，也是影响排水权分配的关键指标。借鉴现有排水权[9]、水权、排污权分配原则[34-35]，排水权分配遵循公平、效率、可持续发展原则。①公平：流域内各区域因自然因素、经济发展水平、社会现状的不同，应对各种洪涝灾害所需的排水权也存在差异，但区域间的排水竞争一直存在，因此分配过程应保证排水的公平。②效率：在暴雨频发期，能够控制和承受洪水的流域属于稀缺资源，而排水权分配的最终目的是使该资源的价值最大化，实现流域综合效益的优化，因而分配过程应综合考虑经济、社会等因素，提高排水的效率。③可持续发展：经济社会的发展和治理应与生态环境的保护同步进行，洪水发生时可能伴随着污水的趁机排放、不达标水流入重要保护水源地等问题，对水体、土壤造成损害，因此排水过程应考虑环境保护和发展问题。在遵循以上原则的基础上，寻找排水系统序参量，构建排水权分配评价指标体系，可使分配结果更贴合实际。

2.3.1自然子系统序参量

自然子系统是排水系统演变方向的最初动力，决定了行政区域自身所需的“净”排水能力。一方面，年降水量，尤其是洪水易发的梅雨期降水量、暴雨重现期决定区域的排水需求，由于降雨时空分部不均，降水越丰沛的区域所得排水权越多；另一方面，区域下垫面构成会调整排水量。河湖、水库等水域体系和地面植被绿化可以容纳和调蓄来水，减少本区域向流域的排水量，相反，建成区等不透水地面会加速来水汇集，增加短时所需排水权。

2.3.2社会子系统序参量

社会子系统在保证生命安全的基础上有助于实现排水权分配的公平与效率。人口密度反映区域社会易害性，是影响排水权分配的首要因素。但在人口构成中，高素质人口能够利用自身经验来抵御洪水风险，降低易害性，而弱势群体应急能力差，需要更多的排水权才能保证生命安全。社会水利建设的加强可扩大整个流域的排水容量、增强排水控制，进而提高排水效率，而社会水利建设通常包含水利建设投资、堤防总长度、排水管道长度、除涝面积等。被污染的排水可能会造成流经区域的土壤污染、水质恶化等生态问题，并进一步对人体健康造成威胁。基于可持续发展和公平视角，应为水质管理能力较好的区域提供较多的排水权。该分配方式将形成激励效应，区域为获得更多的排水权，必然会加强本地污水处理率，加强水质管理等，以提高水质，获得更多的排水权。

2.3.3经济子系统序参量

行政区域经济子系统由两部分构成：一是经济发展潜力，反映现期经济建设情况和未来经济发展贡献值。洪涝灾害通常会造成企业停产、资产损坏、居民生活水平下降等经济问题，尽量减少这些损失的发生，有助于优化流域综合效益。经济发展潜力可通过人均GDP、恩格尔系数、城镇化率、就业率、居民人均可支配收入等确定。二是历史灾害损失，由直接经济损失、农作物受灾面积和受灾人口确定，反映了该地区经济易受损程度和历史受灾状况，代表了该地区在排水权分配中的利益诉求，能够降低排水权分配的不合理性。

选取的排水系统序参量指标类型及释义如表1所示。

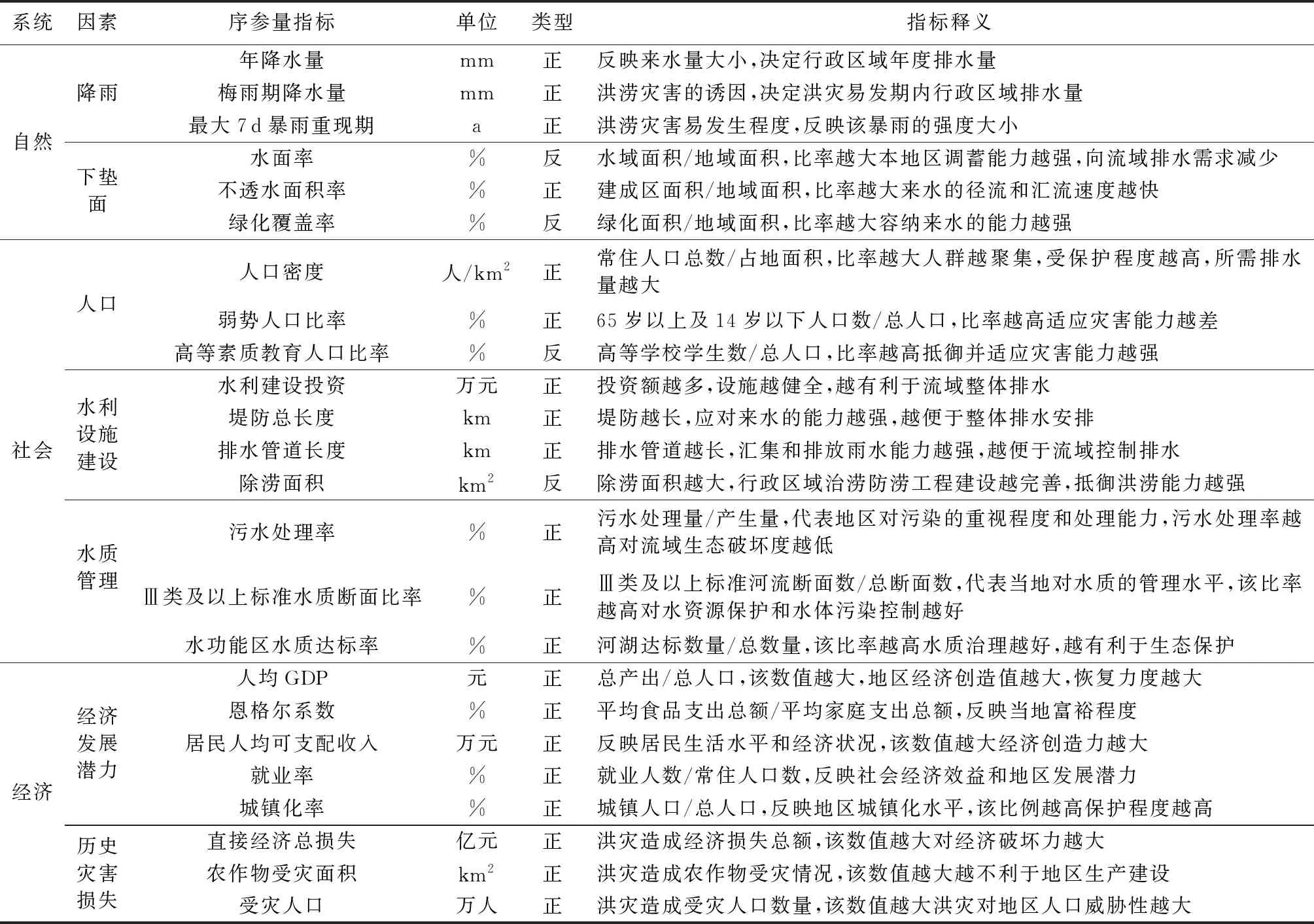
表1 排水系统序参量指标类型及释义

3 排水权分配模型构建

3.1 确定指标权重

3.1.1熵权法确定客观权重

熵权法计量客观权重的核心是通过熵值度量信息量大小。某指标信息量越大则对决策作用越大，反之越小[36]。计算步骤如下。

a. 对每个指标数据进行无量纲化处理，构建决策矩阵Z=(zij)n×m,zij为

(1)

式中：pij为不同地点的分配指标值；n为分配指标数；m为分配地点数。

b. 定义指标熵权ei：

(2)

c. 计算指标客观权重uai：

(3)

3.1.2序关系分析法确定主观权重

排水权分配是子系统竞争博弈的过程，也是对各个影响指标进行重要性排序的过程。采用郭亚军等[37]提出的序关系分析法进行主观赋权。计算步骤如下。

(4)

c. 求解指标权重。根据Ri的理性赋值及权重加和为1的要求，指标主观权重ubi满足：

(5)

3.1.3基于博弈论的组合赋权

博弈论是研究竞争性事物的理论和方法，帮助决策者在竞争事物间权衡并做出理性决策。使用序关系分析法和熵权法的博弈论组合赋权方法，在不同权重间寻找妥协或一致，使指标赋权最优化，计算步骤如下。

a. 确定权重集组合。设有L种方法对指标赋权，则得到权重向量uk=[uk1,uk2,…,ukn](k=1,2,…,L)。记L个权重向量的任意组合为

(6)

式中：ak为线性组合系数；u为一种可能组合权重。

b. 优化对策模型。基于博弈论组合赋权的基本思想，优化的对策模型为

(7)

c. 求最优组合系数αk。式(7)的最优化一阶导数条件可转换为如下方程组，并计算得到组合系数集{α1,α2,…,αL}。

(8)

d. 计算组合权重u*。对αk进行归一化处理，最后得出u*：

(9)

(10)

3.2 计算分配比例流程

a. 构建决策矩阵。将决策矩阵归一化处理，按照正负指标分别计算，构建决策矩阵：

X=(xij)n×m

(11)

将标准化决策矩阵与组合权重相乘，得到加权标准化决策矩阵Y=(yij)n×m，yij为

yij=uixij(i=1,2,…,n;j=1,2,…,m)

(12)

b. 确定最理想加权评价值集合Y+和最不理想加权评价值集合Y-:

(13)

式中：I1为越大越优型指标集合；I2为越小越优型指标集合。

c. 计算每一区域方案与正、负理想解之间的距离:

(14)

d. 确定相对权数。各区域的评价值与最理想评价集合和最不理想评价集合之间的相对权数为

(15)

e. 计算各行政区域分配比例:

(16)

4 案例分析

苏南运河是京杭大运河“黄金水道”的重要组成部分，流经苏州、无锡、常州和镇江4市。近几年苏南运河流域雨涝年份连续出现，各行政区域出于自身利益考虑，纷纷将涝水排向运河，导致运河沿线水位不断增高，加之沿线某些洪水排放管道受阻、太湖水源地环境不可破坏等原因，运河沿岸区域洪水排放与运河自身容纳量有限的矛盾日益突出[13]。为有效实现政府的调度调配，实现苏南运河整体利益的协调发展，利用博弈论组合赋权-TOPSIS的方法对苏南运河苏州、无锡、常州和镇江4市排水权进行合理分配。由于2016年苏南运河发生流域性特大洪水，水位突破历史极值，因而作为典型年进行案例分析。

4.1 指标权重的计算

根据对排水系统机理分析确定的序参量指标，搜集2016年苏州、无锡、常州和镇江4市《统计年鉴》《水资源公报》《环境状况公报》等文件的数据、水文水资源勘测局统计数据见表2。

排水权分配前需要求解各个指标权重。计算客观权重时，首先根据式(1)对表1数据进行预处理，之后运用式(2)(3)求解熵值和指标客观权重。计算主观权重时，邀请专家根据相关信息和历史经验对指标重要性做出理性判断，对其重要性程度之比赋值，并根据式(4)(5)求解。最后根据求解的主、客观数据和式(6)～(10)，计算得出博弈论方法下的组合赋权值。不同方法下排水权分配指标权重结果见表3。各个计算步骤均通过MATLAB编程实现。

表2 排水权初始分配指标样本值

表3 排水权分配指标权重

4.2 各行政区域分配比例的计算

将排水权分配指标数据无量纲化处理后与组合权重相乘，得到加权标准化决策矩阵。通过公式(13)～(16)求出正、负理想解之间的距离后，计算得出博弈论组合赋权-TOPSIS模型下排水权分配比例。同时采用不同赋值方法下的TOPSIS模型对苏南运河进行排水权分配，与博弈论组合赋权-TOPSIS模型下排水权分配进行对比分析，结果见表4。

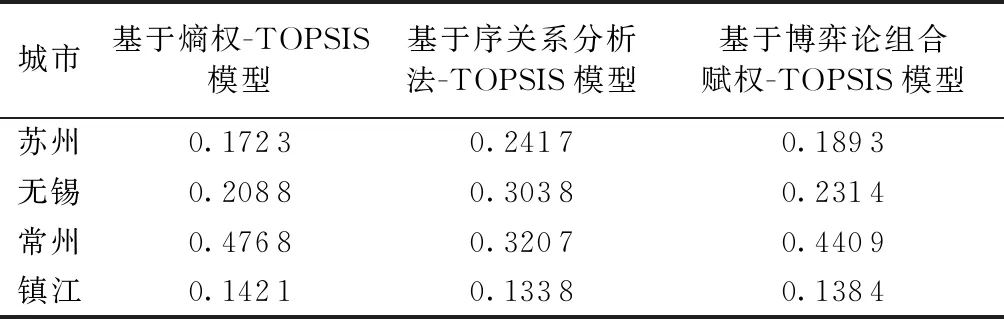
表4 不同排水权分配方法结果对比

4.3 结果分析

根据分析计算，得出苏南运河流域各行政区的排水权分配结果：苏州(0.189 3)、无锡(0.231 4)、常州(0.440 9)、镇江(0.138 4)。从指标博弈论组合赋权结果来看，自然子系统中最大7 d暴雨重现期(0.105 8)、梅雨期降水量(0.097 3)，社会子系统中堤防总长度(0.082 7)，经济子系统中农作物受灾面积(0.200 6)、受灾人口(0.105 1)，均在指标中占有较大比重，是排水权分配过程中需要着重关注的因素。从表1的样本数据可以看出，赋权重较高的重要性正向指标值除社会因素外，在常州、无锡、镇江、苏州4市递减，而社会因素中的堤防总长度苏州极高，最终导致其排水权分配值常州大于无锡大于苏州大于镇江的现象。

为了验证基于博弈论组合赋权-TOPSIS模型下排水权分配的合理性，分别运用不同赋权下的TOPSIS分配方法进行苏南运河流域的排水权分配，分配结果对比见表4。由表4可以看出，基于熵权-TOPSIS模型、基于序关系分析法-TOPSIS模型和基于博弈论组合赋权-TOPSIS模型的分配结果大体一致：排水权分配均为常州大于无锡大于苏州大于镇江的现象，且常州占比较高。分析其原因，主要是历史农作物受灾面积、受灾人口、最大7 d暴雨重现期等主导因素在4个区域间有较大差距，且常州、无锡的数值较高。但3种方法下的分配比例略有不同：①熵权法因过于依赖数据指标，导致数据差值越大，分配比例差距越大的极端现象，不能体现指标间的重要性程度。如排水管道长度和人均GDP数值均较大，但因重要性不同对分配比例会产生不同的影响，但其在熵权法中无法判断。②序关系分析法下邀请专家根据经验和知识进行重要性排序，缩小了4市间的分配差距，但未能挖掘出数据间的内在规律且存在一定主观性。③博弈论组合赋权法下的分配结果综合了主、客观赋权的优点，既关注指标的重要性，又能体现数据的内在规律，使得分配结果更加合理。

排水权的分配结果是建立在区域自然、社会和经济协调发展的基础之上。对于苏南运河流域而言，自然降雨状况和历史灾害损失、水利设施建设在其中起到尤为重要的引导作用。而污水处理、就业率等指标的引导作用较弱。可见，在洪水雨涝自然灾害情况下，降雨状况和易受害程度是排水权分配中需着重考虑的因素。

5 结 论

在分析排水权分配必要性的基础上，本文借鉴了水权、排污权等有限资源的分配方法，通过协同学理论寻找排水系统中自然子系统、社会子系统、经济子系统的序参量指标，构建博弈论组合赋权-TOPSIS模型对排水权进行分配，并将其运用于苏南运河流域苏州、无锡、常州和镇江4市进行分配研究，得如下结论：

a. 排水系统实现统一协调效应的核心是对自然子系统、社会子系统和经济子系统的整体调控。不同时段的排水系统呈现不同的宏观现象，系统中的序参量指标决定着排水权分配的结果。通过机理分析共选取24个影响指标，这些指标易于测量，便与获取，提高了分配结果的准确性。

b. 构建的博弈论组合赋权-TOPSIS模型排水权分配方法，弥补了主观赋权的随意性和客观赋权数据依赖性的缺点，使分配结果更加合理。案例分析中用基于熵权-TOPSIS模型、基于序关系分析法-TOPSIS模型和基于博弈论组合赋权-TOPSIS模型3种赋权方法对苏南运河流域镇江、常州、无锡和苏州4市的排水权分配结果进行对比，结果显示组合赋权方法下的分配结果综合了专家经验及客观数据，更具有借鉴意义。

c. 排水权分配是以极端天气发生的特定期间为前提，目标是实现流域损失最小化、效益最大化。案例分析中常州的分配比例远高于苏州、常州、镇江，分析其原因一是因为最大7 d暴雨重现期等指标赋值比例较高，二是因为常州的多数样本数值远高于苏州、无锡、镇江。该分配结果符合排水权分配的目标，验证了该分配方法的可行性。

d. 博弈论组合赋权-TOPSIS模型的排水权分配方法为流域排水权初始分配提供了新思路，案例分析的结果为完善防汛排水体系提供了方向和参考。公平高效的排水权分配方式可以为区域减少洪涝损失，并为排水权交易鉴定基础。