基于SFA-ESDA的长江三角洲地区全要素水资源利用效率研究

王济干，李颖秋

(河海大学商学院，江苏 南京 211100)

随着工业化与城市化进程的加速，水资源短缺问题日益严重[1-2]。对此，联合国亚洲及太平洋经济社会委员会发布了一份调查报告，该报告指出：近年来亚太地区经济体得到了飞速发展，但其所面临的水资源匮乏仍然是最严峻的挑战之一[3]。

中国的水资源总量相对丰富，但大量的水资源不可利用，实际可利用水资源量不足总量的30%；且中国的人均水资源量远远不及世界平均水平，仅为其1/4左右[4]。根据水利部预测，2030年我国供水能力与用水总量严重不匹配，实际可利用的淡水资源已经濒临合理利用的边界值，水资源开发难度很大[5]。中国的工业化与城市化进程日益加快，如果水资源问题得不到足够重视，水资源问题将会成为社会发展进程的巨大障碍[6]。除此之外，我国水资源质量问题也令人担忧。据监察部门统计，近几年每年至少会发生1 700起的水污染事故。全国饮用水水源地水质不安全问题频发，仅城镇就已经威胁了1.4亿人。

2011年，中共中央国务院发布的一号文件《中共中央国务院关于加快水利改革发展的决定》中要求水资源管理制度在最严格的条件下实行。该文件还提出了“三条红线”的概念，其中一条红线是为了控制用水效率，体现了国家遏制用水浪费的决心[7]；2014年习近平总书记发表的讲话中，从全局与战略角度提出了水安全问题；2016年，中共中央办公厅、国务院办公厅联合印发了《关于全面推行河长制的意见》，该意见明确将水资源的保护、治理放在重要位置，要求各地区、各部门修复和改善水的生态环境。这些相关政策的推行，表明水资源治理问题已经得到了国家的高度重视[7]。

长江三角洲地区具有人口密度大、经济发达和城市化水平高的特点，是我国经济社会中备受关注的地区之一[8]。另外，该地区江海交汇、水道纵横、湖荡棋布、河网密度大，且常年降雨量充沛，水资源相对丰富。但由于该地区水资源分布不均、时空变化大，其组合很不平衡。长江三角洲地区人均当地水资源量为774.90 m3，仅为全国平均水平的1/3，其中江苏省和上海市属于水资源紧缺地区，人均水资源量分别为245.85 m3和457.55 m3[9]。目前，长江三角洲地区因禽类养殖问题频发水域污染，而农业灌溉和生产、生活造成的水污染也日益严重。这些水污染事件的发生不仅严重破坏了原有的生态环境，而且对当地居民的用水安全造成威胁。如2007年太湖暴发的蓝藻事件，造成居民饮水出现危机。之后政府投入大量的人力、物力和财力对太湖进行治理，情况依旧严峻。

长江三角洲地区快速的城市化进程，一方面满足了其经济发展的要求，但另一方面却加剧了水资源和水环境问题，进而对人类赖以生存的环境造成威胁。本文对水资源利用效率进行了研究，以期通过提高水资源利用效率缓解水资源短缺的问题，达到水资源可持续利用的目标，以促进水资源与经济社会的协调发展，并推进长江流域大保护战略的进一步发展。

1 文献综述

水效率被定义为每单位用水量产生产品的经济价值。根据这一定义，有关学者研究了农业和整个经济水平的水效率[10-12]。如Mo等[10]根据单位用水量的农作物产量来考察华北平原的水分利用效率及其对农业的影响；李世祥等[11]通过构建一系列经济-水指数对水资源利用效率在中国是否存在区域差异进行研究。然而，这些研究中的水效率都属于单因素效率，只考虑了水作为产生输出的单一输入而忽略了其他关键输入。事实上，单独用水作为投入不能产生任何产出，必须与其他投入(如劳动力、资本)一起投入，才能产生经济产出。此外，由于不同生产要素之间存在替代效应，因此单因素水效率评估不够全面，可能导致误导性结论。

系统中各个要素的综合生产率被称为全要素生产率，可以表述为总产出量与全部生产要素投入量之比，其中，全部生产要素主要包括资本、劳动力及土地，但通常分析时都略去土地。在一项开创性工作中，Hu等[13]将水输入纳入全要素生产框架，以构建全要素水资源利用效率指数，该指数定义为最佳用水量与实际用水量之比。孙冬营等[14]采用考虑期望产出和非期望产出的SBM模型，从投入产出角度对全要素水资源利用效率进行测度。就目前的研究而言，考虑水资源利用效率时纳入全要素生产框架的主要有两种评价方法，数据包络分析(DEA)法和随机前沿分析(SFA)法。

DEA作为一种多因素效率评估技术已被广泛应用于处理水效率评估问题[15-22]。Hu等[13]利用DEA构建了水调整目标比率指数，计算出生活和生产用水效率并分析了区域差异。随着时间的推移，DEA也有了一些改进。孙才志等[15]用DEA法计算出1997—2007年10年间中国31个省市(区)水资源利用相对效率，并且运用探索性空间数据分析法(exploratory spatial data analysis， ESDA)初步探索了其时空差异变化规律。而Yang等[20]利用DEA-SBM模型分析了我国水资源能源全要素效率；邓兆远[22]则利用三阶段超效率SBM-DEA模型分析了我国环渤海地区的用水效率。SBM-DEA模型包含了非期望产出，属于考虑非期望产出的全要素水资源利用效率测度模型。

SFA方法由Aigner等开发并已广泛应用于能源和环境效率评估领域[23-28]。Xu等[24]采用基于Shephard能量距离函数的SFA模型来分析2001—2010年中国的全要素水资源利用效率及其影响因素；Du等[27]利用潜在类随机前沿方法测量异质技术下的能源效率并应用于中国能源经济；邢贞成等[28]采用基于Shephard生态距离函数的SFA模型来分析2007—2015年中国区域生态效率及其决定因素。

综上所述，对水资源利用效率进行测度或评价的研究主要分为以下几个类型：第一类是单要素水资源利用效率的测度，该方法考虑不够全面，容易导致误导性的结论；第二类是全要素水资源利用效率的测度，主要有DEA和SFA两种方法；第三类是考虑非期望产出的全要素水资源利用效率的测度。无论是DEA还是SFA都是既可以单独考虑期望产出，又可以考虑期望产出和非期望产出，其中，考虑非期望产出得出的结果更严谨。很明显，DEA作为一种流行的非参数技术已被广泛应用于全要素水资源利用效率的分析，它在边界上没有任何功能形式，从而避免了模型错误。尽管DEA具有优势，但它没有考虑统计噪声，这可能使结果对数据质量非常敏感，甚至导致效率估计偏差[29]。鉴于DEA可能会导致偏差，需要叠加别的方法来避免误差，所以一些学者把目标转向了基于距离函数的SFA法。作为典型的参数边界方法，SFA的所有观测都是在边界两侧，并且可以将随机误差与无效率差异分开[30]，只需一步便可研究技术效率及其影响因素。所以本文选取SFA方法来研究全要素水资源利用效率。

2 研究方法

2.1 Shephard水距离函数

考虑构建一个距离函数，首先需要定义一个生产技术集。通过该过程，每个决策单元DMU(即长江三角洲地区每个城市)都将资本存量(K)、劳动力(L)和水资源(W)作为输入来生产，GDP(Y)和废水(B)分别作为单个理想输出和不希望的输出即非期望产出。从概念上可以将生产技术集定义为

T={(K，L，W，Y，B)∶(K，L，W)产出(Y，B)}

(1)

式中T为在依靠生产技术的前提下，一定输入产生的输出的所有可能集合。在生产理论中，通常假设T满足以下性质：①没有输入就没有产出；②T是有限的；③T有界。

因此，根据Zhou等[29]开发的Shephard能源距离函数，定义一个用于水的Shephard子矢量输入距离函数(称为Shephard水距离函数)：

DW(K，L，W，Y，B)=sup{β：(K，L，W/β，Y，B)∈T}

(2)

式(2)试图估计W的潜在减少极限，同时将输入-输出组合保持在式(1)定义的生产技术中，它衡量的是用水可以减少的程度。因此，W/DW(K，L，W，Y，B)为假设水用量。将全要素水资源利用效率(total factor water efficiency， TFWE)定义为最佳用水与实际用水之比，由此，全要素水资源利用效率计算公式为

(3)

式中E为全要素水资源利用效率。

由式(3)可以看出，全要素水资源利用效率等于Shephard水距离函数的倒数。全要素水资源利用效率的定义意味着它小于或等于1，较高的分数意味着更好的水效率性能。

2.2 SFA测算模型

在经验应用中，Shephard水距离函数可以在非参数或参数框架内估计。而柯布-道格拉斯函数和超越对数函数是SFA生产函数常选用的两种形式，两者比较而言，后者的表现形式限制少，可以更灵活地降低相应的估计偏差。

因此，按照Du等[27]的研究，采用Translog函数来指定Shephard水距离函数，描述为

lnDw,t(Ki,t，Li,t，Wi,t，Yi,t，Bi,t)=β0+βklnKi,t+

βllnLi,t+βwlnWi,t+βylnYi,t+βblnBi,t+βkk(lnKi,t)2+

βll(lnLi,t)2+βww(lnWi,t)2+βyy(lnYi,t)2+

βbb(lnBi,t)2+βkllnKi,tlnLi,t+βkwlnKi,tlnWi,t+

βkylnKi,tlnYi,t+βkblnKi,tlnBi,t+βlwlnLi,tlnWi,t+

βlylnLi,tlnYi,t+βlblnLi,tlnBi,t+βwylnWi,tlnYi,t+

βwblnWi,tlnBi,t+βyblnYi,tlnBi,t+βtt+βttt2+βkttlnKi,t+

βlttlnLi,t+βwttlnWi,t+βyttlnYi,t+βbttlnBi,t+vi,t

(4)

式中：t为时间；i为省市；Ki,t、Li,t、Wi,t分别为i城市在t年的固定资产投资、劳动力和水资源投入；Yi,t、Bi,t分别为GDP和废水产出；vi,t为一个随机变量，考虑到统计噪声，假定其服从标准正态分布；β为要估计的参数。

经过适当的数学推导，得

ln(1/Wi,t)=β0+βklnKi,t+βllnLi,t+βylnYi,t+

βblnBi,t+βkk(lnKi,t)2+βll(lnLi,t)2+βyy(lnYi,t)2+

βbb(lnBi,t)2+βkllnKi,tlnLi,t+βkylnKi,tlnYi,t+

βkblnKi,tlnBi,t+βlylnLi,tlnYi,t+βlblnLi,tlnBi,t+

βyblnYi,tlnBi,t+βtt+βttt2+βkttlnKi,t+βlttlnLi,t+

βyttlnYi,t+βbttlnBi,t+vi,t-μi,t

(5)

其中μi,t=lnDw,t(Ki,t，Li,t，Wi,t，Yi,t，Bi,t)

是一个非负变量，说明水的无效率。

因此，将式(5)作为导出的一个SFA模型，用来计算Shephard水距离函数。

2.3 ESDA模型构建

采用ESDA对长江三角洲地区三省一市26个城市的全要素水资源利用效率进行空间相关分析，运用该方法数据的空间分布模式能够被注重发现并被可视化[16]。

ESDA法主要是利用空间自相关指数来实现其空间关联测度，常用的指数有Moran的I指数(即莫兰指数)和Geary的C指数，本文采用Moran的I指数。Moran的I指数又可分为Global Moran’sI(全局莫兰指数)和Local Moran’sI(局部莫兰指数)，前者主要探索整个区域的空间分布特征，而后者主要探索子区域的空间分布格局。利用GeoDa软件可展现Moran散点图和LISA聚集图，则全要素水资源利用效率的分布规律可以借助可视化后的图示来研究。计算公式为[16]

(6)

(7)

式中：n为空间单元数；Wij为空间相邻权重，是空间权重行标准化形式；xi为i市水资源利用效率；Zi为i观测值的标准化。一般在计算时，为计算空间权重，邻接标准或距离标准被广泛运用，本文选用邻接标准。具体规则为：若i与j相邻，Wij的取值为1，若不相邻，则取值为0。

如果局部莫兰指数和Zi均为正值，则i将落于H-H范围；如果局部莫兰指数和Zi均为负值，则i将落于L-H范围；如果局部莫兰指数计算为正而Zi为负，则i将落于L-L范围；如果局部莫兰指数计算为负而Zi为正，则i将落于H-L范围[24]。Moran’sI变化于-1～1之间，当Moran’sI=0时代表空间相关不显著，Moran’sI>0时代表空间正相关，而Moran’sI<0为空间负相关。

2.4 指标选择和数据来源

2.4.1指标选择

考虑数据的可获得性，以长江三角洲地区三省一市的26个城市为决策单元，采用这26个城市的面板数据，研究2006—2015年长江三角洲地区全要素水资源利用效率。在构建的水距离函数中，投入指标包括自然资源、劳动力和资本，产出指标为期望产出指标GDP和非期望产出指标废水。具体衡量标准说明如下。

a. 投入指标：①采用工业用水总量来衡量自然资源投入指标；②采用工业从业人数来衡量劳动力投入指标；③采用固定资产投资来衡量资本投入指标。

b. 产出指标。①采用GDP作为期望产出指标。为了消除价格变动的影响，使用GDP平减指数将历年现价GDP转化为2006年不变价格。②采用工业废水排放量作为非期望产出指标。

2.4.2数据来源

选取长江三角洲地区2007—2016年10年间26个城市的数据(表1)为面板数据，数据来源于《中国统计年鉴》和《中国城市统计年鉴》。

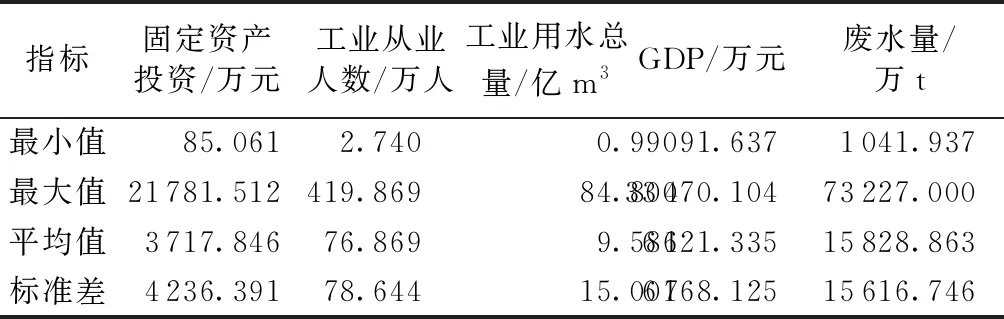
表1 投入与产出的描述性统计(2006—2015年)

3 结果与分析

3.1 长江三角洲地区水资源利用效率测算结果及分析

利用Frontier V4.1求解式(5)，对2006—2015年我国长江三角洲地区26个城市的全要素水资源利用效率值进行评估，并对结果进行总结。从表2可以看出，一方面，舟山市的平均全要素水资源利用效率得分最高，其次是宁波、台州、扬州、上海。这5个城市的平均全要素水资源利用效率得分都在0.9以上，其中浙江省3个城市，江苏省和上海市各占1个席位，而安徽省没有城市的全要素水资源利用效率在0.9以上，说明浙江省在长江三角洲地区水资源利用效率相对较高，而安徽省则有所逊色。而包括镇江、池州、南通、金华、合肥、湖州、嘉兴、盐城等城市在内的13个城市的全要素水资源利用效率均高于0.8，说明长江三角洲地区三省一市的26个城市中，有1/2的城市全要素水资源利用效率较高。其中，浙江省、江苏省和安徽省分别有6个、4个和2个城市均值在0.8以上，而长江三角洲地区26个城市中浙江省只有8个，进一步说明了浙江省在长江三角洲地区水资源利用效率相对较高。另一方面，滁州市的平均全要素水资源利用效率得分最低，其次为杭州、马鞍山、泰州和宣城，这5个城市的平均水资源利用效率得分均低于0.6，其中，安徽省占3个城市，而浙江省和江苏省各占1个城市。由此可见，安徽省在长江三角洲地区水资源利用效率稍有逊色。

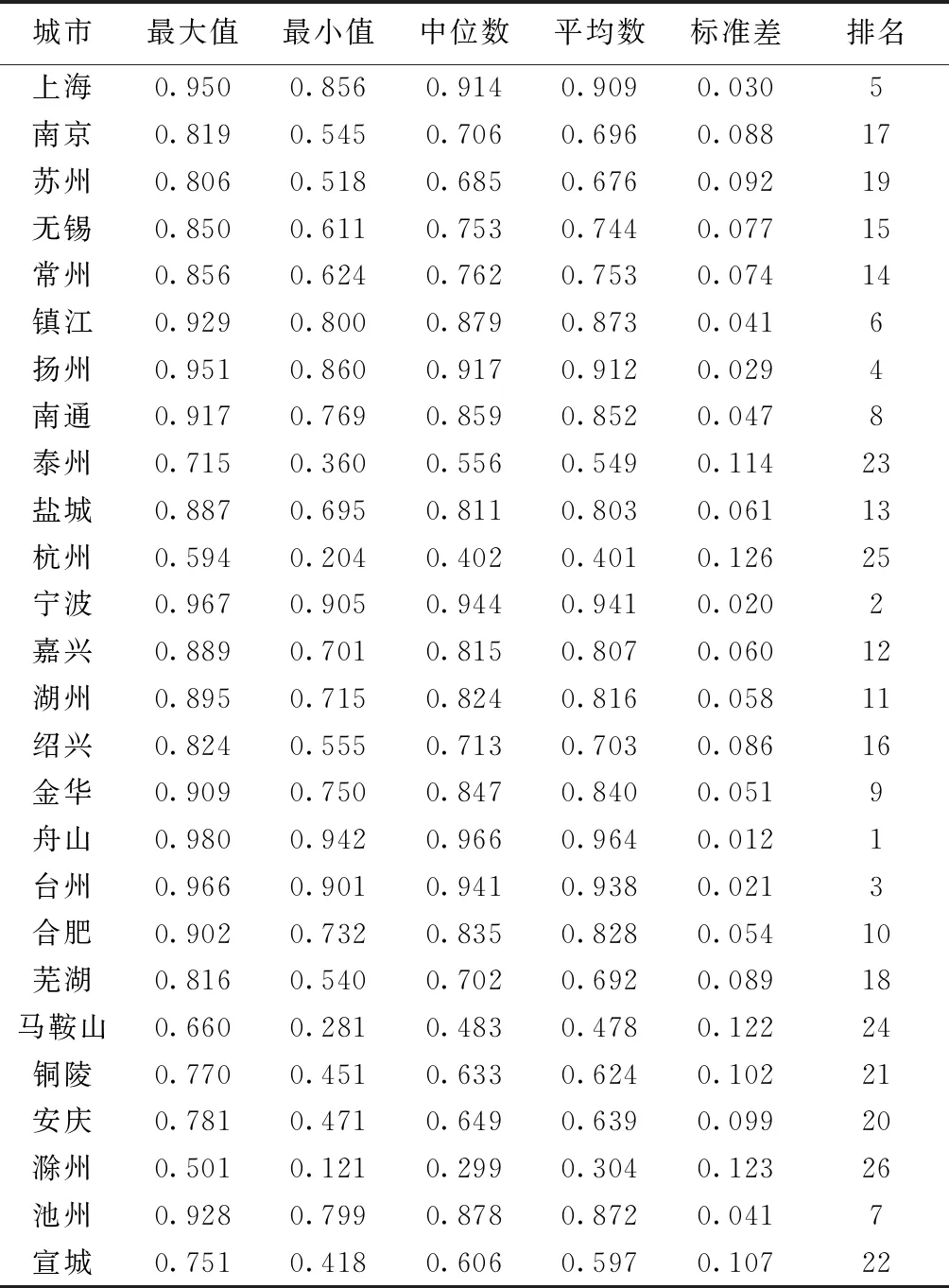
表2 全要素水资源利用效率值(2006—2015年)

3.2 时空演化

图1为我国长江三角洲地区26个城市全要素水资源利用效率的时间变化趋势。从横向角度看，从2006—2015年，长江三角洲地区全要素水资源利用效率值的发展轨迹一直都是稳步上升。其中，上海市和浙江省的上升幅度不大，主要这两个省(市)全要素水资源利用效率的得分较高，平均涨幅在0.1。而安徽省的全要素水资源利用效率的得分上升趋势较快，因为其全要素水资源利用效率总体偏低，涨幅在0.3。从纵向上看，从2006—2015年，上海市全要素水资源利用效率总体显著高于安徽省。这充分说明，上海市具有经济和技术优势，可以更有效、高效地利用水资源，从而更接近生产前沿。从表3可以看出得分排名前三的城市都是浙江省的，但从图1来看，浙江省的全要素水资源利用效率却总体低于上海市，这主要是因为上海市只有一个数据，而浙江省的数据是8个城市的平均数。

图1 2006—2015年长江三角洲地区全要素水资源利用效率变化趋势

图2为我国长江三角洲地区全要素水资源利用效率在2006年、2009年、2012年和2015年的分布模式。从图2可以发现，长江三角洲地区的全要素水资源利用效率得分呈上升趋势。从2006年的分布来看，约1/4的城市全要素水资源利用效率得分低于0.501，分别是滁州、马鞍山、铜陵、安庆、宣城、泰州和杭州。这些城市中江苏省和浙江省均只占1个，其余5个城市都属于安徽省。而到2009年，只有滁州、马鞍山、泰州和杭州4个城市全要素水资源利用效率得分仍较低，说明安徽省铜陵、安庆和宣城3个城市有意识地提高了水资源利用效率。而2012年，长江三角洲地区只剩杭州市和滁州市的全要素水资源利用效率得分较低，说明安徽省和江苏省均在努力提高水资源利用效率。到2015年，26个城市中只剩滁州市的全要素水资源利用效率得分较低，并且该城市的得分一直小于0.501，说明该市没有与安徽省其他城市共同进步。

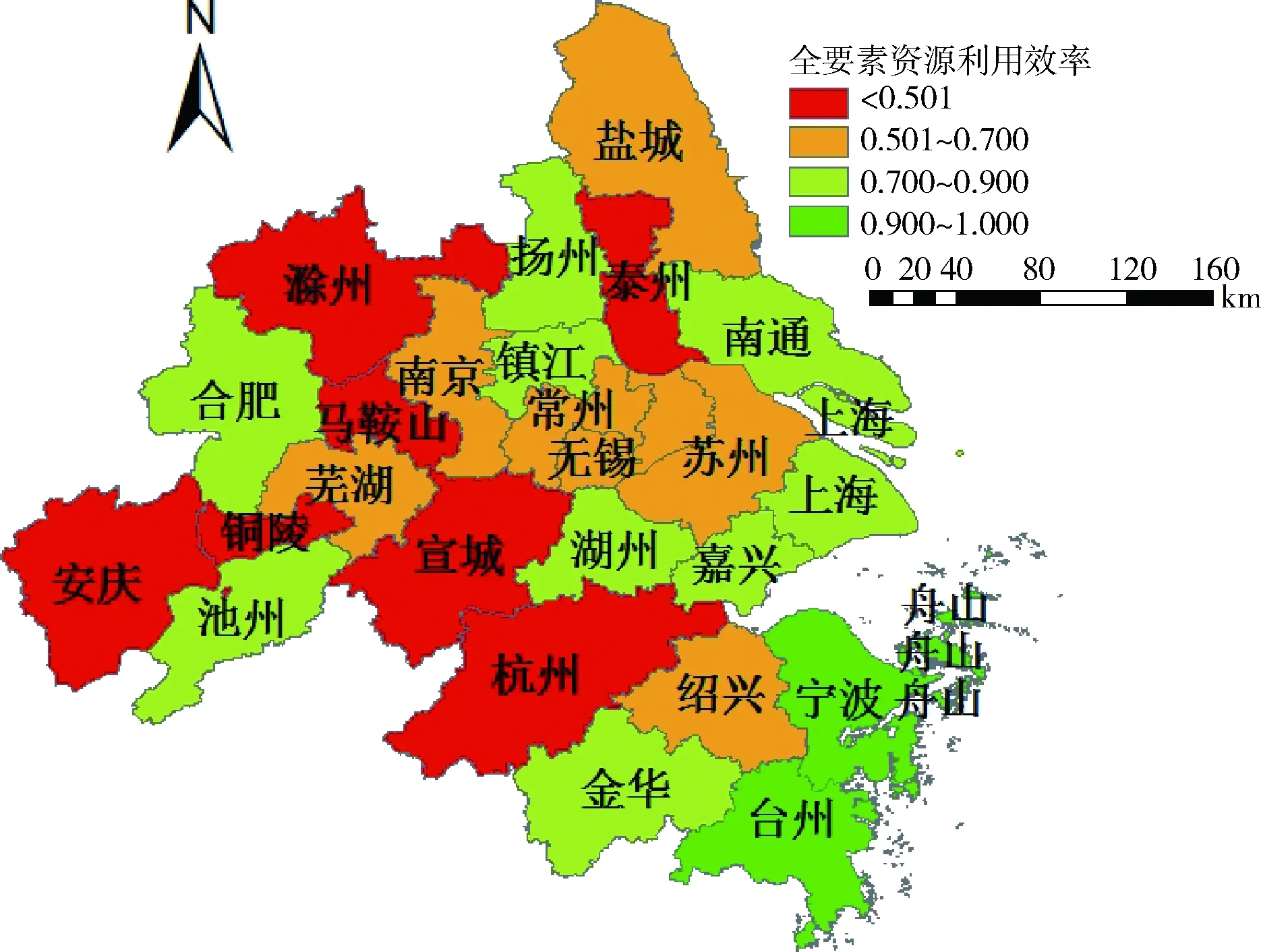
(a) 2006年

(b) 2009年

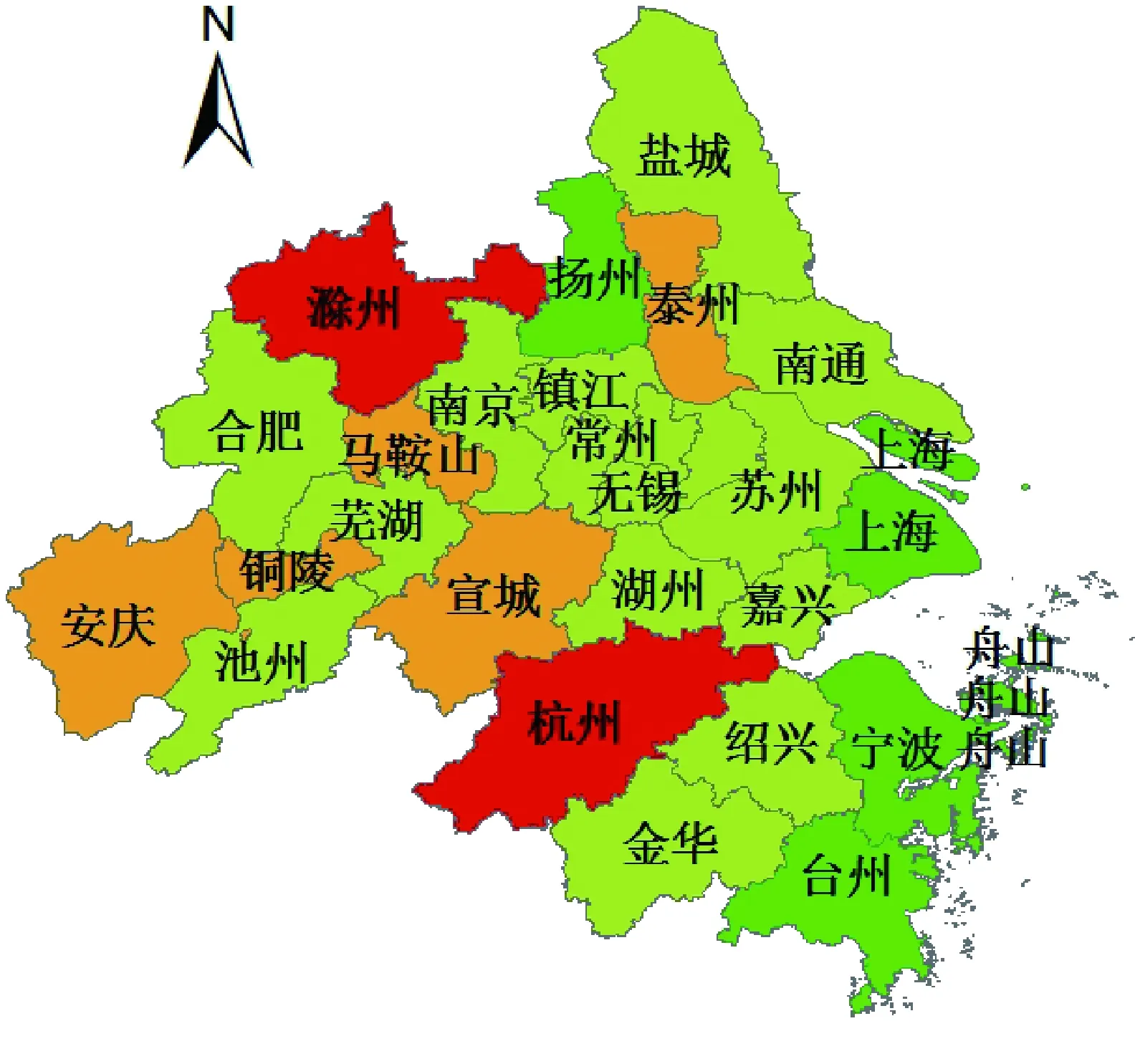
(c) 2012年

(d) 2015年

显然，全要素水资源利用效率较高的地区在2006年主要集中在舟山市、宁波市和台州市；2009年则增加了江苏省的扬州市；2012年增加了上海市；到2015年，效率较高的城市明显增多，得分在0.9以上的城市接近1/2。其中，宁波、台州和舟山3个城市是2006—2015年期间全要素水资源利用效率一直保持在0.9以上的城市，从地理位置上来看这3个城市相邻，表明空间集群存在的可能。效率较低的地区主要集中在滁州市、马鞍山市、泰州市和杭州市。其中，杭州是一个比较特别的城市，其经济发展水平与全要素水资源利用效率得分不成正比。杭州的全要素水资源利用效率得分在前3阶段均低于0.501，虽然在2015年有所提高，仍属于效率较低的城市，说明该城市采取了相关措施以提高水资源利用效率，但效果甚微。从横向来看，安庆、铜陵、宣城和泰州4个城市在研究期间全要素水资源利用效率有较大增长，得分均从小于0.501提高到0.7～0.9的范围，而湖州市和嘉兴市则没有显著变化，得分一直处于0.7～0.9的范围内，其中安庆市和铜陵市在地理位置上相邻，表明可能存在空间聚集。

3.3 长江三角洲地区水资源利用效率的空间特征分析

3.3.1全局空间自相关分析

为了进一步探索长江三角洲地区水资源利用效率的空间分布特征，利用GeoDa软件对测算的水资源利用效率进行莫兰指数检验，结果如表3所示。根据一般规则，Moran’sI>0，说明长江三角洲地区水资源利用效率整体存在空间自相关性；统计量Z>1.96，说明长江三角洲地区水资源利用效率在空间上呈现聚集特征，这在一定程度上也反映出长江

表3 长江三角洲地区全要素水资源利用效率的Moran’s I检验

(a) 2006年

(b) 2009年

(c) 2012年

(d) 2015年

三角洲地区三省一市26个城市的水资源利用效率存在一定的差异。

3.3.2局部空间自相关分析

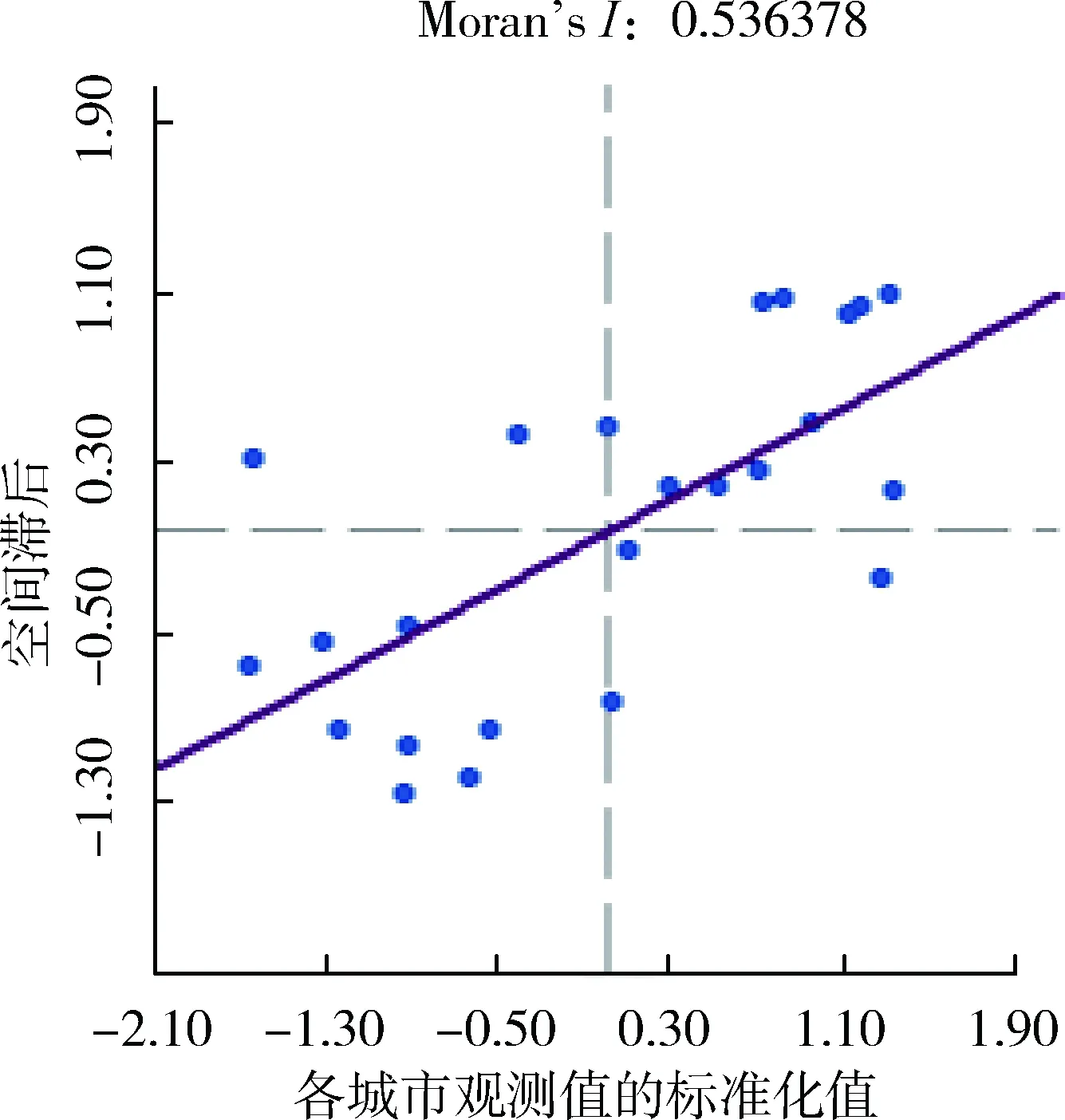
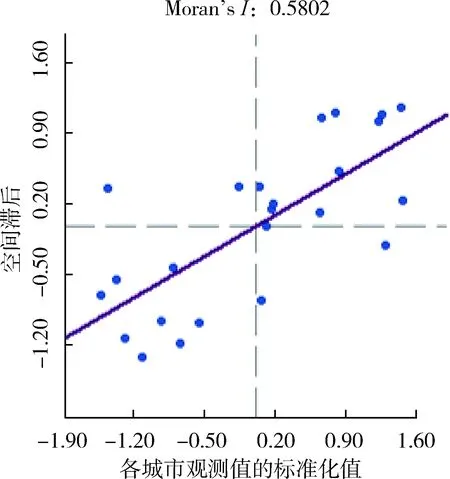
为了更清晰地展示长江三角洲地区26个城市水资源利用效率的空间特征规律，计算局部莫兰指数，在Z检验(5%)的基础上绘制散点图和LISA聚集图，如图3、图4所示。图3中，空间权重中没有邻居的对象已被删除。从图3可以看出，2006年、2009年和2012年落在第一、三象限的城市居多，落在第二、四象限的城市只有5个，表明城市水资源利用效率显著正相关，且关联性较强。而2015年，虽然落在第二象限的城市增加了一个，落入一、三象限的城市依然是大多数，说明城市空间关联效应明显且大多为正的空间联系。

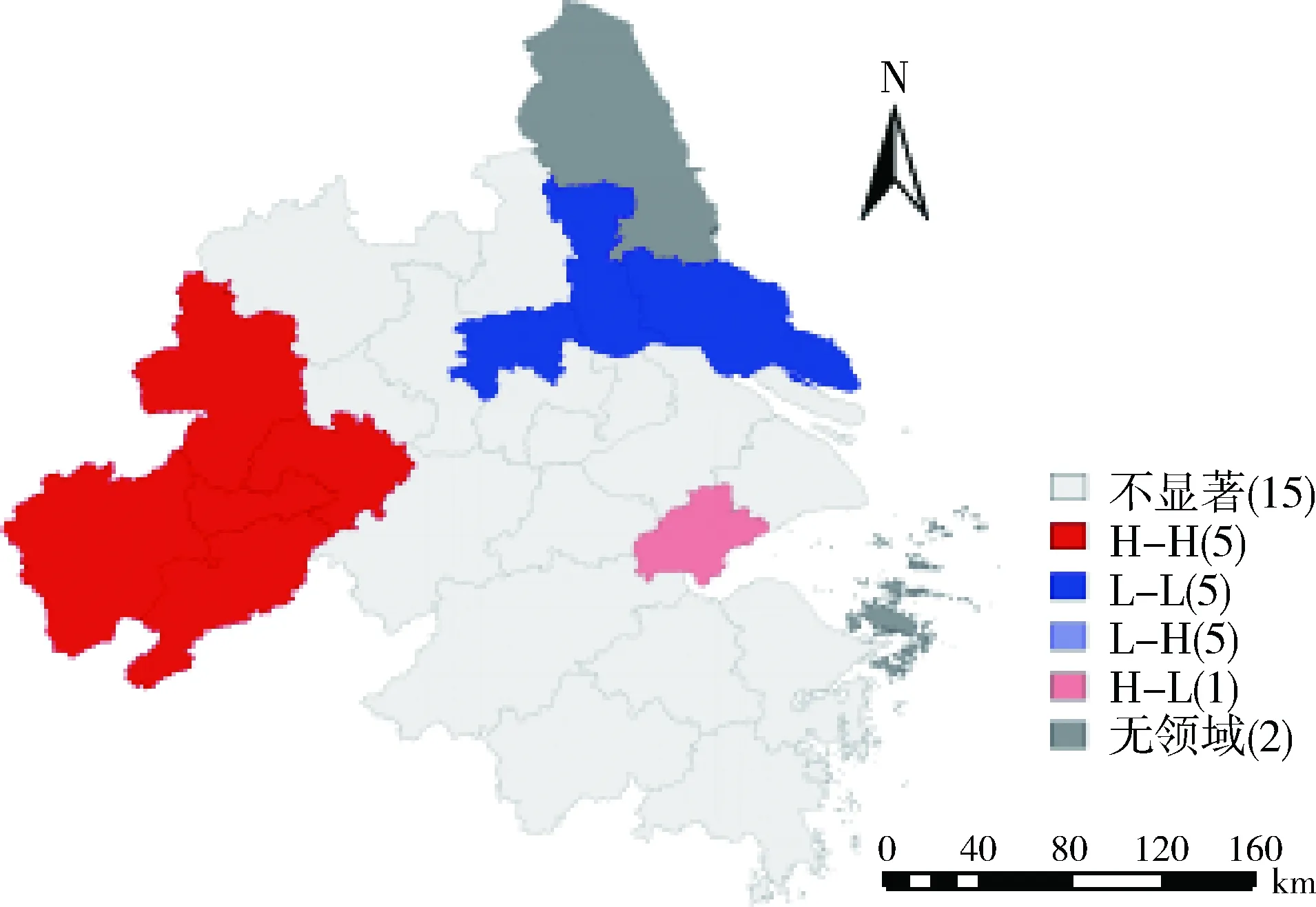
从图4可以看出，去掉两个没有邻居的区域之后，2006年和2009年的LISA聚集图相同，落于 H-H 扩散效应的为安徽省的安庆、池州、铜陵、合肥和芜湖5个城市，说明该地区局部城市存在较强的空间关联和趋同。池州市的水资源利用效率一直很高，另外4个城市经过10年的发展，水资源利用效率也有所改善，这与本文的结论一致。L-L低速发展区域为江苏省的镇江、泰州和南通3个城市，说明该地区局部城市也存在较强的空间关联和趋同。而H-L区域只有浙江省的嘉兴市，该市虽然水资源利用效率水平较高，但未带动周边城市，处于为自己聚集能量的阶段。而2012年和2015年的LISA聚集图相一致，相比于2006年和2009年而言，唯一的变化在于没有落在H-L区域的城市。剩下的15个城市在4个年份都是不显著，说明在长江三角洲地区中，1/2的城市相互之间经济和技术往来较少，系度低，集聚性程度较差，包括经济发展较好的上海、苏州、杭州等城市，表明长江三角洲地区水资源利用效率与经济发展并无很大关联，并没有因为经济水平高而存在较强的空间关联，此结论与杭州经济发展水平与全要素水资源利用效率不成正比的结论一致。

(a) 2006年

(b) 2009年

(c) 2012年

(d) 2015年

4 结 语

a. 从SFA计算的结果来看，2006—2015年，长江三角洲地区26个城市的全要素水资源利用效率一直呈现稳步增长的趋势，但不同的城市之间仍存在一定的差异。对于部分效率较低的城市可以结合当地水质结构与天气情况等，利用技术手段改变水资源利用方法，使其效率得到提高并实现可持续利用，达到人与自然和谐发展的目标。对设备简陋且缺乏资金的企业，政府可以加大投资，帮助其采购一些效益高但耗能低、污染轻的设备，减少其因采购设备而投入过多的生产经营成本，间接为企业环保投入资金从而使企业达到环保标准。

b. 长江三角洲地区水资源利用效率的全局空间自相关分析结果表明：长江三角洲地区水资源利用效率整体来说存在空间自相关性，在空间上呈现聚集特征。长江三角洲地区水资源利用效率的局部空间自相关分析结果表明：落入一、三象限的城市依然是大多数，说明城市空间关联性、溢出效应明显且大多数为正的空间联系。除去2个无邻域不分析的城市外，位于H-H区域的为安徽5个城市，位于L-L区域的为江苏3个城市，剩下的16个城市都是不显著，包括经济发展较好的上海、杭州等，说明在长江三角洲地区，1/2的城市相互之间经济和技术往来较少，联系度低，集聚性程度较差。政府可以牵头绿色转型成功的企业进行经验分享，帮助工艺技术和方法落后且缺乏采购途径的企业，加强与这些企业的交流，从而引进先进的技术，大力发展清洁能源生产，升级绿色工艺。

c. 效率是长江三角洲地区未来水资源管理的重点，从效率的变化情况来看，研究期间长江三角洲地区的水资源利用效率不断提高。但随着经济的快速发展，用水需求将会进一步增加。因此，长江三角洲地区在未来的水资源管理中，应通过提高用水效率，缓解经济发展与用水总量需求同步增长的情况。建立严格的用水管理制度，充分发挥价格杠杆的调节作用，建立合理的用水效率评价体系，以提高水资源利用效率为首要目标。