SCARA机械臂在金针菇搬运生产线中的应用研究
2021-04-16张守丽俞玥
张守丽,俞玥
(1.湖州职业技术学院机电与汽车工程学院,浙江湖州313000;2.江苏科技大学粮食学院,江苏镇江212003)
金针菇生产线,是指在人工提供利用金针菇生长的环境下,采用现在工业化的设备按照标准的工艺流程进行生产[1]。金针菇的搬运装箱作为工业化生产的最后环节,其搬运速度决定了整个生产线的效率。与传统人工搬运相比,机械臂具有生产效率高、耐疲劳、精度高、稳定性好、作业空间小和成本低等优势,大大提高了生产效率,且无人工直接干预实现无菌化搬运装箱。
在金针菇搬运过程中,机械臂需要满足作业空间小、速度快、定位精度高等特点,因此常用的搬运机械手有[2]:码垛机械臂、直角坐标机械臂、Delta 机械臂和SCARA 机械臂等。码垛机械臂是一种串联机械臂,其柔性好、负载能力强,主要用在仓库重物搬运和码垛中。直角坐标机械臂结构简单、运动轨迹也简单,只能在特定的几个方位移动。Delta 机械臂是一种并联机械臂,主要配合图像识别系统实现分拣、抓取和摆放,虽然其运动精度和智能化都很高,但其运动耦合性使其运动分析较为复杂。而SCARA 机械臂是一种串联结构,精度高、运动灵活,在其扇形作业空间内实现任意点移动,特别适合垂直空间内的上下料、拾取、包装和搬运工作。根据金针菇生产具有轻工业性的特点,SCARA 机械臂以其一定承载能力、运动灵活、作业空间小和结构简单的特点被广泛应用其中。
无论什么样的机械臂,在使用过程中都需要对其进行轨迹规划,即描述出机械臂在笛卡尔空间或关节空间的运动曲线,保证其运动过程中速度和加速度无突变,轨迹平滑无冲击,且运转周期最短;李远等[2]提出了改进的S 型曲线对包装机器人进行轨迹规划,提高了运行效率;张程等[3]把机械臂在笛卡尔空间和关节空间的轨迹规划作对比,在满足作业目标的下得到更优的轨迹路径;唐建业等[4]提出了一种改进的多项式插值轨迹规划法,实现时间和冲击综合最优,提高了机器人的工作效率和作业精度;陈学锋[5]基于遗传算法设计了一种轨迹规划方法,改善了码垛机械臂的运动性能,提高其工作效率。本文在现有研究的基础上,对金针菇生产线中SCARA 机械臂进行轨迹规划,得出更加合适的轨迹方程,在满足其稳定性和精度的前提下,提高其工作效率。
1 SCARA 机械臂
1.1 三维模型
本文研究的机械臂结构是根据实际工作要求和目前常见的SCARA 机械臂结构形式设计而成,如图1所示。
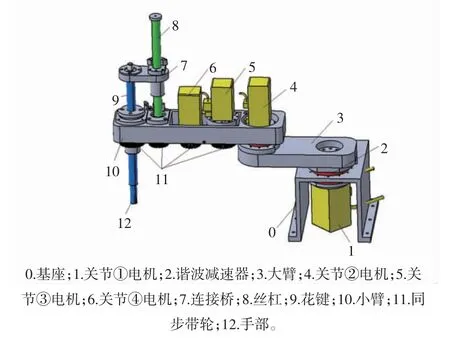
图1 总体结构Fig.1 The overall structure
该机械臂是由4 个运动关节组成的一种水平搬运的机械手臂,主要由基座、大臂、小臂和手部4 个组成部分,其中基座0 与关节①电机相连,分别实现机械臂本体的位置固定和带动大臂3 转动;关节②电机连接大臂3 和小臂10,实现小臂绕大臂转动;关节③电机与丝杠8 通过同步带轮11 传动,实现花键9 上下运动,使手部12 位置调整;关节电机4 与丝杠9 通过同步带轮11 传动,实现花键9 的旋转,使手部12 角度调整,通过4 个关节的配合运动从而可以使搬运的物体放到指定的位置。
1.2 搬运要求
机械臂的工作空间指是小臂和大臂之间的圆环区域,该运动区域保证了机械臂工作空间的多样性和灵活性。根据金针菇搬运要求,其在搬运流水线的运动布局如图2 所示,机械臂的运动范围如图3 所示。

图2 搬运流水线的运动布局图Fig.2 Motion layout of handling line
金针菇从培养瓶中挖出来后,通过生产流水线送到待包装点即图中的金针菇位置,机械臂手部顺次抓起金针菇并将其放置到包装箱内,即完成一次搬运工作,用机械臂可以避免码垛时破损,有利于食品物流发展。

图3 工作范围Fig.3 Working range
2 SCARA 机械臂和机械手运动优化
2.1 SCARA 机械臂运动学分析
运动学分析研究机械臂在工作过程中的运动特性即关节变量随手部位姿的变化情况,不包含其受到的驱动力或力矩,可以分为运动学正解和运动学逆解。
2.1.1 D-H 参数建立
SCARA 机械臂是一种串联结构,可以将个机械臂和关节电机简化以下几何要素和参数,即连杆夹角θ、连杆扭角α、连杆长度L 和两杆距离d[6]。在笛卡尔坐标系中采用第二种坐标系方法,根据结构形式逐级建立如图4 所示的D-H 参数模型和如表1 所示的D-H参数。

图4 机械手坐标系Fig.4 Manipulator coordinate system

表1 D-H 参数汇总Table 1 D-H parameter summary
2.1.2 运动学正解
运动学正解已知关节坐标和相应的速度、加速度求出手部的坐标和相应的速度、加速度,即已知关节变量求手部位姿[7]。根据表1 中的D-H 参数,建立连杆i 和连接杆i+1 的齐次变化矩阵。第二种坐标系下的变换通式如式1 所示。
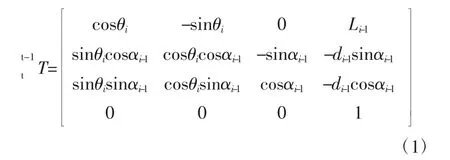
根据表1 和式(1),按照关节坐标系相邻变换原则,即可求得相邻关节的齐次变换矩阵。各相邻连杆齐次变换矩阵依次相乘,即得到机械臂手部坐标系相对于基坐标系的位姿,如式(2)所示:

2.1.3 运动学逆解
运动学逆解是已知手部坐标和相应的速度、加速度,求关节坐标和相应的速度、加速度,即已知手部位姿求关节变量,逆解主要用在关节运动控制和轨迹规划中[7]。对文中SCARA 机械臂来说,其逆解可表示为已知04T 的数值,求解出关节变量θ、a、L 和d 的所有可能解,式(3)可以改写为:

由于采用解析法求解,式(3)得到的解中会有多组可能解,需要根据机械臂结构限制和工作要求选取最合适的一组解,即为要求的关节变量。
2.2 SCARA 机械手的轨迹规划
轨迹规划是指已知机械臂手部的起点和终点,在这个起点和终点的运动过程中有许多条路径,在这些路径中选择一条速度和时间最优的路径,且这条路径要保证机械臂在工作中平稳、无冲击。
关节空间规划法和笛卡尔空间规划法是机械臂轨迹规划中最常用的两种方法[8]。食品生产线中机械臂需要经过路径的特定点,但不考虑整个运动路径问题,因此选用关节空间规划法。关节空间规划法的主要思路就是运用运动学逆解求出机械臂手部经过路径点时所对应的关节变量,在满足约束条件下求出一条光滑连续的多项式轨迹方程,该轨迹方程保证了关节变量在随时间变化过程中的连续性和平滑性。
轨迹规划中三次多项式和五次多项式是关节常用的两种插值函数。三次插值函数保证了关节在运动中位移和速度的连续性,加速度会出现不连续或突变,引起机械臂冲击,但该函数计算量小;五次多项式保证了位移、速度和加速度的连续性和平滑性,避免了机械臂冲击,但该函数计算量大[9]。综合上述两个函数的优缺点,本文选用3-5-3 分段轨迹法,即把路径分为3 段:在起动阶段和终止阶段采用三次插值函数,中间阶段采用五次插值函数。
为了使计算方便,文中引入了无量纲时间变量t∈[0,1],则t 的表达式[5]如下。
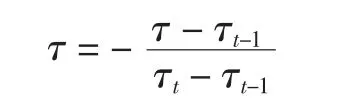
式中,τ∈[τi-1,τi]为运行该段的实际时间,τi-1为第i 段的开始时间,τi为第i 段的结束时间,故机械臂关节的轨迹可用多项式φ(t)来表示。
由于文中机械臂要经过2 个路径点,故该路径被分为3 段,关节采用的3-5-3 多项式轨迹方程如式(4)所示。
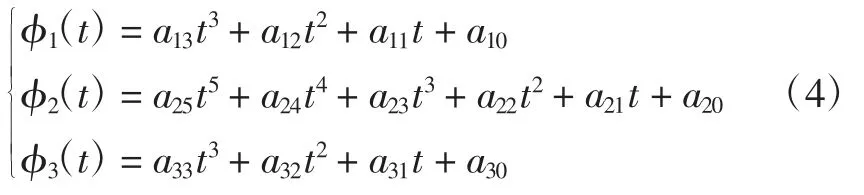
对式(4)中的实际时间τ 分别求一阶和二阶导数,得到角速度和角加速度方程如式(5)所示。
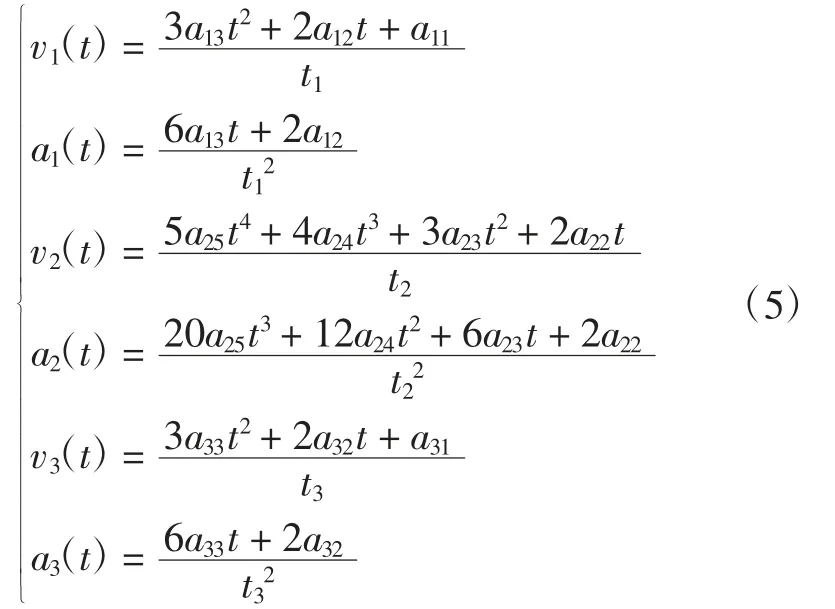
式(5)中共有14 个未知量,需要对应14 个边界约束条件方可求解,路径的起始点的角速度和角加速度均为0,满足约束条件如式(6)所示。

路径点速度和加速度连续的特点,满足约束条件如式(7)所示。

式(6)和式(7)带入式(4)和(5)中,求得各段多项式系数如下。

由式(8)~(10)带入式(4)能够得出各段的轨迹方程。当起始点和路径点位置已知时,由各段时间间隔ti可求得机械臂关节的角度、角速度和角加速度[5]。
2.3 基于遗传算法的时间优化
轨迹优化是指机械臂在路径运动的过程中,找到一条速度和时间均最优的路径。时间最优和能量最优是目前轨迹优化中主流,在实际生产和操作中,时间最优用的最多[10]。本文通过遗传算法对时间进行优化,使式(4)在初定时间变量空间内找到最优时间得到未知系数并确定规轨迹方程,该方程既保证机械臂完成运动且满足速度约束条件。
文中SCARA 共有4 个关节电机且均为旋转运动,其中关节3 和关节4 电机是调整手部位姿,不影响机械臂的运功空间,关节②和关节①是一样的控制方法,故文中仅对关节1 进行优化,其余关节优化方式相同,文中不再陈述。前文中路径分为3 段,使各段时间最优时即整条路径最优,关节1 优化目标函数[11]为:
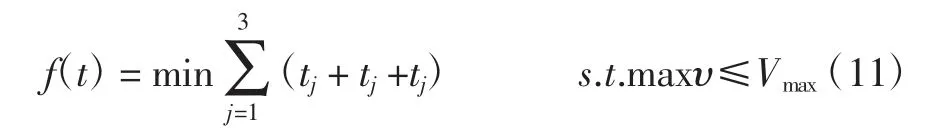
式中:tj为某段所需时间,s;f(t)为优化目标函数;maxυ 为约束条件。
遗传算法对各段路径时间进行优化,优化过程中各基本参数:种群规模取50,交叉概率取0.7,交叉变异概率取0.1,适应度计算取排序法,采用随机抽样。取关节1 的最大角速度约束为55°/s(1 rad=180°/π),路径点坐标见表2。
通过Matlab 编程优化仿真得到最优时间间隔和总时间,优化结果如表3 所示。
经过该时间优化后,仿真描绘出机械臂关节1 的角度、角速度和角加速度曲线如图5 所示。

表2 路径点坐标Table2 Path-point coordinates

表3 时间间隔优化结果Table 3 Time interval optimization results

图5 关节1 曲线Fig.5 working range of joint 1
由图5 结果可知,SCARA 机械臂的关节1 可以准确到规划的路径点,其最大角速度为54.2°/s,在约束的控制范围内。在整个仿真过程中,关节的角度、角速度和角加速度连续且变化平稳,满足机械臂稳定性要求。优化后,机械臂整体运动时间减小39.8%,提高了机械臂的工作效率。
3 结论
(1) 结合金针菇生产线的实际状况,设计出SCARA 机械臂,对其进行运动学分析,通过运动学正解和逆解得到各路径点位姿所对应的各关节变量。
(2)运用3-5-3 分段多项式法对路径点的进行轨迹规划,解决了仅用三次函数的加速度不连续或突变抖动问题,且比仅用五次函数计算量小。
(3)以最大角速度为约束条件,采用遗传算法对各段轨迹时间进行优化。优化后的轨迹曲线不仅满足速度约束和运动平稳性,而且节省39.8%的时间,提高机械臂工作效率。对机械臂的运动控制具有指导意义。
