卫星伪距多路径时空建模研究

王思远， 王 坚， 刘培源

(北京建筑大学测绘与城市空间信息学院，北京 102600)

0 引言

随着全球定位系统(Global Positioning Sys-tem，GPS)技术的高速发展，高精度定位应用需求广泛增加，在灾害监测、建筑健康监测、无人驾驶等领域发挥了重要作用。时至今日，高精度定位信息由原来的cm级精度向mm级精度迈进[1]。卫星通信技术与地面控制部分相结合的创新性想法，提高了农业、工业等民生领域的经济收益，且有力地促进了数字经济的高速发展，极大地推动了导航领域智能化尖端化进程。GPS的最大优点是，在用户有接收器的情况下，可以享受GPS在地球上任何一点提供的导航和定位技术[2]。但是由于受到软件和硬件等多种因素影响，多路径误差仍然是制约GPS技术向更高精度发展的主要误差源。

目前，常用的削弱多路径效应的方法有：Satirapod等[2]基于多路径误差与地球周期相关的特性，利用小波变换的方法分离信号中的多路径误差；Han等[3]提出了利用有限脉冲响应(Finite Impulse Response，FIR)滤波方法进行多路径误差削弱；Bian等[4-5,11]提出了一种基于经验模态分解(Empirical Mode Decomposition，EMD)的算法进行多路径误差的建模和削弱。上述这些方法不同程度地对多路径、日照、环境温度等进行建模，但在信号与噪声的精细分离方面，仍有进一步研究的必要。文献[6-9]中将EMD 去噪法和小波分析法分别应用到一组仿真数据和多路径实测数据当中，通过比较去噪结果，证明了 EMD 去噪法和小波分析法的去噪效果相差不大；但是由于EMD法不用考虑分解层数对数据处理的影响，具有处理数据的通用性，且小波变换缺乏自适应性处理能力，在提取多路径效应模型方面有更大的优势。

本文采用EMD来反映数据本身的特性。在时间轴坐标序列中，通过使用经验模态分解将原始数据层层分解，可以清晰地看出数据每层与每层之间的差异，从而将多路径误差和随机噪声分离；提取多路径误差，构建误差模型，进而代入第二天的观测数据，利用函数模型剔除多路径误差。通过与位置的真实坐标信息进行比较，验证和评价多路径误差模型的精度。

1 多路径效应

多路径效应(图1)是影响全球导航卫星系统(Global Navigation Satellite System，GNSS)数据质量的重要因素之一，这些被反射的信号与直接被接收机接收的信号相互重叠相互干扰，从而产生观测误差。此外，该误差随接收机周围环境及环境性质的不同而变化，因此很难建立一个通用的数学模型来描述它，这也是日常生活中难以削弱多路径效应的原因。根据三维坐标对比分析，在比较常见的实验场景中，多路径效应对长基线测量的影响可以达到m级，对短基线测量的影响可以达到cm级[7]。

图1 多路径效应示意图Fig.1 Mechanism of multipath effect

多路径效应的实时频率与接收机和反射源的距离有着直接关系，多路径误差在主要反射源与接收机距离较远时表现为高频信号，在较近时表现为低频信号。多路径效应主要是由近程反射引起的[8]，当d=20m时，信号功率下降35dB；一般来讲，当主要反射源远离接收机20m以外时应忽略多路径效应，因为多路径效应与接收机所处地理位置和卫星的空间三维位置以及当前GPS时有关[5，13-15]。已知GPS中单颗卫星的运行周期约为12h，因此，对于同一个观测站，周边环境相对稳定的两个相邻日的多径效应具有很强的相关性[10，12，15]，其相关系数为

(1)

式中，rxy(l)为x序列和延迟y历元的y序列的协方差；rxx(0)和ryy(0) 分别为x序列和y序列的方差。

(2)

式中，x(n)和yl(n)分别表示x序列的观测值和y序列的观测值。根据NMEA-0183协议规定可得，当相邻两天的观测数据具有最大强相关性时，第二天的数据应比第一天提前236s。

2 EMD

经验模式中的分解是Huang等[9]提出的自适应信号分解算法，经验模态分解是将复杂信号分解成有限个固有模态函数(Intrinsic Mode Func-tion，IMF)。分解后的IMF分量包含原始信号不同时间尺度的局部特征信号。IMF必须满足以下两个属性：1)端点信号(最大值或者最小值)数目和过零点数目相等或最多相差一个；2)由上包络线组成的局部最大值和由下包络线组成的局部最小值的平均值为0，最终将信号X(t)分解为

(3)

式中，IMFi(t)为IMF算子；rn(t)为残差算子。EMD算法如下：

1)分辨并提取出原数据序列X(t)的所有极大值点和极小值点，将其用三次样条函数分别拟合为原序列的上下包络线；上下包络线的均值为m1，将原数据序列减去m1可得到一个减去低频的新序列h，即h1=X(t)-m1；一般h1不一定是平稳数据序列，为此需对它重复上述过程。如h1的包络均值为m11，则去除该包络平均所代表的低频成分后的数据序列为h11，即h11=h1-m11；重复上述过程，这样就得到第一个本征模函数分量c1，它表示信号数据序列最高频率的成分。

2)用X(t)减去c1，得到一个去掉高频成分的新数据序列r1；对r1再进行上述分解，得到第二个本征模函数分量c2；如此重复直到最后一个数据序列rn不可被分解，此时，rn代表数据序列X(t)的趋势或均值。在算法中的极值点是指一阶导数为零的点。

3)理论上，X(t)可以表示为N个IMF分量以及一个残余分量。给出的筛选过程结束标准是一种类似于柯西收敛准则的理论标准。

3 GPS静态观测数据分析

3.1 实验场景及分析数据

为了研究GPS静态观测实验中的多路径效应，实验场景选取北京建筑大学F教学楼前空地旁东，四周开阔，无明显遮挡物，且场地周围基本无车辆经过。设立2×3+1的GPS静态接收机阵列(如图2 所示)，横向接收机彼此间隔1.5m，纵向彼此间隔2m，接收机统一设置高度为1.5m，保持7台接收机在同一高度线上(6台实验，1台检核)。

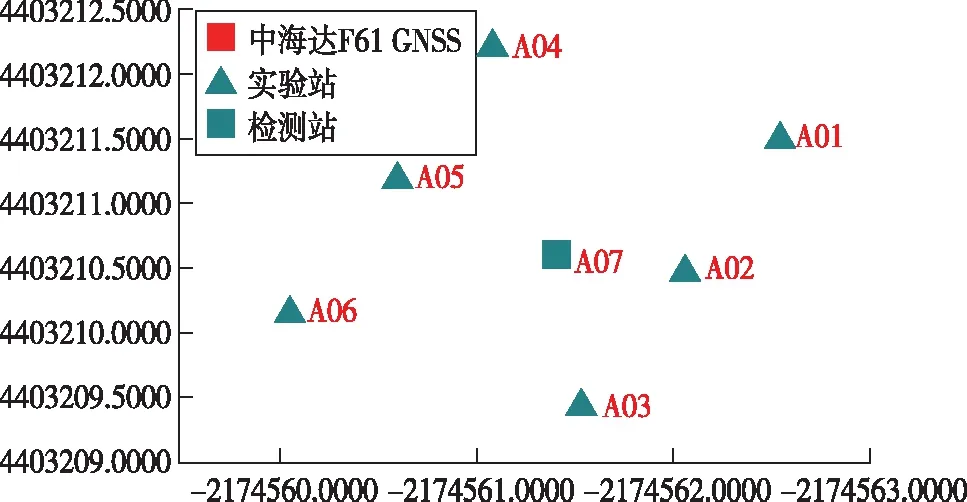
图2 接收机阵列图Fig.2 Receiver array coordinates

因为本文采取的是短基线测量实验方案，所以可以利用差分载波相位技术消除卫星与接收机钟差，大大削弱了对流层和电离层误差以及卫星轨道误差的影响。然而由于多路径误差和观测时产生的白噪声无法用技术手段消除，可以认为坐标残差序列由系统性的多路径误差和随机噪声组成。利用解算软件可以得到原始数据的三维坐标序列，由于主要遮挡物在E方向，所以主要研究E方向的多路径效应。通过图3可以看出，相邻两天同一观测时段三维坐标的大致走势基本相同。通过计算得出第二天的坐标序列相较第一天提前了大约4min(240s)，且E方向(主要遮挡物方向)的坐标序列的相关性系数最大值达到0.83，说明相邻两天同时段的数据具有强相关性。

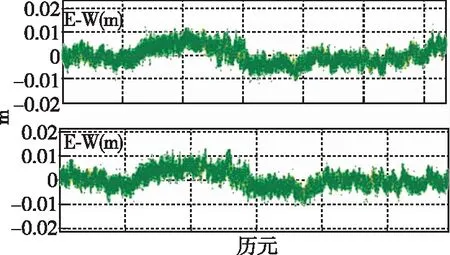
图3 相邻两天E方向的坐标序列Fig.3 A sequence of coordinates in the E direction of two adjacent days

由于GPS静态观测数据的误差主要由多路径效应和白噪声引起，其中多路径误差在反射源距离接收机阵列较近时，其信号具有低频特性，而白噪声具有高频特性。

因此，利用这一特点可以使用EMD对原始数据进行多层次分解，并提取其中的多路径误差数据。本文从E方向(遮挡物和主要反射源方向)进行分析，对第一天的GPS观测数据进行经验模态分解，将观测数据共分为十层，如图4所示。

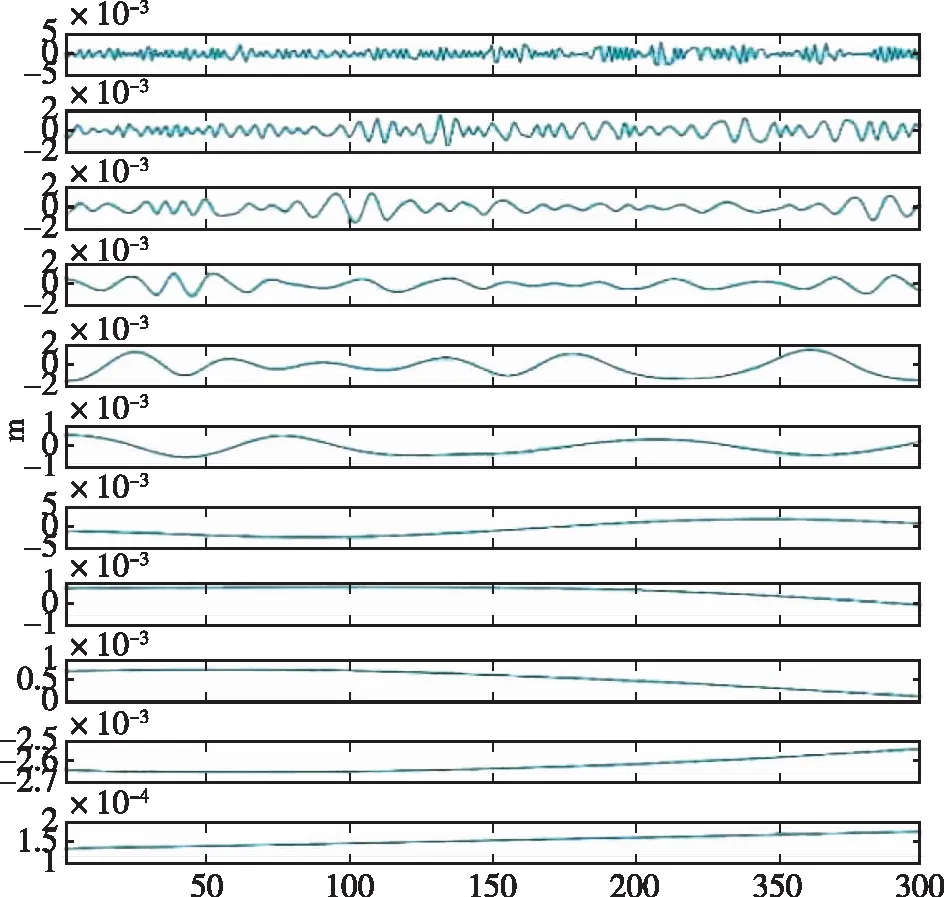
图4 E方向坐标EMD分解效果图Fig.4 EMD decomposition effect of coordinates in E direction

本文从E方向(遮挡物和主要反射源方向)进行分析，经过观察可以得出从第三层开始出现明显偏离零值的趋势，所以分解尺度取为3(dn=3)，得到3个模量与7个趋势项。原始数据被分为了十层，其中前三层为高频的白噪声，后七层为低频的多路径误差。这样将多路径误差和噪声误差加以区分，并分别提取它们的误差数据,如图5所示。

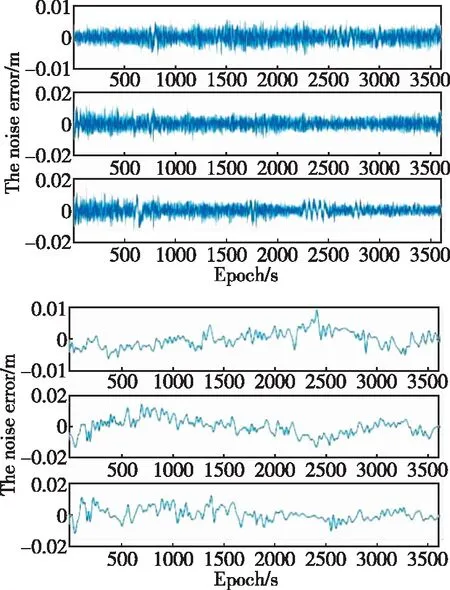
图5 提取的噪声误差和多路径误差Fig.5 Extracted noise error and multipath error

3.2 误差模型拟合

通过MATLAB自编程序进行多项式拟合，然后利用程序拟合二次曲面的参数值并绘制拟合曲面图像。多项式拟合的流程如下，先对平面坐标数据进行重心化，然后利用公共点数据运用最小二乘求解参数。

通过多项式拟合，得到接收机阵列的拟合图像，如图6所示。可以得到在三维空间内接收机的大致位置，虽然尽量使得7台接收机在同一高度，但是通过拟合图像可以看出，还是在一定程度上有高低不平，存在一定的高差，这也造成了一部分观测误差。通过拟合模型可以轻松地知道，在阵列内任意一点的三维坐标，只需要输入他们的平面坐标，即可通过拟合模型得到它们的三维坐标。

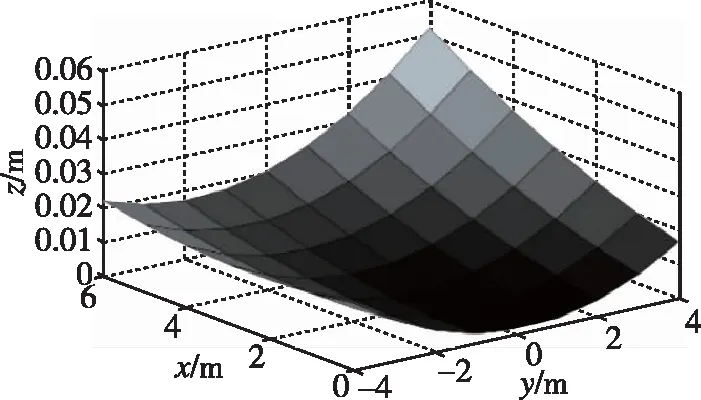
图6 接收机阵列拟合图像Fig.6 Receiver array fitting image

通过对第二天观测数据进行剔除自身多路径误差和利用第一天多路径模型对第二天数据进行后处理两种方法，削弱多路径效应，得到剔除多路径误差的坐标序列如图7和图8所示。将检核站的

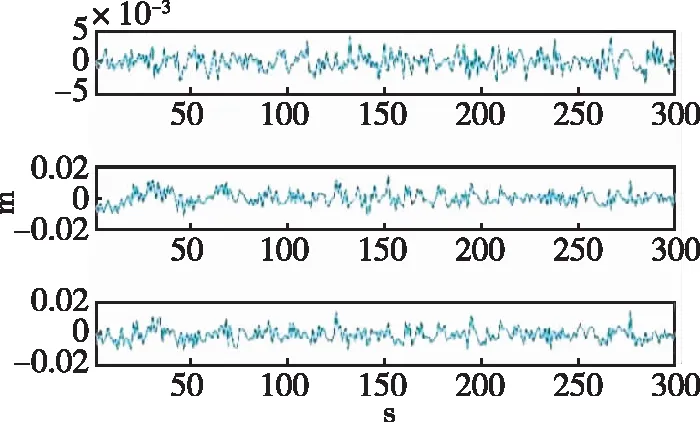
图7 剔除自身多路径误差的三维坐标序列Fig.7 3D coordinates sequence excluding its own multipath error

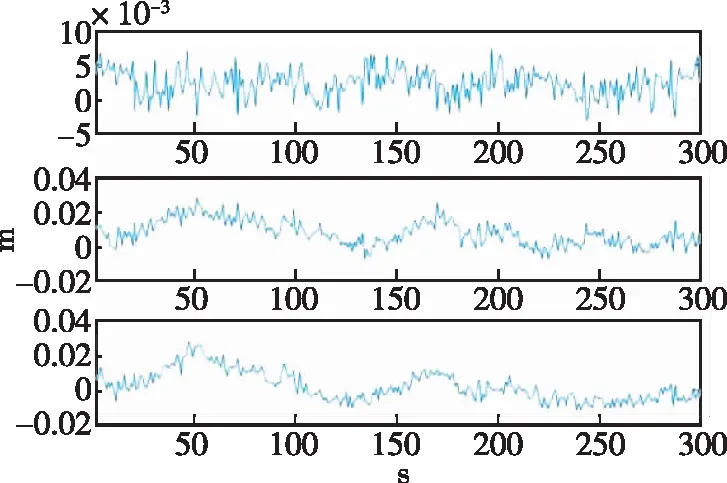
图8 剔除理论相关系数最大多路径效应后的坐标序列Fig.8 Coordinates sequence after eliminating the maximum path effect of theoretical correlation coefficient

坐标序列代入误差模型中，通过与真实坐标值进行对比，可以看出实验方法的有效程度。

3.3 误差分析

通过对比图7和图8可得，剔除多路径误差后的数据序列都得到了明显的改正，多路径效应在很大程度上得到了修正，一定程度上证明了理论方法的可行性。同时，因为主要反射源处于接收机阵列的东方向，所以本实验中通过实验流程对E方向去除多路径误差后，得到的三维坐标序列改善效果最明显;而N方向和H方向虽然也有不同程度上的改正，但是他们的幅度较低，基本可认为这两个方向受多路径效应的影响较小。

通过对剔除理论相关系数最大多路径效应后的坐标序列和剔除自身多路径误差的三维坐标序列进行对比可以看出，运用本文理论使用多路径误差模型提取多路径误差的工作卓有成效，得到的实际多路径误差与通过模型拟合所得的多路径误差相差不大，基本可以在类似本文实验环境下使用该理论方法进行多路径误差修正工作。

本实验流程中虽然存在误差，但误差范围基本控制在mm级范围内。由此进行S07接收机的测试工作，将检核点接收机的观测数据分为12个时段代入12个误差模型中，得到他们的坐标拟合值，并与真实值进行对比，可获得如下的实验结论：在小范围区域内，只要将需要获取三维坐标值的任意一点观测坐标代入当前时段的误差模型中，经过误差模型改正，都能获得更接近真值的模拟坐标数据。实验过程中，采集的原始数据中多路径效应较为明显，多路径误差达到cm级，经过实验流程处理过后，多路径效应得到了大幅度的减弱，证明了多路径误差得到了有效的剔除。经过计算，如表1所示，多路径误差的削弱程度一般能到35%以上，精度得到了明显提高，通过对误差模型改正后的三维坐标和剔除自身多路径误差后得到的坐标与接收机阵列真实坐标进行对比，证明了本实验所描述的流程确实有效。

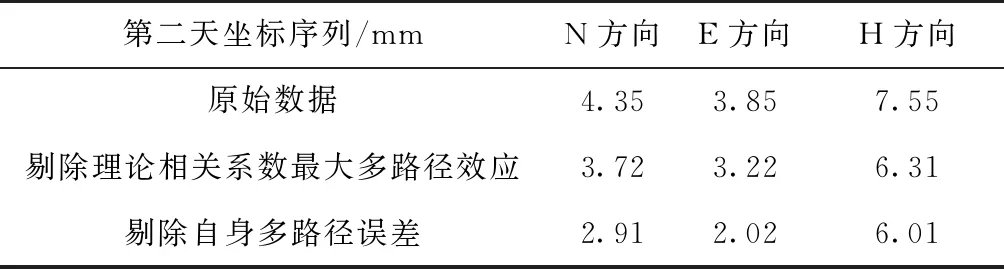
表1 多路径误差去除前后标准差对比

4 结论

1)随着GPS定位技术对精度和准度要求的日益增高，如何处理和削弱多路径效应成为了重要工作。本文利用多路径误差的产生机理和频率特性，以及同一观测站相同时段数据间的强相关性，基于EMD方法对三维坐标序列进行处理，利用提取的多路径误差进行函数拟合并建立函数模型。通过多路径误差函数模型对第二天的原始数据进行后处理，得到提取误差的数据与原始数据相比，主要反射源E方向的坐标精度明显提高。经过试验论证，接收机观测序列中的多路径误差得到了大幅度削弱，受到多路径效应影响的主要观测方向修复程度可达35%以上。在适宜的环境下使用该方法，可以有效减少多路径效应对GPS定位结果的影响，从而使定位精度有望向亚mm级迈进。

2)对于环境比较恶劣的情况，接收机接收的数据稳定性较差，由于函数模型具有非普适性，还需要进一步研究，可能与运用函数模型方法削弱多路径效应的效果相比，改善周围环境，增加阻流环、直径抑制器等装置也许会获得更好的效果。

3)如果周围接收机环境较好，单一反射源或者周围视野开阔，在运用本文方法处理的同时，还可以通过选择清晨和傍晚两个时段的数据来减弱多路径效应，因为9～15点时间段的温度较高，容易引起大气层折射现象增大、信号强度减弱、坐标序列稳定性降低等负面效果；还可以通过提高接收机高度截止角来尽量避免信号传输较弱的卫星。