基于热磁耦合分析的高性能磁屏蔽系统设计

2021-04-16张梦诗杨功流段利红

导航定位与授时 2021年2期

张梦诗，杨功流，全伟，段利红，刘峰

(1.北京航空航天大学仪器科学与光电工程学院，北京 100191；2.北京航空航天大学前沿科学技术创新研究院，北京 100191； 3.北京量子信息科学研究院，北京 100193)

0 引言

随着量子力学、现代光学及原子操控技术的不断发展，以原子为敏感介质的量子技术得到了快速发展，以此为基础研制的量子精密测量仪器形成了对相关领域内传统仪器最有力的冲击。利用原子超精细能级结构特性研制成功的原子钟、基于原子核磁共振特性的核磁共振分析仪和磁强计，以及基于原子干涉特性的原子重力仪等[1-3]不断突破传统测量极限，已成为各自领域内精度最高的测量仪器。其中基于原子自旋在惯性空间中的定轴特性研制的原子自旋惯性测量装置[4]，其理论精度仅与量子噪声相关，不受其他干扰，可实现完全无阻尼的转动测量，有望成为新一代的惯性测量仪表。该装置是以无自旋交换弛豫(Spin-Exchange-Relaxation-Free，SERF)状态的保持为前提的[5]，为了实现此目标，就必须通过核自旋磁场自补偿以隔绝外界磁场的变化，且在装有碱金属原子的气室外增加一个加热烤箱，以保证原子始终处于SERF状态所要求的温度范围内[6-7]。原子自旋SERF态的实现对环境磁场也有着极为苛刻的要求，为了避免环境磁场对原子自旋定轴性的扰动作用，需要将其充分隔离。目前，隔离磁场干扰最常用的方法是使用由高磁导率软磁材料制成的磁屏蔽体，因此本系统由多个一端带盖的圆柱体形磁屏蔽筒组成，以实现隔离磁场干扰的目的[8]。

不同于原子钟等磁屏蔽系统的设计，原子惯性测量装置磁屏蔽系统的磁屏蔽效能极易受温度的影响[9]。一方面，受内部热源的影响，磁屏蔽系统结构存在较大的温度差，而磁屏蔽材料的磁导率受温度影响，导致系统各部分的磁导率不均匀，从而影响了磁屏蔽效能，且可能使内部产生磁场梯度。另一方面，外界环境磁场和温度场发生变化时，会引起磁屏蔽系统内部的剩余磁场波动，从而影响惯性测量装置的长期稳定性。在系统工作状态下，由于条件的限制，难以实时测量内部的磁场变化，仅能通过输出信号获得原子气室内的磁场变化。而采用仿真软件对其进行热磁耦合有限元理论分析，涵盖了经典的传热学理论和电磁场理论，可以解决磁场和温度场共同作用的问题，从而获得系统内部的磁场分布[10]。

热磁耦合理论专门研究电磁场和温度场的耦合，即两场间的相互作用、相互影响问题。M. C. Song等[11]采用等效电路模型法对重型船用曲轴的感应加热并进行了热磁有限元分析，预测了不同尺寸工件感应加热的温度分布。G. Zhang等[12]提出了一种三维磁通切换电机的轴向分段磁热耦合场模型，该模型考虑了磁通密度、铁损和轴向温度分布的变化，与二维耦合场模型相比结果更准确。由于涉及电磁场与温度场的相互作用与影响，通常表现出强非线性和强耦合性特征，这不论是在理论模型的建立，还是在问题的定量、定性分析上均有相当大的难度。

本文基于COMSOL的热分析和热磁耦合有限元分析功能，应用传热学理论和电磁场理论，对原子自旋惯性测量装置的磁屏蔽系统进行了热磁耦合仿真分析。这对于全面分析系统结构设计是否合理以及材料的选择是否满足要求具有指导作用，且为高性能磁屏蔽系统的设计提供了重要依据。

1 热磁耦合理论

在热磁耦合问题的定量研究方面，通过先分别对各单独的磁场和温度场进行线性或非线性有限元分析，再对场与场间的相互耦合效应运用非线性迭代算法进行处理的方法，建立了能够定量描述这一多场耦合复杂系统的非线性有限元分析模型。

静态磁场屏蔽计算公式如下:单层圆柱形磁屏蔽筒的径向磁屏蔽系数为[13]

(1)

式中，μr为相对磁导率；d为磁屏蔽材料厚度；D为屏蔽筒直径。

单层圆柱形磁屏蔽筒的轴向磁屏蔽系数为[14]

(2)

式中，a=L/R，L为磁屏蔽筒长度，R为磁屏蔽筒半径，K为

(3)

式中，α和β可以分别通过测量圆柱端和侧壁的标准磁通量分布来确定，通常取α=0.85±0.03，β=1.83±0.06。

在单层磁屏蔽筒轴向屏蔽系数的基础上，可推导出多层圆柱形磁屏蔽桶的总磁屏蔽系数模型如式(4)和式(5)所示[15]。

对于n层磁屏蔽罩有

(4)

(5)

可以发现,在磁屏蔽筒结构尺寸一定的条件下，磁屏蔽效能仅与材料磁导率有关。受系统内部热源的影响，导致结构体存在较大温度差，而软磁材料的磁导率随温度变化，使得结构体各部分的磁屏蔽效能不同，且可能产生磁场梯度。上述模型无法描述这种现象，因此需构建新的磁屏蔽效能与温度相关的模型。

采用热磁耦合场的通用公式[10]

(6)

式中，GA是矢量磁势方程，A是矢量磁势，T′是矢量磁势方程中与温度T有关的项；GT是温度场控制方程，T是温度，A′是温度场控制方程中与A有关的项。

相应的数学表达模型表示为

(7)

式中，L为长度；Vs为电压；μr为磁导率；λ为导热系数；ρ为密度；c为比热；σ为电导率。其中电导率与磁导率均与温度相关。公式表明热源受到焦耳损失的限制。

系统中温度影响材料的磁导率从而影响磁场计算，是温度场与磁场的单向耦合。因此，根据热磁耦合理论，系统的求解过程如图1所示。

图1 热磁耦合求解Fig.1 Thermomagnetic coupling solution

第一步是获取磁屏蔽系统模型的稳态热分析结果；第二步根据磁性能参数随温度的变化情况，及时更新材料的电导率σ和相对磁导率μr，其中本实验不考虑电导率的影响，即把获得的磁导率随温度变化的模型代入其中；再计算下阶段的磁场参数，累次迭代运算，直到磁场和温度场均处于稳定状态为止。

2 磁屏蔽系统的稳态热分析

根据热磁理论分析，在进行系统热磁耦合分析前，应完成磁屏蔽系统的传热学分析，通过离散化计算获得系统结构的温度场数据。由于系统热源设计中有精度为5mK的温控系统，加热温度较为恒定，因此采用稳态热分析方法进行分析与计算。

2.1 磁屏蔽系统的组成

使用三维建模软件完成对磁屏蔽系统的结构建模，如图2所示。

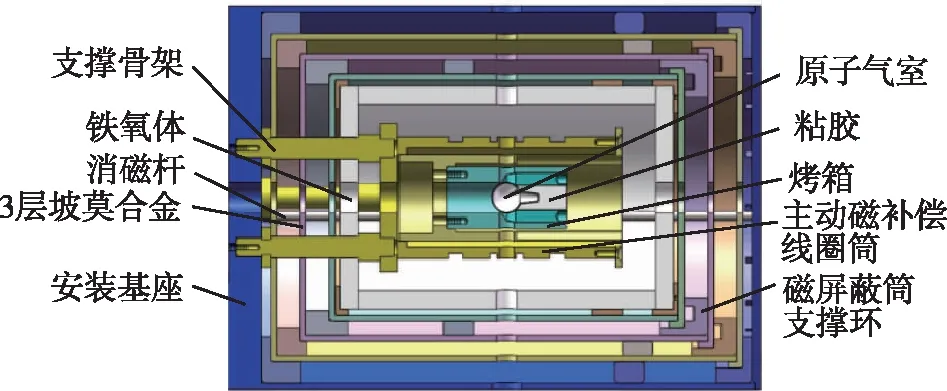
图2 磁屏蔽系统结构Fig.2 Magnetic shielding system structure

由内而外，首先是球形石英玻璃原子气室，通过粘胶被固定于圆柱形氮化硼烤箱的中心处，加热膜片环贴于烤箱的外表面，对原子气室进行稳定加热；再往外分别是主动磁补偿线圈筒、支撑骨架、锰锌铁氧体磁屏蔽筒、钛合金消磁杆、3层坡莫合金磁屏蔽筒，以及最外层的安装基座。磁屏蔽筒的相关尺寸如表1所示。

表1 磁屏蔽筒尺寸

2.2 加热磁屏蔽系统的传热过程分析

根据系统设计，系统内部热源有两处，分别是粘于烤箱表面的电阻丝加热膜片和主动磁屏蔽线圈。与加热膜片的加热功率相比，主动磁屏蔽线圈的发热功率极小，仿真时可忽略不计，因此内部发热源可只考虑电阻丝加热膜片的发热功率。

系统传热主要有两个方向，一方面电阻丝加热膜片通过热传导将热量传递给烤箱，烤箱再通过热辐射和热传导将热量传递给原子气室，实现原子气室加热的目的；另一方面，加热膜片对外有热辐射，同时烤箱可将热量通过热传导的方式传递给支撑线圈骨架，再通过传导和辐射将热量依次传递给主动磁屏蔽线圈组件、铁氧体和磁屏蔽筒等，最外层安装基座对外自然环境对流散热。根据上述分析，绘制磁屏蔽系统的传热过程，如图3所示。

图3 磁屏蔽系统传热过程Fig.3 Heat transfer of magnetic shielding system

2.3 磁屏蔽系统的稳态热仿真分析

在仿真中，如果对系统所有组件都详细建模，网格划分极为细致，会耗费大量的计算时间，因此需对模型进行简化。首先略去倒角、安装定位孔、螺纹、螺栓、螺母、圆角等不影响热路模型的局部细节和连接件；同时由于仿真中不涉及原子气室的热设计，因此可以省去内部原子气室和粘胶。最终建立的简化几何模型，如图4所示。

图4 仿真简化模型Fig.4 Simplified simulation model

将简化后的模型导入COMSOL平台中，设置如下的假设和解析条件：

1)磁屏蔽系统在工作过程中平稳运行，内部加热膜片加热稳定，产生的热通量保持恒定；

2)假定加热膜片的温度与烤箱的温差太小，可忽略不计，经过实验测得加热膜片的加热功率为30W；

3)磁屏蔽筒与外界环境的对流换热系数设置为系统默认5W/(m2·℃)，环境温度25℃；

4)设置线圈支撑外表面对磁屏蔽筒和各层磁屏蔽筒间的辐射，实验测得辐射率为0.7；

5)设置烤箱外表面与线圈支撑骨架之间的辐射，实验测得烤箱表面辐射率为0.9，线圈支撑辐射率为0.7。

同时还需要设定实验中所采用的相关材料的热性能参数，如表2所示。

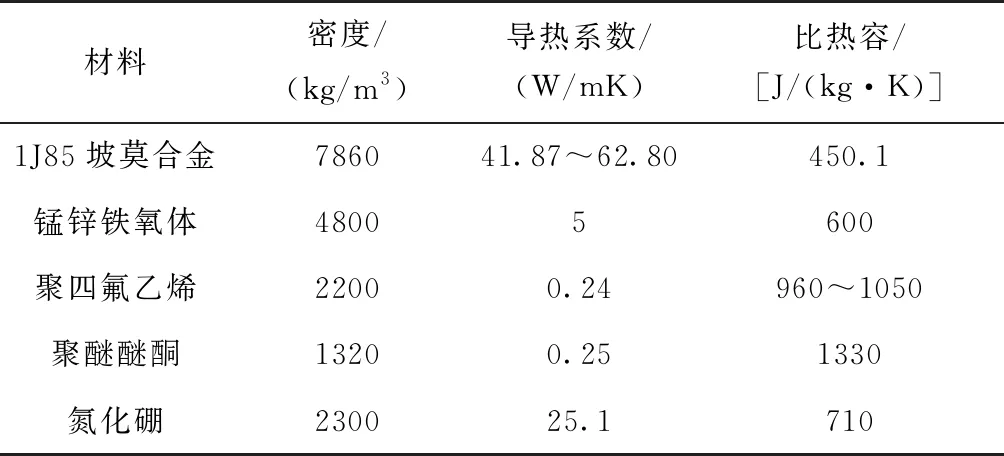
表2 材料热性能参数

在仿真过程中，材料热学参数的误差、热辐射率的设定以及对流换热系数的设定是仿真结果与实际结果产生误差的主要原因。因此，在后续仿真试验中，需保证相关参数符合实际，且设置的边界条件始终保持一致。

利用COMSOL固体和流体传热模块以及表面对表面辐射模块，耦合计算获得稳态热仿真结果，如图5所示。

图5 稳态热仿真结果Fig.5 Steady-state thermal simulation results

从仿真结果发现，磁屏蔽系统结构体间存在较大的温度差，其具体温度变化范围如表3所示。

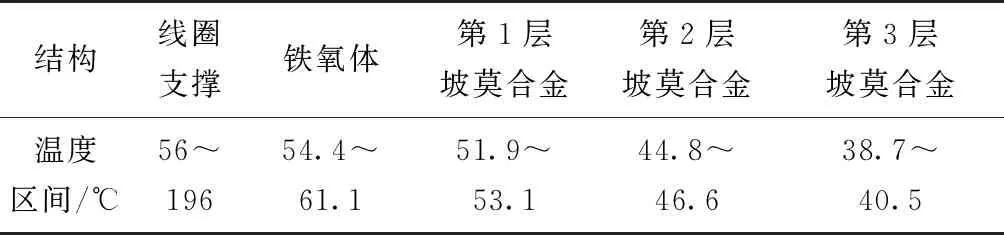
表3 系统结构温度范围

结论：可以发现，各屏蔽筒的温度较高，远高于室温，而且存在较大的温度梯度，尤其是铁氧体层，原因是其导热系数较小，同时结构非完全对称，使得靠近线圈支撑处的温度更高。

3 系统热磁耦合仿真分析

本次实验主要分析温度对系统内部磁场的影响，通过实验获得系统所用的磁屏蔽材料磁性能随温度变化的数值，利用COMSOL的热磁耦合分析模块完成数值计算。

3.1 获取磁屏蔽材料的磁性能参数

根据国标软磁材料磁导率测量方法，采用单线圈法测量标准环形样品的磁导率随温度变化情况。实验装置如图6所示，外部3层坡莫合金屏蔽外界磁场干扰，烤箱以及热电偶保证样品环的测试温度恒定，LCR阻抗分析仪获得电感[16]。

图6 磁导率测试原理图Fig.6 Principle diagram of permeability test

测试方法：在一定温度条件下，在样品环上均匀绕上测试线圈，采用阻抗分析仪测量样品的自感量L和含样品线圈的损耗电阻R，根据公式计算获得其磁导率，起始磁导率计算公式为

(8)

式中，μi为起始磁导率；N为绕阻匝数；L为电感，H；D为样品外径，mm；d为样品内径，mm；h为样品高度，mm。标准环形样品尺寸外径25mm，内径15mm，高度7.5mm。

通过实验获得所采用的软磁材料的磁性能参数随温度变化数值，再通过最小二乘线性拟合获得材料相对磁导率随温度变化关系式，其中锰锌铁氧体的相对磁导率为μr=36.222T+1081.7，坡莫合金1J85的相对磁导率为μr=114.3T+30310。

3.2 热磁耦合有限元仿真

利用COMSOL软件建模，4层磁屏蔽筒一端为端盖，且端盖轴向及磁屏蔽筒中心径向均开有通光孔及定位安装孔，外部由一对亥姆霍兹线圈产生均匀磁场来模拟地磁场环境(地磁场强度约为50000nT)，模拟模型如图7所示。

(a)磁屏蔽系统仿真模型 (b)亥姆霍兹线圈模拟地磁场图7 磁屏蔽系统及亥姆霍兹线圈的仿真模型Fig.7 Simulation models of magnetic shielding system and Helmholtz coil

利用COMSOL的温度耦合模块，将稳态热仿真的离散化计算结果导入磁场分析模块。将获得的磁性能参数随温度变化关系式代入稳态热仿真结果，以解决磁场问题，累次迭代，最终磁场及温度场均稳定，获得图8(a)所示结果；同时设置不考虑温度场仿真作为对照组，即设定材料磁性能参数恒定，采用的相对磁导率参数分别为铁氧体3000，坡莫合金30000，其仿真结果如图8(b)所示。

(a)考虑温度场

(b)未考虑温度场图8 铁氧体层内部的剩余磁场仿真Fig.8 Simulation of residual magnetic field in ferrite layer

选取中心10mm均匀区磁场数据进行分析，分别绘制轴向和径向的剩磁变化，其结果如图9所示。

结论：稳定加热条件下，结构的温度差对内部均匀区10mm内的磁场梯度影响较小,可以忽略。

利用式(4)和式(5)计算该结构尺寸下磁屏蔽系统的屏蔽效能以及剩余磁场大小，并记录仿真结果，如表4所示。

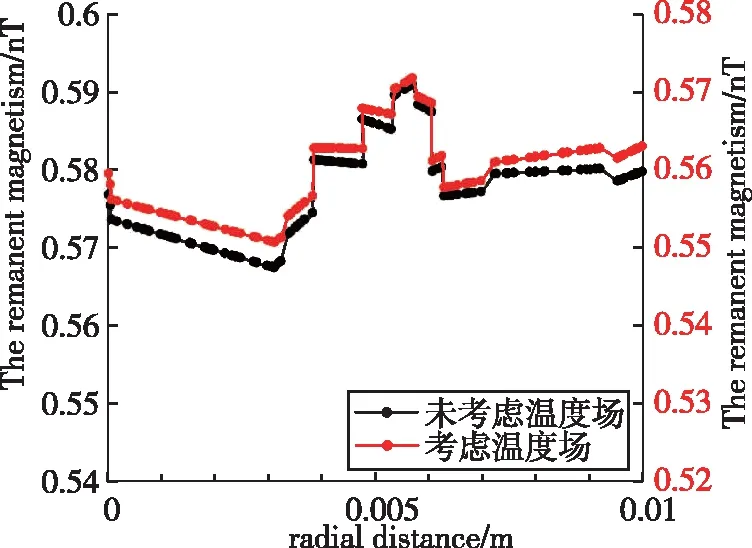
(a)径向剩磁变化

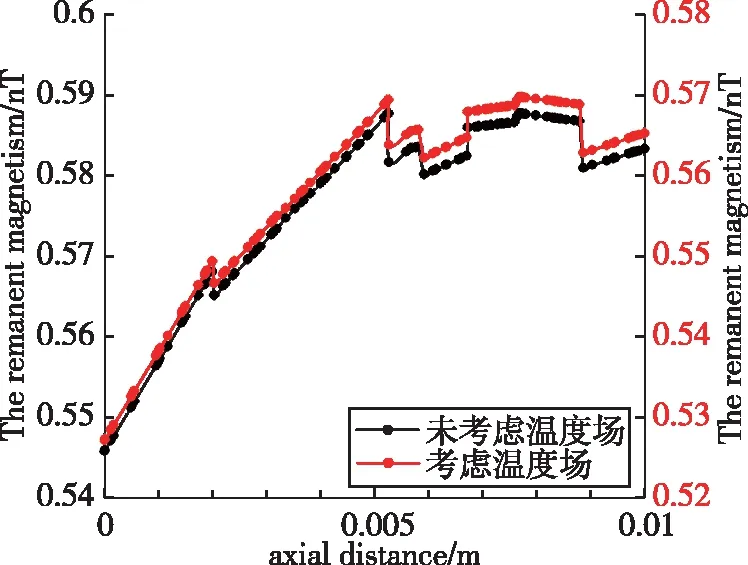
(b)轴向剩磁变化图9 内部均匀区磁场仿真结果Fig.9 Magnetic field simulation results of internal uniform region

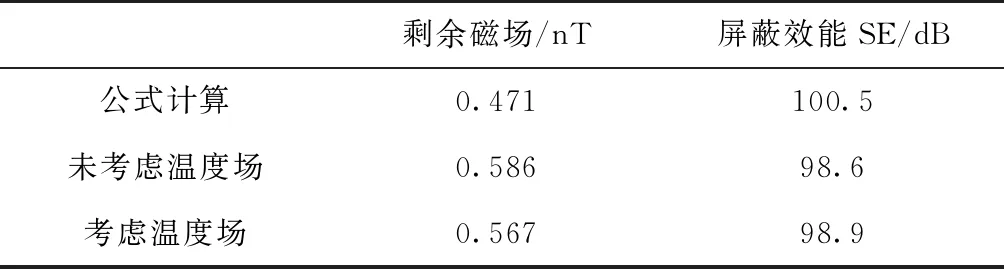
剩余磁场/nT屏蔽效能SE/dB公式计算0.471100.5未考虑温度场0.58698.6考虑温度场0.56798.9

结论：考虑温度场影响后，磁屏蔽系统的内部剩磁与数值计算结果相差0.09nT。其原因是有限元计算结果综合考虑了开孔和温度等影响，更接近实际结果。因此，在计算磁屏蔽效能时，如果有温度场的影响，计算公式需要修正。

4 基于热磁耦合模型的磁屏蔽材料优化设计

磁屏蔽材料磁导率受温度影响同样会影响装置的正常工作，当外界环境磁场和温度发生变化时，磁屏蔽系统内部剩磁波动，从而影响惯性测量装置的零偏稳定性。系统长时间工作的情况下，外部环境温度会不断变化，材料磁导率随之变化，导致内部磁场波动和系统输出波动，造成系统长期稳定性差。

4.1 方案设计

为保证磁屏蔽系统的温度稳定性，对磁屏蔽系统材料进行优化设计，拟采用图10所示设计方案。外部2层采用高温度稳定性的改进坡莫合金材料，对外界环境温度波动不敏感，使磁导率保持相对稳定；中间层采用1J85坡莫合金材料，高磁导率大幅降低了外界磁场；最内层采用锰锌铁氧体材料，产生的磁滞噪声小,对惯性测量装置的输出影响小。

图10 磁屏蔽系统材料优化设计Fig.10 Material optimization design of magnetic shielding system

钢铁研究总院是金属新材料的重要研发基地，是我国金属新材料及制品生产的领军企业。根据需求定制了一种温度稳定性好的坡莫合金材料。通过改变材料配比、加工工艺和热处理工艺等手段对原有1J85材料进行改进，获得了一种适用于全温度范围的磁屏蔽材料，并用此材料设计了新的磁屏蔽筒，实验测得其相对磁导率为μr=16.65T+9475。

4.2 仿真计算

基于建立的热磁耦合分析模型，根据设计方案在仿真时改变外层磁屏蔽筒的磁性能参数，即分别设置坡莫合金相对磁导率低温度稳定性为μi=114.3T+30310和高温度稳定性为μi=16.65T+9475。在磁屏蔽系统的原子气室中心位置设置测量点O，通过改变环境温度(25℃±0.5℃)，每次改变0.1℃并获取该处剩磁结果，仿真结果如表5所示，绘制成折线图如图11所示。

表5 变室温下采用不同温度稳定性的内部剩磁仿真结果

图11 变室温下采用不同温度稳定性的内部剩磁仿真结果Fig.11 Simulation results of internal remanence under different temperature stability obtained at variable room temperature

结论：1)随着外部环境温度变化，其内部剩磁发生波动，采用高温度稳定性材料，剩磁温变率由0.008nT/℃下降至0.001nT/℃，因此证明了采用高温度稳定性材料能有效改善系统温度稳定性；2)采用高稳定性材料后，内部剩磁增大了约1.5nT，其原因是相同结构温度下，采用高温度稳定性材料的磁屏蔽系统的磁导率较低，从而导致屏蔽效能减小。