基于Voronoi图和蚁群算法的无人机航迹规划

2021-04-16王钦禾尹永鑫邹宇翔

导航定位与授时 2021年2期

王钦禾，尹永鑫，戴丽，邹宇翔

(1.中国航天空气动力技术研究院彩虹无人机，北京 100074；2. 国防科技大学文理学院，长沙 410073)

0 引言

与有人机相比，无人机(Unmanned Aerial Vehicle, UAV)具有零人员伤亡、持续作战能力强、全寿命周期成本低，以及在尺寸、速度和机动性等方面的特有优势[1-2]。无人机凭借这些优势，广泛应用于军用和民用领域，其在战场中的作用也越来越被重视。如何提高无人机任务执行能力，成为当下研究的热点。而无人机航迹规划是提高复杂任务环境下平台生存性和完成任务有效性的关键技术之一。因此，研究无人机航迹规划技术，为其找到一条从起点到终点的最优航迹，能够有效保障无人机的飞行安全，提高任务的执行效率，减少不必要的损失[3]。

航迹规划方法按照几何学的观点，可以分为基于栅格和基于图形的算法。基于栅格的航迹规划算法，利用栅格法对任务环境进行建模，优点是精度高、兼容性强，但是数据量大，对机载计算机的计算性能要求高。基于Voronoi图的无人机航迹规划方法，凭借其任务环境模型简洁实用和计算快速等特点，一直是目前比较常用和有效的方法[4-6]。常规 Voronoi 图构图简单，只能用于等威胁体的航迹规划，对实际战场环境的建模有较大的局限性。文献[7-8]提出了基于Voronoi图的新的建模思路，对Voronoi图进行了改进，改进后的Voronoi图更贴近现实情况，更能反映出不同威胁源对无人机威胁的差异性。在Voronoi图的基础上进行航迹规划的算法，主要包括：Dijkstra算法[9]、遗传算法[10]、蚁群算法[11]和粒子群优化算法[12]等。上述算法在进行航迹规划时，各有优缺点，很难在复杂、规模较为庞大的任务环境模型中快速地规划出最优航迹。由于蚁群算法具有分布式计算、群体智能、正反馈[13]、解的长度可变、解数据处理起来灵活方便等优点，因此被广泛采用。但是蚁群算法也有容易陷入局部最优解的缺点和存在算法堵塞的现象。针对蚁群算法的特点和缺陷，本文提出了算法的改进原则,并基于这些原则提出了新的启发式和信息素更新机制，将改进后的蚁群算法和改进后的Voronoi图相结合，对无人机的航迹进行规划，最后通过仿真验证了算法的高效性，以及算法改进原则的有效性。

1 Voronoi图建模过程

1.1 传统Voronoi图构建及特点

传统Voronoi图将各个相邻的母点按照一定规则相连，生成Delaunay三角形，众多的Delaunay三角形组成Delaunay三角网[14]。生成的Delaunay三角形是一种特殊的三角形，它能保证自己的外接圆不包含其他母点。已有学者证明，Delaunay三角形是最优的[15]。对Delaunay三角形的各条边作垂直平分线，这些垂直平分线所形成的边就是Voronoi图的边，即无人机的可选飞行轨迹。如图1所示，蓝色点代表威胁源，共有50个；蓝色线段代表无人机可选飞行轨迹。但是这样的建模过程没有充分考虑各个威胁源的类型，以及各个威胁源对无人机威胁的大小，因此需要作出改进。

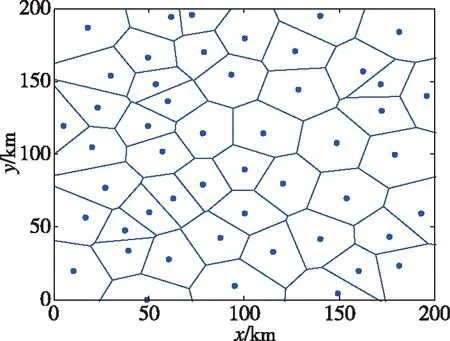
图1 传统Voronoi图Fig.1 Traditional Voronoi diagram

1.2 改进型Voronoi图的构造

如图2所示，A、B、C为三个威胁点，对无人机的威胁程度各不相同，△ABC为Delaunay三角形，则AD的长度为

(1)

式中，LAB为A、B点的间距；LAD为A、D点的间距；TA和TB为A、B的威胁度。同理可以确定F、E点的位置。分别连接D、E、F点，得到分割三角形△DEF，然后作△DEF的内切圆，内切圆的圆心为O点，连接OD、OE、OF，所得的线段OD、OE、OF就是改进型Voronoi图的边。

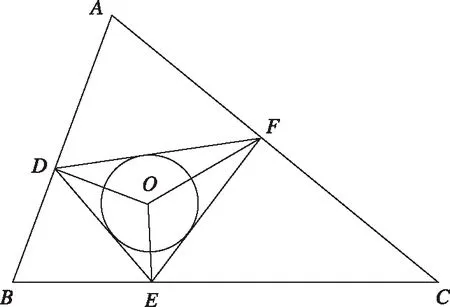
图2 改进型Voronoi图构造过程Fig.2 Construct procedure of the improved Voronoi diagram

如图3所示，蓝色实线为传统Voronoi图，红色实线为改进型Voronoi图。从图3中可以看出，红色实线到两侧威胁源的距离不再相等，红色实线对应的轨迹更偏向于对无人机威胁小的威胁源，较传统Voronoi图更能反映出各个威胁源对无人机威胁的差异性。

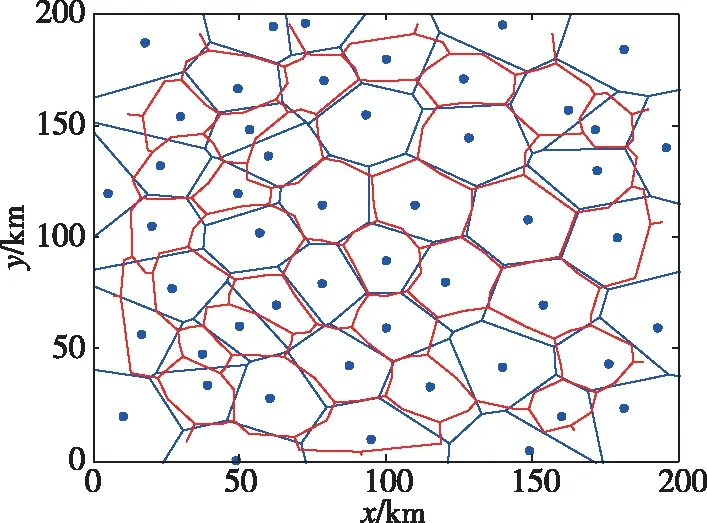
图3 改进型Voronoi图Fig.3 The improved Voronoi diagram

基于Voronoi图规划得到的航迹具有固有的威胁回避能力，无人机的飞行航迹只要在Voronoi图的边中选择即可[16]，而每条边包含两个端点，这些端点就构成了无人机飞行的航迹点。

2 航迹规划

2.1 航迹代价函数

无人机航迹规划的本质是在一定的约束条件下找出从起点到终点能有序地避开威胁区域的最优航迹[17]。由于无人机巡航飞行的高度一般在3000m 以上，无法利用地形因素进行威胁规避机动，因此只考虑其横向运动，航迹规划问题就被简化成为一个二维水平航迹规划问题[18]。采用1.2节中改进型Voronoi图的构图方法，对无人机任务环境进行建模，不考虑禁飞区、障碍区、移动威胁源和面威胁源，则无人机航迹规划就变成在改进型Voronoi图中寻找有序子集，使无人机从起点到终点的航迹代价最小的问题。航迹代价可以为无人机飞行航迹总长，但是据此生成的飞行航迹所受的威胁总代价并不一定是最小的。本文综合考虑飞行航程和飞行过程所受威胁，设计了无人机航迹规划的航迹代价函数如下所示

(2)

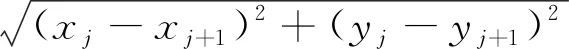
2.2 蚁群航迹规划算法的分析

自然界中，蚂蚁蚁群在觅食过程中形成的轨迹往往是最短的。这个现象产生的原因主要是基于蚂蚁的一个生物群体特征：信息素。蚂蚁会在经过的航迹上留下信息素，信息素又会随着时间逐渐挥发。航迹上经过的蚂蚁越多，则信息素浓度高。随着时间的推移，最优航迹因为路程短，且经过的蚂蚁数量多，航迹上的信息素浓度逐渐升高。蚂蚁自身在前进的过程中，又会选择信息素浓度高的方向前进，则在最优航迹上的蚂蚁数量会越来越多，信息素的浓度也会越来越高，直到信息素的挥发量等于信息素的增加量，此时信息素浓度保持不变，最优航迹与其他航迹被区分开来。

在蚁群寻优过程中，信息素体现了一种对历史信息的记载：路程更短的航迹上信息素浓度更高，信息素浓度高又会引来更多的蚂蚁，更多的蚂蚁又会增加信息素的浓度，这一正反馈机制，就可以引导蚂蚁找到最优航迹。根据蚁群算法原理，信息素是蚁群在觅食过程中对蚂蚁产生吸引作用的信息载体，在一定程度上对算法的收敛速度和航迹规划效果有着十分重要的影响[19]。因此，算法中信息素的更新方式和变化过程，必须能较好地反映出算法逐渐向最优解航迹收敛的过程。

蚁群算法在开始启动时，默认各个点的信息素浓度是一样的。如果算法单纯的只有信息素机制，在算法迭代初期，蚁群算法就类似于群举法，得出最优解航迹的时间太长，所以蚁群算法还有另外一个机制：启发式。启发式的作用是：对蚂蚁产生一种牵引力，促使蚂蚁朝着终点(解航迹)的方向前进。最简单的启发式可以定义为

(3)

式中，(x,y)为当前蚂蚁所在航迹点的某一个可选邻点坐标，(xt,yt)为目标点坐标。当可选邻点到目标点的距离都很远时，此时式(2)是一个小量，各个可选邻点对应启发式的值差异不大，此时启发式不能很好地区分出各个可选邻点的优劣。

为了使算法能更快地收敛于最优解，信息素与启发式在算法迭代过程中对蚂蚁前进过程的影响应该随着算法的迭代而逐渐变化。迭代初期，各个点的信息素浓度差异不大，此时启发式对蚂蚁选择下一个航迹点的影响应该要大一点，约束蚂蚁向着终点的方向前进，即生成初始可行解航迹；当算法迭代到后期时，信息素的影响要大于启发式，从而体现出历史的痕迹。

综上，提出了信息素和启发式的改进原则：

启发式机制改进原则：

1)算法运行初期，启发式的影响要大于信息素；

2)具有明显的使当前解航迹向最优解航迹靠近的趋势；

3)在靠近最优解航迹时，这种趋势要减弱，在最优解航迹附近时，启发式对算法的影响要弱于信息素。

信息素机制改进原则：

1)当靠近最优解航迹时，解的微小变化引起的信息素浓度变化较明显；

2)最优解航迹上的信息素能够自动平衡，并在最优解航迹上达到最大值；

3)信息素值的变化能够明显反映出航迹代价函数值的变化、最优解航迹和次优解航迹的差距。

2.3 蚁群航迹规划算法的改进

假定有50个威胁源，基于2.1节中提出的改进原则，提出了新的启发式和信息素机制。

启发式

(4)

式中，i指第i只蚂蚁，j指第i只蚂蚁的第j个航迹点，即蚂蚁当前所在的点，k指第i只蚂蚁第j个航迹点的第k个可选邻点，ξi,j,k为当前蚂蚁所在航迹点第k个可选邻点的启发式值；φ为启发式极值控制系数，θ为启发式形状因子；li,j为当前蚂蚁所在航迹点到目标航迹点的距离，li,j,k为蚂蚁所在航迹点的第k个可选邻点到目标航迹点的距离。启发式以(li,j-li,j,k)为自变量，表明以当前蚂蚁所在航迹点到目标航迹点的距离为基准，度量可选邻点的优劣，距离目标点更近的可选邻点更优。由式(4)决定的启发式存在极限值，表明可选邻点并不是单纯的距终点越近越好，极限值的存在是为了防止算法陷入局部最优解，无法跳出局部最优解循环。

全局信息素更新中，信息素的增量为

(5)

式中，ρ为信息素挥发系数；Q为信息素修正系数；Ci为第i只蚂蚁经过航迹的航迹总代价；Pr为航迹总代价预估值，计算公式为

(6)

式中，(xs,ys)为起点坐标;U为航迹代价平衡系数。则全局信息素更新为

τi,j=

(7)

其中，Pi,j代表第i只蚂蚁的第j个航迹点；τi,j为第i只蚂蚁第j个航迹点的信息素浓度。

2.4 算法堵塞现象的分析与处理

通过大量的实验发现，在某些特殊的点处，算法会出现堵塞，堵塞现象会降低算法的运行速度，甚至会使算法陷入死循环。因此，为了提高算法的运行速度，不得不考虑堵塞现象。

堵塞现象的处理分为以下几种情况：

1)如图4所示，蚂蚁的前进路线为A→B→C→D→B→C，此时蚂蚁在C点，满足约束条件的可选邻点为B点和D点，而B、D两点都在航迹中，D点出现一次，B点出现两次，此时选择出现次数少的邻点作为下一个航迹点，即选择D点。

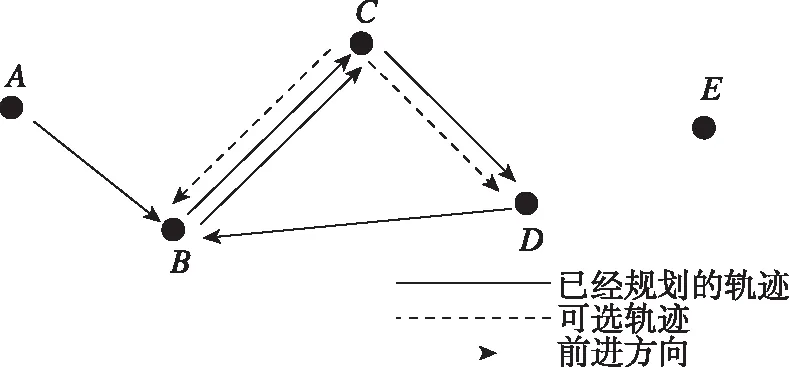
图4 第一种停滞现象Fig.4 The first stagnation

2)如图5所示，蚂蚁的前进路线为A→B→C→D→B→C，此时蚂蚁在C点，满足约束条件的可选邻点为E点和D点，E点不在航迹中，D点在航迹中。针对这种情况，此时已经在航迹中出现过的可选邻点的状态转移公式为

(8)

式中，ηi,j,k为已经在航迹中出现过的可选邻点的选择概率;μ为重复点选择概率系数;λk为可选邻点在航迹中出现的次数;α为信息素权重系数;β为启发式权重系数;m为第i只蚂蚁第j个航迹点的可选邻点数。

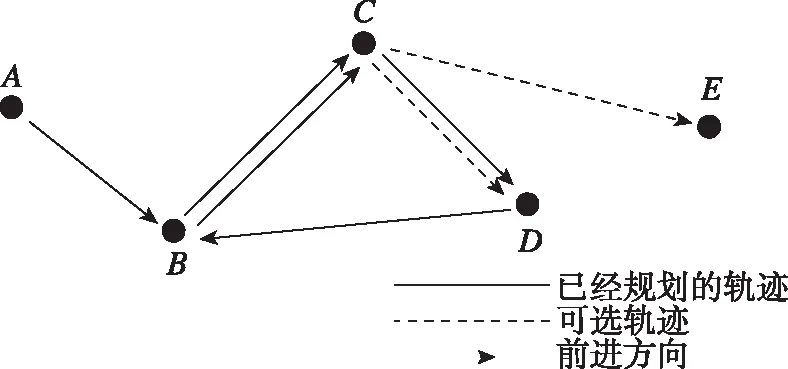
图5 第二种停滞现象Fig.5 The second stagnation

未在航迹中可选邻点的状态转移公式为

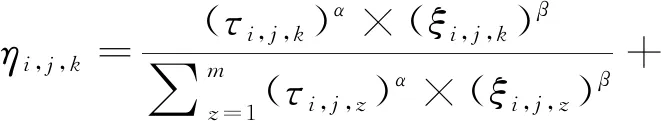
(9)

式中，h为第i只蚂蚁第j个航迹点的在航迹中已经出现过的可选邻点数目。

3 蚁群航迹规划算法设计

根据改进型Voronoi图对任务环境进行建模，在此基础上，利用改进后的蚁群航迹规划算法求解无人机航迹规划问题的算法流程如图6所示。

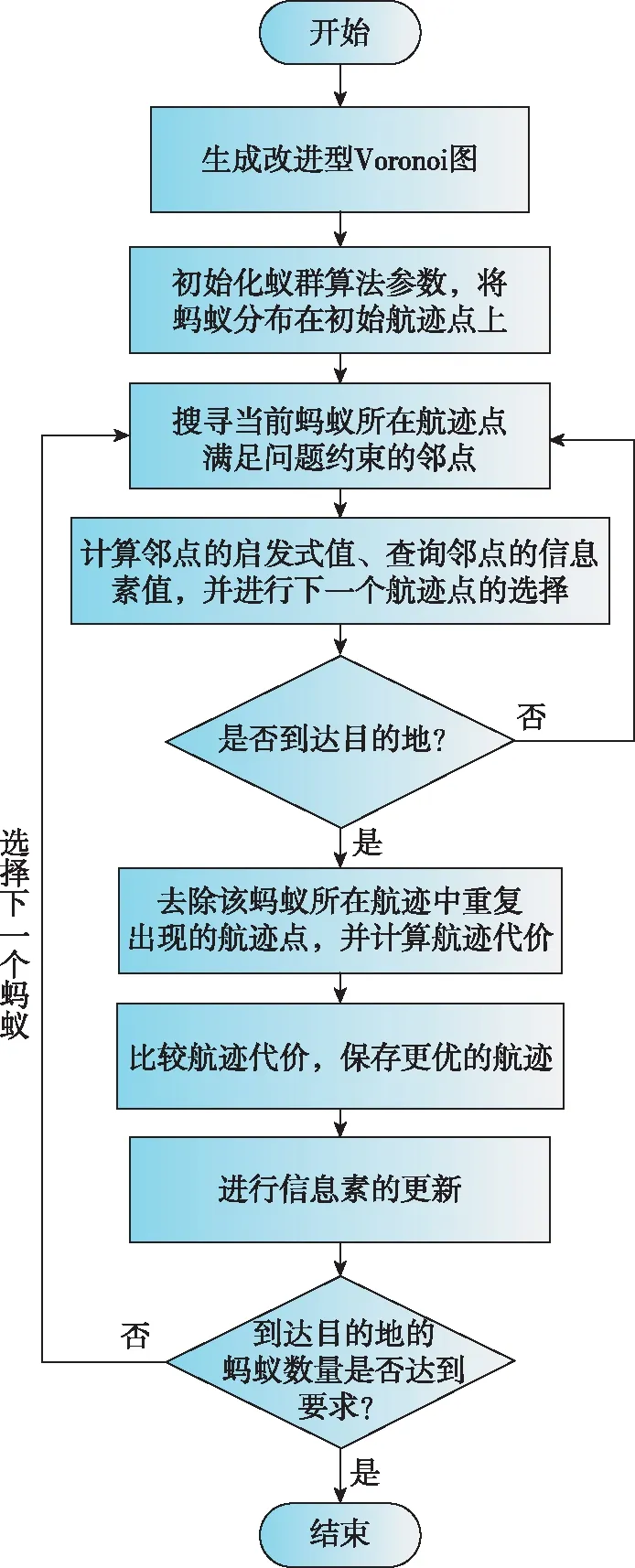
图6 算法流程Fig.6 Algorithm flow chart

4 实验仿真

假定在200km×200km的数字地图上，分布有50个威胁源，如图3所示。在本文仿真中，蚂蚁数量为200只，单次循环终止时需到达目的地的蚂蚁数量为100只，信息素权重系数α=1，启发式权重系数β=1，信息素挥发系数ρ=0.2，重复点选择系数μ=0.5，信息素初始值和最小值为1.0，信息素修正系数Q=3，信息素扩散系数ζ=0.4，由航迹代价函数可知，航迹代价平衡系数U=2，启发式极值控制系数φ=10，启发式形状因子θ=0.4。每一次实验循环5次，在Windows 10-64bit，Matlab 2014a平台进行1000次仿真实验，并与传统蚁群算法进行对比，结果如表1所示。

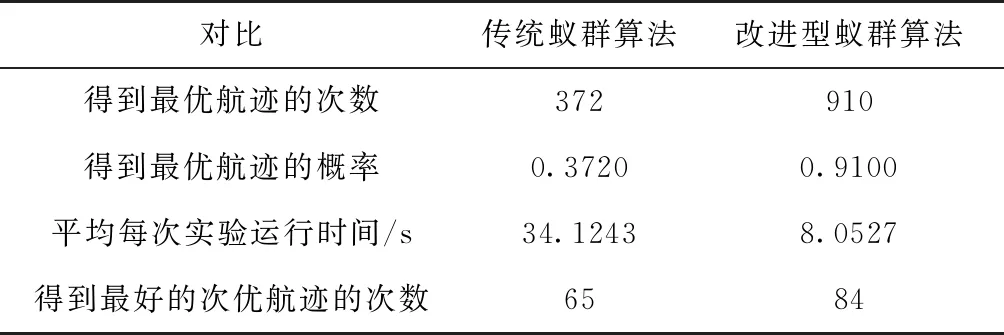
表1 蚁群算法实验对比

由表1可知，改进型蚁群算法得到最优航迹的概率较传统蚁群算法提高了144.62%，运行时间缩短了76.40%，得到最好的次优航迹的次数也提高了19次，可见，改进型蚁群算法的性能得到了大幅度的提升。

利用改进型蚁群算法，基于传统Voronoi图与改进型Voronoi图的航迹规划结果如图7和图8所示，两者的最优航迹实验数据对比结果如表2所示。

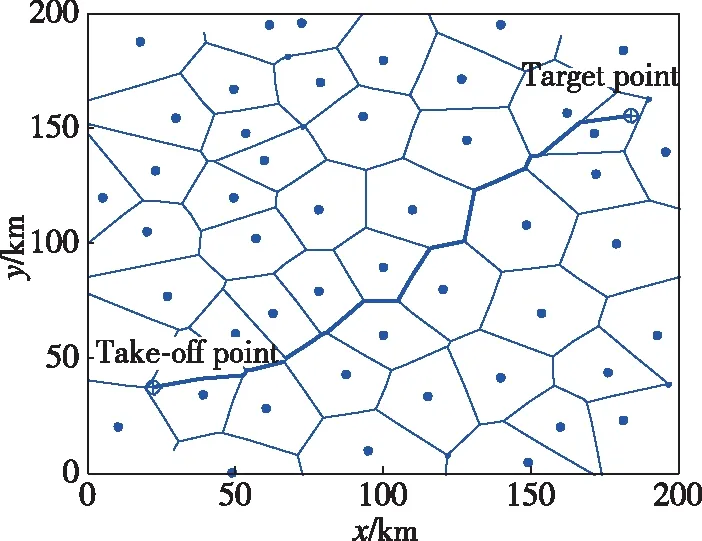
图7 传统Voronoi图最优飞行航迹Fig.7 The optimal trajectory of the traditional Voronoi diagram

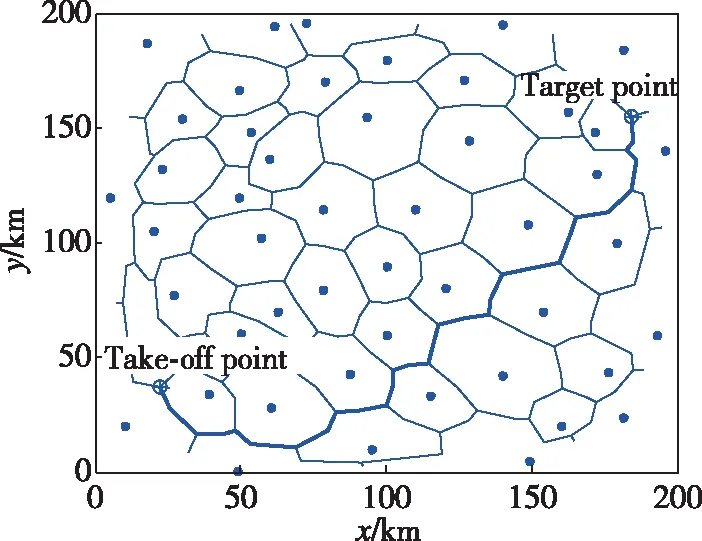
图8 改进型Voronoi图最优飞行航迹Fig.8 The optimal trajectory of the improved Voronoi diagram

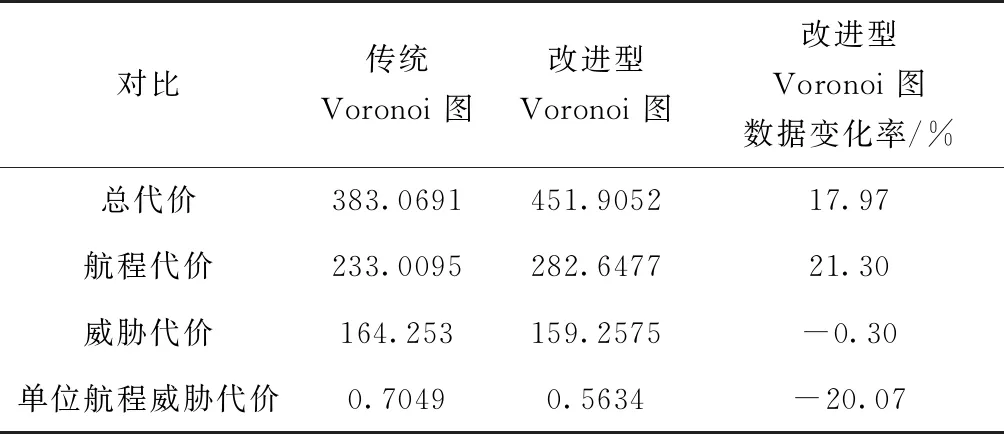
对比传统Voronoi 图改进型Voronoi 图改进型Voronoi 图数据变化率/%总代价383.0691451.905217.97航程代价233.0095282.647721.30威胁代价164.253159.2575-0.30单位航程威胁代价0.70490.5634-20.07

由表2可知，改进型Voronoi图的航程代价增加了21.30%，威胁代价却基本没变。从图8可以看出，航程代价增长的部分是因为规划生成的航迹有明显的迂回规避意图，从而增加了航程；改进型Voronoi图的单位航程威胁代价比传统Voronoi图降低了20.07%，为无人机提供了一条更安全的飞行航迹。在无人机执行任务过程中，与其他因素相比，首先要降低无人机被威胁源发现、干扰和攻击的可能性，以保证无人机能够安全顺利地完成任务，因此，改进型Voronoi图更贴近真实任务环境。

式(4)中，启发式随(li,j-li,j,k)的变化过程如图9所示。由图9可知，启发式的极限值约为60，当(li,j-li,j,k)=0时，启发式基准值为32.5。

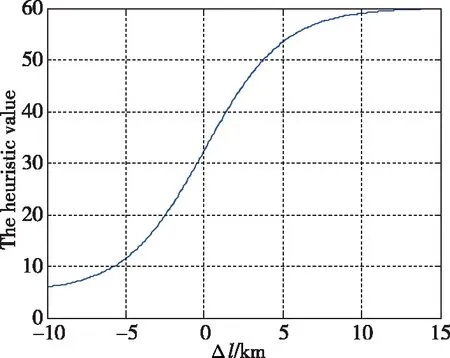
图9 启发式变化过程Fig.9 Changing process of heuristic value

进行多次航迹规划实验，统计20次输出为最优航迹的程序运行结果，并对这20次程序运行过程中，每次循环的最大信息素值和航迹代价函数值取平均值，得到每次循环的最大信息素值均值和航迹代价函数值均值随迭代次数变化的过程，如图10所示。

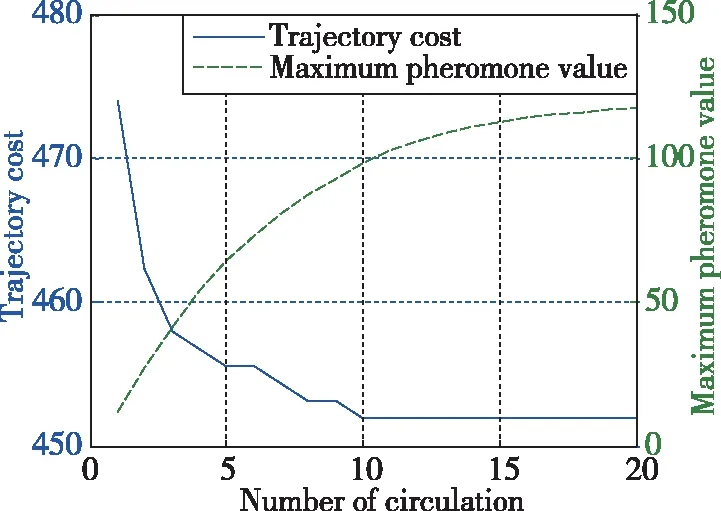
图10 航迹代价和最大信息素变化过程Fig.10 Changing process of trajectory cost and maximum pheromone value

从图10中可以看出，随着迭代次数的增加，航迹代价迅速减小，最大信息素值迅速增加，表明航迹规划过程中，当前航迹正迅速向最优航迹靠近，满足启发式机制改进原则2)和信息素机制改进原则1)和3)；当迭代次数为1时，最大信息素均值为11.5982，小于启发式基准值32.5，此时启发式机制的作用大于信息素机制；经过5次迭代，最大信息素均值为64.3286，已经大于启发式的极限值，此时信息素机制的作用大于启发式机制，满足启发式机制改进原则1)和3)；当迭代次数大于10时，航迹代价已基本不变，此时算法已得到最优航迹；当迭代次数为20时，最大信息素均值趋于稳定，满足信息素机制改进原则2)。