基于SVM的高校考研预测模型研究

张 凯，闫立强，刘 畅，杜亚冰

(河南城建学院，河南 平顶山 467036)

是否报考研究生是本科生毕业前面临的重要选择之一，若能对考研结果进行预测，将对本科生的报考决策和学校分类教学管理产生积极影响。目前，已有一些文献使用机器学习算法研究考研预测问题，如李楠等提出基于Logistics算法的考研成绩变量预测方法[1]；王西平提出了改进加权的KNN算法考研预测模型[2]；郑宝乐等提出了基于线性判决分析降维(LDA) 结合支持向量机(SVM) 建立学习模型的方法[3]；黄炎对比了朴素贝叶斯算法、线性回归和决策树相结合的算法、LIBSVM向量机等三种算法的考研结果预测准确率[4]；李驰利用基于遗传算法优化的BP神经网络对考研结果进行了预测[5]；张凤霞等选取若干个家庭因素、个人因素、校园因素和专业因素等作为特征子集，使用CSVM、PSVM、TSVM分别对报考意愿进行了预测[6]。这些文献大多将已报考学生的在校成绩作为样本集训练预测模型，取得了较高的准确度。

图1 分阶段考研预测示意图

考研预测按时间顺序可划分为“意愿预测”和“结果预测”(含成绩预测)(见图1)。“意愿预测”是在报考前，预测是否报考；“结果预测”是在报考后，预测考研结果(含考研成绩)。以上文献均为“意愿预测”或“结果预测”。而从考研预测的实际场景出发，若合并两种预测，将会大大增加预测模型的实用性，因此，本文尝试以报考前某校所有理工科本科生的学业成绩作为样本集，建立一种基于支持向量机的考研结果预测模型。

1 支持向量机

(1)

s.t.yi[(wxi)+b]≥1i=1,2,…,l

(2)

对线性不可分问题，引入一个松弛变量ξ≥0，可调的惩罚因子C，则二次规划问题就变成：

(3)

s.t.yi[(wxi)+b]≥1-ξi=1,2,…,l

(4)

为了求解此二次规划问题，引入Lagrange函数：

(5)

其中αi>0为Lagrange乘子，求解后得到最优分类函数[9]为：

(6)

其中：α*为最优解，b*为最优偏置。

SVM通过选择满足Mercer条件的核函数K，即K(x,y)=ø(x)·ø(y)，将输入空间映射到高维特征空间(一般是Hiber空间)，即对x作从输入空间Rn到特征空间H的变换：

x→ø(x)=(ø1(x),ø2(x),…,øl(x))T，

(7)

在这个高维特征空间中求解最大间隔分类超平面，求解后得到最优分类函数[10]为：

(8)

2 核函数

选择常用的内积(dot)、径向基(RBF)、多项式(polynominal)等核函数分别进行模型训练，通过对比结果，找到评估结果最优的核函数建立预测模型。

(1)内积核函数：

K(x,y)=x*y

(9)

(2)径向基核函数：

K(x,y)=exp(-γ‖x-y‖2)

(10)

(3)多项式核函数：

K(x,y)=(x*y+1)d

(11)

其中，可调参数d是多项式的次数。

3 SVM考研结果预测模型

3.1 数据准备

影响报考决策和考研结果的因素很多，如：高考成绩、在校各科成绩及排名、英语四六级考试成绩、专业方向、就业前景、奖惩情况、家庭情况等[6]。这些影响因素内部和相互之间的关系复杂。虽然属性越多，预测准确度越高，但是数据采集、数据清洗、模型建立等工作难度也会随之增大，模型的执行效率随之降低。为增大模型的适用范围、降低复杂性，本文选择脱敏后的某校2020届、2021届4年制本科在生源地的理工毕业生的高考成绩和在校成绩作为样本数据，有效样本数分别为1 612、1 504，合计3 116。考研结果作为样本标签，属性值为“Y”、“N”，分别对应“被录取”、“未报考或未被录取”。

理工科考研的科目一般为外语、政治、数学和专业课。为适用所有理工科专业，本文选择考研科目相同且全校统考的科目成绩作为数据集。这些科目包括高等数学(上/下)、线性代数、大学英语(一至四)、思想政治理论课等11门科目的成绩以及高考语文、数学、外语、外语听力和综合等5门科目的成绩。由于高校内不同科目的难易程度、考试类型不同，为增加成绩的区分度，本文选取各科目的期末考试成绩，不含平时成绩、期中考试成绩。

3.2 数据预处理

在数据采集与考研结果统计过程中，由于人为因素会导致个别数据不准确或数据缺失现象，但基于高质量的数据分析出的结果才更具有价值，所以首先要进行数据预处理，以清洗掉数据中的错误。本文将存在数据重复、部分数据缺失等问题的极少量样本直接删除，只保留完整、准确、无空缺、无异常的数据值。

3.3 数据标准化与特征选择

数据的标准化(normalization)是将数据按比例缩放，使之落入一个小的特定区间。最典型标准化方法是数据的归一化处理，常见的数据归一化方法有：min-max标准化、log函数转换、atan函数转换、z-score标准化。本文采用常见的z-score标准化。这种标准化是从所有值中减去数据的均值，然后除以标准差。z-score方法的转换函数为：

(12)

式中：μ为数学期望；σ为标准差。

本文采用Relief算法进行特征选择。Relief算法最早由Kira等[11]提出，主要解决两类的分类问题，是公认效果较好的 filter 式特征评估算法。它根据各个特征和类别的相关性赋予特征不同的权重，移除权重小于某个阈值的特征[12]。通过Relief算法过滤无关特征后，特征子集为高数上、高数下、高考外语听力、高考外语、高考综合、高考数学等(见表1)。

表1 Relief算法评估的特征权重

图2 特征子集的箱线图

特征子集的箱线图如图2所示。由图2可以看出，选择的6个样本特征没有明显的离群点。

3.4 建立模型

(1)划分样本集

将2020届、2021届毕业生的样本集分别定义为S1、S2，合集定义为S，即S=S1+S2。样本集划分为3种形式，均采用分层抽样(如表1所示)。

样本集a：将S1作为训练集、S2作为测试集；样本集b：将S2作为训练集、S1作为测试集；样本集c：将S的70%作为训练集、30%作为测试集。

(2)选择评估指标

三个样本集中的阳性样本与阴性样本的比例均显著不平衡(约18)，不能简单地采用单值评估指标，而多值评估指标将会提高模型比较的难度，因此本文采用F-measure指标，该指标将阳性查全度和阳性查准度合并为一个单值，即

(13)

式中：precision为阳性查准度

(14)

recall为阳性查全度。

(15)

β为用户对阳性查全度的重视程度，是阳性查准度的倍数，本文β取1。

图3 三种SVM模型对三种样本集的测试结果F1-measure

(3)训练模型

采用5折交叉验证法，分别使用三种核函数、三种样本集训练SVM模型。三种核函数的惩罚参数C均取0，超参数γ取1.0、d取2.0。基于三种样本集、三种核函数训练的SVM模型测试指标F1-measure如图3所示。

由图3可以看出：采用内积核训练的SVM模型的测评结果F1-measure值比径向基核和多项式核的都高；采用内积核和径向基核的SVM模型对三个样本集的测试结果F1-measure值差异较小。因此，本文选择内积核作为考研结果预测模型的核函数。

(4)网格搜索算法超参数寻优

本文采用网格搜索算法对基于内积核的SVM模型超参数寻优。寻优过程使用样本集c，训练集与测试集比例为73。从寻优过程(见图4)可以看出，通过网格搜索算法找到的最优结果对应的C值为2.2。惩罚参数C、参数间隔设置及结果最优时的相应值如表2所示。

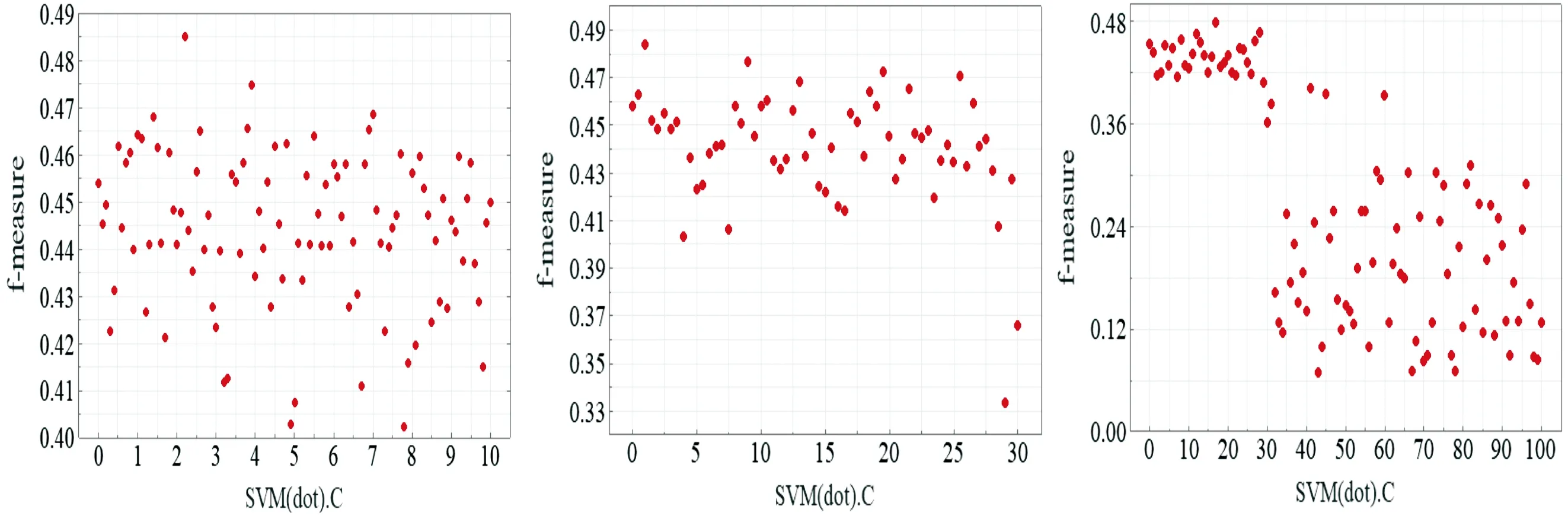
(a)c∈{0～10} (b)c∈{0～30} (c)c∈{0～100}

(d)c∈{0～1 000} (e)c∈{0～10 000}

表2 基于内积核的SVM模型超参数寻优设置

3.5 结果分析

分别使用三个样本集，对基于内积核的SVM模型进行训练和测试，惩罚参数C设置为2.2，测试结果如表3所示。从表3可以看出，在三个样本集的测试结果中，准确度、查全度、差准度、AUC、F1-measure等指标比较接近，说明基于内积核的SVM模型对不同样本集的预测能力较稳定。

表3 基于内积核的SVM测试结果

三个样本集对应的测试结果混淆矩阵如表4所示。从表4可以看出：(1)本文模型预测的选择报考并被录取的学生中平均有66.44%被预测错误，这部分学生存在报考并被录取的可能，学校可以鼓励这部分学生积极报考；(2)本文模型预测的未选择报考或未被录取的学生中平均约有90%预测正确，阴性查准度较高，学校可以鼓励这部分学生创新创业或提高与就业相关的专业技能；(3)报考并被录取学生中约71%与模型预测结果一致；(4)使用不同年份的样本分别作为训练集和测试集，模型测试结果基本稳定。

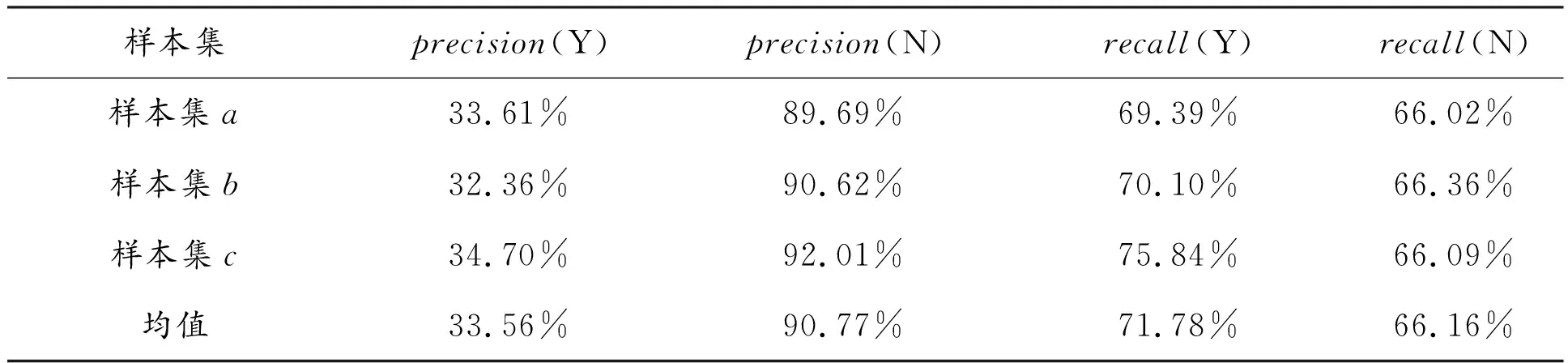
表4 三个样本集对应的混淆矩阵结果

4 对比实验分析

分别采用本文SVM算法、文献[1]中的Logistic回归分类算法和文献[2]中的kNN算法对样本集c训练测试，对比测试结果如表5所示。其中kNN算法采用网格搜索算法找到最优结果对应的k值为2(参数寻优过程见图5)。由表5可以看出，Logistic回归算法的AUC值与本文SVM算法相近，且其accuracy、precision值均为最高，但其综合评价指标F1-measure值明显较低。说明此算法对于标签比例不均衡的样本集c来说，预测效果较差。kNN算法的F1-measure值、AUC值、recall(Y)、precision(Y)均比本文SVM算法低。本文SVM算法对于样本集c的训练测试结果明显优于Logistic回归算法、kNN算法。

表5 三种算法的对比测试结果

图5 kNN算法的参数寻优过程

5 结论

为更加贴合实际的考研预测场景，采用上一年样本数据训练模型，预测下一年的考研结果，本文将两年的样本数据集分为三种样本集分别进行训练建模。通过对比实验，本文SVM算法建立的预测模型综合预测能力优于Logistics算法、kNN算法。本文模型选择的样本数据获取直接、训练方法简单、训练时间短，适用于学校层面对所有理工科的所有专业学生进行考研预测，可以协助学校有针对性地指导学生做出报考决策。对预测结果为阳性的学生偏重指导理论学习，对预测结果为阴性的学生偏重培养职业技能。下一步的研究工作可以考虑利用其他机器学习方法或优化方法，尝试引入更多的因素，例如学生报考信息、四六级英语考试成绩、文科学生成绩等，以提高模型的预测精度和适用范围。