形散神聚：一道课本例题的变式

文 康敏

数学的知识点是固定的，但是数学问题是千变万化的，怎样快速解决问题，这就需要找准题目的突破口。如：全等三角形是通过图形的运动——平移、翻折、旋转，形状、大小不变，位置发生变化；相似三角形就是大小改变，其他类比全等三角形。所以证明三角形全等或相似的关键是通过已知条件找寻哪两个三角形通过怎样的运动而来。今天我们就来研究旋转运动形成的全等三角形。

原题呈现（苏科版数学教材八年级上册第15页例题）已知：如图1，AB、CD相交于点E，且E是AB、CD的中点。求证：△AEC≌△BED。

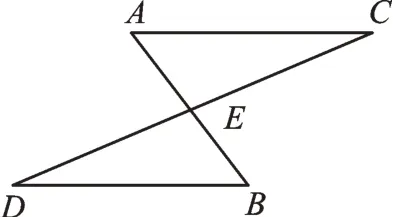
图1

【解析】本题考查的是全等三角形的证明。观察图形，我们首先发现对顶角相等（∠AEC=∠BED），即点E与自身是对应关系；再由已知条件“E是AB、CD的中点”，得到AE=BE，CE=DE，从而运用“边角边”证明出三角形全等。

【总结】本题从运动的角度可以看作是△AEC绕着点E顺时针（或逆时针）旋转180°得到的△BED，这样就明确了两个三角形的对应点、对应边、对应角。通过看图直接得到一组角相等，再由已知条件得到所需要的两组边对应相等，这样满足两边及其夹角对应相等，从而证明出结论。

本题将图形旋转180°是很特殊的角度，若旋转的是其他角度呢？

变式1如图2，等腰Rt△ABC、等腰Rt△EDC中，∠ACB=∠ECD=90°，连接AE与BD相交于点F，求AE与BD的关系。

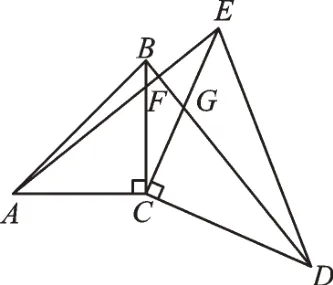
图2

【解析】我们可以先猜测AE=BD，然后倒推它们所在的三角形是否全等。AE与BD所在的三角形分别是△AEC与△BDC，由等腰三角形的两腰相等，得AC=BC，EC=DC。而第三组边相等是要证明的，那么只能找两边的夹角。由∠ACB=∠ECD=90°，运用等式的性质，两边同时加上公共角∠BCE，得出∠ACE=∠BCD，运用“边角边”得到△AEC≌△BDC，得AE=BD。由全等还可得∠AEC=∠BDC，再由对顶角相等得∠BGE=∠CGD，运用三角形内角和 公 式 求 出∠EFG+∠AEC+∠BGE=180°，∠DCG+∠BDC+∠CGD=180°，从而求出∠EFG=∠ECD=90°，所以AE⊥BD。

【总结】本题从运动的角度可以看作是△ACE绕着点C顺时针旋转90°得到的△BCD。题目所给的直接条件是两组对应边分别相等，再证明两边的夹角也相等就可以证明三角形全等，从而得出AE与BD的两种关系：数量关系是相等，位置关系是垂直。从动态的角度再次变化，题目不变，如图3。思路同上，与变式1的区别在于，由∠ACB=∠ECD，运用等式的性质，两边同时减去公共角∠BCE，求出∠ACE=∠BCD。

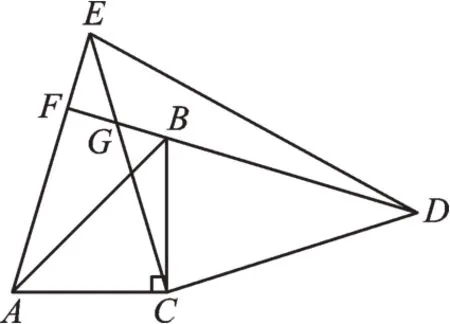
图3

如果把等腰直角三角形换为等边三角形又会如何？

变式2如图4，△ABD、△ACE都是等边三角形，DC、BE相交于点P，求∠EPC的度数。

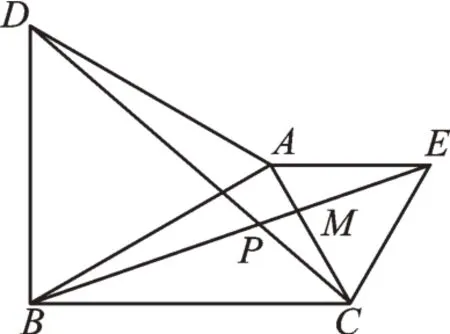
图4

【解析】从题目的已知条件中能获得哪些信息？等边三角形三条边相等，三个角都是60°。那么从图形上观察，有没有三角形全等？有了前两题的经验，我们能发现△DAC绕着点A逆时针旋转60°得到△BAE，从而可证得∠DCA=∠BEA。这两个角又可放在成“8字形”的△PCM与△AEM中，由∠PMC=∠AME和三角形内角和定理，等量代换后得出∠EPC=∠EAC=60°。

变式3如图5，在正方形ABCD与正方形AEFG中，连接DE、BG相交于点P，问DE与BG的关系，并说明理由。

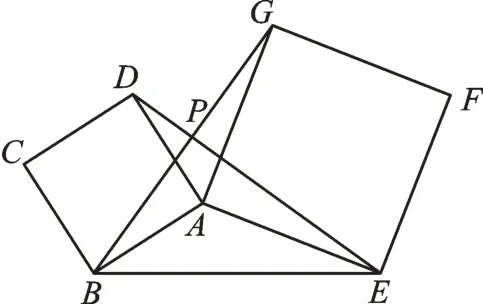
图5

【解析】由四边形ABCD与四边形AEFG都是正方形，可以得到BA=DA，GA=EA，∠BAD=∠GAE=90°。DE与BG分别是△DEA与△BGA的边，那么我们就能发现△BGA绕着点A顺时针旋转90°得到△DEA，证出△BGA≌△DEA，得出DE=BG，再类比前几题的证明得出DE⊥BG即可。

变式4如图6，在菱形ABCD与菱形AEFG中，∠BAD=∠EAG=70°，连接DE、BG相交于点P，求∠BPD的度数。

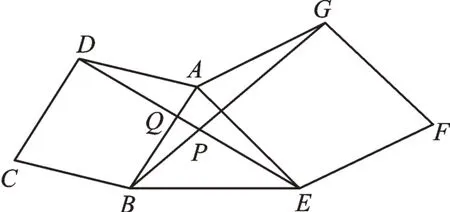
图6

【解析】由四边形ABCD与四边形AEFG都是菱形，可以得到BA=DA，GA=EA。由∠BAD=∠EAG=70°，本题就可以看作是△BGA绕着点A顺时针旋转70°得到的△DEA。然后只需要说明∠BAG=∠DAE，就能证明△BGA≌△DEA，最终求出∠BPD=70°。

【总结】这几题考查的知识点类似，都是通过观察找寻三角形是经过怎样的旋转变换得出另一个三角形。而具体要证哪两个三角形全等，则通过条件求出两组边对应相等且所夹的角也相等即可。