函数典型例题与解题策略

文 李祥

由数轴上的点与实数的对应关系到正、反比例函数，由一次方程（组）、不等式（组）到一次函数，由一元二次方程到二次函数等，我们不难发现，函数是贯穿初中数学的一条主线，具有承上启下的作用。函数是初中数学的重点，也是难点，更是中考命题的主要考查对象。

一、函数的概念与性质

例1已知一次函数y=（3a-2）x+（1-b），求字母a、b的取值范围，使得：

（1）y随x的增大而增大；

（2）函数图像与y轴的交点在x轴的下方；

（3）函数图像过第一、二、四象限。

【思路点拨】对于y=kx+c（k≠0）的图像，当k＞0时，y随x的增大而增大；当c＜0时，函数图像与y轴的交点在x轴的下方；当k＜0，c＞0时，函数图像过第一、二、四象限。

解：（1）由一次函数y=kx+c（k≠0）的性质可知：当k＞0时，函数值y随x的增大而增大，即，且b可取任何实数。

（2）函数图像与y轴的交点为（0，1-b）。

∵交点在x轴的下方，

【总结升华】下面是y=kx（k≠0），y=kx+b（k≠0）的图像的特点和性质示意图。如图1，当k＞0时，y随x的增大而增大；当k＞0，b＞0时，图像过第一、二、三象限；当k＞0，b=0时，是正比例函数；当k＞0，b＜0时，图像过第一、三、四象限。当y=x时，图像过第一、三象限，且与x轴的夹角为45°。由于常数k、b不同，可得到不同的函数，k决定直线的倾斜程度，b决定直线与y轴交点的位置，由k定向，由b定点。同样，图2是k＜0的各种情况，请同学们自己尝试指出它们的特点和性质。

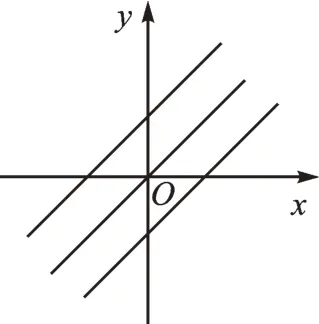
图1

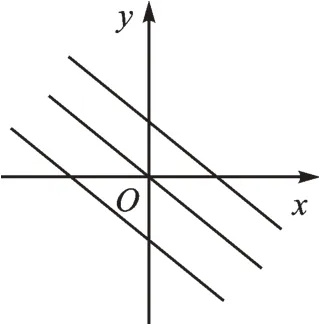
图2

二、函数的图像及性质

例2已知一次函数y=kx+b（k≠0）的图像经过A（3，18）和B（-2，8）两点。

（1）求一次函数的表达式；

（2）若一次函数y=kx+b（k≠0）的图像与反比例函数的图像只有一个交点，求交点坐标。

【思路点拨】（1）用待定系数法求一次函数的表达式；（2）联立一次函数表达式和反比例函数表达式，根据题意得到Δ=0，解方程即可得到结论。

解：（1）把（3，18），（-2，8）代入一次函数y=kx+b（k≠0），得

∴一次函数的表达式为y=2x+12。

（2）∵一次函数y=kx+b（k≠0）的图像与反比例函数的图像只有一个交点，只有一组解，

所以2x2+12x-m=0有两个相等的实数根，

∴Δ=122-4×2×（-m）=0，

∴m=-18。

把m=-18代入2x2+12x-m=0求得该方程的解为x=-3，经检验符合题意。

把x=-3代入y=2x+12，得y=6，

∴所求的交点坐标为（-3，6）。

【总结升华】本题考查了用待定系数法求一次函数表达式、反比例函数与一次函数的交点问题。第（2）问的关键是转化成关于x的一元二次方程，再根据交点只有一个得出根的判别式为0，从而求出m，进而求出交点坐标。

三、二次函数的综合运用

例3二次函数y=ax2+bx+c的图像如图3所示，下列结论：①ab＞0；②a+b-1=0；③a＞1；④关于x的一元二次方程ax2+bx+c=0的一个根为1，另一个根为其中正确结论的序号是_______。

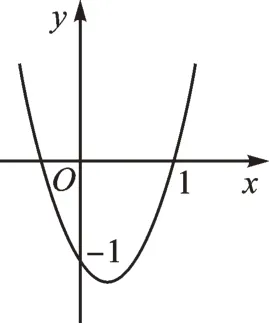
图3

【思路点拨】根据抛物线的开口方向和对称轴判断a与b的符号，由抛物线与y轴的交点得出c的值，然后根据抛物线与x轴交点的个数及x=1时二次函数的值的情况进行推理，进而对所得结论进行判断。

解：①由二次函数的图像开口向上可得a＞0，对称轴在y轴的右侧，b＜0，∴ab＜0，故①错误；

②由图像可知抛物线与x轴的交点为（1，0），与y轴的交点为（0，-1），

∴c=-1，∴a+b-1=0，故②正确；

③∵a+b-1=0，∴a-1=-b，

∵b＜0，∴a-1＞0，

∴a＞1，故③正确；

④∵抛物线与y轴的交点为（0，-1），

∴抛物线的方程为y=ax2+bx-1，

∵抛物线与x轴的交点为（1，0），

∴ax2+bx-1=0的一个根为1，根据根与系数的关系，另一个根为，故④正确。

故答案为②③④。

【总结升华】本题考查的是二次函数与图像结合的综合运用，掌握二次函数的性质、灵活运用数形结合思想是解题的关键。