计及天气因素影响的风-光-火-储联合发电策略研究

2021-04-14曾柏琛于若英

水力发电 2021年1期

曾柏琛，王琦，于若英，陈宁

(1.南京师范大学电气与自动化学院，江苏南京210046；2.中国电力科学研究院有限公司，江苏南京210000)

新能源的迅速发展带来严重了的消纳问题[1-2]，其主要原因来自火电(核电)机组深度调峰压力过大以及响应速率不高，对此使负荷发生“时移”是解决其消纳问题的重要思路。抽水蓄能电站具有启动迅速、功率调节速度快等特点，可以为新能源并网提供保障和支撑，确保波动性及间歇性很强的新能源无法输出连续稳定的功率时，不会对电网功率平衡造成较大影响，减小新能源并网的不确定因素对电网的冲击从而缓解电网调节压力[3]。

国内外已有不少学者针对含抽水蓄能系统的优化调度开展了研究，文献[4-9]研究了抽水蓄能电站对于可再生能源消纳能力的提升以及其经济性的改善，表明抽水蓄能电站机组的调节性能非常强，升降负荷的速度较快，合理调度对其运行意义重大。

水库水量是抽水蓄能电站的能量载体，其受天气因素影响较大。以往对抽水蓄能电站的研究较少考虑天气因素对于抽水蓄能电站水量的影响，鉴于此本文拟提出一种计及天气因素影响的风-光-火-储联合发电策略，首先考虑天气因素对抽水蓄能电站进行建模，完善更为精确的水量模型；在此基础上将该模型应用于风光-抽水蓄能-火电机组微电网联合模型；最后，根据每日负荷曲线预测结果，利用抽蓄日充放电次数决策方法，提出联合发电策略。本文拟结合宁夏自治州气候气象条件结合电网实际进行仿真，对新能源简单系统和宁夏电网进行算例分析，对所提策略的可行性进行验证，结论证明所建模型可以更加精确的考虑抽水蓄能电站的运行状况，所提策略可以提高微电网运行的经济性。

1 考虑天气因素的抽水蓄能电站模型

1.1 天气因素对于水库的影响

对于抽水蓄能电站的水库而言，水库水面蒸发是其水量损失中非常重要的一部分。各计算时段(月、年)的蒸发损失

Wz=EsFk

(1)

式中，Wz为单位时间内的水库水量蒸发损失，m3；Fk为计算时段内的平均水库面积，m2；Es为计算时段内库区水面蒸发深度，m。

蒸发量的实际值测量较为复杂，可在采用以往的数据进行预测，具体公式为

(2)

式中，αev(k)为抽水蓄能电站库区k时段的蒸发量，m3；Wz(i)为第i月平均蒸发量，m3；D为该月采样时间段总数；Pev为当日蒸发概率。

同理，对于降水量可得

WJ=EJFk

(3)

(4)

式中，WJ为单位时间内增加的水库降水水量，m3；Fk为计算时段内的平均水库面积，m2；EJ为计算时段内库区降水量，m；βpr(k)为抽水蓄能电站库区k时段的降水量，m3；WJ(i)为第i月平均降水量，m3；Ppr为当日降水概率。

1.2 抽水蓄能电站功率建模

本文研究对象为天气因素对于抽水蓄能电站调峰能力的影响问题。在天气因素对于抽水蓄能电站水库水量造成较大影响时，抽水蓄能系统可以通过调节运行方式以及抽蓄时间等，从而改善其对于新能源的消纳能力以及其运行的经济性。

抽水蓄能电站有2种工作模式，蓄能模式与发电模式，实质是电能到重力势能的相互转换，其转换效率与电机功率有关。水量变化如图1所示。

图1 上下水库水量变化示意

水库的模型为

V(u，k)=αev(k)-βpr(k)+(Q(Pump，k)-Q(Tur，k))Δt+V(u，k-1)

(5)

V(d，k)=αev(k)-βpr(k)-(Q(Pump，k)-Q(Tur，k))Δt+V(d，k-1)

(6)

式中，V(u，k)、V(d，k)分别为k时段上、下水库的实际库容，m3；Q(Pump，k)、Q(Tur，k)分别为k时段抽水、放水的流量，m3/s；Δt为时间段时长，15 min。

重力势能与能量转换模型为

P(Pump，k)=-ηPumpρgQ(Pump，k)h

(7)

P(Tur，k)=-ηTurρgQ(Tur，k)h

(8)

式中，P(Pump，k)为k时蓄能功率，kW；Q(Pump，k)为流量，m3/s；ηPump为蓄能效率；P(Tur，k)为发电机组功率，kW；Q(Tur，k)为流量，m3/s；ηTur为发电机组效率；ρ为水密度，取1 000 kg/m3；g为重力加速度，m/s2；h为水库的水头高度，m。

同时由于抽水蓄能电站不可以同时工作运行在发电模式与蓄能模式，但是可以同时处于待机状态，工作状态可以用数学关系表达

U(Tur，k)+U(Pump，k)≤1

(9)

式中，U(Tur，k)、U(Pump，k)分别表示抽水蓄能电站处于发电模式、蓄能模式的状态变量，1为处于该状态，0为不处于该状态。

为了抽水蓄能电站能够满足安全稳定正常的运行抽水蓄能电站库容约束为

(10)

式中，Vumin、Vumax分别表示上水库库容的上、下边界，m3；Vdmin、Vdmax分别为下水库库容的上、下边界，m3；ΔVumax、ΔVdmax分别为抽水蓄能电站上、下水库水量单位时段变化的最大值，m3；采样时间为15 min。

由于抽水蓄能电站在使用中常常与电网相连需要满足功率平衡条件，平衡条件为

P(Pump，k)+P(L，k)=P(Tur，k)+P(g，k)

(11)

式中，P(L，k)、P(g，k)分别为k时负荷与电网的功率大小，kW。根据上述条件可以建立抽水蓄能电站的功率模型，从而分析抽水蓄能电站的调节能力。

2 计及运行经济性的风-光-火-储联合调节策略

2.1 目标函数

以风-光-火-储联合系统运行成本最小为目标。目标函数表示为

(12)

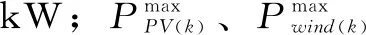
2.2 约束条件

针对最优经济效益运行模型的目标函数，建立等式约束条件。为了保持电力系统电量平衡，需要建立等式约束

P(Tur，k)-P(Pump，k)+Pwind(k)+PPV(k)+Pc(k)=P(L，k)

(13)

同时需要规定各机组运行边界，建立不等式约束条件。

功率范围约束

(14)

(15)

(16)

(17)

(18)

正负旋转备用容量约束[10]

(19)

(20)

启停次数约束[4]

KPump≤M

(21)

KTur≤M

(22)

式中，KPump为水泵的日启停次数；KTur为发电机的日启停次数；M为抽水蓄能电站机组最大启停次数。

2.3 抽水蓄能电站对于电网新能源消纳能力的提升分析

由于电力系统的电量平衡约束，且火电机组存在爬坡与调峰深度约束，所以新能源会发生发“弃风弃光”现象。弃电量的计算如下

(23)

式中，Sre为新能源弃电量；SPV为光伏弃电量；Swind为风电弃电量。

本文将风电、光伏与抽水蓄能协调后建立风-光-火-储联合调节系统，风-光-火-储联合调节系统的协调方式见图2。由图2可见在新能源高发阶段，抽水蓄能电站可以处于蓄能模式增加新能源的消纳；同时抽水蓄能可以在发电状态下，与新能源机组共同出力减轻火电机组出力负担。

同时抽水蓄能可以降低新能源机组出力的波动性使联合机组出力更加稳定，改善风电反调峰的情况，有利于火电机组响应新能源消纳[3，11-12]。

图2 新能源抽蓄联合机组协调方式

抽水蓄能电站具有一抽一发以及两抽两发的运行方式。本文拟在日负荷预测曲线分析的基础上分析，选择合适的运行方式，更好地提高抽水蓄能电站运行的经济性。

本文日负荷曲线预测按文献[13]方法确定，以图3的曲线为例。

图3 负荷预测曲线

为了判断每日负荷高峰低谷时段，将每天高于平均值的时段定义为高峰时段，低于平均值的时段定义为低谷时段。瞬时负荷值是否超过当日负荷的平均值判断结果逻辑值的情况如图4所示。

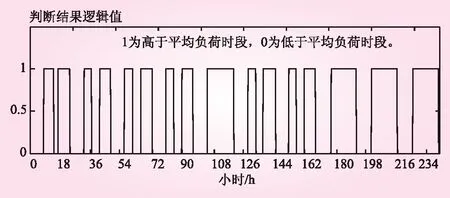
图4 负荷峰谷分布情况

图4中，1为高于平均负荷时段，0为低于平均负荷时段。

当出现较为明显的双高峰时宜采用两抽两发，反之则采用一抽一发的工作方式。建立抽水蓄能混合抽发概率模型，将双高峰中凹部与当日平均负荷作比较，建立概率策略模型，公式为

(24)

式中，K为采用何种工作方式的判断结果，当K=1时，采用两抽两发的工作模式；当K=0时，采用一抽一发的工作模式；Pav(i)为第i日的负荷平均值；φ为判读阈值，取值范围为(0，1)。

3 仿真及结果分析

以西北地区某风-光-火-储联合调节系统为例，应用本文所提出的抽水蓄能电站功率模型进行仿真分析。各类型电源装机容量如表1所示。本算例设置以15 min为时间精度，1天共计96个点，计算周期为10 d，分析并计算考虑天气条件对该系统运行的影响。设置3种工况条件进行对比分析。

表1 各机组参数

3.1 典型工况下的仿真

选择3种电网运行的典型工况。工况1：考虑抽水蓄能电站不出力时。工况2：考虑抽水蓄能电站出力但未考虑天气因素时。工况3：考虑抽水蓄能电站出力也考虑天气因素时。

3.2 计算结果

评价指标结果如表2所示。

表2 各工况评价指标结果

从表2可知，抽水蓄能电站可以有效地降低新能源的弃用，提新能源的利用率；在较为恶劣的天气条件下新能源的弃用率上升，运行成本上升，所以考虑天气因素建模对于抽水蓄能电站的使用效应评估与优化运行策略的提出有意义。

典型日仿真结果如图5所示，图5b、5c为两抽两发的工作模式。从图5可以看出，在考虑降水与蒸发对于抽水蓄能电站的影响时，该典型日过程中，由于抽水蓄能电站对于能量的存储与消纳，有效地提高了风电与光伏的消纳量；由于火电爬坡率的下降可以降低火电机组运行损伤，延长火电机组使用寿命，也间接带来了经济效益，从而提高了模型整体运行的经济性。