三峡升船机平衡重滑轮结构拓扑优化设计

汤伟毕，李 然，韩 伟，邹 涛

(长江三峡通航管理局，湖北宜昌443002)

0 引 言

三峡升船机为全平衡结构形式，船厢由256根直径d=74 mm的钢丝绳悬吊，钢丝绳分成16组对称布置在船厢两侧，钢丝绳的一端通过调节装置与船厢主纵梁外腹板上方的吊耳连接，另一端绕过塔柱顶部机房内的平衡滑轮与平衡重块连接，平衡重悬吊部分总质量为15 500 t[1]，平衡重滑轮采用焊接结构，由轮圈、大钢环、小钢环、辐板及轮毂等构件焊接而成，主材为Q345D，轮圈开设平衡重钢丝绳绳槽，大钢环开设安装钢丝绳绳槽(如图1)。滑轮的直径为5 000 mm，在加工制造过程中为分段拼接，滑轮两侧面是由若干块辐板结构件焊接而成，为保证其质量及精度，辐板焊接前需用工艺支撑块将其固定在大钢环与轮毂之间，在后期运行过程中出现部分支撑块焊接不牢而脱落，滑轮为双腹板结构，其内部为密封空腔，支撑块在滑轮空腔内碰撞异响。目前处理方式为在滑轮组特定位置开小孔，通过注入发泡剂对空腔内进行填充，限制支撑块与滑轮的相对运动，由于空腔内空间较大，开孔大小及开孔位置受限，发泡剂的填充效果不佳，处理异响情况不理想。

目前学者对滑轮的研究包括王瑞泽等[2]针对车载钻机天车轮进行轻量化设计、优化滑轮结构，王曾兰等[3]对大直径双辐板滑轮进行了设计及分析，钱仲庸和刘义等[4～5]研究了钢丝绳对滑轮的载荷分布以及滑轮组接触强度及承载特性，宋远卓[6]对滑轮进行了预应力模态分析及动态特性分析等。部分学者研究结构优化并确认了优化去材料的位置及大小，而利用拓扑优化方法针对大直径的滑轮结构的优化并指导去材料研究较少[7～8]。文中以三峡升船机平衡重滑轮结构为研究对象，针对现有滑轮腔体内存在支撑块脱落导致异响问题，对滑轮结构进行拓扑优化设计，其优化结果精确指导加工孔的位置和大小，取出支撑块。

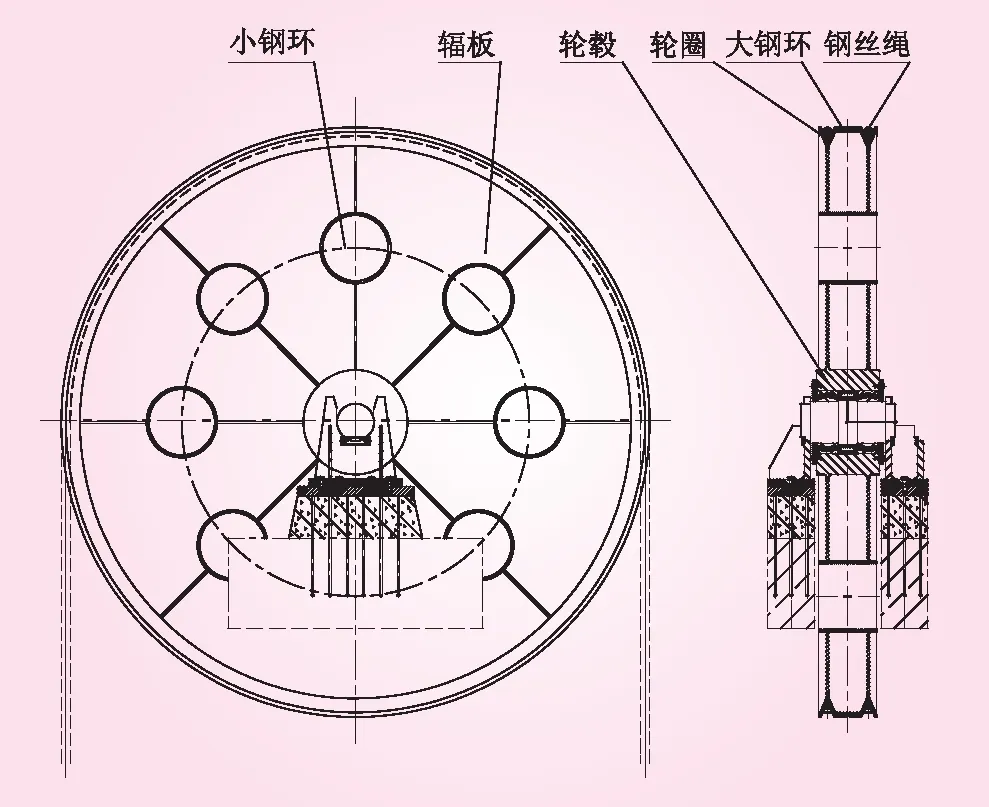
图1 滑轮结构示意

2 滑轮受力分析

该滑轮为目前国内升船机上直径最大的滑轮结构，文中对其结构优化的难点是减轻滑轮质量的同时如何保证滑轮的强度和刚度。考虑滑轮在静止或者匀速运动状态下所受的载荷情况，忽略因钢丝绳偏斜、自旋、绳内张力及摩擦力影响因素，其受力分布如图2，可知位于滑轮槽上钢丝绳两端所受的拉力为605.5 kN，得出钢丝绳对滑轮的作用力为正弦曲线分布，公式为

p(α，β)=p0sinαcosβ

(1)

式中，α为钢丝绳对滑轮作用力与水平方向的夹角，rad；β为钢丝绳径向线与竖直方向夹角，rad；p(α，β)为α和β弧度下钢丝绳对滑轮的作用力，kN；p0为α=π/2，β=0时滑轮的受力，kN。

p(α，β)在径向方向上的分量为p(α，β)sinα=p0sin2αcosβ，其合力为

(2)

式中，Ω为函数定义域；d为滑轮直径，mm；F为钢丝绳拉力，kN；b为滑轮槽接触的有效宽度，mm。

图2 滑轮受力分布示意

3 滑轮有限元分析

基于ANSYS软件主要对滑轮结构建立有限元模型进行静力学仿真分析，对模型中焊缝进行简化处理，选择SOLID186单元，选取滑轮结构材料为Q345D，其密度为ρ=7.85×10-9t/mm3，弹性模量E=2.06×105MPa，泊松比μ=0.3，对轮毂内圈施加全位移约束，对滑轮上半部分的轮槽施加载荷力p(α)=0.579sinαcosβ，通过分析得到的整体等效应力分布如图3所示，总位移如图4所示。

图3 滑轮等效应力云图

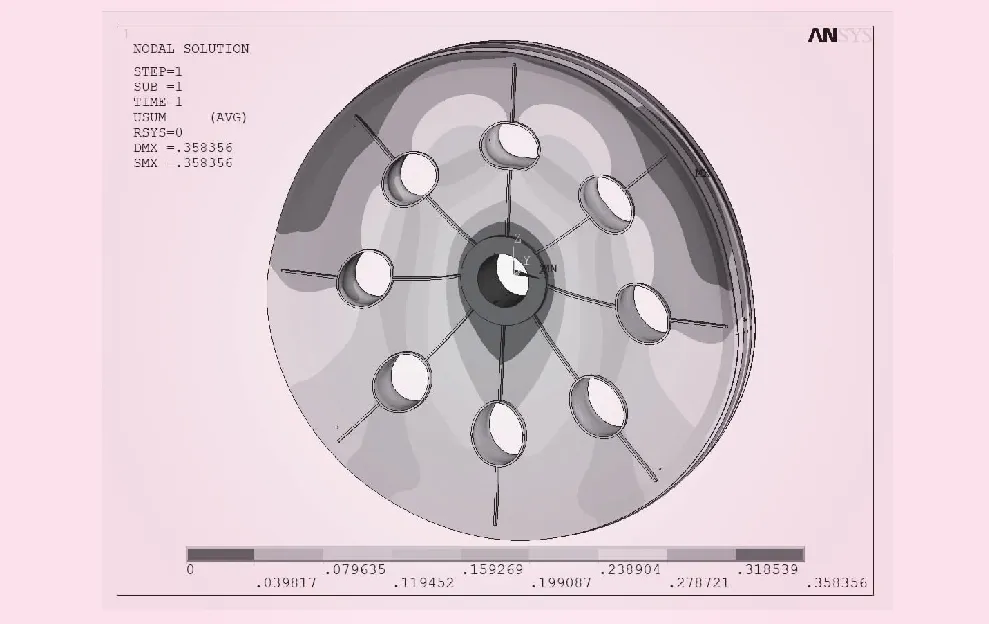
图4 滑轮总位移云图

从图3～4的仿真结果可知，滑轮所受的最大等效应力为95.3 MPa，其最大等效应力值主要集中在部分小钢环与辐板连接处以及轮毂与辐板连接处，其余大部分区域所受应力主要位于10.6～63.5 MPa区间；滑轮所受的最大位移为0.36 mm，其最大值主要集中在滑轮槽边缘附近区域。已知滑轮材料Q345D的屈服极限大于345 MPa，从其所受的等效应力和总位移综合分析，滑轮整体受力均衡，未出现应力集中情况，最大等效应力低于材料屈服极限值，位移变化值相对滑轮整体尺寸比值较小，滑轮结构强度较好，存在优化空间。

4 拓扑优化

4.1 拓扑优化理论

拓扑优化是一种在确定的结构空间中，通过施加约束条件和载荷作用下，搜寻结构内孔洞的大小、分布、形状及个数来减少材料的优化设计方法，目前拓扑优化技术主要的研究方法有均匀化方法、水平集法和变密度法等[9]。文中基于变密度法对滑轮组结构进行拓扑优化设计，变密度法是以结构体的单元密度为设计变量，以结构的柔度最小为优化目标，通过引入惩罚因子对单元密度进行离散处理，使单元密度向0或1两端集聚的方法，具体数学模型为

(3)

式中，C(x)为连续体的结构柔度目标函数；U为总位移矩阵；K为总刚度矩阵；ui为单元的位移矩阵；ki为单元的刚度矩阵；V(x)为有效体积约束函数；V0为初始状态体积；f为体积百分比系数；vi为第i单元的体积；xi为第i单元的设计变量，其中xmin为单元设计变量最小值，F为所受整体载荷矩阵。

4.2 滑轮组拓扑优化

文中以三峡升船机平衡重中滑轮为优化对象，基于ANSYS软件对其结构以柔度最小为优化目标进行拓扑优化，设置体积百分比系数为0.2，以滑轮每次转动1/8轮辐角度为基础施加8次多载荷载荷约束，模拟滑轮转动不同角度下的均匀受力工况，最终建立的拓扑优化模型如图5所示，图中设计区域为辐板，其他大钢环、小钢环和轮圈等为非设计区域，选定该设计区域的目的主要确定在辐板开孔的位置及大小，在保证滑轮满足强度要求的前提下通过开孔取出工艺铁块，从根本上消除滑轮异响情况。分析完成后提取密度大于0.8的优化单元如图6所示。

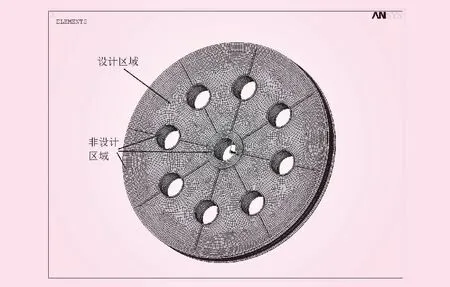
图5 滑轮拓扑优化模型

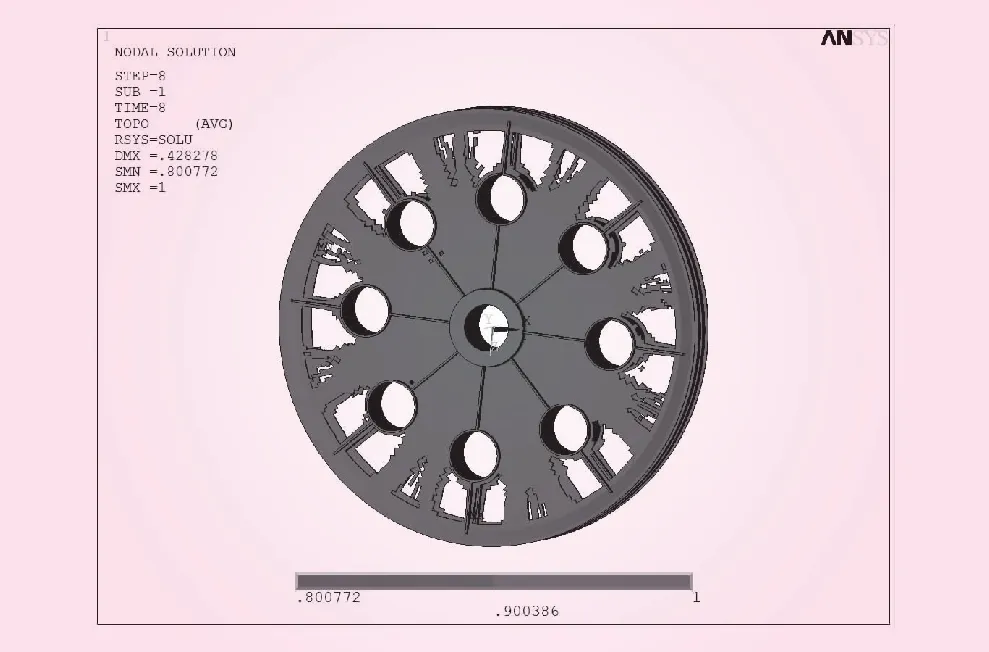
图6 拓扑优化结果

根据图6拓扑优化结果可知，辐板的主要受力区域在靠近轮毂中心区域，滑轮的整体受力情况均匀对称，减去的材料主要位于小钢环与轮圈之间的部分区域。通过分析得出滑轮结构减材料的区域可为其开孔的位置及大小提供参考。

5 模型重构及分析

已知滑轮结构拓扑优化结果中去材料的区域为不规则的孔洞，为方便取出腔体内的工艺铁块只需一个孔即可，考虑到滑轮的动平衡特性以及加工工艺的限制，在小钢环与轮圈之间的部分区域加工8组圆孔，取出铁块后在圆孔上焊接等直径的小钢环，最终优化重构的模型如图7所示。

图7 优化后重构模型

对优化后的滑轮模型重新进行静力学分析，约束条件和载荷施加与优化前模型一致，通过分析得到的整体等效应力分布见图8，总位移见图9。

图8 滑轮等效应力云图

图9 滑轮总位移云图

从图8～9中可知，滑轮所受的最大应力为81.2 MPa，其最大应力主要集中在部分小钢环与辐板连接处以及轮毂与辐板连接处，其余大部分区域所受应力主要位于9.1～63.2 MPa区间；滑轮所受的最大位移为0.33 mm，其最大值主要集中在滑轮槽边缘附近区域。

对比滑轮优化前后所受的等效应力和总位移情况可知：优化后的滑轮总重与优化前的比值为0.91；所受最大等效应力比值0.852；所受的最大应力区域相同，均位于小钢环与辐板连接处以及轮毂与辐板连接处，主要应力分布区间相似；优化后与优化前的最大总位移比值为0.94，均集中在滑轮槽边缘附近区域。

6 结 论

(1)对滑轮结构进行了理论受力分析，得出钢丝绳对滑轮的作用力为正弦曲线分布，基于ANSYS主要对滑轮结构建立有限元模型进行静力学仿真分析，可知滑轮结构强度较好，存在优化空间。

(2)对滑轮结构进行了拓扑优化，优化后在体积有所减少的情况下，最大应力和最大位移值均有所下降，重构模型得到最终结构，确定优化去材料部位和孔径的大小，在实际优化加工过程中取出滑轮腔体内支撑块，消除了异响。