基于滑模控制的双电机传动位置系统研究
2021-04-14丁飞,陈桂,周磊
丁 飞,陈 桂,周 磊
(南京工程学院自动化学院, 江苏 南京 211167)
随着科学技术的发展,高端装备制造公司对大型加工设备的适应性、生产效率和加工精度等提出了更高要求.受电机制造工艺限制,单电机驱动的传动系统不足以使大型加工设备正常运行.为了满足传动系统中大功率、高动态响应、高稳定性、高输出转矩的要求,多电机联合驱动成为实现传动系统要求的主要途径[1-2].在传动过程中,非线性变化的齿隙会使负载侧的速度和位移与期望值产生较大偏差,使传动性能降低[3].
为消除传动轮齿隙造成的位置跟随误差,一些学者进行了理论研究.文献[4]采用恒值偏置力矩对传动齿轮进行补偿,但齿隙呈现出的非线性变化使得每时每刻的齿隙补偿都不同,恒值偏置力矩不能很好地消除齿隙带来的传动误差;文献[5]采用PI控制作为位置控制器,在此基础上加上了齿隙补偿模块,通过调节控制器的参数,可在一定程度上减小位置误差.
由于滑模控制具有较强的鲁棒性,可在忽略齿隙、扰动的影响下,直接调节滑模面的参数来减小因齿隙造成的位置误差,因此本文在搭建双电机传动系统的基础上,用线性滑模函数和改进后的指数趋近律分别设计位置外环与速度内环的控制器,消除齿隙误差.通过Matlab/Simulink工具箱中的S-function模块编写相应算法,对比PI位置控制与滑模位置控制的仿真结果,验证控制算法的有效性.
1 双电机传动系统动力学模型
1.1 电机数学模型
直流电机电枢回路电压方程表达式为:
(1)
式中:ced为反电势系数;θd为电机转轴转角;Rd为电机电阻;Ld为电感;Id为电流.
直流电机的电磁力矩与电流成正比,电机电磁力矩的表达式为:
Td=KdId
(2)
式中:Td为电磁力矩;Kd为力矩系数.
在考虑电机转轴连接负载时,直流电机运动方程的表达式为:
(3)
式中:TL为负载力矩;Jd为电机的转动惯量;Bd为电机的粘滞摩擦系数.
1.2 传动齿轮数学模型
减速机与电机连接时,其转矩表达式为:
(4)
式中:Tj为减速机与电机转轴间的弹性力矩;ij为减速机内部的传动比.
电机转轴与减速机之间的转角关系为:
θd=ijθj
(5)
式中,θj为减速机对外输出转角.
电机转轴与减速机间的弹性力矩为:
(6)
式中:Jj为减速机转动惯量;Bj为粘摩系数;Tc为减速机与负载大齿轮间的弹性力矩.
减速机与负载大齿轮间的弹性力矩为:
Tc=Kc(θj-ifθf)
(7)
式中:Kc、if分别为减速机与负载大齿轮间的弹性系数、传动比;θf为大齿轮对外输出转角[6].
连接负载的大齿轮动力学表达式为:
(8)
将式(5)、式(6) 、式(7)带入式(4),得电机传动链动力学方程为:
(9)
对式(9)两边同乘传动比ij可得:
ijKdId
(10)
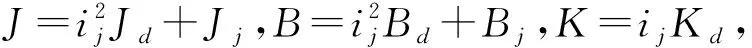
(11)
将式(5)代入式(1)可得:
(12)
联立式(7) 、式(8)、式(11)、式(12)可得双电机传动系统动力学模型:
(13)
将式(13)转换为复数域得:
(14)
齿隙死区模型是描述齿隙非线性的模型,见图1,该模型用相邻齿轮间的力矩变化表达齿隙非线性:

图1 齿隙死区模型
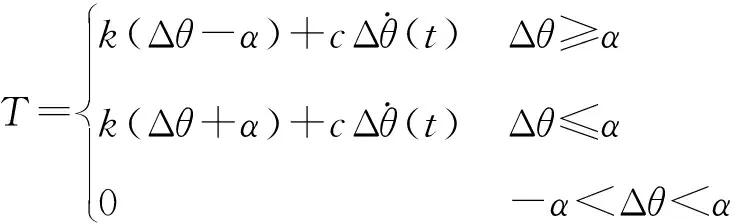
(15)
式中:Δθ(t)为相邻齿轮角度差,Δθ(t)=θ1(t)-θ2(t)/l,θ1(t)、θ2(t)为齿轮1和齿轮2的转动角度;k为传动系统刚度;α为齿轮1与齿轮2间的齿隙;c为阻尼系数;l为传动比.
当齿轮1处于两齿轮的齿隙宽度内,相邻齿轮无接触,作用力为0,当齿轮1转动角度超出两齿轮的齿隙范围时,相邻齿轮发生接触,产生作用力.结合式(14)和式(15)可得双电机传动系统结构图,如图2所示.分别在位置环与速度环添加对应的控制器,完成双电机传动的位置控制系统设计.
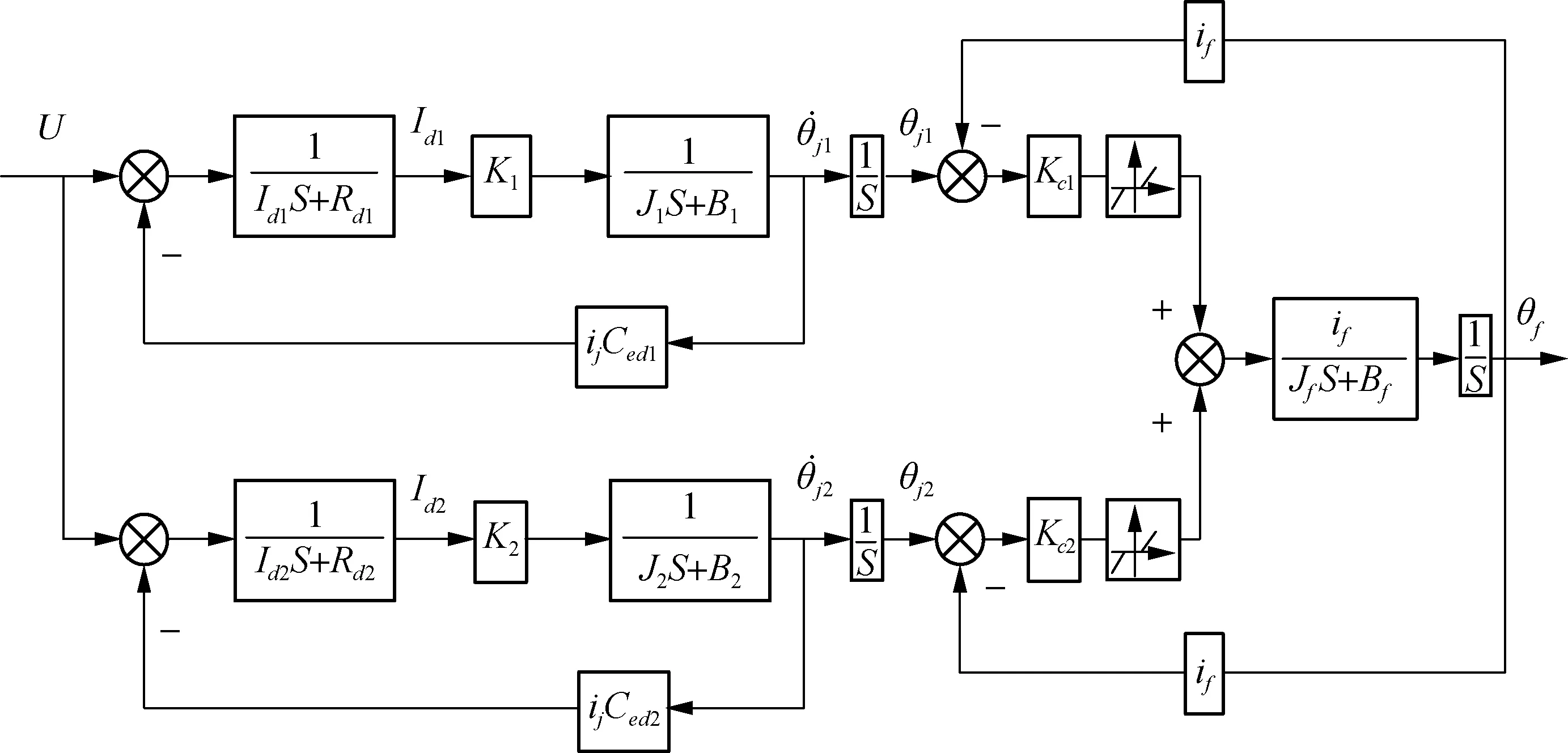
图2 双电机传动系统结构框图
2 滑模控制器设计
滑模变结构控制器的对外输出具有和开关相似的性质,使被控对象的输入量在+u与-u间不停切换的同时,整个控制系统也能快速趋于稳定[7].由于控制器的设计对被控对象的模型要求不高,使得在不能准确建立控制对象数学模型时,控制系统依然具有快速响应性与稳定性.当系统进入滑动模态后,控制器会对系统本身的干扰产生良好免疫特性,除了因控制器本身的切换输出量造成系统在稳定范围内的小幅抖振以外,基本不受模型参数和干扰的影响[8].
2.1 指数趋近律
原始的滑模控制会因输入量的不停切换产生抖振,且系统何时到达稳定无一致结论,可采用指数趋近律[9]来减弱抖振、提高稳定性,指数趋近律表达式:
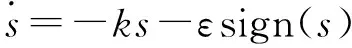
(16)
式中:k>0;ε>0;s为滑模函数;sign为符号函数,函数值为+1或-1.
通过调整指数趋近律中的k与ε,可以减弱控制信号的抖振,提高系统的抗干扰性.
2.2 滑模系统的稳定性
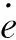
(17)
李雅普诺夫函数的导数表达式为:
(18)

2.3 位置滑模控制器
将位置误差及位置误差的微分作为状态量x1和状态量x2,其表达式为:
(19)
式中:θg为位置给定;θf负载末端的位置反馈[11].
将式(11)带入式(19),并对式(19)求导,得到系统的状态空间表达式:
(20)
根据传动系统模型建立滑模函数[12],位置滑模函数表达式为:
s=c1x1+x2
(21)
式中,c1为参数,且c1>0.
为了使控制系统在初始状态下就进入稳定状态、避免因被控对象建模不精准带来的影响,对传统意义上的指数趋近律进行改进,改进后的趋近律表达式为:
(22)

由式(2)与式(3)知,力矩与电流成正比.在忽略电机运动方程中的负载力矩与粘滞摩擦系数时,电磁力矩与电机转速成正比.综上所述,转速与电流成正比,表达式为:
Id=εwd
(23)
式中,ε为电气常数.
将式(20)代入式(22)可得滑模位置控制器的转矩输出表达式:
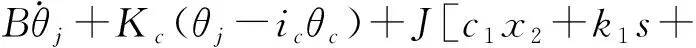
ε1sign(s)+2 000e-0.5tsign(s)]
(24)
将式(23)代入(24)得控制器的速度输出:
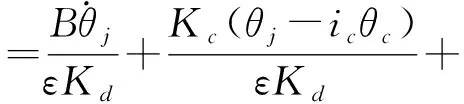
(25)
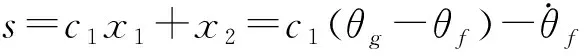
θf=θg-σ1e-c1t
(26)
式中,σ1为定值.
2.4 速度滑模控制器
将速度误差及速度误差的微分作为状态量x3和状态量x4,其表达式为:
(27)
式中:wg为速度给定;wf为电机末端速度反馈[14].
在负载力矩为固定值时,忽略负载力矩与电机粘摩系数,将式(2)、式(3)带入式(27),并求导,得到系统的状态空间表达式为:
(28)
根据传动系统模型建立速度滑模函数,其表达式为:
s=c2x3+x4
(29)
式中,c2为参数,且c2>0.
对式(29)求导,并与式(16)联立可得:
(30)
式中,k2>0,ε2>0.
将式(28)代入式(30)可得滑模速度控制器的输出微分量:
(31)
对式(31)进行积分,可得滑模速度控制器的输出电流:
(32)

wf=wg-σ2e-c2t
(33)
式中,σ2为定值.
3 传动系统仿真研究
传动系统中两电机规格相同,相关参数为:电机电阻Rd=0.5 Ω;电感Ld=0.015 L;电机反电动势系数ced=9.328 V·S/rad;电机力矩系数Kd=14.52 N·m/A;电机的转动惯量Jd=1.982 4 kg·m2;电机的粘滞摩擦系数Bd=0.89;减速机传动比ij=100;减速机与连接负载大齿轮间的弹性系数Kc=3 076 000 N·m/rad;传动轮间的齿隙为0.005 mm;减速机与负载大齿轮间的传动比if=5.11;负载的转动惯量Jf=41.2 kg·m2;负载粘滞摩擦系数Bf=0.05.
3.1 位置滑模控制仿真验证
为验证本文所提方法的有效性,分别对基于PID控制和滑模控制的双电机传动系统的位置控制进行仿真对比.真实的传动系统都会受到齿隙的影响,因此对于不同的给定信号,齿轮间隙这个非线性扰动一直都被添加在传动模型中,所给出的仿真结果也是建立在齿轮间隙这个扰动基础上的.分别给定仿真周期为5 s、幅值为1 rad的阶跃信号;7 rad/s的斜坡信号;周期为6.28 s、幅值为7 rad的正弦波信号.由图3可看出PID控制的位置阶跃响应时间约为0.3 s,滑模控制则为0.2 s;PID控制的位置响应曲线具有明显的超调波动,滑模控制则基本无超调,解决了位置跟踪中快速与稳定间的矛盾.图4中PID控制、滑模控制的位置阶跃误差控制分别在0.03、0.000 8 rad,滑模控制比PID控制的误差调节能力要好.图5中PID控制、滑模控制的位置斜坡响应时间分别约为0.7、0.15 s;滑模控制比PID控制的位置跟踪性能更好且无超调.图6中PID控制、滑模控制的位置斜坡跟踪误差分别稳定在0.17、0.135 rad左右;斜坡信号下滑模控制的与PID控制位置误差调节能力差别不大.图7中PID控制的位置正弦响应曲线与给定的正弦曲线相差太大,而滑模控制的位置正弦响应曲线则与给定正弦曲线基本重合,滑模位置控制器在正弦曲线下的追踪性能明显强于PID控制.图8表明PID控制无法进行精准的位置追踪,基于滑模控制的位置正
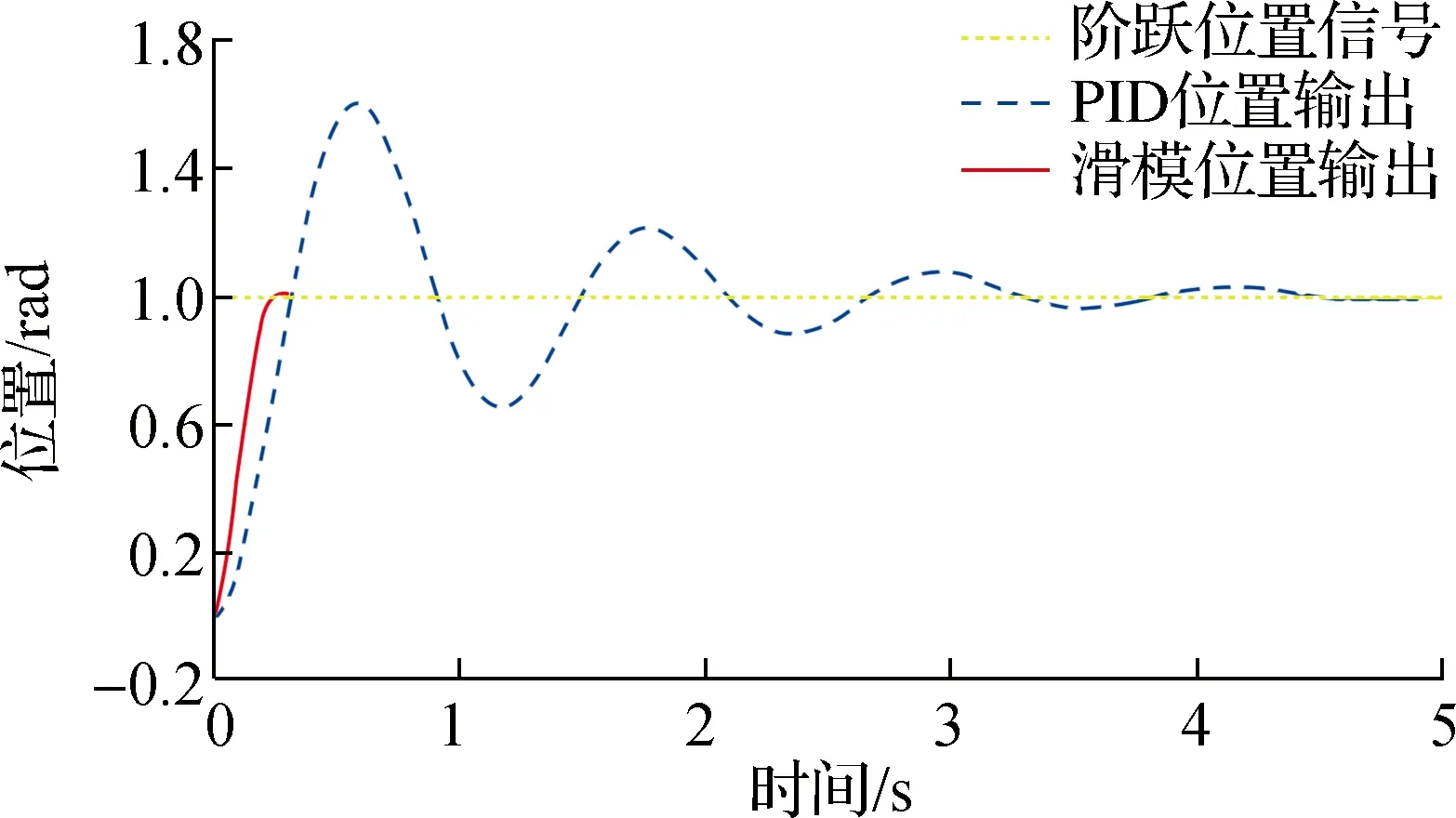
图3 阶跃信号下位置跟踪曲线
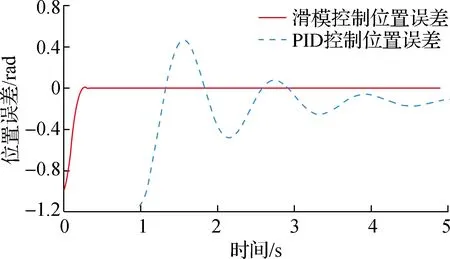
图4 阶跃信号下位置误差曲线

图5 斜坡信号下位置跟踪曲线

图6 斜坡信号下位置误差曲线

图7 正弦波信号下位置跟踪曲线

图8 正弦波信号下位置误差曲线
弦误差能稳定在0.3 rad,其误差调节能力明显好于PID控制.
3.2 速度滑模控制仿真验证
采用与位置滑模控制仿真相同的方法,分别对基于PID控制和滑模控制的双电机传动系统的速度控制进行仿真对比.速度仿真结果是建立在齿轮间隙扰动基础上的,三种速度给定信号的种类与幅值与位置仿真相同.图9中PID控制的速度阶跃响应时间约为滑模控制的3倍,两者的速度响应均无超调;图10中PID控制与滑模控制的速度阶跃误差基本相同,两者均稳定在0.005 rad/s;图11中PID控制与滑模控制的速度斜坡响应时间基本相同,约为0.15 s,两个控制器的速度响应性能相同;图12中PID控制的速度斜坡误差约为0.44 rad/s,滑模控制则为在0.21 rad/s,滑模控制的速度误差调节能力是PID控制的2倍;图13中PID控制的速度正弦响应曲线与给定速度信号的重合度远小于滑模控制,滑模控制速度控制器在正弦曲线下的追踪性能要强于PID控制;图14中PID控制速度

图9 阶跃信号下速度跟踪曲线

图10 阶跃信号下速度误差曲线
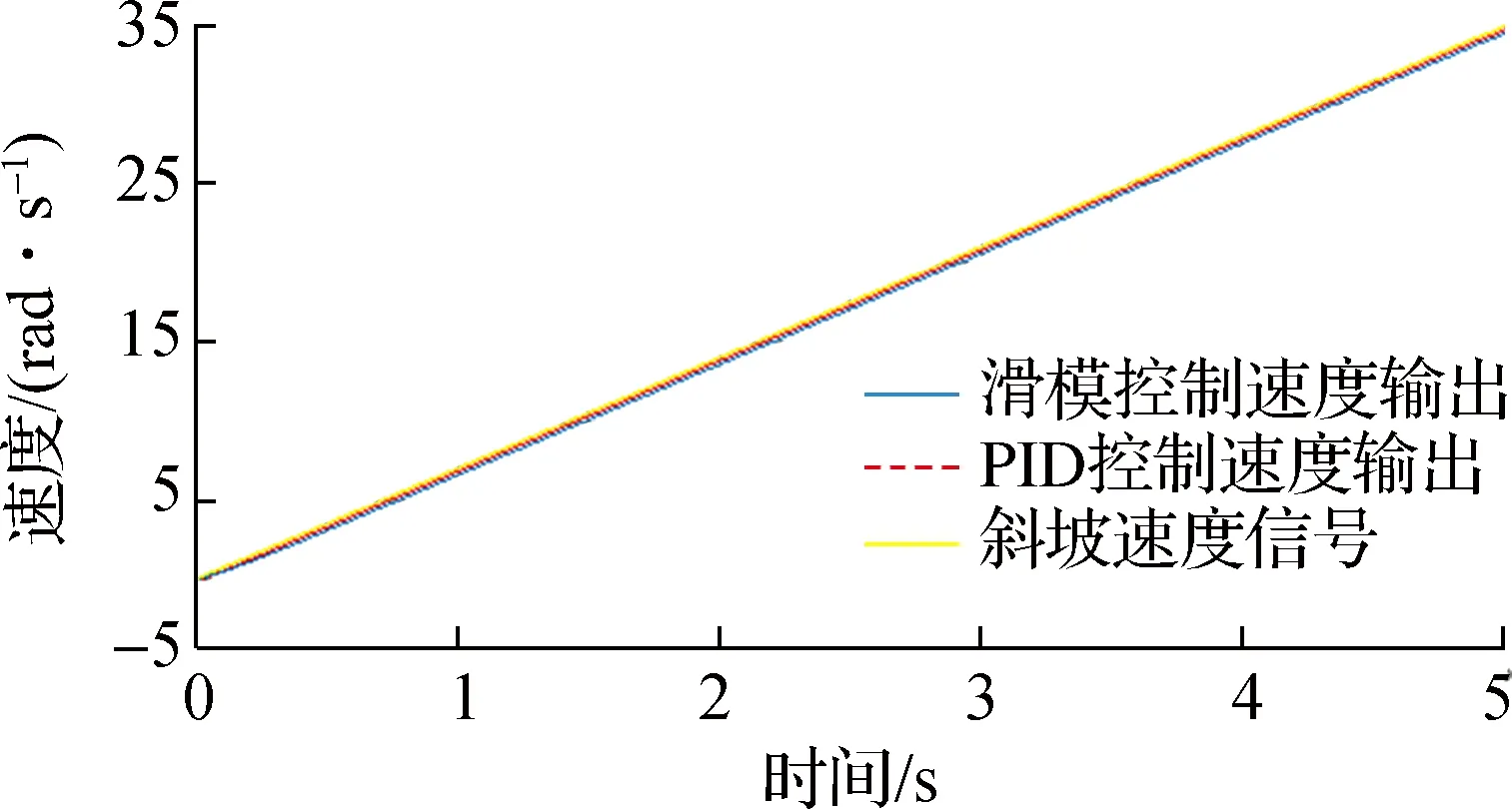
图11 斜坡信号下速度跟踪曲线
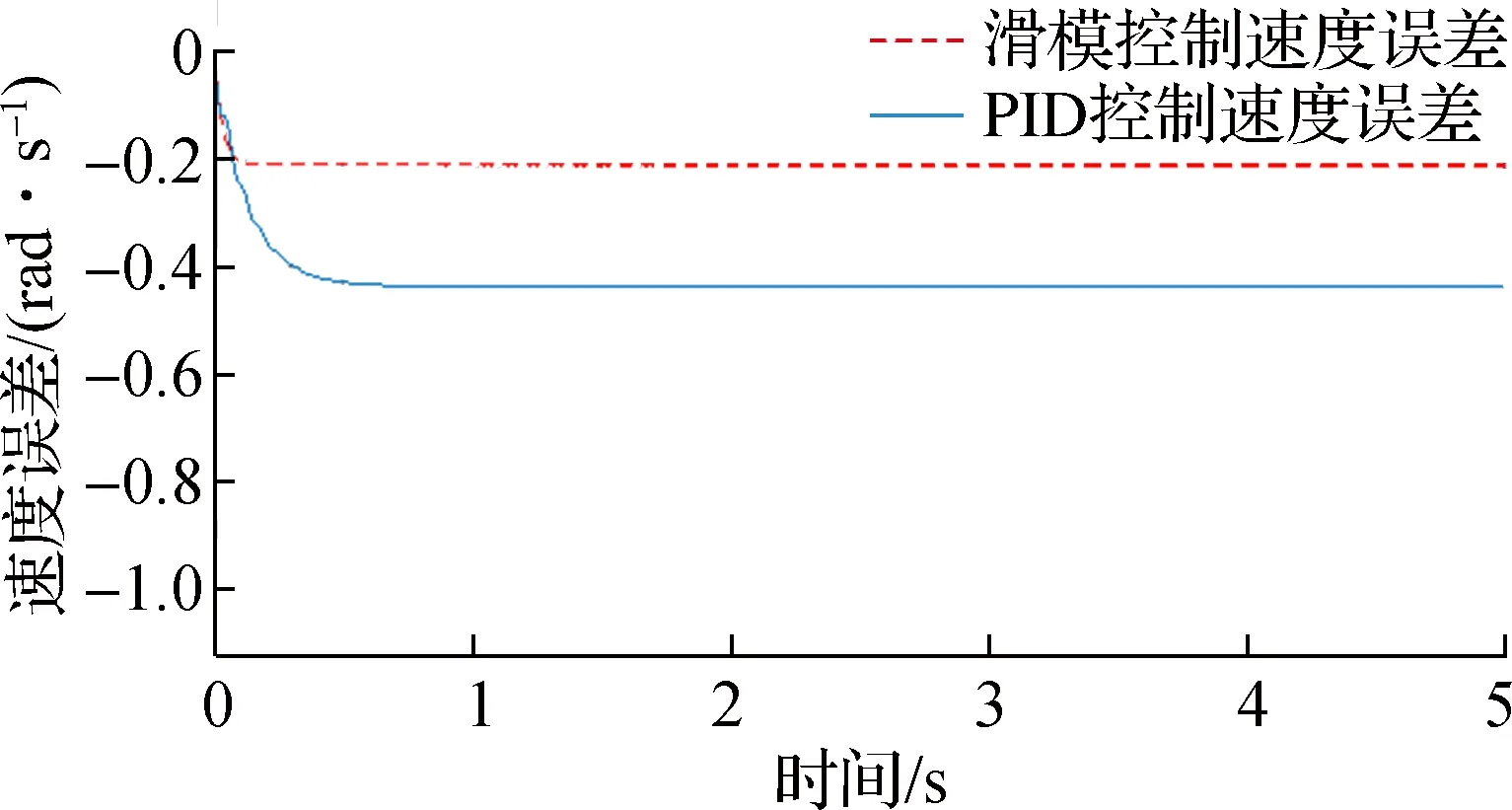
图12 斜坡信号下速度误差曲线
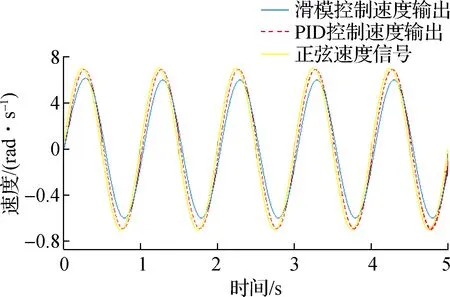
图13 正弦波信号下速度跟踪曲线
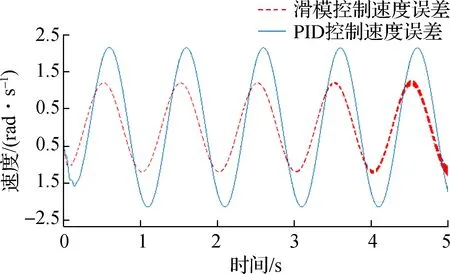
图14 正弦波信号下速度误差曲线
正弦误差在0~2.2 rad/s,滑模控制速度误差在0~1.2 rad/s,可看出滑模速度控制器的误差调节能力远优于PID控制.
4 结语
为克服齿轮间隙对双电机传动位置控制系统性能的影响,在搭建双电机传动系统数学模型的基础上,对系统的位置环和速度环分别进行设计并对其进行仿真.仿真结果表明,与经典PID控制相比,基于滑模的串级控制器可实现对给定信号的快速跟踪;在建立传动系统模型时,已将非线性的齿隙用死区模型来表示,在有齿隙模型的传动系统里,位置以及速度都可以实现对给定信号的快速追踪,这说明滑模变结构理论具有较强的鲁棒性,齿隙非线性扰动对滑模控制的影响较小;整个传动系统的动态调节时间远小于经典PID位置控制;基于滑模的位置控制可以满足传动系统的性能要求,能够减少齿隙对传动系统的影响.
