基于Adaptive Elastic Net与加速失效时间模型的亚组识别方法的应用拓展

韦红霞，康 佩，刘颖欣，黄福强，陈 征，安胜利

南方医科大学公共卫生学院生物统计学系，广东 广州510515

近年来，世界各地的监管机构和卫生技术评估机构越来越重视从试验（治疗）中识别获益的患者亚群，即亚组识别［1］；当传统临床随机对照试验中组间疗效无差异时，通过亚组识别，若能识别出实际上在试验组中存在明显获益的亚组人群，则可以有效减轻疾病对该亚组人群的危害［2］。目前，国内外亚组识别的研究已较多［3-5］，但涉及生存数据亚组识别的研究仍较少。现有生存数据亚组识别的研究，多是基于Cox模型［6-8］，而使用此模型需要满足等比例风险假定，但此假定有时不成立；对于高维的小样本数据，Cox模型也不够稳定。加速失效时间（AFT）模型已被证实适用于高删失和高维数据［9］，且无需满足等比例风险假定，因此可考虑将AFT模型作为Cox的替代模型。此外考虑到协变量之间的相关性问题，Engler和Li（2009）［10］提出了基于Elastic Net的惩罚AFT 模型。但Elastic Net 和其他惩罚模型（如lasso、岭回归）有一个共同的缺点：不能确保变量选择的一致性和系数估计的渐近正态性，即不具有Oracle性质［11］。针对此问题，Zou 和Zhang（2009）［12］提出了Adaptive Elastic Net。Khan&Shaw（2016）［13］也基于结合Adaptive Elastic Net的AFT模型，对高维数据进行变量选择。目前这些惩罚模型的应用局限于筛选协变量［9,10,13］，Kang（2019）［14］改进常规应用中的适应性正则化模型，将基于Adaptive Elastic Net的AFT模型应用于生存数据进行亚组识别，并探讨了其在不同的样本量、删失率、亚组比例下的性能。本文在Kang（2019）所研究的基础上进行拓展，进一步探讨协变量间相关性、获益亚组与非获益亚组间的疗效差异、样本量与待选协变量个数比例、生存数据的参数分布以及适应设计两个阶段的检验水准分配等对亚组识别的影响。

1 方法

生存数据亚组识别分析策略包括3个部分：亚组相关协变量筛选，亚组选择和临床效用性评价。

1.1 亚组相关协变量筛选

1.1.1 单变量AFT模型 假设临床试验中，包含一个试验组和一个对照组，且患者中存在两个亚组：获益亚组（g+）和非获益亚组（g-）。令p 表示待选协变量个数；n表示样本量；TR 表示组别变量（TR=0，对照组；TR=1，治疗组）；xij为第i 个患者的第j 个协变量；zij=xij·TRi为第i 个患者的第j 个协变量与组别变量的交互项；时间Ti=min(ti,ci)，其中ti和ci分别是出现终点事件和删失的时间；δi是第i 个患者的结局指示变量δi=I(ti≤ci)，当第i 个患者出现终点事件则δi=1，当第i个患者删失则δi=0。

为评估亚组之间治疗效果的异质性，对治疗和亚组之间交互作用进行检验是一种常用的统计方法。本研究中，拟合了单变量AFT模型；每次只纳入一个协变量xij、治疗变量TRi，以及交互效应zij：

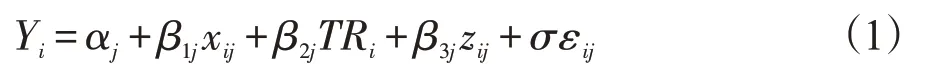
其中，Yi表示观察结局，Yi=log(Ti)，其中Ti是第i 个患者生存时间；σ 是尺度参数; εij是随机误差；β1j是协变量的回归系数；β2j是治疗变量的回归系数；β3j是协变量与治疗变量交互项的回归系数。若交互项有统计学意义，则xij为亚组相关协变量。

有研究表明同时纳入协变量xij与组别变量TR 主效应时，评估交互作用的效能往往较差［15-16］。因此，学者Freidlin 和Simon［17］提出了剔除协变量xij主效应的方法。本研究所对应的模型为：

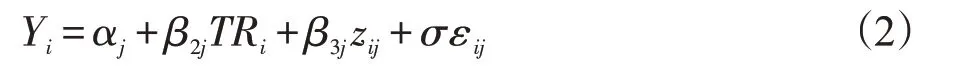
此外，若指定随机误差项εij的分布，则称为参数加速失效时间模型。若误差项服从标准正态分布、极值分布（尺度参数σ =1）、极值分布（尺度参数σ ≠1）、logistic分布，则分别对应着对数正态AFT模型、指数AFT模型、Weibull AFT模型、logistic AFT模型。Cox和Oakes（1984）［18］认为Weibull分布同时具有比例风险和加速失效时间的性质；Vanderhoef（1982）［19］和Scheme（2003）［20］、Sayehmir（2008）［21］等 学 者 的 研 究 表 明Weibull回归模型的拟合效果较好。因此本文的单变量AFT 模型考虑了Weibull 回归模型，即f( ε )=exp(ε-exp(ε))。

此处的单变量模型，通过Benjamini-Hochberg 算法控制错误发现率（false discovery rate，FDR）［22］，以实现多重校正。

记U={x1,x2,…,xk}为预先指定的错误发现率q=0.05 时，单变量AFT模型所筛选的亚组相关协变量的子集。

1.1.2 惩罚AFT模型 上述的单变量模型，模型每次只考虑一个协变量，没有考虑协变量之间的相关性问题；若建立多变量模型，则得到：

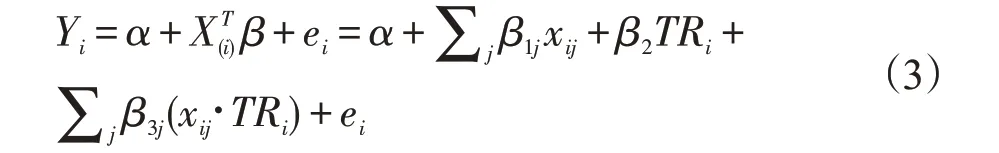
若在上式中剔除协变量xj主效应，则得到：

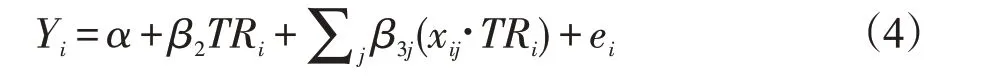
但是上述的两个模型通常只适合于协变量较少而样本量较多的数据；对于协变量数量超过样本量的数据，特别是高维的小样本（HDLSS）数据，常规模型不再适用。针对这个问题，Kang（2019）在上述模型参数求解 时 引 入 了Adaptive Elastic Net［14］。最 终Adaptive Elastic Net结合AFT模型的目标函数为：

1.2 亚组选择

亚组选择是指在患者人群中识别出对特定治疗手段有较好疗效的亚组人群g+。对于生存数据，其分为两步：首先基于上述模型所筛选的亚组相关协变量计算每个患者的预测得分；其次是寻找预测得分的截断点，把患者分成g+和g-两个亚组。采用Hinkley等［23］学者提出的change-point算法寻找截断点［24］。

1.3 临床效用性评价

亚组分析中，二阶段适应性设计常被用以评估治疗对亚组人群的有效性［25-26］。第一阶段，按检验水准α1，比较全部患者试验组和对照组的治疗效应；如果P ≤α1，则结论是治疗对全部患者有效；否则继续第二阶段，按α2，比较获益亚组人群g+中试验组和对照组的治疗效应；如果P ≤α2，则认为治疗对获益亚组人群g+有效（图1）。检验水准α=α1+α2（α 取值为0.05）。

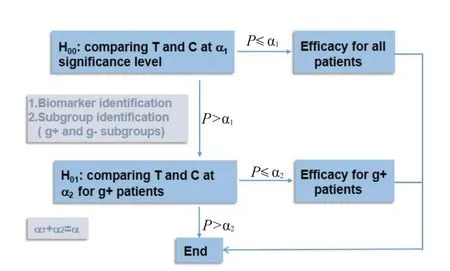
图1 二阶段适应性设计［14］Fig.1 Two-stage adaptive design[14].

2 模拟与实例

2.1 模拟

其中，截距β0，取值为2；σ 是度量参数，其取值为1；εi是随机误差，并假定其服从广义F-分布，例如Weibull分布、指数分布、对数正态分布、对数logistics分布、gamma分布等。根据前期研究［14］，得知回归系数β2取为3.2，β3j取-0.04。

记是否包含协变量主效应的公式分别为Eq_in、Eq_ex，考虑4种亚组相关协变量筛选模型：是否包含协变量主效应的单变量模型和惩罚模型，记为（“Univariate，Eq_in/Eq_ex”和“Penalized，Eq_in/Eq_ex”）。亚组选择分类器基于change-point算法。

存在亚组的条件下，模拟研究适应性设计的检验效能。每个数据集中，二阶段适应性设计中的第一阶段检验有统计学意义（P ＜α1），或第二阶段检验有统计学意义（P ＜α2），则适应性设计的检验效能记为1，否则记为0。通过模拟1000次，计算平均的检验效能。

各种情形设置如下：（1）设置低维、高维数据；分别产生样本量不超过协变量个数（n ≤p）、样本量远大于协变量个数（n ＞p）数据；其中，样本量不超过协变量个数（n ≤p）的数据中待选协变量个数p=600，样本量远大于协变量个数（n ＞p）的数据中p=100，亚组相关协变量个数k 均为10；（2）设置不同相关程度的协变量；亚组相关协变量间的相关性和非亚组相关协变量间的相关性设置为r=0、0.3、0.5；（3）调整适应性设计中两个阶段的检验水准α1和α2；由于所确定亚组治疗效果可能比整个研究人群大得多，因此在严格的显著性水准下对第二阶段的亚组进行分析仍可能具有较大的检验效能。所以考察了以下几种不同的组合（α1，α2）=（0.015，0.035），（0.02，0.03），（0.025，0.025），（0.03，0.02），（0.035，0.015），（0.04，0.01）；（4）在治疗仅对获益亚组g+有效(u00=u10=u01＜u11)的情况下，选取不同的回归系数β2和β3j的取值；其中，β2的取值越大，代表获益亚组与非获益亚组间的治疗效果差异越大；此处考察如下几种组合（β2，β3j）=（0.8，-0.01），（1.6，-0.02），（2.4，-0.03），（3.2，-0.04），（4.0，-0.05），（4.8，-0.06）；这几种组合下均是u00=u10=u01=2；当β1=0.8、1.6、2.4、3.2、4.0、4.8时，u11=2.2、2.4、2.6、2.8、3.0、3.2；（5）此前Kang的研究和以上研究中待选协变量个数为100和600，选取设置可能不够严谨、客观。本研究考虑待选协变量个数与样本量（n=400）的不同比例（0.25∶1,0.5∶1,1∶1,1.5∶1,2∶1,2.5∶1）下，模型的检验效能表现；（6）研究模拟产生生存时间的AFT模型的随机误差εi的不同分布（指数分布、极值分布、对数正态分布）对模型的影响。除了情形（3）以外，其他情形中α1=0.03、α2=0.02；（7）所有模拟设定样本量为400，删失率为30%，亚组比例为20%。

2.1.2 模拟结果 不同情形下模型在适应性设计中的检验效能如图2～4 所示。

由图2可知，图2A中随着协变量间相关性的提高，各模型的检验效能均呈平稳的状态。图2B中，适应性设计两个阶段的检验水准不同的组合（α1，α2）=（0.015，0.035），（0.02，0.03），（0.025，0.025），（0.03，0.02），（0.035，0.015），（0.04，0.01）下，不含协变量主效应的惩罚性AFT模型（Penalized，Eq_ex）的检验效能呈现平稳的状态，含主效应的单变量模型（Univariate，Eq_in）的检验效能呈现缓慢上升的状态；其他两个模型在α1取值为0.015～0.03时检验效能也是平稳的状态，但在α1取值为0.035时达到最高点，而在0.04时模型的检验效能下降8%左右。图2C 中，表现最好的也是“Penalized，Eq_in”与“Univariate，Eq_ex”。各个模型的检验效能随着回归系数β2的取值增大而增大；在n ＞p的数据中，当β2的取值为0.8～2.4 时，“Penalized，Eq_in”与“Univariate，Eq_ex”的检验效能较接近；而当β2的取值大于2.4时，“Univariate，Eq_ex”的检验效能高于“Penalized，Eq_in”。在n ≤p 的数据中，当β2的取值为0.8 和3.2 时，“Penalized，Eq_in”与“Univariate，Eq_ex”的检验效能较接近；而当β2的取值为1.6～2.4时，“Penalized，Eq_in”的检验效能高于“Univariate，Eq_ex”；而当β2的取值大于3.2时，“Univariate，Eq_ex”的检验效能高于“Penalized，Eq_in”。即，当β2的取值（获益亚组与非获益亚组间的治疗效果差异）较小时，“Penalized，Eq_in”较 有 优 势，其 他 情 况 下 则 是“Univariate，Eq_ex”的效果更好。

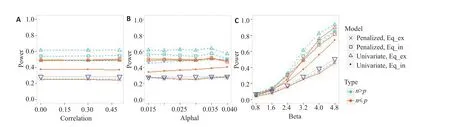
图2 不同情形下惩罚AFT模型在适应性设计的检验效能Fig.2 Power of AFT models in subgroup identification in different scenarios. In panel A, the correlation among covariates are set to be 0, 0.3, 0.5 respectively. In panel B, Alpha1 is the significance level α1 of the 1st stage of adaptive design.In panel C,Beta is the coefficient β2.

由图3可知，当待选协变量个数与样本量（n=400）的 比 例 为0.25∶1，0.5∶1，1∶1，1.5∶1，2∶1，2.5:1 时，“Penalized，Eq_ex”的检验效能较低且呈现平稳的趋势。其他三个模型的检验效能，在比例为0.25∶1，0.5∶1，1∶1时缓慢下降，下降了5%～10%；当比例为1.5∶1，2∶1，2.5∶1时，平缓下降。即样本量与待选协变量个数的比例不影响“Univariate，Eq_in”的检验效能，而其他三个模型的检验效能会随着比例的增加而缓慢下降；当比例小于1时，“Univariate，Eq_ex”的效能更高；其他情况下则是“Penalized，Eq_in”的效能更高。

由图4可知，相比于指数AFT模型产生生存数据时模型的检验效能，Weibull AFT模型产生数据时，各个模型的检验效能大幅下降至10%～20%左右。而对数正态AFT模型产生生存数据时，各个模型的检验效能都提高了，差距随着删失率的增大而增大；而且“Univariate,Eq_in”的检验效能超越了“Penalized,Eq_in”。其中，产生生存时间的模型类型对单变量模型的影响最大；对数正态AFT模型产生生存数据时，“Univariate,Eq_ex”的检验效能提高了0%～20%，而“Univariate,Eq_in”的检验效能提高了10%～25%，惩罚模型的效能提高了5%左右。产生生存数据的模型对单变量模型的影响较大，可能是因为单变量模型是参数模型，比较容易受到生存数据的参数分布的影响。

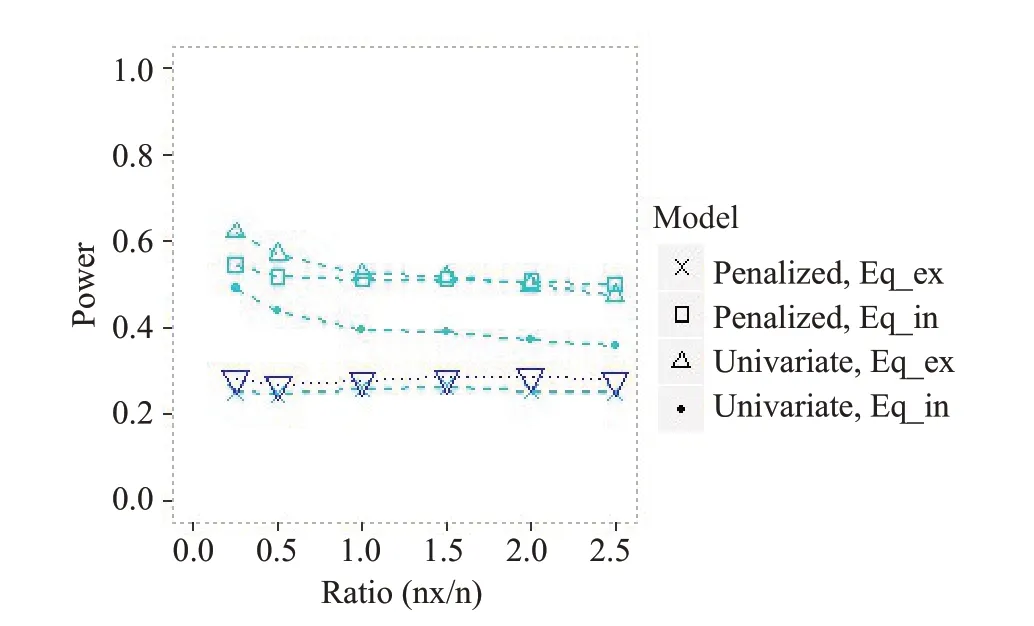
图3 不同的协变量个数下惩罚AFT模型在适应性设计的检验效能Fig.3 Power of penalized AFT model in subgroup identification in different number of sensitive covariates.Ratio is the ratio of the number of covariates to the sample size(0.25∶1,0.5∶1,1∶1,1.5∶1,2∶1,2.5∶1).The dotted line with inverted triangle (reference line)represents the powers of conventional design. The number of sensitive covariates is 10.

2.2 实例

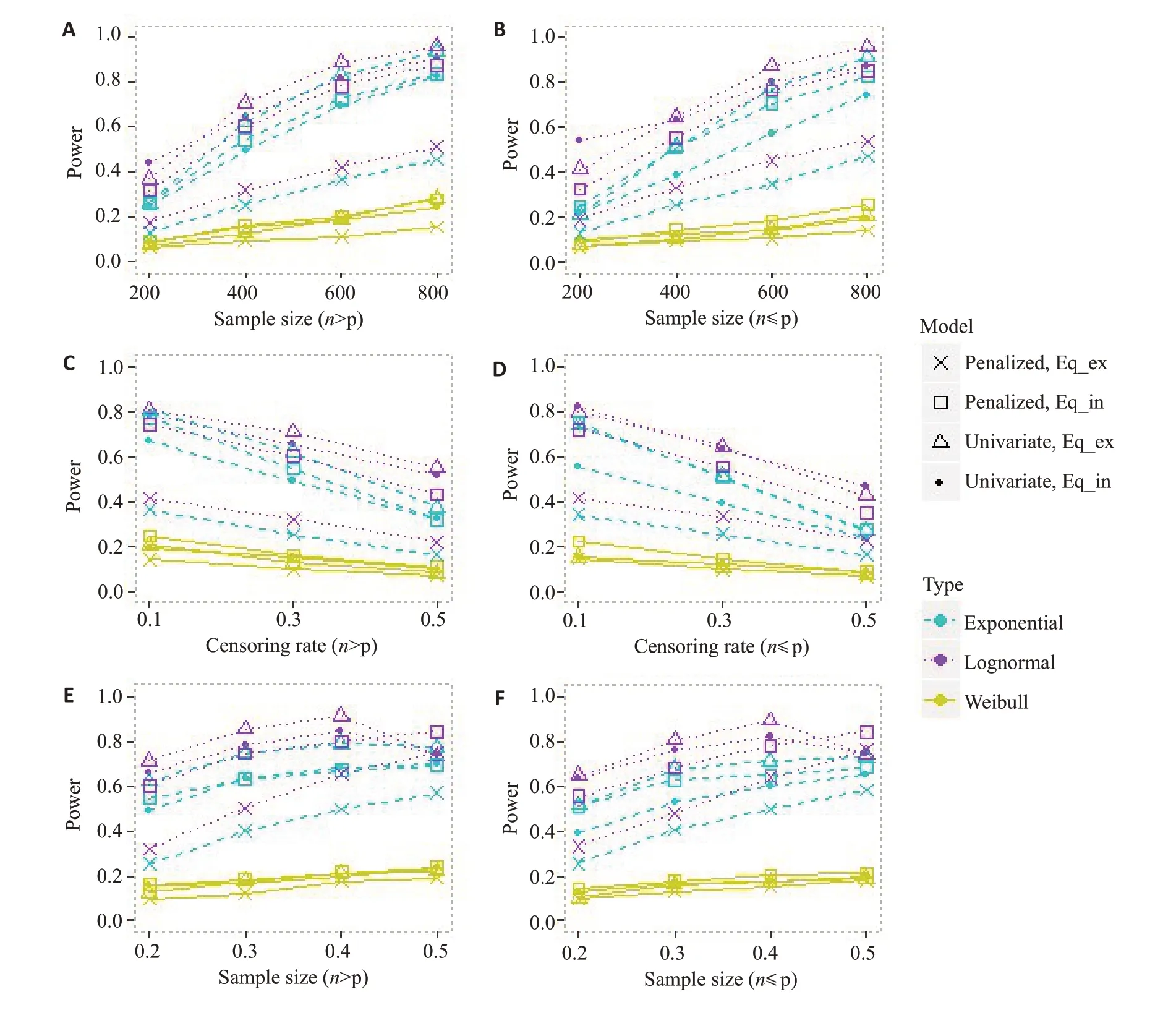
图4 生存时间参数分布不同时惩罚AFT模型在适应性设计的检验效能Fig.4 Power of penalized AFT model in subgroup identification when the parameter distribution of survival time differs. "Exponential" corresponds to exponential AFT model, and "Weibull"corresponds to WeibullAFT model,and"Lognormal"corresponds to lognormalAFT model.

数据来自艾滋病临床试验组175（ATCG 175）研究［27］。在这项研究中，2139名艾滋病毒感染者被随机分到4个不同的治疗组：齐多夫定（ZDV）单一疗法、ZDV+地达诺新（ddI）、ZDV+扎西他宾（zal）和ddI单一疗法。本研究选取联合用药组（ZDV+ddI）和单独用药组（ddI）的病人作为研究对象，两组病人的基线协变量均衡可比［31］。其中，有522名感染者接受了ZDV+ddI治疗，559人接受了ddI单一疗法。两组中的删失率分别是80.27%和77.10%。出现以下终点事件的时间作为观察结局：（i）CD4 T细胞计数至少下降50%；（ii）指示向艾滋病进展的事件；（iii）死亡。协变量包括患者的年龄和体质量、CD4和CD8计数、Karnofsky得分、先前接受抗逆转录病毒疗法的天数、是否患血友病、同性性行为、静脉注射吸毒史、研究前接受非齐多夫定抗逆转录病毒治疗、在治疗开始前30天内使用齐多夫定、在治疗开始前使用齐多夫定、种族、性别、抗逆转录病毒史、有无症状指标。前6个协变量为连续性变量，其他为二分类变量。

经检验满足比例风险假定（P=0.479），两组生存曲线比较选用log-rank方法，以及建立Cox模型计算风险比及其95%可信区间［28］。两组间生存曲线没有统计学差异（HR=0.84，P=0.181）（图5）［28］。

虽然尚不能认为ZDV+ddI组的治疗效果好于ddI组。但在ZDV+ddI组的病人中，可能存在获益亚组，因此考虑用不含协变量主效应的单变量模型（Univariate,Eq_ex）以及含协变量主效应的惩罚模型（Penalized,Eq_in），再结合十折交叉验证（10-fold cross validation）对该数据进行亚组分析，其中，单变量模型通过Benjamini-Hochberg 算法控制错误发现率（FDR）。

亚组识别结果如下所示。表1中，第3～4行展现了对照组与试验组的中位生存时间和组内样本量。适应性设计的第一阶段（α1=0.03）的结果（第1行）显示，对照组和试验组间生存时间没有统计学差异（P=0.181）；因此，继续适应设计的第二阶段分析（α2=0.02），结果（第2 行）显示：“Univariate, Eq_ex”和“Penalized,Eq_in”所识别的获益亚组中的两组间差异比较的P 值分别为0.369和0.549。图6、7给出了两个模型所识别的4个亚组的生存曲线图，结果显示试验组中获益人群（T+）和对照组中获益人群（C+）之间的治疗效果没有差异（图6），即两种疗法的获益人群相同，但“Univariate,Eq_ex”所识别的获益人群（T+和C+）的治疗效果显著优于非获益人群（T-和C-）（P＜0.001，图7）。其中，“Univariate,Eq_ex”和“Penalized,Eq_in”所识别的获益亚组分别为270+293=563 (52.08%)和141+183=324（29.97%）。

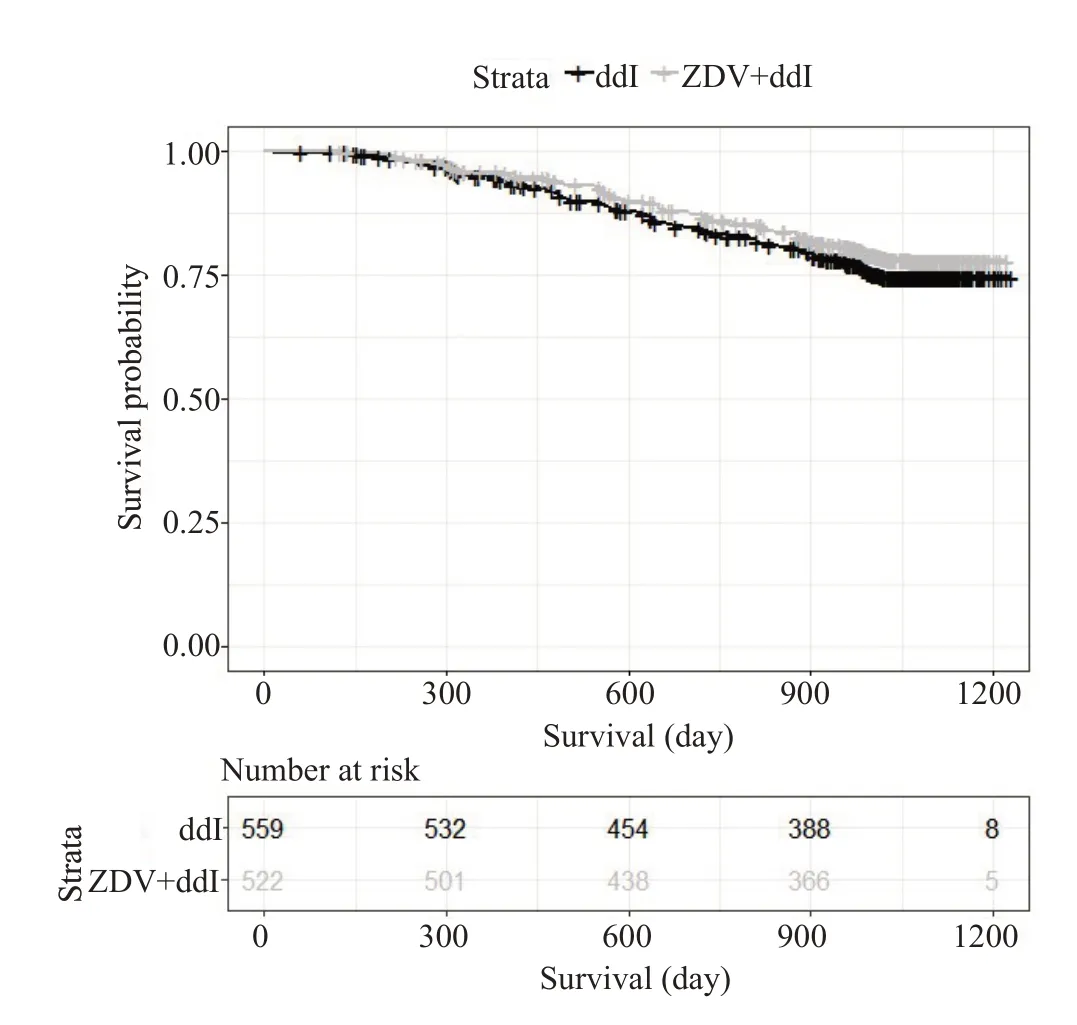
图5 两组间的生存曲线Fig.5 Survival curves of the ZDV+ddI group and ddI group.

表1 数据ACTG175的亚组识别结果Tab.1 Subgroup analysis of dataACTG175

3 讨论

目前Adaptive Elastic Net与AFT模型的结合主要应用于协变量筛选，Kang［14］的创新之处在于对其进行改进并应用于生存数据的亚组识别。本文在此基础上，进一步探讨了协变量间的相关性、获益亚组与非获益亚组间的治疗效果差异、样本量与待选协变量个数比例、生存数据的参数分布以及适应设计两个阶段的检验水准分配的影响。

对于样本量大于协变量个数（n ＞p）的数据，在n较小、删失率较高或者亚组比例较小等不利情况下，含主效应的惩罚模型在亚组选择上相对有优势；而其他情况下，则是不含主效应的单变量模型更优；对于n ≤p，含主效应的惩罚模型在亚组选择上相对有优势。此外，（0.035，0.015）可以作为二阶段适应形设计显着性水准的设置参考；协变量间的相关性不影响模型在适应性设计中的检验效能；生存数据的参数分布对单变量模型的影响较大，对惩罚模型的影响较小。获益亚组与非获益亚组间的治疗效果（对数生存时间log(T)）差异小于0.6（n ＞p 的数据中）或者小于0.8（n ≤p 的数据中）时，基于Eq_in的惩罚模型较有优势。

实例数据分析中，模型“Univariate,Eq_ex”的亚组识别结果显示，两种疗法的获益人群差异无统计学意义。另外，不管是接受联合用药还是单独用药，所识别的获益人群的治疗效果都优于非获益人群。这可能是由于该数据中样本量n 大于协变量个数p ，模型“Univariate,Eq_ex”的检验效能更高。

前期研究结果显示，在预先设定的检验水准（α1=0.03，α2=0.02）下，亚组选择中表现最好的模型在适应性设计中的检验效能并未显示出优势，提示这可能与两个阶段检验水准的设定有关。本研究发现，固定样本量（400），删失率（30%）和亚组比例（20%）时，（α1，α2）=（0.035，0.015）时亚组识别能力较好的两个模型（Univariate,Eq_ex、Penalized,Eq_in）的检验效能最高，但样本量、删失率和亚组比例等因素如何影响适应性设计检验水准的设置有待进一步研究。

当治疗有效且存在获益亚组时，我们仅模拟了治疗对获益亚组人群g+有效的情况(u00=u10=u01＜u11)；后续可拓展到治疗对获益亚组g+和非获益亚组g-都有效，但获益亚组g+的效果更好(u00=u10＜u01＜u11)的情形。另外，本研究提出的亚组识别方法仅限于识别两个亚组，即获益亚组和非获益亚组；后续可延伸到识别三个及以上亚组的情况。

Cox比例风险模型和AFT模型是分析生存数据最为常用的两种模型［28-29］，这两种模型潜在的假设是：在随访时间足够长的情况下，每个病人最终都将经历终点事件。然而，近年来，随着治疗效果的提高，临床试验中所收集到的生存数据常常存在被“治愈”的患者，即这部分患者（获益亚组）不可能发生相应的终点事件［28,30-32］。换言之，生存数据中患者的获益会存在两种情况，第一种是患者仅是生存时间延长了，最终仍会发生结局事件；第二种是患者治愈了，最终不会发生结局事件［33-36］。本研究仅考虑了第一种情况，对于第二种情况下疾病的治疗，我们更关注的不是生存时间的延长而是治愈率的提高，若仍然使用传统的Cox比例风险模型或者AFT模型进行分析，可能会得出不恰当的结论，因此后续拟将本研究所提出的分析策略拓展到潜在的亚组人群为治愈亚组的情形。

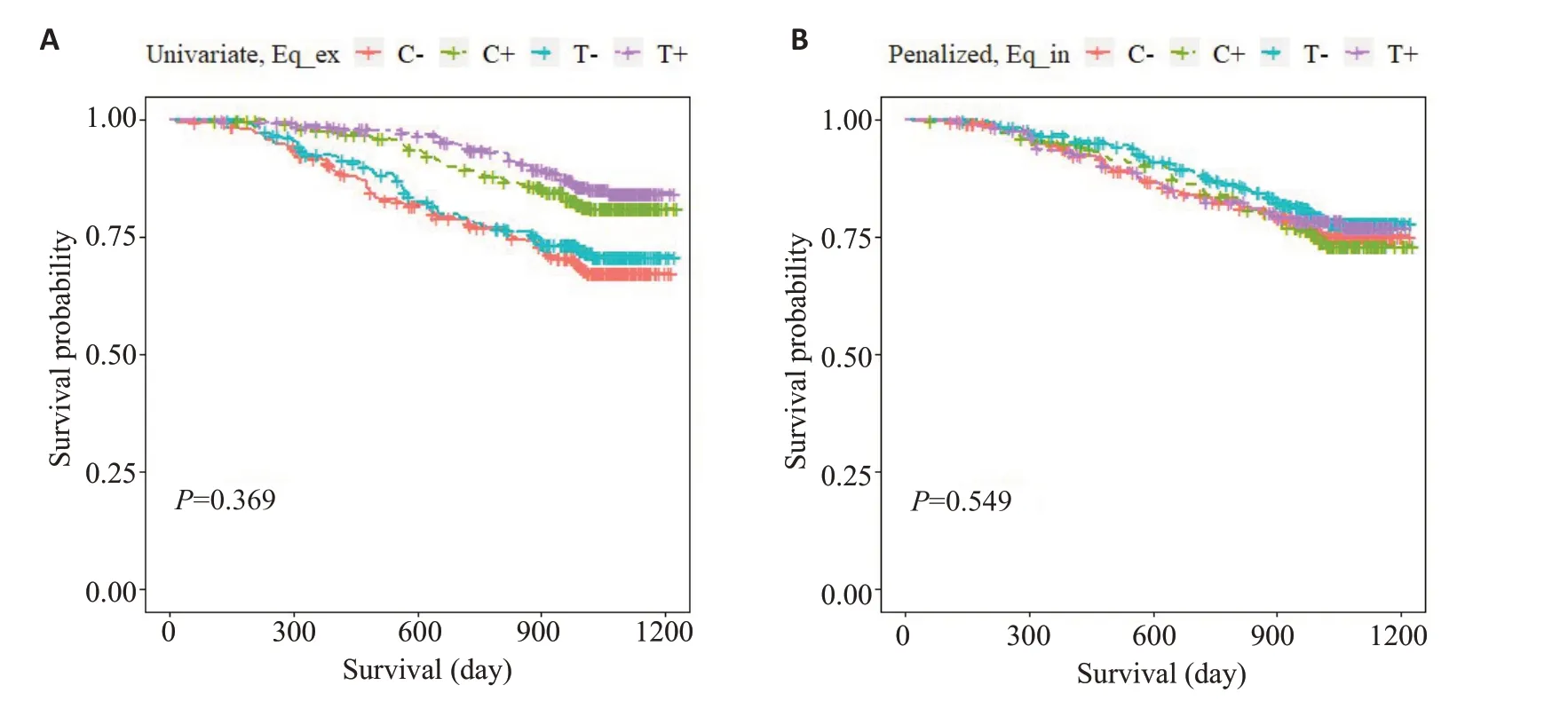
图6 四个亚组中不含协变量主效应的单变量AFT模型（A）、含协变量主效应的惩罚AFT模型（B）所识别的亚组生存曲线图Fig.6 Survival curves for subgroups identified by Univariate,Eq_ex(A),and Penalized,Eq_in(B).The four subgroups correspond to responder in ZDV+ddI group(T+),non-responder in ZDV+ddI group(T-),responder in ddI group(C+)and non-responder in ddI group(C-).

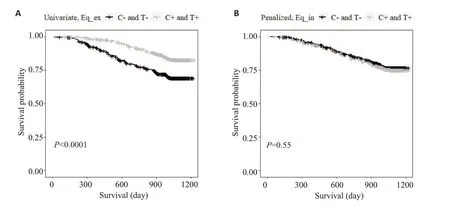
图7 两个亚组中不含协变量主效应的单变量AFT模型（A）、含协变量主效应的惩罚AFT模型（B）所识别的亚组生存曲线图Fig.7 Survival curves for 4 subgroups identified by Univariate,Eq_ex(A),and Penalized,Eq_in(B).The two subgroups correspond to responder in both arms(T+and C+),non-responder in in both arms(T-and C-).