耦合电感二次型高增益Boost 变换器

皇金锋，谢 锋，韩梦祺

（陕西理工大学电气工程学院，汉中723001）

随着能源危机的日益突出，新能源发电受到广泛关注[1-4]，在由光伏和燃料电池等构成的并网发电系统中，需采用高增益DC/DC 变换器。Boost 变换器具有升压能力，为获得高增益输出，须工作在极限占空比状态， 由此带来功率开关管电压应力大、输出二极管反向恢复损耗高及噪声严重等问题，故迫切需要对变换器拓扑进行改进，以提高其性能[5-8]。

为了提高Boost 变换器的电压增益， 国内外专家学者已经做了许多研究工作。 二次型Boost 变换器具有较高的电压增益[9-10]，但由于其是由级联Boost变换器演化而来， 因此功率开关管和功率二极管的电压应力较大， 并且存在输出二极管反向恢复严重等问题。其次，只能通过增加占空比以增大变换器的电压增益， 在需要较高电压增益的场合仍不能适用。耦合电感型Boost 变换器引入一个新的自由度（耦合电感匝数比），通过提高耦合电感的匝数比能显著提高变换器的增益， 近年来受到广泛关注[11-12]，但由于漏感的存在，在开关管关断时，开关管两端会产生较大的电压尖峰， 严重时甚至会击穿功率开关管，在实际应用中难以满足要求。

本文结合二次型Boost 变换器和耦合电感Boost 变换器的特点， 提出一种耦合电感二次型高增益Boost 变换器。 该变换器具有电压增益高的特点， 解决了二次型Boost 变换器开关管和输出二极管电压应力大以及耦合电感Boost 变换器开关管电压尖峰高的问题。通过合理设计变换器耦合电感的耦合系数，能够实现开关管的零电流开关和输出二极管的零电流关断，提高了变换器的工作效率。 实验结果验证了理论分析的正确性。

1 电路结构与工作原理分析

1.1 拓扑提出

本文提出一种耦合电感二次型高增益Boost 变换器，其变换器拓扑如图1 所示。 该变换器由三绕组耦合电感线圈NP、NS1和NS2，功率开关管Q，功率二极管Do、D1、D2、D3和D4， 电容C1、C2、C3和Co，以及负载电阻R 组成。 其中，D3、C2和NS1组成反激单元，D4、C3和NS2组成正激单元，根据文献[12]，可将正激单元和反激单元整合为桥式倍压单元，整合后的耦合电感二次型高增益Boost 变换器如图2 所示。 图3 为耦合电感二次型高增益Boost 变换器的等效电路，其中Lm为耦合电感的励磁电感，Lk为耦合电感的漏感。

由图3 可以看出， 当开关管关断时，C1能够吸收来自漏感Lk的能量， 避免Lk与开关管寄生电容发生谐振， 从而抑制了开关管Q 两端的电压尖峰，并且C1吸收的漏感能量可以放电至负载端， 实现了漏感能量的回收，提高了变换器的工作效率。D3、D4、C2和C3构成桥式倍压单元，二极管D3和D4交替导通， 将副边NS两端脉动较大的交流电压整流为直流电压，降低了输出二极管Do的电压应力。

图1 三绕组耦合电感二次型高增益Boost 变换器Fig. 1 Three-winding coupled-inductor quadratic high step-up Boost converter

图2 耦合电感二次型高增益Boost 变换器Fig. 2 Coupled-inductor quadratic high step-up Boost converter

图3 变换器等效电路Fig. 3 Equivalent circuit of the converter

1.2 变换器工作原理

在一个开关周期内， 变换器存在5 种工作模态，等效电路如图4 所示，工作波形如图5 所示。

工作模态1（t0～t1）：如图4（a）所示，t0时刻，开关管Q 开通，D1因承受反压而关断。电源Vi经回路Vi-Lm-D2-Vi为漏感Lk和励磁电感Lm充电， 由于漏感和励磁电感串联，等效电感量增加，抑制了开关管电流的上升率，近似实现了功率开关管的零电流开通ZCS（zero current switching-on）；电容C1经回路C1-L1-C1为L1充电； 副边线圈NS的电流正向减少 （规定流进同名端为电流的正方向），NS经回路NS-C2-D3-NS为C2供电；电容Co为负载R 供电。 此时流过原边线圈的电流为

图4 工作模态等效电路Fig. 4 Equivalent circuits in working modes

图5 变换器主要工作波形Fig. 5 Main working waveforms of the converter

工作模态2（t1～t2）：如图4（b）所示，t1时刻，D1因承受反压而关断。 副边线圈NS的电流正向下降到0，并反向增大，且经回路NS-D4-C3-NS为C3充电；电源Vi继续为Lk和Lm充电；电容C1为L1充电；电容Co为R 供电。 此时流过原边线圈的电流为

工作模态3（t2～t3）：如图4（c）所示，t2时刻，开关管Q 关断。 电源Vi经回路Vi-Lm-D1-L1-D3-D4-Do-R（Co）-Vi为R 供电； 漏感Lk中的能量经回路Lk-Lm-D1-C1-Vi-Lk向C1转移；L1经回路L1-D3-D4-Do-R（Co）-Vi-Lm-L1为R 供电； 电容C2经回路C2-NS-D4-Do-R（Co）-Vi-Lm-D1-L1-C2为R 供电； 副边线圈NS经回路NS-D4-C3-NS为C3充电。 此时流过原边线圈的电流为

工作模态4（t3～t4）：如图4（d）所示，t3时刻，开关管Q 关断，此时关断电流较小，可近似为零电流关断ZCS（zero current switching-off）。 副边线圈电流反向减小到0，同时正向增大，且经回路NS-C2-D3-NS为电容C2充电； 漏感Lk中的能量继续向C1转移；电源Vi继续经回路Vi-Lm-D1-L1-D3-D4-Do-R（Co）-Vi给Co和负载供电；电感L1经回路L1-D3-D4-Do-R（Co）-Vi-Lm-D1-L1为R 供电；C3经回路C3-Do-R（Co）-Vi-Lm-L1-D3-NS-C3为R 供电。 此时流过原边线圈的电流为

工作模态5（t4～t5）：如图4（e）所示，t4时刻，漏感Lk的能量被电容C1完全吸收。电容C1和电感L1串联经回路C1-L1-D3-D4-Do-R（Co）-C1为负载R 供电，从而实现了漏感能量的回收； 副边线圈NS的电流继续反向增大，经回路NS-C2-D3-NS为电容C2充电；C3经回路C3-Do-R（Co）-C1-L1-D3-NS-C3为负载R 供电。在t5时刻输出二极管近似实现了零电流关断ZCS。此阶段，原边线圈两端承受的电压为

式中，N 为耦合电感的匝数比，N=NS/NP。

因此流过原边线圈的电流为

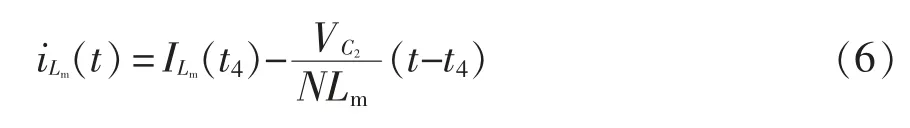
2 稳态分析

为简化分析，对变换器做如下假设：电容足够大，电容两端电压可视作恒值；所有功率器件均为理想器件；开关频率远大于其最大特征频率。

2.1 电压增益分析

设耦合电感的耦合系数k=Lk/（Lm+Lk），当开关管Q 开通时，由工作模态2 可得

当开关管Q 关断时，由工作模态3 可得

根据电感L1的伏秒平衡可得

将式（7）和式（8）代入式（9）可得

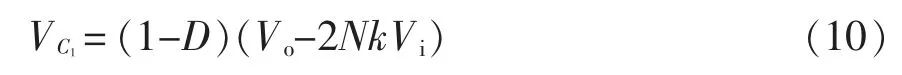
根据电感Lm的伏秒平衡可得

将式（7）、式（8）和式（10）代入式（11）可得变换器的输出电压增益为

式中，M=Vo/Vi。 分析式（12）可知，变换器的电压增益与占空比D、耦合电感匝数比N 以及耦合系数k有关，图6 给出了电压增益的三维曲线。

图6 不同耦合系数和占空比下的电压增益三维曲线Fig. 6 Three-dimensional curves of voltage gain with different coupling coefficients and different duty cycles

由图6 可知， 变换器的电压增益随占空比D、耦合电感匝数比N 和耦合系数k 的增加而增大。当耦合电感匝数比和占空比确定时，不同耦合系数对变换器电压增益的影响很小。 为了简化分析，可忽略漏感对变换器的影响，即取耦合系数k=1，此时变换器的电压增益为

2.2 电压应力分析

由工作模态1 可知， 输出二极管Do和二极管D4的电压应力为

由工作模态2 可知，二极管D1和二极管D3的电压应力为

由工作模态3 可知， 功率开关管Q 和二极管D2的电压应力为

将式（7）、式（10）和式（13）代入式（14）～式（16）中可得

分析式（17）可知，变换器全部功率器件的电压应力均低于输出电压， 可选取低耐压的功率器件，降低了变换器的成本。

3 性能对比分析

将二次型Boost 变换器和耦合电感Boost 变换器与本文提出的耦合电感二次型高增益Boost 变换器进行了性能对比分析，相关参数如表1 所示。

由表1 可知， 与二次型Boost 变换器和耦合电感Boost 变换器相比， 本文所提变换器不仅极大地提高了电压增益，而且显著减小了功率开关管和输出二级管的电压应力。

表1 不同变换器性能对比Tab. 1 Comparison of performance among different converters

4 参数设计

4.1 电感的设计

由于输入电流平均值Ii等于励磁电感电流平均值ILm，根据能量守恒可得电感电流平均值ILm和电感电流纹波ΔILm分别为

式中，f 为变换器的开关频率。

根据式（18）可得电感电流最小值为

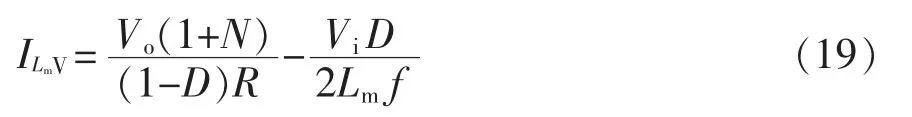
令ILmV=0， 则变换器工作于连续导电模式CCM（continuous conduction mode）时励磁电感应满足

4.2 电容设计

变换器应满足输出纹波电压要求。输出纹波电压由输出滤波电容决定，根据开关管开通时电荷守恒可得工作在CCM 时变换器的输出纹波电压为

因此，对于给定的输出电压纹波ΔVo，满足ΔVo的输出滤波电容Co的取值为

5 实验分析

为验证理论分析的正确性， 搭建了额定功率100 W 的实验样机，如图7 所示，电路参数见表2。

图7 实验样机Fig. 7 Experimental prototype

表2 变换器参数Tab. 2 Converter parameters

根据式（20）可得耦合电感为28 μH，取3.5 倍裕量得Lm=100 μH；根据式（22）可得输出滤波电容Co为7 μF，取3.5 倍裕量得输出滤波电容为25 μF。实验波形如图8～图12 所示。

图8 为输出电压波形，可以看出，20 V 的输入电压经高增益变换器， 得到了200 V 的输出电压。变换器的稳态占空比约为0.55，在实现高增益变换的同时避免了变换器工作在极限占空比状态。

图9 为耦合电感电流波形和漏感电流波形，可以看出，变换器工作在电感连续导电模式，并且漏感电流下降到0，这表明其能量被完全吸收，避免了开关管两端出现电压尖峰。

图10 为流过开关管Q 的电流波形及其两端的电压波形，可以看出，漏感的存在限制了电流变化率， 实现了功率开关管的零电流开通和零电流关断，提高了变换器的工作效率，且开关管的最大电压应力小于输出电压，可选取低耐压的功率开关管。

图8 Vi 和Vo 的波形Fig. 8 Waveforms of Vi and Vo

图9 VGS、iLm和iLk的波形Fig. 9 Waveforms of VGS, iLm and iLk

图10 VGS、IS 和VS 的波形Fig. 10 Waveforms of VGS, IS and VS

图11 VGS、IDo和VDo的波形Fig. 11 Waveforms of VGS, IDo and VDo

图11 为输出二极管的电流和电压波形，可以看出， 由于漏感的存在， 输出二极管实现了零电流关断，二极管的最大电压应力小于输出电压，可选取低耐压的功率二极管，实验结果与理论分析一致，验证了理论分析的正确性。 测得了耦合电感二次型高增益Boost 变换器的效率曲线，如图12 所示，可见，在额定输出功率下变换器效率达到了92%。

图12 效率曲线Fig. 12 Efficiency curve

6 结语

本文提出一种耦合电感二次型高增益Boost 变换器，该变换器结构简单，只存在一个功率开关管，控制难度小；全部功率器件的电压应力均低于输出电压，可选取低耐压、低寄生参数的功率器件，降低了变换器的成本；通过合理设计耦合电感的耦合系数，可实现功率开关管的零电流开关和输出二极管的零电流关断，有效解决了输出二极管的反向恢复问题，提高了变换器的工作效率。实验表明，该变换器能够适用于新能源发电系统。