基于菲波那切数列的病毒传播模型和在2019-nCoV 中的应用

蒋紫蔚＊ 喻翎馨

（南京市月华路小学，江苏 南京 210037）

0 引言

病毒传播模型能够描述传染病的流行和发展规律，有助于制定最优的防治策略。 2003 年非典以来，相继出现了禽流感、甲型H1N1 流感、H7N9 流感等一系列传染病爆发事件。 最近还爆发了2019-nCOV 病毒。自2019 年12 月在武汉发现第一批新型冠状病毒感染者以来，该病毒在短时间内在武汉以及国内其他省份中快速传播，并且在国外也很快出现了较多感染者。病毒的发展已经严重影响到了人们的日常工作与生活。 给全球经济和政治造成了巨大的冲击。 因而如何建立简单有效的病毒传播模型逐步进入公众视野，成为公共事件领域一个重要的研究课题。现存的传染病预[1-3]测模型主要包括SEIR 模型、时间序列模型、灰度预测模型、线性回归模型等。这些模型相对复杂，需要数学工具较多，并且除了SEIR 模型外，大多数模型并没有内在的预测逻辑。 菲波那切数列（Fibonacci sequence），又称黄金分割数列，由数学家莱昂纳多·菲波那切（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，在现代物理、准晶体结构、化学等领域，菲波那切数列都有直接的应用。病毒的传播也可以看作是一个病毒繁殖的过程。一个有趣的问题是，能否借助菲波那切数列的生成原理来构建一种简单有效的病毒传播模型？ 目前为止，还未发现有人做过此项研究。本文希望基于菲波那切数列的构成机制，建立一种病毒传播预测模型。

1 菲波那切数列与病毒传播模型

菲波那切数列以兔子繁殖为例子而引入，故又称为“兔子数列”。 数列的生成原理基于如下假设：

（1）第一个月初有一对刚诞生的兔子。

（2）第二个月之后（第三个月初）它们可以生育。

（3）每月每对可生育的兔子会诞生下一对新兔子。

（4）兔子永不死去。

这 样 形 成 一 个 数 列：1、1、2、3、5、8、13、21、34、……。 数列的后一项等于前两项之和。 病毒的传播也可以看成是病毒繁殖过程。 与“生兔子”类似，我们对病毒传播规律做如下假定：

（1）最初有n 例感染者。

（2） 新的感染者在感染初期不具备传染能力，在经过m 天后出现感染能力。 m 称为感染间隔天数。

（3） 每位感染者可以使k 位健康者变成感染者。k 称为感染再生数。

（4）最后只统计总的感染人数，不关心感染者死亡或者治愈。

基于上述假定即可建立病毒传播模型。 模型中，n、m、k 由实际情况确定。 需要指出：m 和k 反应的是一种统计平均效应，分别描述了病毒潜伏能力和感染能力。显然，n=1，m=1，k=1 时，模型预测的病毒感染总人数随天数的变化，就成为一个菲波那切数列。

2 数值结果

接下来， 将把我国2019-nCoV 确诊人数数据与模型预测数据进行对比。官方从2020 年1 月11 日开始公布数据， 为41 人 （参看http://www.nhc.gov.cn/;http://www.dxy.cn/）。 因此，本文选择初始感染人数m=41，为了计算方便，选取m=1，k=1。因此，除了初始“兔子数”不相同，模型的预测数据呈现的规律和菲波那切数列完全相同，即后一项是前两项之和。 官方检测数据在初期的几天变化并不明显，甚至在前四天确诊人数均没有变化 （参看http://www.nhc.gov.cn/; http://www.dxy.cn/），这可能是由于初期病毒检测存在延迟，以及检测面涉及不广的原因。 因此，前几日的官方数据可能并未体现病毒传播规律。 文章选择2020 年1月16 日的数据作为研究起点。模型也从2020 年1 月16 日开始计算， 官方公布数据和模型预测数据表格如表1 所示。

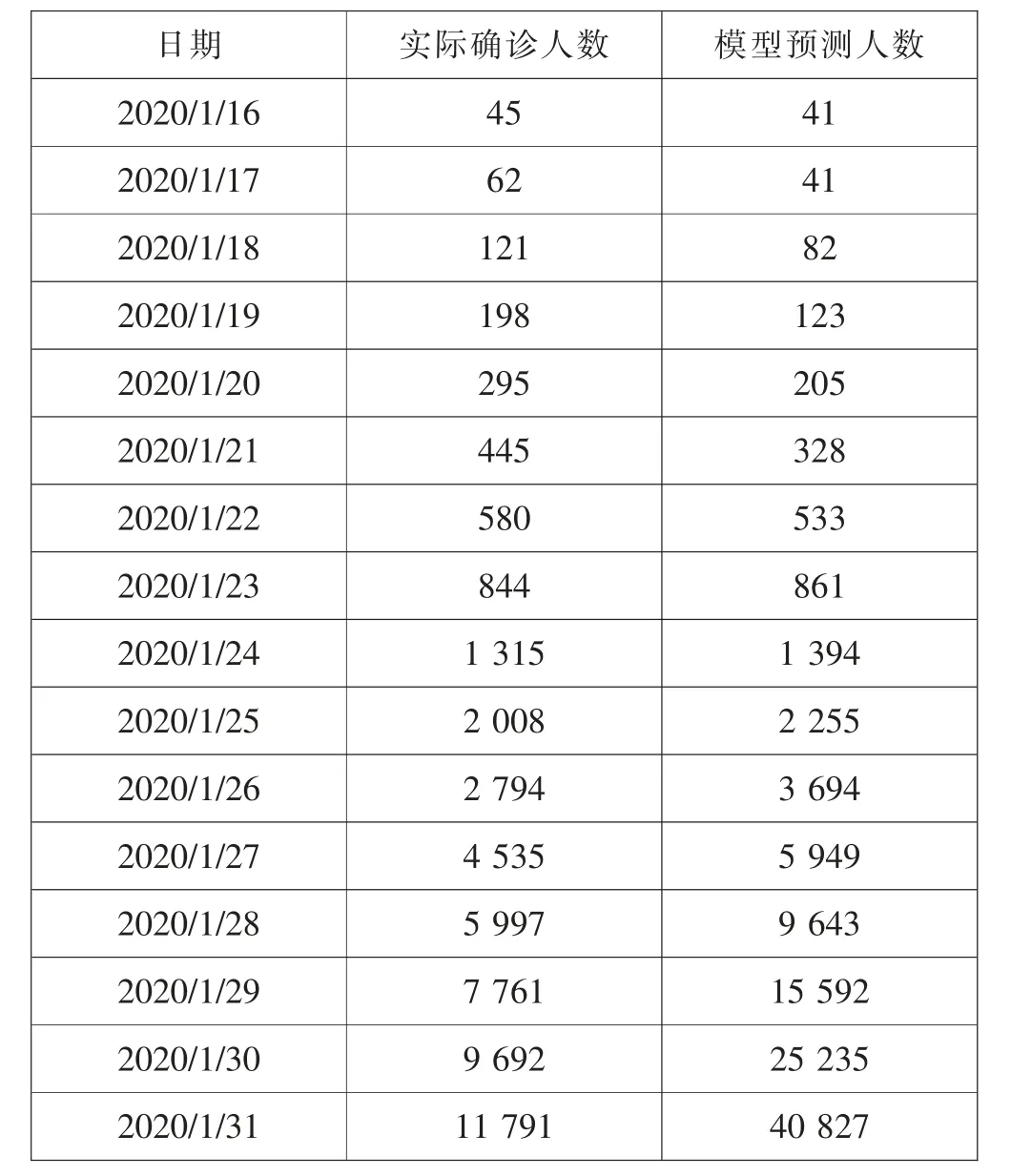
表1 官方公布的实际确诊人数和模型预测人数比较

从表中可以看到， 在2020 年1 月25 日之前，预测人数和实际确诊人数基本重合，这说明在病毒传播初期， 模型预测和病毒实际发展趋势符合较好。 从2020 年1 月26 日起，数据开始出现较大偏差。 这说明病毒传播趋势开始脱离原有发展轨道。 主要原因是，随着政府的管制加强、民众对病毒的认识加深，更多的民众选择佩戴口罩、防护设备以及选择居家少外出，这使得病毒感染趋势开始减缓。可以看到，如果按照病毒初期演变趋势，在2020 年1 月31 日，感染人数将达到40 827，而实际感染人数才11 791。 这也说明，我国采取的行政措施是及时有效的。

3 结论

文章基于菲波那切数列的生成原理构建了一种病毒传播模型。 在给出初始感染人数、感染间隔天数和感染再生数后，模型能够预测总的感染人数随时间的变化。 与2019-nCoV 的确诊数据进行比较，发现该模型在病毒传播初期的预测具有较高的准确性。模型的预测结果还表明我国在抗疫初期便采用了及时有效的行政干预，使得病毒传播趋势显著减缓。

菲波那切数列因为蕴含了普适的自然规律而被广泛应用于各学科领域。文章首次将菲波那切数列引入病毒传播领域，建立了一种简单有效的病毒传播模型。 由于引入的数学工具有限，该模型功能也较为有限， 暂时只能用于描述总的感染人数随时间的变化。然而，在病毒发展初期，医疗手段和资源有限，总的感染人数对于流行病毒评估具有重要意义。由于模型只引入了加法规律，该模型还为低年级数学教学提供了一份拓展案例。