颗粒沉降问题的高解析度CFD- DEM- IBM流固耦合数值模拟方法

2021-04-12底瑛棠赵兰浩

水科学进展 2021年2期

底瑛棠,赵兰浩,毛佳

(河海大学水利水电学院,江苏南京 210098)

颗粒沉降现象在自然界中普遍存在,具有广泛的工程应用背景,如泥沙运移[1]、血液流动[2]、气力输送[3]等。无论从工程应用价值或基础研究角度,颗粒与流体间的相互作用机理研究都意义重大。

颗粒沉降涉及颗粒间的碰撞及流固之间的双向强烈耦合,其高精度数值模拟目前仍极具挑战。描述颗粒两相流的数值方法主要有欧拉- 欧拉(Eulerian- Eulerian,E- E)方法[4- 5]和欧拉- 拉格朗日(Eulerian- Lagrangian,E- L)方法[6,8]。然而,E- E方法将流固两相视作可以相互渗透的连续介质,无法考虑颗粒的离散特性,实际更适用于固体呈现显著流态化特征的流动。为考虑颗粒的非连续性,张涛和李红文[6]基于E- L方法采用离散相模型(Discrete Phase Model,DPM)模拟了气固两相流管道内的孔板测量工况,将颗粒视作无体积的质点,通过牛顿第二定律描述颗粒运动。DPM模型假定颗粒相非常稀疏,忽略颗粒的相互作用,不考虑其对流体运动的影响,实则只是单向耦合,适用于固相体积分数小于10%～12%的情况[7]。针对稠密颗粒流,Hwang等[8]考虑了颗粒的体积效应与粒间碰撞及相间耦合,采用密集离散相模型(Dense Discrete Phase Model,DDPM)模拟了旋转分离器中的流动特性。但DDPM通过颗粒动力学理论计算颗粒间的相互作用,模化碰撞过程,并无清晰的物理碰撞面。

近年来,计算流体力学与离散单元法(Computational Fluid Dynamics- Discrete Element Method,CFD- DEM)因其处理颗粒碰撞问题的优势,被越来越多地用于颗粒两相流的研究。Yue等[9]基于CFD- DEM方法研究了喷动流化床中颗粒密度对喷流偏转的影响;杨文婧等[10]采用CFD- DEM方法对固体火箭发动机中气固两相流进行了数值模拟。CFD- DEM方法能够考虑两相之间的耦合作用,引入颗粒接触模型描述颗粒的物理碰撞过程,并通过空隙率考虑颗粒的体积效应,是求解颗粒两相流宏观特性的极佳选择。然而,传统的CFD- DEM方法通过经验公式计算两相间的耦合作用力[11],称作非解析的CFD- DEM方法。由于缺乏对颗粒边界的描述,颗粒周围的流场信息无法得到精确解析,从而无法描述颗粒的尾流效应[12],决定了该方法只适用于颗粒间无干扰的稀疏颗粒两相流问题。

为解决目前非解析CFD- DEM方法的弊端,准确求解流固耦合作用力,获得解析的流场,主要的难点在于流固运动界面的描述。传统的动网格方法[13]需要在每个时间步内更新计算域网格,考虑到颗粒沉降运动过程中的大位移,采用贴体动网格方法处理颗粒的运动边界计算成本较高,并可能产生网格扭曲等问题。Peskin[14]提出的浸入边界法(IBM)采用固定的结构化网格,在固体边界上覆盖拉格朗日点以追踪其运动边界,回避了动网格方法的缺陷。通过在Navier- Stokes动量方程中附加体力项来实现固体边界对流场的影响,浸入边界法不仅无需实时更新网格,节省了网格生成所需的时间,也无需处理从物理平面到计算平面的坐标和网格的转换问题,正逐步被应用到更广泛的工程领域[15],对于稠密颗粒系统的沉降这种动态边界问题尤为适用。

本文基于CFD- DEM和IBM方法提出一种高解析度CFD- DEM- IBM流固耦合数值分析方法,基于自主开发的程序开展颗粒沉降问题的数值模拟研究,通过与前人工作的对比验证了该方法能够描述颗粒的实际边界,获得完全解析的流场,从而能够考虑颗粒尾涡结构的影响,为深入了解颗粒两相流运动特性提供了有力工具。

1 数值方法

1.1 流体控制方程

连续的流体相由黏性不可压缩的Navier- Stokes方程作为控制方程,为考虑颗粒边界的影响,在动量方程的右端附加额外的体力项:

·un+θ1=0

(1)

(2)

式中:u为速度；t为时间；ρ为密度；p为压力；τ=μ(u+Tu)为黏性应力张量,μ为动力黏度；fb为体力项；f为附加体力项,表示固体边界对流体的作用力；n为时间步；θ1和θ2的取值范围均为[0,1],时间离散格式当0.5≤θ1≤1且θ2=0时为显式,当0.5≤θ1≤1且0.5≤θ2≤1时为半隐式格式。

1.2 固体控制方程

固体的运动由牛顿第二运动方程控制:

(3)

(4)

式(3)中,接触力包括法向接触力Fcn和切向接触力Fct,分别由下式计算得出:

(Fcn)i=(Fcn)i-1+ΔFcn

(5)

(Fct)i=(Fct)i-1+ΔFct

(6)

式中:下标i表示ti时刻;Δt=ti-ti-1为时间步;力的增量满足ΔFcn=knδn+ηnGn及ΔFct=ktδt+ηtGt;k为刚度系数；δ为接触点的相对位移增量；η为阻尼系数；G为接触颗粒的相对速度;下标n和t分别表示法向和切向分量,其中切向力应当满足库仑摩擦定律(Fct)max=Fcn·μc,(Fct)max为最大允许静摩擦力,μc为摩擦系数。

流体对颗粒的作用力Ff为施加于浸入边界点上的力,与作用于流体网格点上的附加体力项f含义不同。Ff可由参考文献[16]计算得到:

(7)

式中:Ω为固体边界SP外、计算域边界Sout内的流体域；Ω′为整个计算域；Ω″为SP所围固体域,如图1所示。

图1 颗粒沉降问题的CFD- DEM- IBM方法示意

1.3 浸入边界法

为处理颗粒的移动边界,引入直接力浸入边界法[17],如图1所示。浸入边界法采用基于欧拉框架的正交笛卡尔网格离散整个计算域,并在颗粒的物理边界上布置浸入边界点,流体网格点与浸入边界点之间的信息传递通过插值函数I与分布函数D完成。

将动量方程式(2)沿特征线展开可得到时间离散后的动量方程:

un+1=un+Kn+Rn+θ2+fn+1Δt

(8)

fn+1Δt=D[Vn+1-I(un+Kn+Rn+θ2)]

(9)

1.4 数值求解方案

1.4.1 流体相的迭代求解

由式(9)可见,流体的速度、压力与附加体力项相互耦合,需要采用迭代方案求解流场。根据分步投影法,定义不包含压力项与附加体力项的中间速度场u*,k=un+Kn,流场的求解过程如图2所示。

图2 流体域迭代求解步骤

其中,内循环中附加体力项根据下式求解:

fn+1,k,iΔt=fn+1,k,i-1Δt+D[Vn+1-I(un+Kn+Rn+θ2+fn+1,k,i-1Δt)]

(10)

内循环的收敛判断则依据为‖Vn+1-I(un+Kn+Rn+θ2+fn+1,k,i-1Δt)‖<ε,其中‖·‖为任一范数,容差ε取为1×10-5。外循环的收敛判断依据为‖I(un+Kn+Rn+θ2,k)-I(un+Kn+Rn+θ2,k-1)‖<ε。如图2所示,采用迭代的方式隐式求解附加体力项,在保持流体的速度、压力与附加体力项相互耦合的同时,满足无滑移边界条件,并在附加体力与压力项的迭代计算内进行速度校正,确保结果满足散度自由。

1.4.2 流固耦合系统的迭代求解

颗粒与流体间存在双向相互作用,形成强流固耦合系统,采用分区方案求解分属不同控制方程的流固两相。根据标准Galerkin加权余量法进行空间离散,流固两相的控制方程迭代格式可记作:

(Δun,k,Δpn,k)=RHSf(un,pn,δn+1,k-1)

(11)

Δδn,k=RHSs(δn,un+1,k,pn+1,k)

(12)

式中:RHSf与RHSs分别为流体方程与固体方程的右端项。

现假设第n步计算已完成,依据以下流程展开第n+1步的第k次迭代:

(1) 求解流体方程式(11),更新速度场un+1,k及压力场pn+1,k；

(2) 求解固体方程式(12),更新固体位置δn+1,k；

(3) 计算‖Δζn,k-Δζn,k-1‖判断收敛,若小于容差εζ,则满足收敛条件,结束当前时间步的计算,否则令k=k+1,重复(1)—(3)直至满足收敛条件。式中ζ可取为变量u、p或位移δ,εζ取为1×10-5。

2 数值算例

为验证本文方法的准确性与有效性,进行单、双、群颗粒的沉降行为模拟,并与前人数值计算结果展开对比。为凸显高解析度CFD- DEM- IBM方法的优势,非解析CFD- DEM方法的计算结果也在文中给出。其中,非解析方法中流固相互作用力依据式(13)计算:

(13)

式中:Cd为阻力系数；ρf为流体密度；di为颗粒pi的直径；uf,i为颗粒pi周围网格点插值得到的流体速度；vi为颗粒pi的速度；εi为pi处的流体体积分数；χ=3.7-0.65exp[-(1.5-lgRei)2/2],为与颗粒雷诺数Rei有关的参数。

非解析方法要求流体网格的尺寸远大于颗粒尺寸[18],考虑到本文算例的具体参数,采用非解析方法计算时,网格尺寸取为约2.5倍颗粒直径。

2.1 单颗粒沉降

为验证本文提出的高解析度CFD- DEM- IBM耦合模型用于分析颗粒沉降问题的正确性与可靠性,首先选择经典的单颗粒沉降问题[19- 20]展开计算。计算域为2 cm×6 cm的矩形域,域内充满密度为ρf=1 g/cm3、黏度为μf=0.1 g/(cm·s)的牛顿流体。初始时刻颗粒位于计算域中线位置,从距离底面4 cm处由静止受重力下落,颗粒直径dp=0.25 cm,密度ρp=1.25 g/cm3,其法向及切向刚度均取为2×107N/m。整个计算域采用规则的矩形网格离散,网格尺寸为1/256 cm,颗粒边界上布置402个浸入边界点,重力加速度g=9.81 m/s2,除上部边界设置为开边界外,其余三边均设置为无滑固壁边界。

表1 最大雷诺数对比

图3对比了单颗粒沉降的垂向位置与垂向速度。由图3(b)可见,颗粒沉降过程的加速沉降、匀速沉降、触底减速沉降3个阶段都得到了很好的再现。值得注意的是,采用传统非解析的CFD- DEM方法的计算结果也呈现在图中,可以看出非解析方法的结果虽与其他方法的结果具有一定差异,但颗粒沉降过程中3个阶段的典型流态、颗粒的稳定沉降速度等均呈现出较好的一致性。

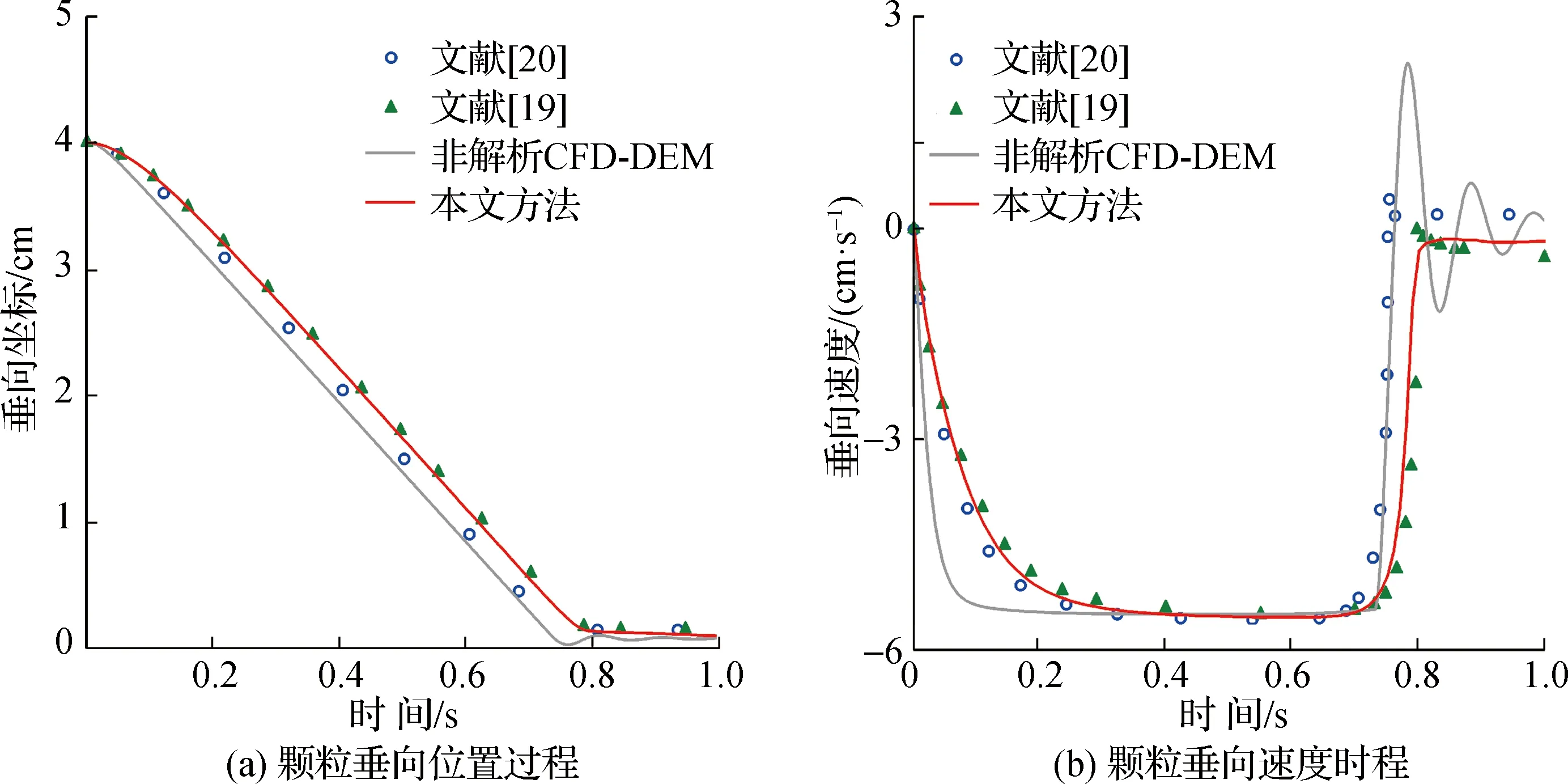
图3 单颗粒沉降垂向位置与垂向速度时程

实际上,非解析CFD- DEM方法要求流体网格的尺寸需远大于颗粒尺寸[18],更适合于规模更大的颗粒沉降问题。而在此算例中,由于颗粒尺寸一定而计算域有限,流体网格尺寸难以达到理想要求,势必造成计算结果与前人研究的差异。总的来说,本文方法与以往研究结果吻合度较高,证明了本文提出的CFD- DEM- IBM方法处理颗粒沉降问题的准确性与可靠性；另外,对于稀疏的颗粒两相流系统,无论是非解析还是解析的CFD- DEM方法均可适用,能够描述颗粒的沉降行为。

2.2 双颗粒沉降的DKT现象

为初步验证本文提出的方法对于稠密颗粒两相流问题的适用性、高解析度描述流场与颗粒行为的能力,进行2个相同圆形颗粒自由下落问题研究。计算域与颗粒大小及网格尺寸等参数与2.1节中取相同,不同之处为本节中流体黏度μf取为0.01 g/(cm·s),颗粒密度ρp取为1.5 g/cm3。如图4(a),初始时刻,两颗粒分别位于((1+0.001) cm,5 cm)及((1-0.001) cm,4.5 cm)处,由静止受到重力作用开始下落。

图4 双颗粒沉降流速矢量

在两同轴颗粒的沉降过程中,初始位于上方的拖尾颗粒将会超越下方引导的颗粒,发生经典的追赶—接触—翻滚(Drafting- Kissing- Tumbling,DKT)现象[21]。如图4所示,下方颗粒沉降过程中产生的低压尾涡结构作用于上方的颗粒,造成上方颗粒受到的阻力降低从而加速下落(图4(b)),直至与下方颗粒接触(图4(c))，最终两颗粒由于接触结构的不稳定而分开(图4(d))。可见,本文方法能够将流场高度解析,正确再现了DKT现象,与文献[21]中的结果具有很好的一致性。

为定量对比计算结果,图5将双颗粒沉降垂向位置与水平位置时程图与前人研究结果展开对比。图中,p1为初始时刻位于上方的颗粒,p2为初始位于下方的颗粒。由图可见,在0.2 s前,采用本文所提出的CFD- DEM- IBM方法进行计算得到的水平与垂向位置与前人[21]的结果都保持高度一致。考虑到翻滚现象主要取决于扰动的发展,受到不同方法实施过程中数值误差的影响,极具不稳定性,在翻滚阶段产生的现象可能会有所不同,这一流场特性将影响颗粒的位置,因此,图5中0.2 s后的结果差异的产生是合理的。

图5 双颗粒沉降垂向位置与水平位置时程

另外,由图5可见,将非解析方法的计算结果与本文方法的计算结果对比发现,非解析CFD- DEM方法计算所得结果完全属于两颗粒单独沉降现象的累加,未能反映出两颗粒间的相互作用,不能考虑到颗粒尾流的影响。对于此类颗粒间存在相互干扰的问题,通过经验公式计算流固耦合作用力做法是不准确的,因此,非解析的CFD- DEM方法不适用于稠密颗粒两相流问题的研究。

2.3 颗粒群沉降

为进一步验证本文所提出的CFD- DEM- IBM方法处理稠密颗粒两相流问题的能力,本节展开了504个圆形颗粒在密闭容器内的沉降过程[22]的数值模拟。封闭的矩形域大小为2 cm×2 cm,其内部流体的密度为ρf=1 g/cm3,黏度为μf=0.01 g/(cm·s)。504个颗粒具有相同的直径dp=0.062 5 cm,密度为ρp=1.01 g/cm3,计算域内颗粒的体积分数为38.66%,初始时刻504个颗粒的位置分布如图6(a)所示。计算域采用1/256 cm的网格进行划分,每个颗粒表面布置150个浸入边界点,计算域的4个边界均设置为无滑固壁。

图6 504个颗粒沉降速度矢量

图6给出了504个颗粒沉降过程中的速度矢量图。可见,沉降开始时,在重力作用的影响下所有颗粒都均匀下落；由于壁面的阻滞效应,靠近两侧壁面逐渐形成一对涡结构,且在t=1 s到t=3 s间可以观测到Rayleigh- Taylor不稳定性的发展；随后,在t=3 s到t=5 s间,颗粒被涡结构带向计算域底部,计算域下方持续能够观察到涡结构的变化；继而,一部分粒子被带往计算域上方,但最终,计算域内的涡结构趋于消散,整个稠密颗粒两相流系统近乎稳定下来。

通过定性分析可知,504个颗粒的沉降行为与文献[22]中的结果具有较高的一致性。通过壁面阻滞效应及涡结构的形成与演化的成功模拟、稠密颗粒系统主要运动特征的正确捕捉,反映出本文所提出的CFD- DEM- IBM方法处理颗粒间碰撞、计算流固两相间耦合作用力、处理颗粒与壁面碰撞行为的准确性与可靠性。总的来说,对该问题的精确再现也进一步证明了本文所提出的方法处理稠密颗粒两相流问题的能力以及对流场的高精度解析。