溢流堰与竖缝组合式鱼道紊流结构试验研究
2021-04-12董志勇余俊鹏
董志勇,余俊鹏,黄 洲
(浙江工业大学土木工程学院,浙江 杭州 310023)
随着经济社会的快速发展,人们对水资源的需求日益增长,在河流上修筑了许多水闸、大坝等水工建筑物,这些工程在兴利除害的同时对生态环境也带来一些影响[1],例如对鱼类洄游造成阻碍。鱼道作为一种生态补偿工程,对于保护鱼类资源,恢复河流生物多样性起着重要作用[2]。已有研究资料[3]表明,在全球已建成的鱼道中,鱼类能够溯游通过的鱼道尚不足一半。因此,研究鱼道水力特性,尤其是鱼道紊流结构的特征,对鱼道设计具有重要的指导意义。
鱼道型式可大致分为竖缝式、堰流式、孔口式及其组合式等几种型式。竖缝式鱼道对水位变化的适应性较好,Guiny等[4]对竖缝式鱼道的水力特性和生物特性进行过较为系统的试验研究;孙双科等[5]对北京市上庄新闸竖缝式鱼道的水力特性做过模型试验研究;董志勇等在大比尺鱼道模型中试验研究了同侧竖缝式鱼道的水力特性[6],此外,还试验研究了异侧竖缝式鱼道的水力特性[7]。堰流式鱼道适宜于具有跳跃性的鱼类,Rajaratnam等[8]提出了预测堰流式鱼道水流流态从跌落流到滑移流的判别标准;Kim[9]试验研究了不同堰型的水力特性及其对溢流堰鱼道中鱼类溯游的影响。关于紊流结构对鱼类溯游行为影响的研究,Enders等[10]研究了紊动对大西洋鲑鱼游泳能量消耗的影响;Liao等[11]阐述了鲑鱼在旋涡之间改变游泳姿态可以减少其轴向肌肉活动,表明合适的紊流结构有助于鱼类溯游;Liu等[12]研究了不同坡度竖缝式鱼道水流的平均动能、紊动能、紊动强度及雷诺应力;Lacey等[13]基于紊流的强度、周期、方向、规模4个特征,研究了鱼类在紊流中的游泳行为。迄今为止,人们对单一式(竖缝式、堰流式、孔口式)鱼道研究较多,对于组合式鱼道则仅有些数值模拟研究[14- 16],而对于组合式鱼道紊流结构的试验研究,迄今鲜有文献报导。由于沿海、沿江洄游性鱼类众多,其溯游习性各异,传统的单一式鱼道难以满足不同鱼类的溯游习性。
本文在大比尺鱼道水槽中试验研究了凹口溢流堰与竖缝同侧布置组合式鱼道的紊流结构,以期提高人们对此种组合式鱼道紊流结构的认识,为优化鱼道设计、修复鱼类生境提供参考。
1 试验设备与量测技术
试验在浙江工业大学水力学实验室大比尺鱼道水槽中进行。鱼道水槽长20.0 m,宽0.6 m,深1.0 m,水槽主要由3段组成,即入流段、工作段及出流段。工作段由4个水池组成,其两侧为有机玻璃,水池沿流动方向呈阶梯式,阶梯高度为5 cm。凹口堰与竖缝组合式隔板在阶梯以上高度均为65 cm,凹口堰宽20 cm,深25 cm,竖缝宽10 cm。三维流速由SonTek公司的Micro ADV量测,流量由出流段的矩形堰测读。

图1 鱼道水槽坐标系示意
鱼道水槽坐标系定义如图1所示,坐标原点位于水池上游组合式隔板右下角,沿水槽纵向设为x轴,横向为y轴,垂向为z轴。竖缝采取同侧布置方式,沿垂向(z向)取不同深度水平面(10 cm、20 cm、30 cm、40 cm、44 cm、48 cm),每一水平面沿纵向(x向)取多条横线(5 cm、10 cm、15 cm、20 cm、30 cm、50 cm、70 cm、90 cm、110 cm、130 cm、150 cm、160 cm、165 cm、170 cm、175 cm),在每条横线(y向)上布设多个测点(5 cm、7.5 cm、10 cm、15 cm、20 cm、24 cm、28 cm、32 cm、36 cm、40 cm、45 cm、50 cm、52.5 cm、55 cm、57.5 cm)。试验流量Q=49.7 L/s,相应的水池断面平均流速U=15.9 cm/s。以3号水池作为试验水池,水池长L=180 cm,水池宽B=60 cm,池内水深H=52 cm。定义z=0~20 cm为水池底层,z=20~40 cm为水池中层,z=40~52 cm为水池表层。工作段水池水位采用自动水位测量系统实时量测。
2 试验结果与讨论
2.1 三维时均流速
2.1.1 纵向流速
水池前部纵向流速沿横向分布如图2(a)所示,从图中可以看出,表层z=48 cm由于受到凹口堰跌落射流的影响,凹口堰附近纵向流速较大,其他深度的纵向流速沿横向分布具有壁面射流流速分布的特征。平面壁面射流分布规律如图中实线所示,可表示为
(1)
式中:u为纵向流速,cm/s。

图2 不同横断面上纵向流速沿横向分布
图2(b)为水池后部纵向流速沿横向分布,由图可见,相对于水池前部,凹口堰对表层水流的影响明显小于水池前部,图中实线为壁面射流,可表示为
(2)
2.1.2 横向流速与垂向流速
图3为水池横向流速沿横向分布,除表层外,其他深度的试验点可拟合为
(3)
式中:v为横向流速,cm/s。
从图中可以看出,除堰流区表层外,水池后部横向流速基本为负值,表明水流受隔板阻挡形成冲击射流,往远离竖缝的方向流动,从而形成回流。水池垂向流速沿横向分布如图4所示,垂向流速可拟合为
(4)
式中:w为垂向流速,cm/s。

图3 横向流速沿横向分布(x=175 cm)

图4 垂向流速沿横向分布(x=90 cm)
2.1.3 最大纵向流速衰减规律
三维紊动射流按其最大速度衰减率可分为3个明显不同流动区域,即势流核心区、特征衰减区和径向型衰减区,可表示成幂函数形式:
(5)
式中:um为任意x处的最大流速,cm/s;R为出流孔水力半径,cm;n为衰减指数。

图5 最大流速沿程衰减
不同深度最大流速沿程衰减如图5所示,依照式(5),x/R在0~10内可拟合为一条直线,x/R>10可拟合为
(6)
与平面自由壁面射流对比,组合式鱼道的壁面射流区存在势流核心区和特征衰减区,但未出现径向型衰减区,且特征衰减区的表层流速衰减相对缓慢,主要是由壁面射流卷吸所致。
2.2 紊动强度
紊动强度是表征流速脉动强弱的一个特征量,可表示为
(7)
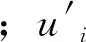
图6(a)为纵向紊动强度沿横向分布,由图可见,纵向紊动强度在堰流区较大,其他区域则较平缓。由于凹口堰跌落射流流速较大,卷吸周围流体和剧烈掺混,致使堰流区表层的紊动强度较大。横向紊动强度沿横向分布如图6(b)所示,从图中可以看出,水池中部横向紊动强度为中间大两边小,呈上凸型分布。

图6 紊动强度变化
2.3 雷诺应力
雷诺应力的变化取决于紊流的扩散、产生、耗散及应力应变的综合效应。相对雷诺应力可表示为
(8)
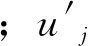
水平面(z=48 cm)上雷诺应力(ηxy)沿横向分布与纵剖面(y=32 cm)上雷诺应力(ηxz)沿程变化如图7所示,由图可见,水池前部堰流区和竖缝壁面射流区表层的雷诺应力较大,且堰流区左右两侧雷诺应力方向相反,中部和后部的雷诺应力相对较小。堰流区表层前部的雷诺应力明显比中、后部大,中、底层则基本沿程不变,表明凹口堰跌落射流对表层雷诺应力影响较大,主要是由跌落射流剧烈紊动掺混所致。

图7 雷诺应力变化
2.4 自相关系数
流场中某一特征点不同时段τ的相关系数,称为该点的自相关系数RL,可表示为
(9)
式中:u′(t)为特征点t时刻的纵向脉动流速;u′(t+τ)为特征点t+τ时刻的纵向脉动流速。
水池中部水流特性对鱼类的溯游有着重要影响,因此,分析水池中部表层不同区域的自相关系数变化具有重要意义。水池中部表层不同区域自相关系数如图8所示。从图中可以看出,竖缝壁面射流区的自相关系数相对于堰流区略小,但周期更短,表明竖缝壁面射流区的涡旋变化较快,涡旋之间的相关性比堰流区差。

图8 自相关系数
2.5 紊动尺度
对自相关系数进行时间积分可以得到相应的积分时间尺度ΛL,以衡量紊流场中不同涡旋的平均尺度,可表示为

(10)
图9为不同区域积分尺度变化情况,从图中可以看出,堰流区的积分尺度远大于竖缝壁面射流区,且随时间呈不断增大的趋势,表明在堰流区存在较大尺度的涡旋结构。
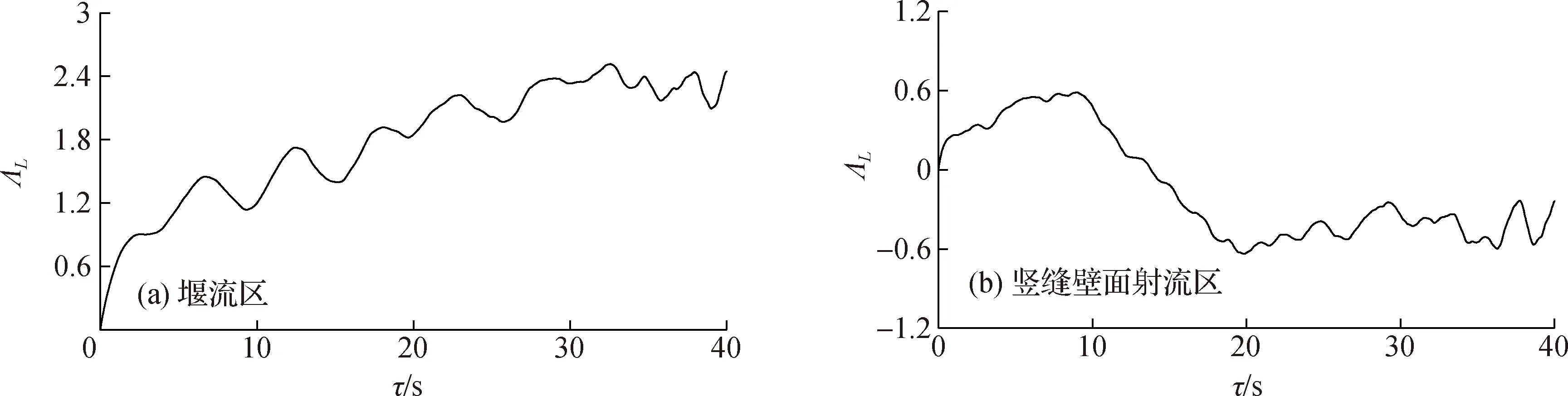
图9 积分尺度
将自相关系数对时间求二次导数可以得到相应的微分时间尺度λL,表征引起脉动流速当地变化的微小涡旋平均大小的一种度量,可表示为
(11)
图10为不同区域微分尺度变化情况,从图中可以看出,竖缝壁面射流区的微分尺度明显比堰流区微分尺度大,意味着竖缝壁面射流区的微小涡旋比堰流区多。竖缝壁面射流区大部分都是一些微小的涡旋,而堰流区的涡旋尺度则明显比竖缝壁面射流区大。

图10 微分尺度
3 结 论
通过声学多普勒测速仪实测溢流堰与竖缝组合式鱼道的三维瞬时流速,得到以下主要结论:
(1) 鱼道水池内有两股水流相互作用影响,纵向流速起主导作用。
(2) 堰流区的跌落射流对紊动强度和雷诺应力都有较大的影响,紊动强度和雷诺应力均在此处出现峰值,这种紊流结构有助于吸引具有跳跃习性的鱼类过堰。
(3) 堰流区易于产生大尺度涡旋,竖缝壁面射流区则生成许多小尺度涡旋。
(4) 相比于单一式鱼道,溢流堰与竖缝组合式鱼道水流流态受凹口堰跌落射流和竖缝壁面射流共同作用,呈现出复杂的三维紊流结构。
