单指标模型自适应局部惩罚样条估计
2021-04-12赵静
赵 静
(天津财经大学 统计学院,天津 300202)
一、引 言
回归分析在统计学中具有十分重要的地位,是应用最广泛的分析方法之一。回归分析大致分为参数模型及非参数模型。参数模型通常假定函数基本形式已知、参数未知,通过对参数的估计得到函数关系的表达式,从而进行分析、预测等。参数模型的优势在于理论完善,形式简洁,实际应用广泛,但由于拟合能力不足,存在模型设定错误等,因而学术界提出了非参数模型。非参数模型的主要特点在于回归函数的形式任意,对协变量和响应变量的分布限制较少,具有较大的适应性与稳健性。与传统回归模型相比,非参数模型具有更多的灵活性,可以对同一数据进行多次拟合,深入探究数据中可能存在的某种隐藏关系。而且,非参数模型可以对数据中的任何模式或变量间任何一种曲线关系进行拟合,而传统回归只能对直线或二次曲线等形式进行拟合。实际上,非参数回归拟合往往也会带来意想不到的结果,会改变人们对数据进行进一步分析的方向,得到更深刻的结论。在非参数模型中通常假定函数形式未知,需要由观测数据本身对整体函数进行估计,进而得到拟合效果更好的模型[1]。
单指标模型是一种应用背景广泛的非参数模型,它的优势在于能够有效地避免“维度灾祸”问题,很多学者对此进行了研究。Ichimura采用了回归模型中最小二乘估计,并结合N-W估计法对模型指标参数进行了估计[2];Weisberg等基于以上方法证明了指标参数估计量的相合性[3];Xia等提出了最小平均方差估计法,构造的指标函数在联系函数欠光滑的情况下估计结果也具有良好的收敛性,同时Xia证明了最小平均方差估计的渐近性[4-5];Jiang等提出了纵向和函数响应数据的单指标模型,并采用指标函数的初始估计,证明了估计量的相合性和渐近性[6]。
为避免模型中出现过拟合的情况,Eilers等以B样条为基函数,在目标函数中加入基函数系数的二阶差分作为惩罚[7];Ruppert等以截断幂基函数为基础,取系数的平方和作为惩罚项,得到函数系数的惩罚样条估计值[8];Yu等提出了截断幂基函数的部分线性单指标模型的惩罚样条估计,通过“去一分量”法及最优化算法得到参数的估计值,并证明了估计量的相合性和渐近性[9]。
由于惩罚样条模型中对基函数的惩罚权重是相同的,因此将上述惩罚方法称为均匀惩罚样条或整体惩罚样条估计法。Ruppert等提出了一种基于网格搜索及线性插值技术的局部惩罚样条估计方法,该方法充分考虑数据异质性,但计算较为复杂[10];丁梦珍等针对非参数模型,提出了基于极差调节的局部惩罚样条估计方法,将各节点区间数据的极差值作为反映该区间数据波动性的依据,构造递减函数,生成局部惩罚权重,并得到函数系数估计值,但由于对节点区间内存在数据异常值的情况没有充分考虑,若某区间具有数据异常值时,此方法会错误地判断该区间数据的波动性[11];江坤等针对非参数模型,提出了一种基于方差的局部样条估计方法,虽然各区间数据量纲相同,但由于均值不同,直接使用方差作为数据离散程度的判断是不充分的[12]。
针对单指数模型,本文以径向基函数作为样条函数,提出了一种基于变异系数的局部惩罚样条估计方法。通过变异系数反映各区间数据的离散程度,并构造递减函数生成局部惩罚权重向量,得到局部惩罚样条函数系数的估计值,再结合“去一分量”法和Levenberg-Marquardt算法迭代得到单指标模型指标参数的估计值,采用Monte-Carlo模拟验证了该方法的正确性和有效性。
二、基于径向基均匀惩罚样条估计
假设非参数模型为:
yi=g(xi)+εi
(1)
其中i=1,2,…,n,εi~N(0,σ2)。
Ruppert描述了径向基的惩罚样条估计,进一步考虑p次样条径向基函数为:
x=(1,x,x2,…,xp-1,|x-k1|2p-1,…,|x-kl|2p-1)
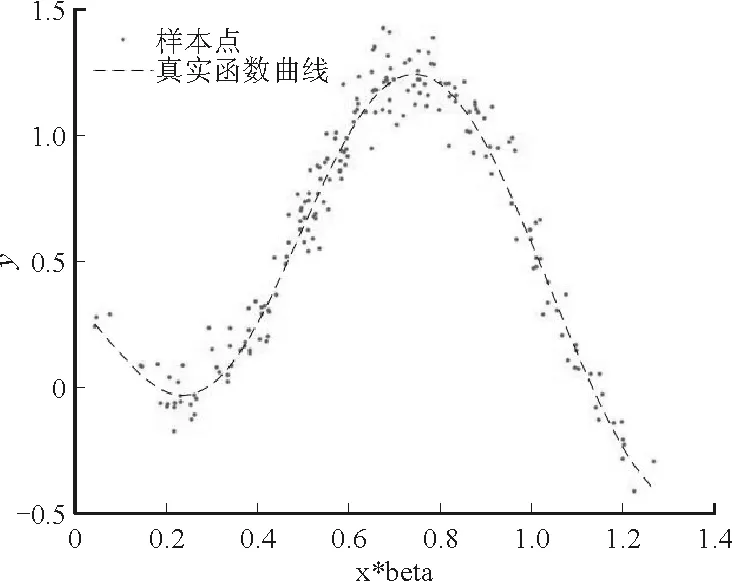
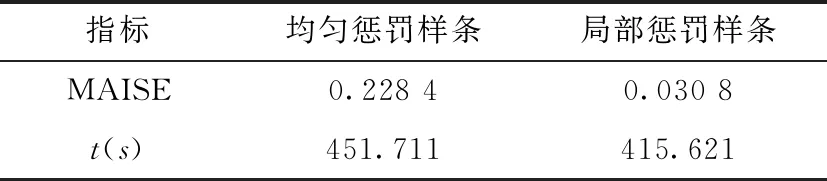
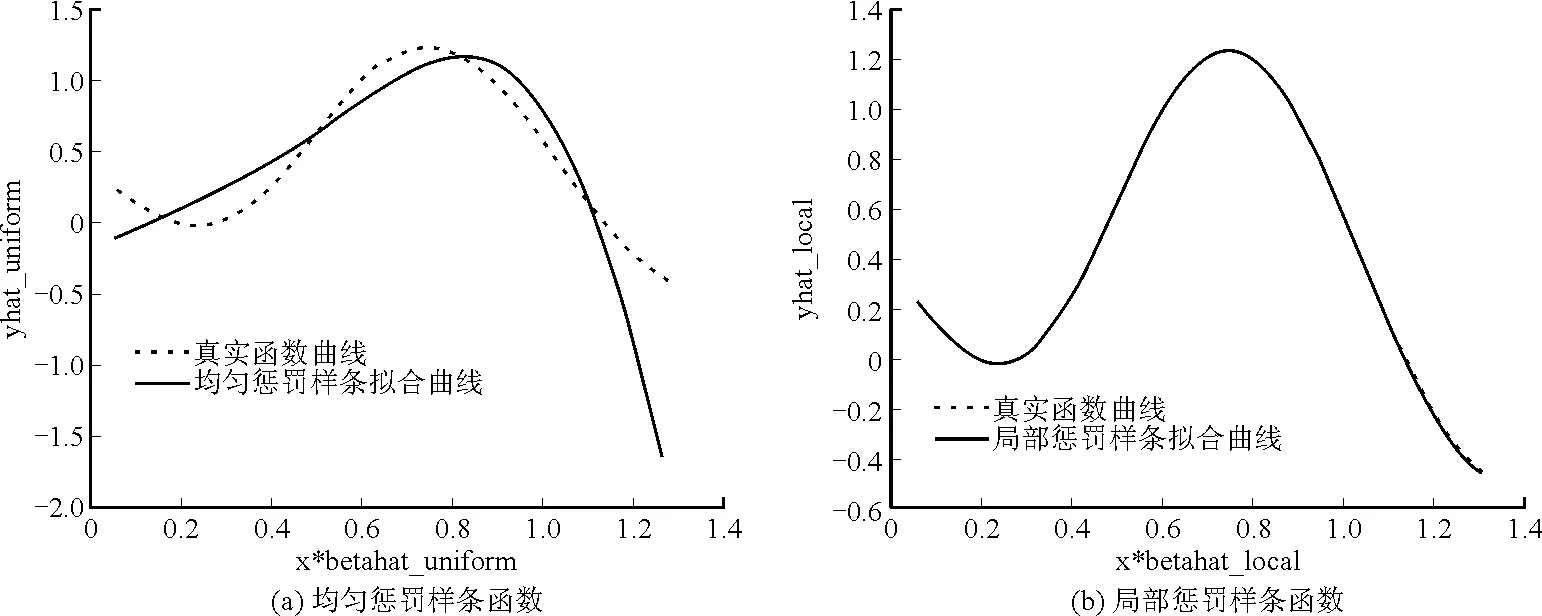
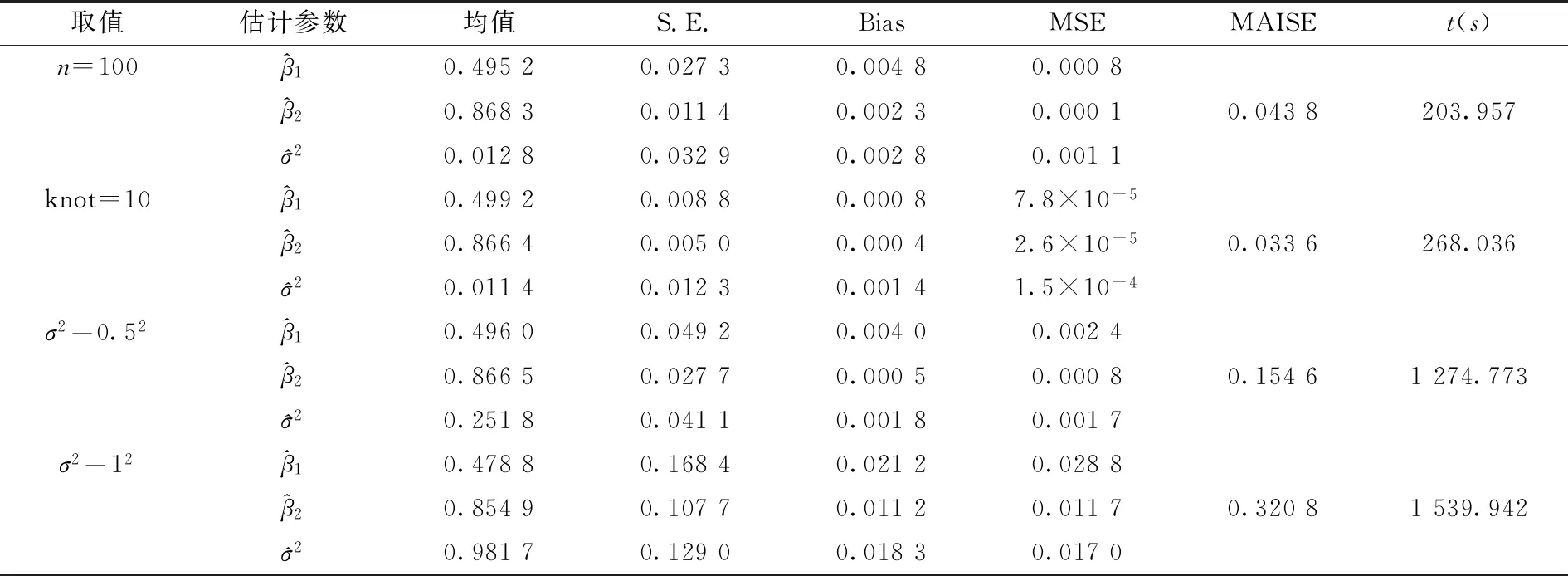
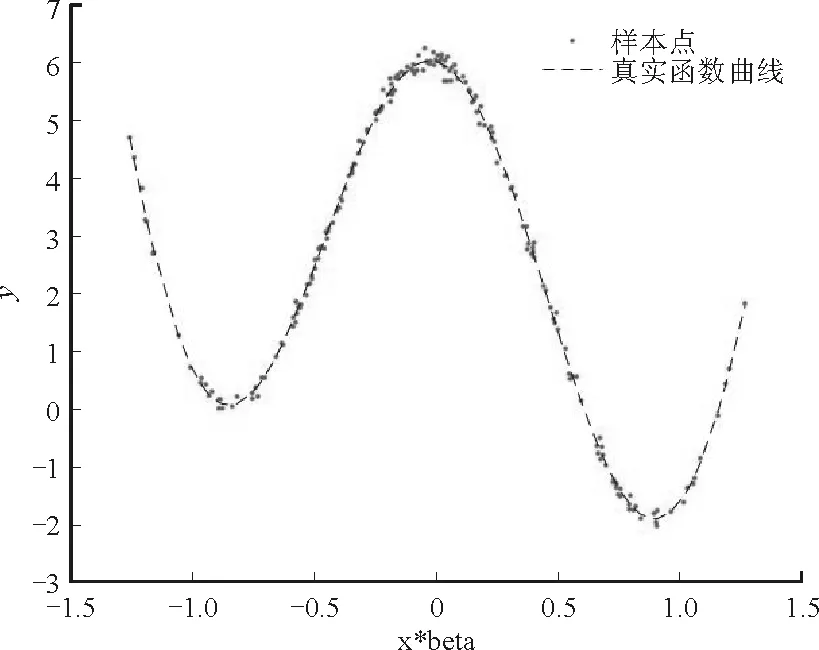
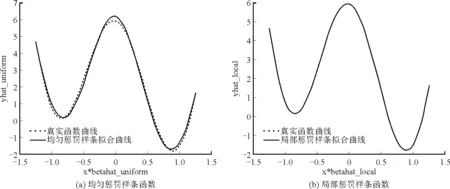
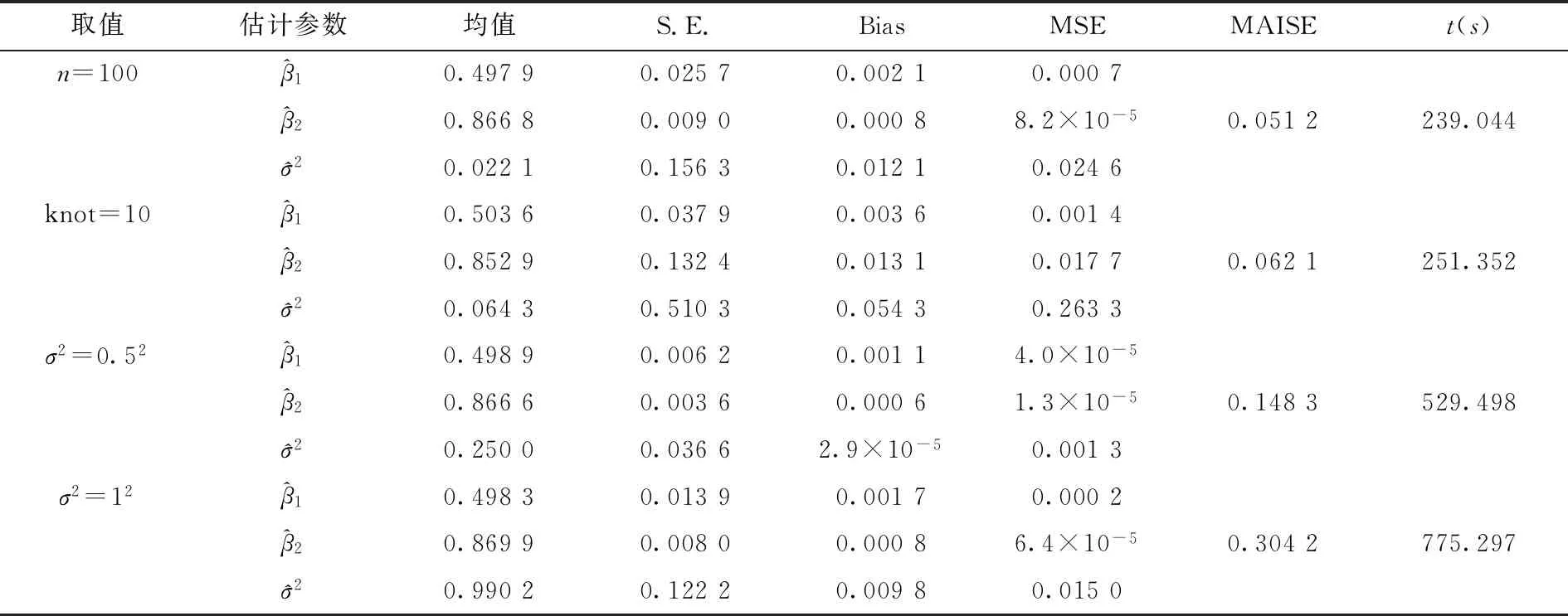
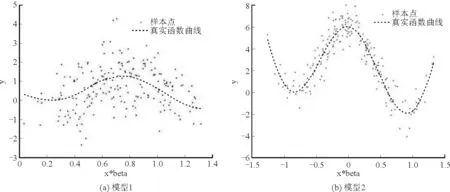
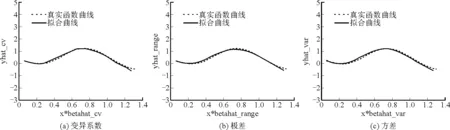
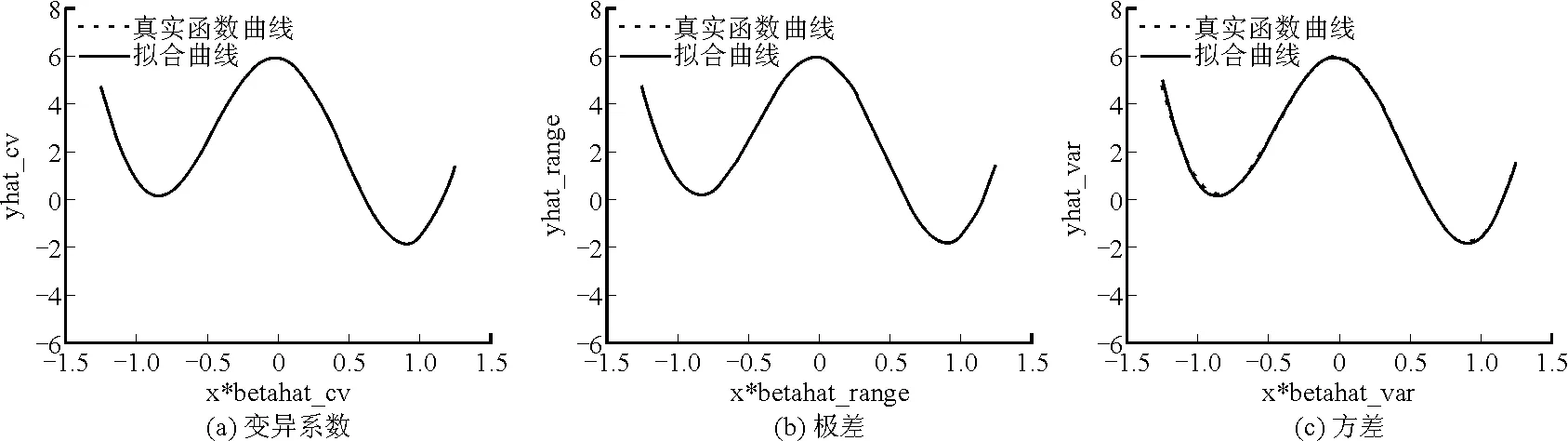
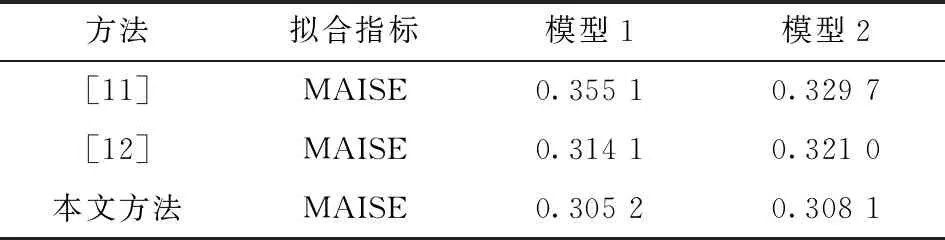
其中a≤k1<… (2) 令Y=(y1,y2,…,yn)T,X=(x1,x2,…,xn)T,则式(1)的目标函数可以表示为: Q(α)=‖Y-Xα‖2+λαTDα (3) 其中λ为惩罚参数,D为径向基惩罚矩阵,通常设定为: (4) 其中 当节点固定时,函数系数的总惩罚量只依赖惩罚参数λ,因此将此类方法称为均匀惩罚样条回归或整体惩罚样条回归。 设单指标模型形式为: (5) 其中xi=(xi1,xi2,…,xid)T为观测变量,β=(β1,β2,…,βd)T为未知指标参数,yi为解释变量,εi独立同分布,服从均值为0方差为σ2的正态分布。为了模型的可识别性,假定‖β‖=1且β的第一个非零元素为正,通过模型可以看出,当d=1且β=1时,模型转化为非参数模型。 设径向基函数系数为α=(α0,α1,…,αp-1,αp,…,αp+l-1)T,则g(ui)≈δ(ui)α,(i=1,2,…,n),将其代入单指标模型(5),为了估计径向基函数系数和指标参数β,最小化式(6): (6) 其中λ为惩罚参数且λ>0,D为惩罚矩阵,惩罚矩阵的设置如式(4)所示。此时,通过最小化Qn,λ把计算未知系数函数与指标参数的问题转化为估计向量α和β的问题。 用矩阵形式表示,令Y=(y1,y2,…,yn)T,X=(x1,x2,…,xn)T,δ(U)=(δ(u1),δ(u2),…,δ(un))T,ε=(ε1,ε2,…,εn)T,则式(5)可以表示为: Y=g(Xβ)+ε 局部惩罚样条估计从直观上来说,当观测数据在节点具有较大的波动性时,应当给予其较小的惩罚,使得拟合曲线在该区间处具有较大的自由,反之,若观测数据在节点中波动性较小时,应当给予较大的惩罚,限制拟合曲线在该区间的自由。基于此想法,我们使用变异系数作为波动性判断依据,通过构造递减函数,得到局部惩罚权重设置。 设局部惩罚权重向量ω=(0,0,…,0,ω(k1),…,ω(kl)),其中ω(ki)表示对第i个节点处的系数的惩罚,取对角矩阵: R=diag(0,0,…,0,ω(k1),…,ω(kl)) 将R代入式(6),则: 其中Q=RTDR。 对于权重ω(k1),ω(k2),…,ω(kl)的设置,采用节点间观测数据的变异系数来反映局部波动性,即: ω(km)=-ln|cvm|,m=1,2,…,l 基于以上思想,给出单指标模型局部惩罚样条估计步骤,具体如下: 则: (7) 则拟合值为: 对于第一步给定的初始值β0,采用Yu等提出的方法,选定线性模型: 通过极小化线性模型得到β的初值β0: 局部惩罚参数λ通常使用广义交叉验证法(Generalized-cross-validation,GCV)准则计算: 本章通过Monte-Carlo模拟探究局部惩罚样条估计在有限样本下的表现。分别采用估计标准误(S.E.)、偏差(Bias)、均方误(MSE)以及真实函数与拟合值的平均偏差平方根(MAISE)作为评估指标。 本文选取两个模型进行模拟,并且分别比较了不同样本量n、不同误差项方差σ2以及选择不同节点步长knot情况下参数的估计及评估指标结果,具体模型设定与结果如下。 模型1: 图1 模型1数据及真实函数图 表2中MAISE反映了样条函数的拟合情况,可以看出,均匀惩罚样条估计下的MAISE为0.228 4,局部惩罚样条估计下的MAISE为0.030 8,局部惩罚样条的MAISE小于均匀惩罚样条,说明局部惩罚样条估计下的样条函数拟合效果优于均匀惩罚样条。 表2 模型1拟合指标及时间消耗 模拟200次拟合图像如图2所示,其中(a)为均匀惩罚样条函数拟合图,(b)为局部惩罚样条函数拟合图。 图2 模型1样条函数拟合图 从图2明显可以看出,局部惩罚样条函数拟合优于均匀惩罚样条函数,局部惩罚样条函数拟合的曲线更接近真实函数曲线。 分别选取样本量为n=100,节点步长knot=10,误差项εi~N(0,0.52)和εi~N(0,12),局部惩罚样条估计结果如表3所示。 对比表1、表2和表3可以看出,当样本量选取n=100时,参数估计均值接近真实值,但偏差、均方误均大于样本量n=200的偏差值与均方误差值。从拟合效果来看,n=100时MAISE为0.043 8,大于0.030 8,说明随着样本量的增大,参数估计的精确性越好,越接近真实值,函数拟合效果越好。比较运行时间可以看出,随着样本量的增加,在得到较精确的估计值时,估计所花费的时间也随之增加。当节点步长选取knot=10时,参数估计值及函数拟合值MAISE大于knot=5的数值,所花费的时间268.036小于415.621,说明节点步长选取越小,节点越密集,参数估计的精确性越好,拟合效果越好,但是计算时间会增加。同理,当误差项方差分别选取σ2=0.52与σ2=12时,参数估计效果及函数拟合值MAISE均明显不如σ2=0.12的估计结果,同时对比σ2=0.52与σ2=12来看,随着误差项方差的减小,参数估计的精确性越好,函数拟合效果越好,花费的时间越少。 表3 模型1不同样本量、误差项方差及节点步长参数估计结果 模型2: 其中误差项εi~N(0,0.12),样本个数n=200,xij独立随机从均匀分布U(-1,1)上取值,选择节点步长knot=5,真实函数g3(t)=exp{-t},g4(t)=3t2,g5(t)=5cos(tπ)。选取一组模型数据散点图及真实函数曲线如图3所示。 图3 模型2数据及真实函数图 模型200次估计及评估结果见表4,拟合结果与运行时间见表5。 由表4和表5对比均匀惩罚样条与局部惩罚样条参数估计结果可以看出,在200次模拟的情况下,局部惩罚样条估计的参数及函数拟合效果均优于均匀惩罚样条。 表4 模型2参数估计结果 表5 模型2拟合指标及时间消耗 模拟200次拟合图像如图4所示,其中(a)为均匀惩罚样条函数拟合图,(b)为局部惩罚样条函数拟合图。 由图4可以看出,虽然均匀惩罚样条与局部惩罚样条函数拟合都接近于真实函数,但是局部惩罚样条函数拟合图像与真实函数图像几乎重合,表明局部惩罚样条函数拟合效果优于均匀惩罚样条函数。 图4 模型2样条函数拟合图 另外类似于模型1,分别选取样本量为n=100,节点步长knot=10,误差项εi~N(0,0.52)和εi~N(0,12),局部惩罚样条估计结果如表6所示。由表6可以得到相同的结论,即随着样本量的增加,参数的估计值越精确,函数的拟合效果越好,但所花费时间略有提高;随着节点步长的减小,节点个数增多,参数的估计值越好,函数的拟合效果越好,但花费时间有所提高;随着误差项方差的减小,样本点在真实函数周围波动性越小,参数的估计和函数的拟合效果越好,同时花费时间越少。 表6 模型2不同样本量、误差项方差及节点步长参数估计结果 接下来,使用模型1与模型2,分别将于梦玲等与江坤等提出的方法与本文提出的方法做对比实验[11-12]。算法方面:将他们的方法分别嵌入单指标模型中,其它算法均与本文相同,局部惩罚力度均设定为5。模型方面:对于模型1,xij从均匀分布U(0,1)上随机取值,对于模型2,xij从均匀分布U(-1,1)上随机取值。其它参数均设置为:样本量n=200,节点步长knot=5,误差项方差σ2=1,样条函数阶数p=3,模拟次数mcn=200。选取一组真实数据及函数曲线如图5所示。 图5 模型数据散点及真实函数曲线图 图6 模型1拟合图 图7 模型2拟合图 拟合评价指标MAISE如表7所示。可以看出,本文使用的方法在模型1中的MAISE为0.305 2,在模型2中的MAISE为0.308 1,均小于其它两种方法,说明本文方法在拟合上效果略好。 表7 不同方法拟合指标比较结果 针对单指标模型,本文提出了一种基于变异系数调节的局部惩罚样条估计方法,相比较常使用的均匀惩罚样条估计方法,基于变异系数的局部惩罚样条估计方法充分考虑数据纵向上的信息,克服了均匀惩罚样条估计方法因各节点惩罚权重的一致,导致模型对于复杂数据的拟合缺乏自适应性的缺点。 在基于变异系数的局部惩罚样条估计方法中,以各节点相邻区间内数据的变异系数数值的大小来衡量数据的离散程度,通过计算所得的各节点的变异系数值,构造递减函数生成局部惩罚权重向量,结合径向基函数,给出了局部惩罚样条函数系数估计值。然后,通过“去一分量”法及Levenberg-Marquardt优化算法,迭代得到最优指标参数估计值。本文的估计方法具有较好的自适应性,在数据离散程度大的区间,会给予拟合曲线较小的惩罚,以提高拟合效果;在数据离散程度小的区间,会给予拟合曲线较大的惩罚,以保证曲线的光滑。模拟仿真探究了有限样本下单指标模型局部惩罚样条估计方法的正确性和有效性,从而使拟合曲线能够自适应地反映不同区间的数据特征。 模拟仿真结果表明,基于变异系数的局部惩罚样条估计结果优于均匀惩罚样条估计结果,同时基于变异系数的局部惩罚样条估计的曲线拟合结果也优于均匀惩罚样条。样本量的多少、选择节点步长的大小以及误差项方差的大小都会影响模型的估计效果。对比实验结果表明,随着样本量的增加,节点步长的减小,或者误差项方差的减小,参数的估计值会更精确,函数的拟合效果更好。另外,本文还比较了计算花费时间,带来良好估计结果的同时所需要的计算时间也不同,因此在应用中合适的选取是非常重要的。最后,与基于极差和基于方差的局部惩罚样条估计方法做了对比实验,结果表明基于变异系数的局部惩罚样条估计方法在拟合效果上略优于基于极差和基于方差的局部惩罚样条估计方法。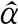
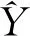
三、单指标模型局部惩罚样条估计
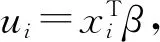
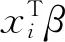


四、模拟仿真
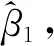


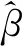
五、结 论
