n值乘积命题逻辑系统的真度研究

南 宁，金明慧，惠小静

(延安大学 数学与计算机科学学院，陕西 延安 716000)

以王国俊教授为首的学者提出了计量逻辑学[1-4]，在多值命题逻辑系统中提出了公式的真度概念，以此为基础大量学者针对不同的逻辑系统对真度展开了相关研究[1-15]。

文献[12]与文献[13]在n值乘积系统的基础上引入了对合否定～和连接词△两类算子，△算子具有去模糊化的特性。这样基本逻辑系统BL在增加了△算子后被扩张为BL△逻辑系统，同时与对合否定连接词结合形成SBL～系统，在该系统中△演绎定理和强完备性定理都是成立的，因此弥补了Gödel和Goguen系统中的不足，使得相关研究得以顺利展开。本文对n值Goguen命题逻辑系统进行公理化扩张记为Goguen～，△。在该系统中添加了新的连接词～，△，给出了Goguenn值命题逻辑系统中命题公式的真度、相似度和伪距离的定义，证明了该真度的MP规则、HS规则及相关性质。

1 预备知识

定义1.1[15]BL△的公理系统如下：

(BL)BL的公理系统；

(A△1)△A∨△A；

(A△2)△(A∨B)→(△A∨△B)；

(A△3)△A→A；

(A△4)△A→△△A；

(A△5)△(A→B)→(△A→△B)。

BL△中的推理规则是MP规则与△规则，其中MP规则是从A，A→B推得B。△规则为A→△A。

定理1.1(演绎定理)[15]令是BL△的公理化扩张，那么对任意理论Γ，公式A和B，有Γ，A├B当且仅当Γ├△A→B。

定理1.2(强完备性定理)[13]设为SLB～系统的公理化扩张，那么理论Γ与公式A，如下条件等价：

(i)Γ├A；

(ii)对每个代数与理论Γ的每个模型e，均有

e(A)=1。

2 命题公式的真度定义及等价形式

定义2.1 设S={p1,p2,…}是可数集，～，△分别是S上的一元运算，∧，∨→分别是S上的二元运算，F(S)是由S生成的(1,1,2,2,2)型自由代数，则称F(S)中的元为命题公式或公式，称S中的元为原子公式。

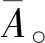
定义2.3 Goguen命题逻辑系统也叫乘积系统，记。

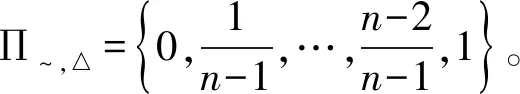
x∨y=max{x,y},x∧y=min{x,y},

称Goguen～，△是n值乘积命题逻辑系统的扩张，简记为～，△。

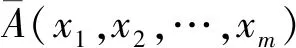
其中|E|表示集合E中元素的个数，称τn(A)为公式A的真度。

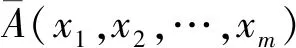
(2)τn(～A)=1-τn(A)。

证明(1)结合定义2.4知，只需证明

设Ei={(x1,x2,…,xm)∈

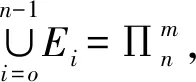
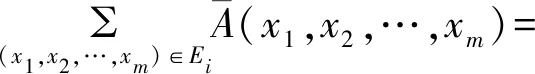
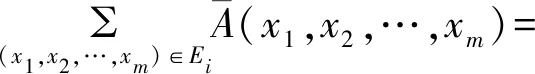
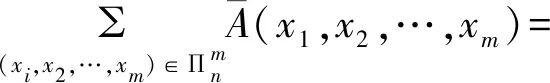
(2)任意的a∈n，～a=1-a，故有

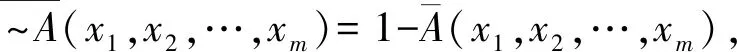
所以由定义2.4知：τn(～A)=1-τn(A)。

命题2.1 设A，B∈F(S)，则

(1)A为重言式当且仅当τn(～A)=0；A为矛盾式当且仅当τn(～A)=1；

(2)A≈B当且仅当τn(A)=τn(B)；

(3)τn(△A→△B)=τn(～△B→～△A)；

证明(1)由定义2.4知，A为重言式当且仅当τn(A)=1。又由定理2.1知，τn(～A)=1-τn(A)=1-1=0，所以A为重言式当且仅当τn(～A)=0。

同理可证，A为矛盾式当且仅当τn(～A)=0。

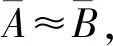
(3)设A,B中含有相同的原子公式p1，p2，…pm,由于对任意的a,b∈n，△a→△b=～△b→～△a，所以对任意的有有

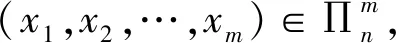
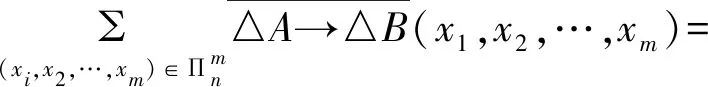
τn(△A→△B)=τn(～△B→～A)。

(4)设A,B中含有相同的原子公式p1,p2，…,pm，由于A→B，因此，对任意的又由于

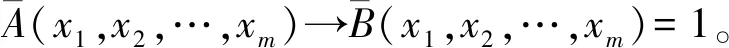
因此对任意的

结合定理2.1知τn(B)≥τn(A)，再结合定理2.1得

τn(～B)≤τn(～A)。

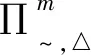
b≥a+(a→b)-1。

证明首先令λ=b-a-(a→b)+1，再分2种情况进行讨论：

(1)当a≤b时，λ=b-a≥0；

(2)当a>b时，

综上，得b≥a+(a→b)-1。

定理2.2 (真度MP规则)设A，B∈F(S)，若τn(△A)≥α，τn(△A→～B)≥β，则

τn(～B)≥α+β-1。

由引理2.1知，

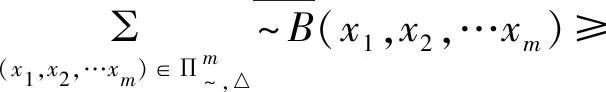
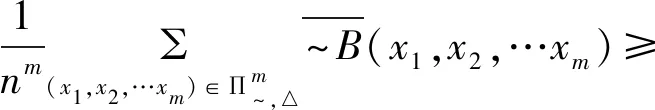
结合定理2.1得τn(～B)≥α+β-1。

定理2.3 (真度HS规则)设A，B，C∈F(S)，若τn(△A→～B)≥α，τn(～B→～C)≥β，则

τn(△A→～C)≥α+β-1。

证明设A，B，C含有相同的原子公式p1,p2，…,pm，易知∀a,b,c∈～,△，

有(△a→～b)→((～b→～c)→(△a→～c))=1，

所以(△A→～B)→((～B→～C)→(△A→～C))是重言式。对∀(x1,x2,…,xm)∈～,△，有

τn((～B→～C)→(△A→～C))≥

τn(△A→～B)≥α，

则τn(△A→～C)≥τn(～B→～C)+

τn((～B→～C)→(△A→～C))-1≥α+β-1，

故证得τn(△A→～C)≥α+β-1。

3 命题公式间中的相似度和伪距离

定义3.1 设A，B∈F(S)，则

ξn(A,B)=τn((A→B)∧(B→A))，称ξn(A,B)为公式A与B之间的相似度。

定理3.1 设A,B∈F(S)，则

(1)ξn(△A，～B)=ξn(～B,△A)；

(2)ξn(△A∨～B,△A)=τn(～B→△A)。

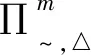
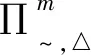
(△a→～b)∧(～b→△a)=

(～b→△a)∧(△a→～b)，所以

(△A→～B)∧(～B→△A)=

(～B→△A)∧(△A→～B)，从而

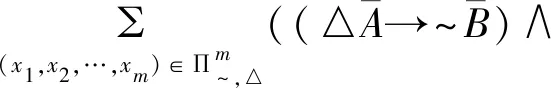
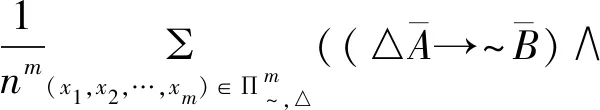
由定义2.4得，

τn((△A→～B)∧(～B→△A))=

τn((～B→△A)∧(△A→～B))，

因此

ξn(△A,～B)=ξn(～B,△A)。

(2)ξn(△A∨～B,△A)=

τn(((△A∨～B)→△A)∧

(△A→(△A∨～B)))=

τn(((△A→△A)∧(～B→△A))∧

((△A→△A)∨(△A→～B)))=

τn((～B→△A)∧(△A→△A))=

τn(～B→△A)。

定义3.2A，B∈F(S)，规定ρn:F(S)×F(S)→[0，1]，则ρn(A,B)=1-ξn(A,B)，称ρn(A,B)为公式A与B的伪距离，(F(S),ρn)称为逻辑伪度量空间。

定理3.2A，B∈F(S),则ρn(△A，～B)=

1-τn(△A→～B)+1-τn(～B→△A)。

证明由定理3.1知ξn(△A，～B)=τn(△A→～B)+τn(～B→△A)-1，则

1-ξn(△A,～B)=

1-(τn(△A→～B)+τn(～B→△A)-1)。

得ρn(△A,～B)=

1-τn(△A→～B)+1-τn(～B→△A)。

4 小结

本文在值乘积命题逻辑系统中，给出了Goguenn值命题逻辑系统中命题公式的真度、相似度和伪距离的定义，证明了该真度的MP规则、HS规则及相关性质。在此基础上，可以继续深刻地研究近似推理等内容。