研究生综合素质模糊综合评价模型构建研究
——以延安大学为例
2021-04-12王小霞姜金平
王小霞,姜金平
(延安大学 数学与计算机科学学院,陕西 延安 716000)
研究生教育是培养高层次应用型人才的主要渠道之一。近年来,我国的研究生招生规模逐年扩大,研究生培养质量稳步提升。随着全国教育大会的召开,国家对研究生教育的重视也日益凸显。2020年9月30日,国务院学位委员会第三十六次会议审议通过《专业学位研究生教育发展方案(2020-2025)》指出,到2025年,以国家重大战略、关键领域和社会需求为重点,增设一批硕士、博士专业学位类别,将硕士专业学位研究生招生规模扩大到硕士研究生总规模的三分之二左右。延安大学是中国共产党创办的第一所综合性大学,现为陕西省政府与教育部共建大学,省级高水平建设大学和一本招生院校。延安大学的研究生教育历史可上溯到抗日战争时期,新世纪以来,延安大学的发展进入新的历史时期。1998年,经国务院学位委员会批准,学校获得硕士学位授予权,现已形成了学术学位、专业学位、同等学力人员申请硕士学位等多类型、较完整的学位与研究生教育体系,目前各类在校研究生2811人。学校现有哲学、应用经济学、政治学、马克思主义理论、中国语言文学、中国史、数学、物理学、化学、生物学、生态学、信息与通信工程、基础医学等16个硕士学位授权一级学科,课程与教学论、体育教育训练学等硕士学位授权二级学科,有法律、教育、翻译等9个专业学位类别,学科涵盖哲学、经济学、法学等10个门类。
随着研究生招生规模的不断扩大,如何进一步规范研究生培养机制,提高研究生培养质量,是当前研究生教育研究的一个热点问题[1-8]。本文借助模糊数学方法(Fuzzy Mathamatics Method),以延安大学为例,分析讨论了研究生综合素质评价模型构建问题。
1 预备知识
模糊综合评判的基本思想是利用模糊线性变换原理和最大隶属度原则,考虑与被评价事务相关的各个要素,对其作出合理的综合评价。
定义1[1]设A为给定论域U上的一个模糊模式,u1,u2,u3,…,un为U中的n个待识别对象,若A(ui)=max{A(u1),A(u2),…,A(un)},则称ui优先归属于模糊模式A。
定义2[1]设U,V为两个论域,对于一个模糊映射T:F(U)→F(V)若满足:对任意指标集I有T(∪i∈IλiAi)=∪i=IλiT(Ai),其中∀i∈I,λi∈[0,1],Ai∈F(U),则称T为模糊线性变换。即假设T为模糊映射,则对任意的λ∈[0,1];对任意的A∈ʃ(U),则有模糊线性变换T(λA)=λT(A)。
定义3[1]设与被评价的事物有关系的因素的个数为m个,记作U={U1,U2,U3,…,Um},则称U为因素集;设对评价事物做出的所有的可能出现的评语有n个,记作V={V1,V2,V3,…,Vn},其中Vi是定性描述的评语,则称V为评语集。
定理1[1]设R=F(U×V),TR为由R导出的模糊线性变换,则∀A∈F(U),有
(1)TR(A)=((A×V)R)V;
(2)TR(A)=∪λ∈[0,1]λTRλ(Aλ)。
2 模糊综合评价的基本步骤
模糊综合评价方法是依据模糊数学中模糊综合评判为基本模型的,将评价任务分解成多个评估模块,然后将每个模块再分解成若干问题,再将这些问题作为评价因素,构成单因素评价集,利用模糊值映射推导出模糊关系,确定因素重要程度模糊集和综合评价模型,得出综合评价。模糊综合评价主要有以下几个步骤。
2.1 单因素集和评价集
假设与被评价的事物间有关系的因素的个数为m个,则一级评价指标为U={U1,U2,U3,…,Um},由因素Ui确定对评语Vj的隶属度rij(i=1,2,…,m,j=1,2,…,n),将各一级评价指标继续分解,得到Ui的单因素集Ri={ri1,ri2,ri3,…,rin},即为隶属度集合,它是评价集的模糊子集。
假设对每一个单因素,其所对应的评语个数为n个,即将这些评语分为n个等级,则将这些评语组成的集合V={V1,V2,V3,…,Vn},称为单因素上的评价集。根据最大隶属原则,从评语集中取最大的结果作为评价结果。
2.2 构造模糊综合评价矩阵R
对每一个一级指标Ui(i=1,2,…,m),都有对应的Ri(i=1,2,…,m),将每一个Ui的Ri放在一起,则构成一个U×V上的评价矩阵
2.3 构建权重向量A=(a1,a2,a3,…,am)
在模糊综合评价中,各因素的权重确定的合理性直接影响评价结果。为了确定合理的权重指标,目前常用的方法有Delphi法(专家评议法)、专家调查法和求解模糊关系方程法。由于专家调查法在目前应用广泛,而且此方法比较简单直观,容易实现,因此,本文采用专家调查法来确定各评价因素的权重向量:A=(a1,a2,a3,…,am)。具体步骤如下:
(2)将所有专家的调查表数据汇总。如果各专家填写的调查表数据出入较大,则可反复进行调查,直到数据符合要求。
(3)计算因素Ui的权重系数ai。根据权重系数的计算公式
计算出Ui对应的ai。
2.4 构造模糊变换,确定综合评价模型,求出模糊综合评价集B
根据模糊线性变换原理,又因为权重向量A和综合评价矩阵R已知,将A和R进行合成运算,得到评价集V上的模糊综合评价集
B=A*R=
(b1b2b3…bn),
其中符号“*”表示模糊合成运算,
2.5 综合评价

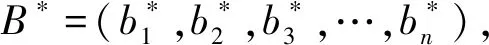
3 常见的模糊综合评价方法
(1)M(·,+)加权平均型
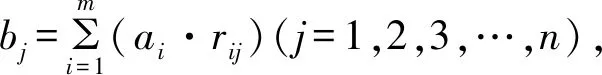
(2)M(∧,∨)主因素决定型
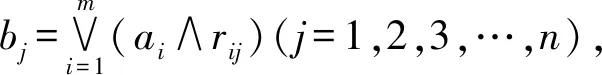
(3)M(·,∨)主因素突出型
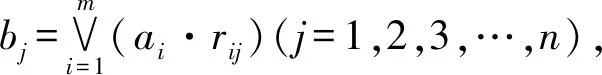
(4)M(∧,⊕)取小上界和型
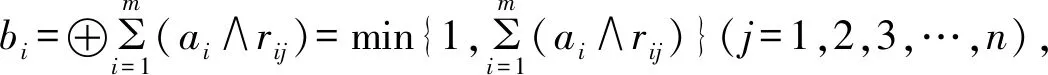
(5)M(乘幂,∧)全面制约型
(6)M(∧,+)均衡平均型

4 延安大学研究生综合素质评价指标体系
本文基于教育理论和我校研究生工作实践,将评价指标体系设计为2个等级,其中一级指标为考核指标,主要包括思想道德品质、学科专业基础、科研创新能力、社会实践能力和身心健康程度5项,主要考核研究生综合素质的总体情况。二级指标是考评指标,主要考评研究生思想道德、专业基础、科研能力和实践动手能力等,两方面指标各占一定比例,分层确定指标权重,具体见表1。
(1)一级指标:思想道德品质。二级指标:评价研究生是否具有坚定的政治方向和延安精神特质,以及研究生思想意识、理论素养和法制观念、社会公德、个人品质等。
(2)一级指标:学科专业基础。二级指标:评价研究生学习态度、学科专业知识掌握程度、学习成果完成情况,主要包括课堂表现、课程学习情况、专业基础和知识扩展情况。
(3)一级指标:科研创新能力。二级指标:评价研究生创新意识、学习成果数量和等级,主要包括参与学术交流情况、主持科研项目、发表学术论文情况、获奖情况。
(4)一级指标:社会实践能力。二级指标:评价研究生社会责任感、社会活动参与度以及社会荣誉感等。对研究生的组织协调能力、解决问题能力进行分析评价。
(5)一级指标:身心健康程度。二级指标:评价研究生的身体健康程度及心理健康程度,是否具有健康的体魄和良好的心理调节能力、心理承受能力。
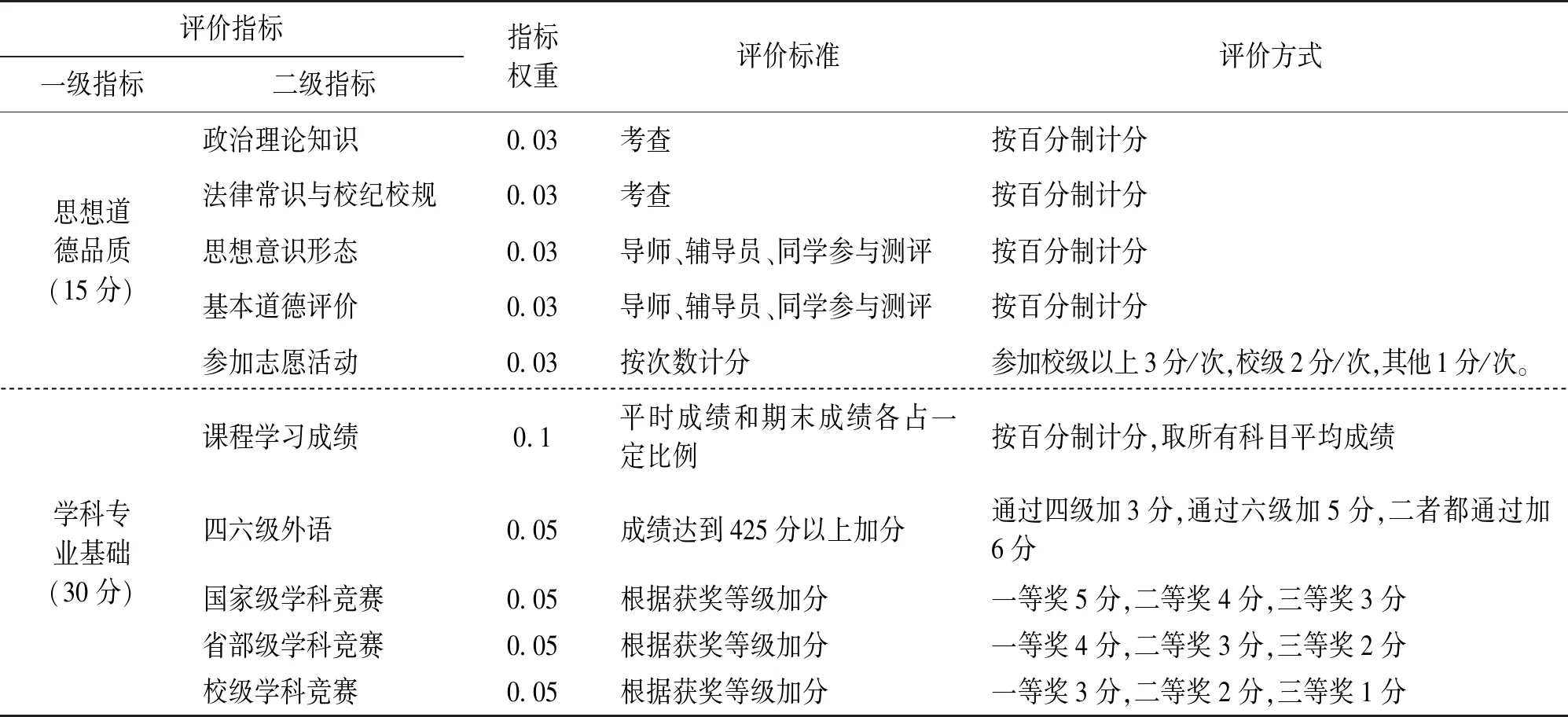
表1 延安大学研究生综合素质评价体系表
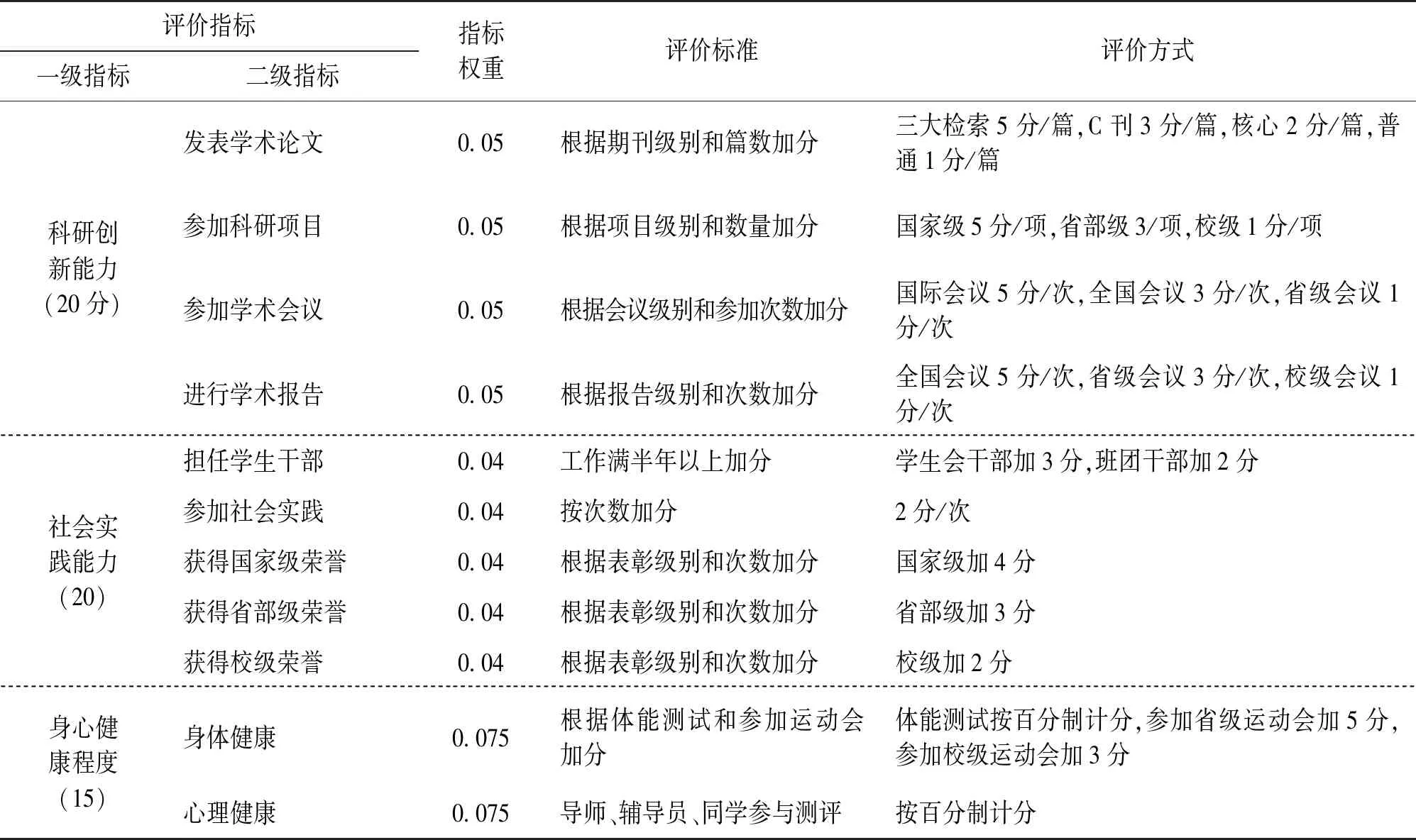
续表1
5 研究生综合素质评价模型
综合评价是对受到多个因素制约的事物或对象作出一个总的评价。在日常生活中,如产品质量评定、科技成果鉴定等都属于这类问题。由于从多方面对事物进行评价难免带有模糊性和主观性,所以采用模糊数学方法进行综合评价会使结果尽量客观,从而取得良好的实际效果。
一般来讲,模糊综合评价的数学模型分为一级模型和多级模型2种,本文中主要采用一级评价。根据前面分析,选取我校2019级数学一级学科15名研究生,对其各项评价数据进行调查统计,用于估算模型和验证其合理性。
1)设计评价指标集
我校研究生综合素质评价共有5项一级指标,可设综合素质评价集
V={V1,V2,V3,V4,V5}={思想道德素质,学科专业基础,科研创新能力,社会实践能力,身心健康程度}。
2)调查统计评价数据(见表2)
3)确定评价指标权重
根据专家评价法确定各评价因素的权重如下:
W=(0.15,0.3,0.2,0.2,0.15)。
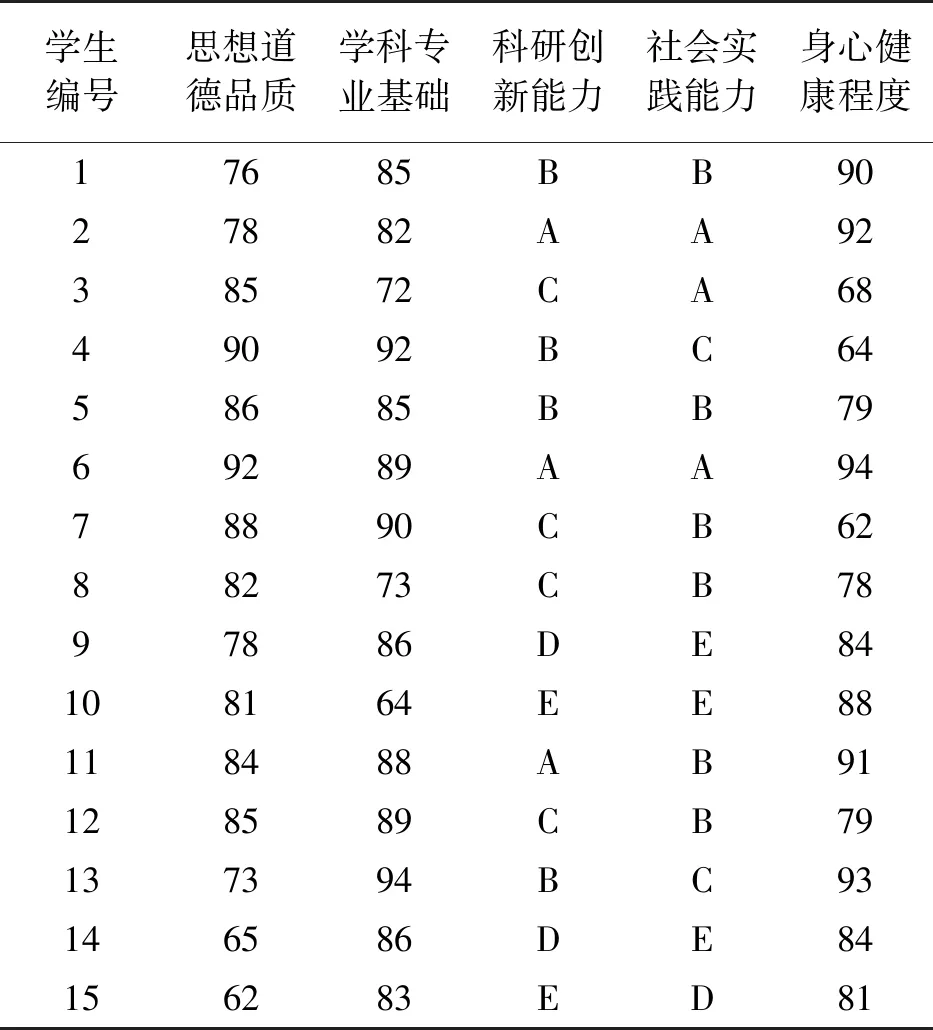
表2 延安大学研究生综合素质调查统计表
4)建立评价等级集合:V=(优秀,良好,中等,合格,不合格),其中思想道德品质、学科专业基础、身心健康程度的优秀为“xi≥90”,良好为“80≤xi<90”,中等为“70≤xi<79”,合格为“60≤xi<69”,不合格为“xi<60”;科研创新能力、社会实践能力的优秀为“A”,良好为“B”,中等为“C”,合格为“D”,不合格为“E”。
5)建立模糊评价矩阵。设一级指标思想道德素质、学科专业基础、科研创新能力、社会实践能力、身心健康程度所对应的单因素评价集分别为R1,R2,R3,R4和R5,则根据调查统计表可得
从而综合评价矩阵R矩阵可表示为

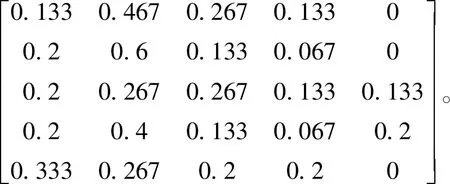
6)利用模型(1)M(·,+)加权平均型建立模糊综合评价矩阵
S=W∘R=(0.15,0.3,0.2,0.2,0.15) ∘

(0.2099,0.4235,0.18995,0.11005,0.0666)。
由此可知,20.99%的研究生综合素质为优秀,42.35%的研究生综合素质为良好,18.995%的研究生综合素质为中等,11.005%的研究生综合素质为合格,6.66%的研究生综合素质为不合格。
7)利用模型(2)M(∧,∨)主因素决定型建立模糊综合评价矩阵
S=W∘R=(0.15,0.3,0.2,0.2,0.15) ∘

(0.2,0.3,0.2,0.15,0.2)。
进行归一化处理,可得S=W∘R=(0.2/1.05,0.3/1.05,0.2/1.05,0.15/1.05,0.2/1.05)=
(0.19,0.286,0.19,0.144,0.19)。
可知,19%的研究生综合素质为优秀,28.6%的研究生综合素质为良好,19%的研究生综合素质为中等,14.4%的研究生综合素质为合格,19%的研究生综合素质为不合格。
8)利用模型(3)M(·,∨)主因素突出型建立模糊综合评价矩阵
S=W∘R=(0.15,0.3,0.2,0.2,0.15) ∘

(0.06,0.18,0.0534,0.03,0.04)。
进行归一化处理,可得
S=W∘R=(0.06/0.3634,0.18/0.3634,
0.0534/0.3634,0.03/0.3634,0.04/0.3634)=
(0.165,0.495,0.147,0.083,0.11)。
可知,16.5%的研究生综合素质为优秀,49.5%的研究生综合素质为良好,14.7%的研究生综合素质为中等,8.3%的研究生综合素质为合格,11%的研究生综合素质为不合格。
比较模型(1)、(2)、(3)可知,3种运算结果基本一致,可以看出我校研究生综合素质总体较好,良好等次以上占50%左右,其中加权平均型充分考虑到各因素影响,因此在具体评价过程中建议优先采用。
