高射速自动机气液式缓冲装置仿真分析
2021-04-12徐亚凯杨宏亮殷鹏贤
徐亚凯,杨宏亮,殷鹏贤,陈 雷
(中国船舶集团有限公司第七一三研究所,河南郑州450015)
0 引 言
目前,减小武器后坐力的方法主要有软后坐技术(前冲技术)、无后坐技术、后坐缓冲装置、炮口制退器等。高射速小口径火炮武器目前多采用弹簧作为缓冲装置,其结构简单,生产及使用维护方便,可靠性高。但受弹簧力学特性限制,该种缓冲方式下后坐阻力只能随后坐位移增加来降低,而速射炮为保证供弹可靠性对后坐位移严格控制在一定范围内,导致降低最大后坐阻力比较困难。虽然后坐阻力的大小对于舰艇类武器平台影响不大,但对于飞机和车辆等承载平台影响十分明显。降低火炮最大后坐阻力,对于车辆飞机等移动平台具有重要意义。因此,为提升武器的适装性,就必须进一步降低后坐力。
小口径火炮反后坐方式有弹簧式、簧液式和气液式等,目前研究方向主要集中在簧液式和气液式。文献[1]分析了最佳后坐力控制(FORC)原理特性,验证了其可行性;文献[2]对3种缓冲装置运用键合图理论建立了动力学模型并进行了仿真比较,结果显示内源式FORC装置效果最明显;文献[3]对气液式缓冲器的刚度、阻尼和预压等关系进行了研究,为缓冲器参数优化提供了参考依据;文献[4]采用湍流模型的计算方法对气液式缓冲装置进行分析,并探讨了温度对缓冲装置的影响;文献[5]提出采用FORC理论对高射速自动机后坐力进行控制并开展了试验。
可以看出,尝试利用气液式缓冲器代替弹簧式缓冲器是后坐力控制研究的趋势,本文以小口径火炮为研究对象,通过数值仿真与流体仿真相结合,验证气液式缓冲器的反后坐效果。
1 工作原理
气液缓冲反后坐装置的原理图如图1所示。图中,从左往右分别是:前缓冲簧、主活塞,液腔1,液控阀,液腔2,气液活塞和气腔。当火炮击发后,火炮后坐部分带动主活塞一起后坐。在主活塞的作用下,液腔1的压力升高,液体经过液控阀进入液腔2,此时,液控阀流液面积较大,后坐阻力小。流入液压腔的液体带动气液活塞运动,压缩气压腔中的气体,存储部分能量。随着两侧液腔压力的变化,流液孔面积动态变化。复进时,在气压腔气体压力作用下,气液活塞运动,液压腔中的液体带动后坐部分复进,此时,液控阀流液面积小,复进阻力大。复进到位或过位时,连接筒前端与前缓冲簧作用,避免刚性碰撞,保护机构安全。
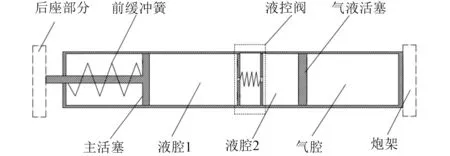
图1 气液缓冲装置结构示意图Fig.1 Structural representation of the gas-liquid buffer device
2 运动方程
后坐运动微分方程可表示为:
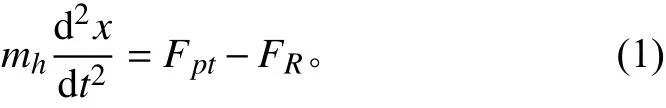
其中:Fpt为炮膛合力;FR为后坐阻力。
气液缓冲式自动机后坐过程中主要承受液压阻尼力、气腔阻力和摩擦力,因此,后坐阻力可以表示为:
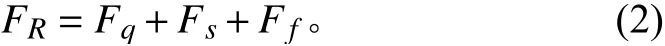
其中:Fq为气腔阻力;Fs为液压阻力;Ff为摩擦阻力。气腔压力可表示为:
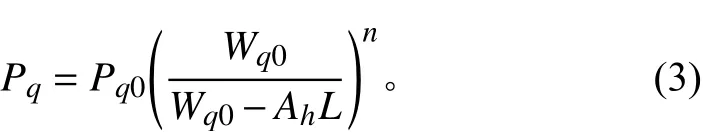
其中:n为绝热指数,取n=1.4;L为主活塞后坐位移;Ah为主活塞面积;Wq0为气液活塞初始体积;Wq为气腔实时体积。
液压阻尼力计算公式如下:

其中R为后坐时总的液压阻尼系数。
炮膛合力的计算公式可以表示为:
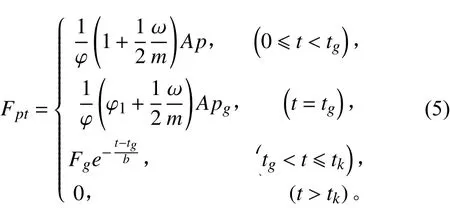
式中:φ为次要功计算系数;φ1为仅考虑弹丸旋转和摩擦2种次要功的计算系数;m为弹丸质量;ω为火药装药质量;A为膛内导向部分的横截面积;p为膛内平均压力;pg为tg时刻的膛压;Fg为tg时刻的的炮膛合力;b为反映炮膛合力衰减快慢的时间常数。
3 数值仿真计算
分别对弹簧式和气液式缓冲器进行仿真计算,对比2种形式缓冲器的反后坐效果。
根据上节公式,缓冲器后坐阻力可以根据后坐位移和速度求出,因此,在此采用数值方法求解,数值方法采用Runge-Kutta方法。采用4阶Runge-Kutta方法,其公式为:
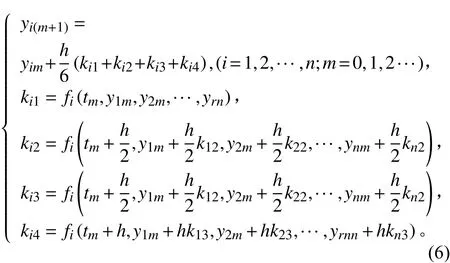
式中h=tm+1−tm为积分步长。
高射速自动机发射频率可达4 000次/m in以上[5],计算取值4000次/m in,参考某内弹道数据,进行数值仿真计算。
1)弹簧式缓冲器数值仿真
采用圆柱压缩弹簧作为缓冲装置时,后坐阻力主要包括弹簧力和摩擦力,根据以上公式编制程序进行仿真计算,其后坐位移及后坐力结果如图2和图3所示。
通过仿真结果可以发现,采用弹簧式缓冲器,最大后坐位移约为15.5 mm,最大后坐力约为61.1 kN。
2)气液式缓冲器数值仿真
采用气液缓冲反后坐装置时,根据以上公式编制程序进行数值仿真。气液缓冲器为两侧对称布置,因此仅需计算单侧缓冲器。设置初始条件为:气压腔初压7MPa,活塞摩擦力取为500 N,进行仿真计算,其后坐位移及后坐力结果如图4~图6所示。

图 2弹簧缓冲器后坐位移变化曲线Fig.2 The variation curve of the recoil displacement w ith time for spring buffer device
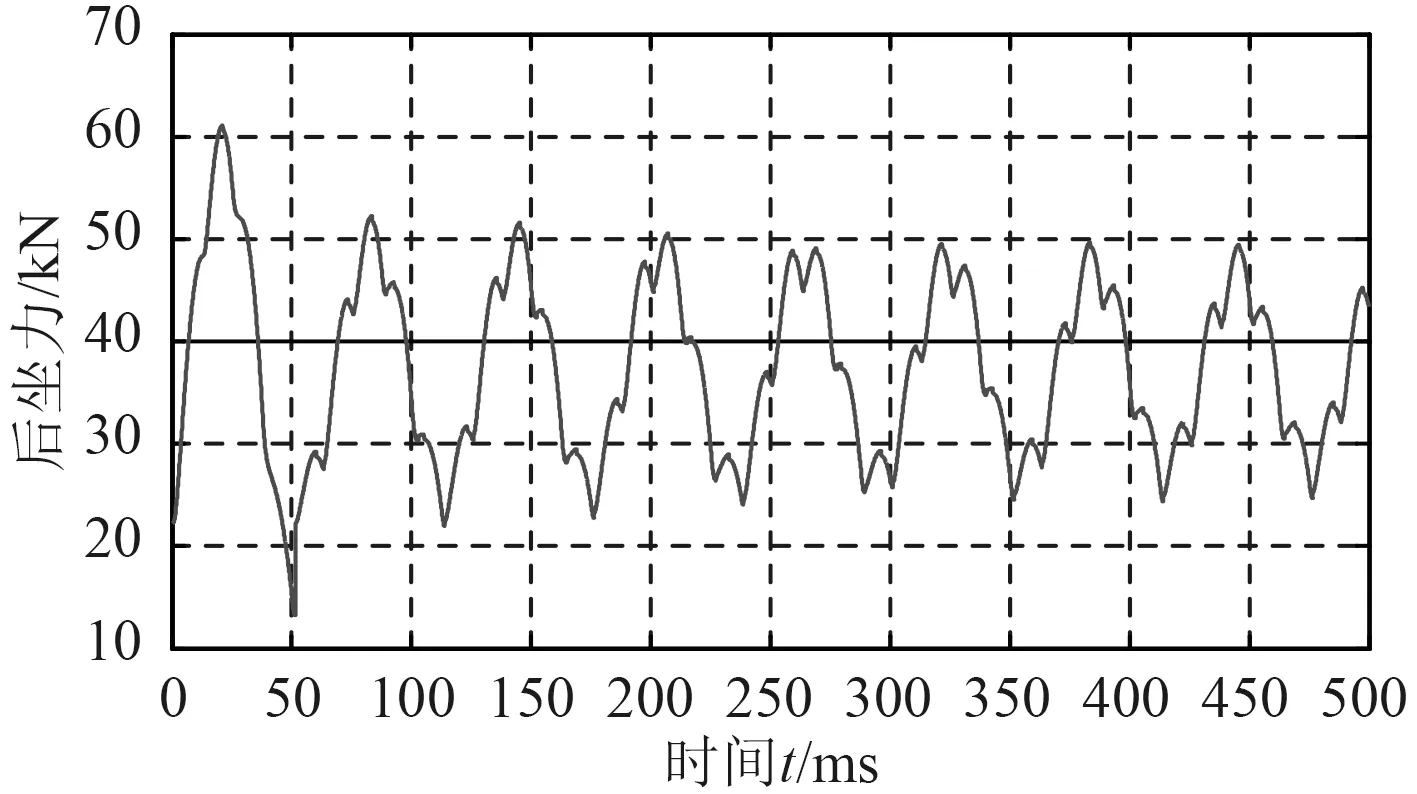
图3 弹簧缓冲器后坐力变化曲线Fig.3 The variation curve of the recoil forcew ith time for spring buffer device
图4 气液缓冲器后坐速度随时间变化曲线
Fig.4 The variation curve of the recoil speed w ith time for
gas-liquid buffer deviceby numerical simulation
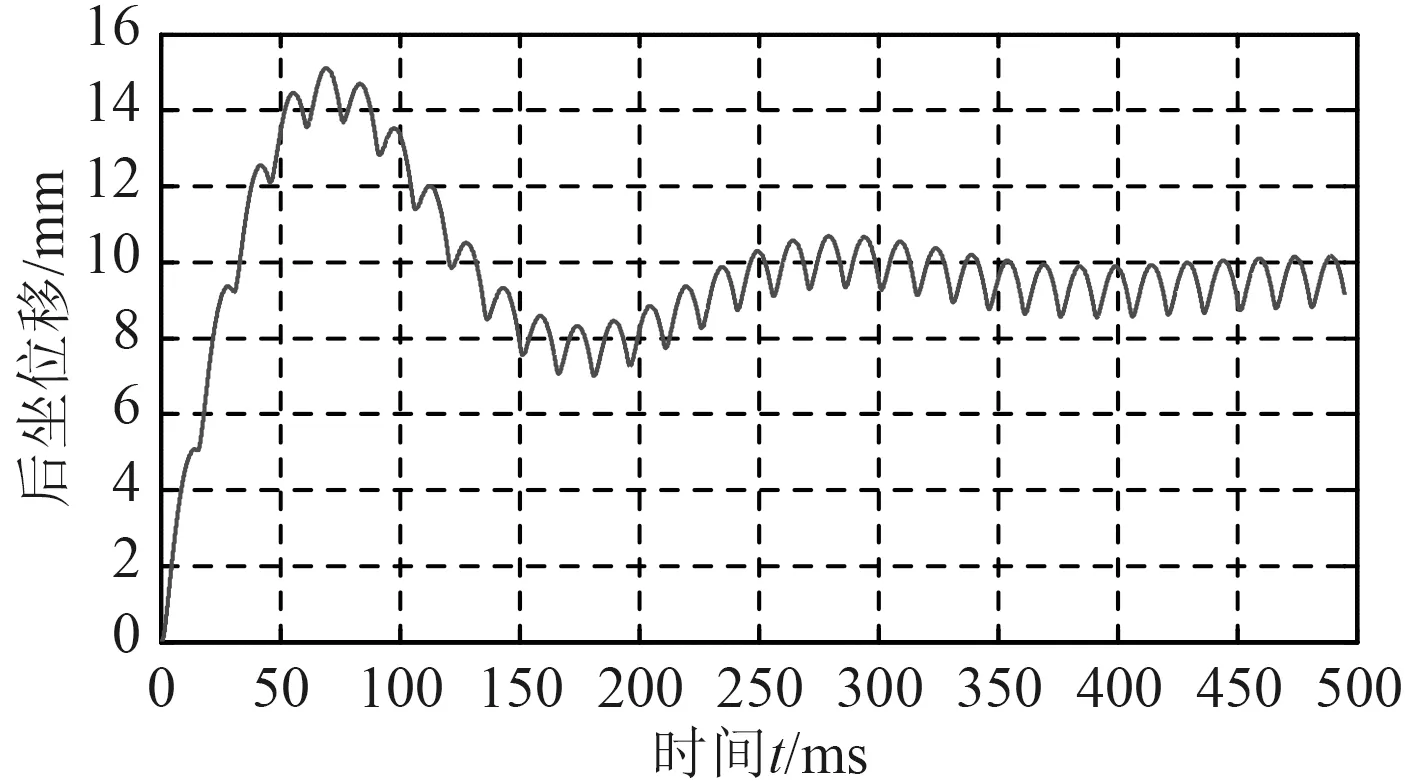
图5 气液缓冲器后坐位移随时间变化曲线Fig.5 The variation curve of the recoil displacement w ith time for gas-liquid buffer device by numerical simulation
通过仿真结果可以发现,选取合理的参数,采用气液缓冲器,在长连发仿真过程中,后坐速度最大值为0.61m/s;后坐位移最大值15.1mm,并在10mm附近进行浮动射击。整个射击过程中,单个缓冲器后坐力最大值为18.5 kN。缓冲装置为2个并列安装,因此经过气液反后坐装置,火炮总体后坐力降低为37 kN。相比使用弹簧式缓冲器61.1 kN的后坐力值,气液缓冲装置极大降低了火炮的最大后坐力,后坐力降幅达39%,效果十分明显。
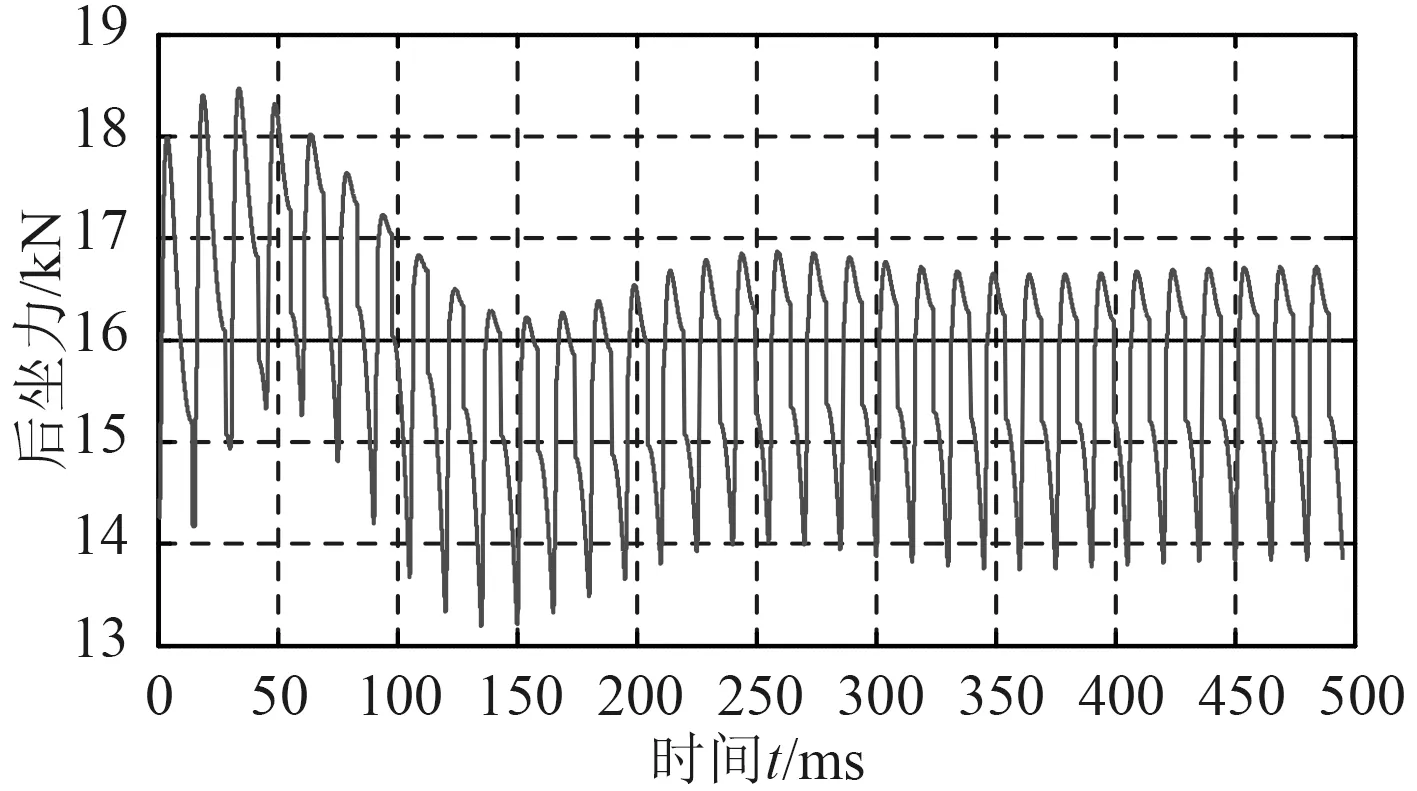
图6 气液缓冲器后坐力随时间变化曲线Fig. 6 The variation curve of the recoil force with time for gas-liquid buffer device by numerical simulation
4 流体仿真
为进一步验证气液缓冲装置反后坐效果,利用流体仿真分析软件进行计算,获取与数值仿真相同参数条件下的后坐力、后坐速度和后坐位移变化曲线,并进行对比分析,气液缓冲器流场模型如图7所示。

图7 气液缓冲器流场模型图Fig.7 The flow field model of gas-liquid buffer device
一个发射周期内压力云图变化如图8所示。
后坐速度、后坐位移及后坐力曲线如图9~图11所示。

图8 气液缓冲器一个发射周期内压力云图Fig.8 The variation of pressure for gas-liquid buffer device in a cycle
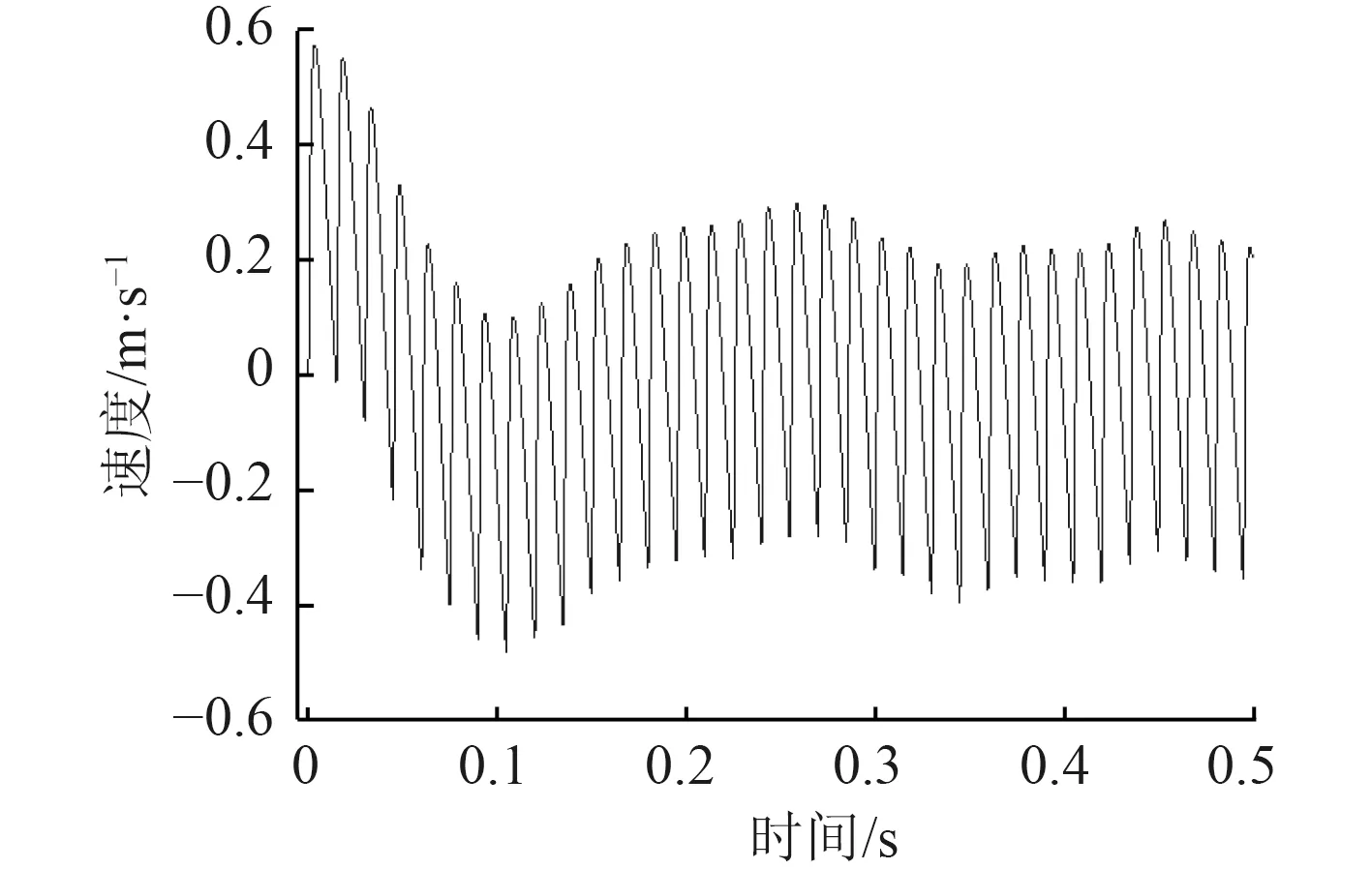
图9 气液缓冲器后坐速度变化曲线Fig.9 The variation curve of the recoil speed w ith time for gas-liquid buffer device by fluid simulation
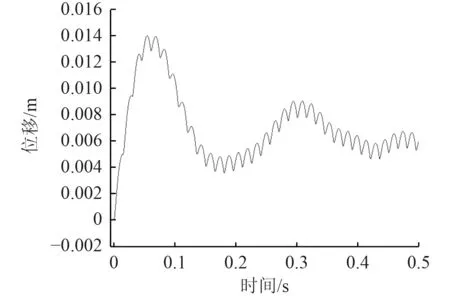
图10 气液缓冲器后坐位移变化曲线Fig.10 The variation curve of the recoil displacement w ith time for gas-liquid buffer device by fluid simulation
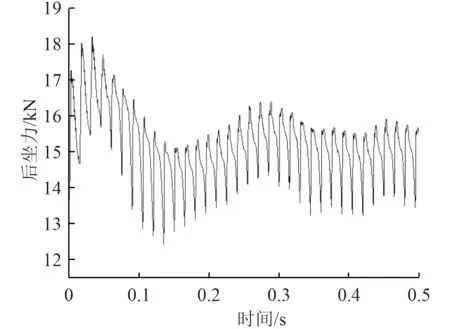
图11 气液缓冲器后坐力变化曲线Fig.11 The variation curve of the recoil force w ith time for gas-liquid buffer deviceby fluid simulation
通过仿真结果可以发现,在长连发仿真过程中,后坐速度最大值为0.57m/s;后坐位移为13.9mm;整个射击过程中,单个缓冲器后坐力最大值为18.2kN。
数值仿真与流体仿真对比结果如表1所示。可知,数值仿真与流体仿真结果较为接近,误差小于10%,进一步验证了仿真结果的准确性。

表1 数值仿真与流体仿真对比结果Tab.1 The comparison of numerical and fluid simulation
5 结语
本文在理论分析的基础上,对缓冲装置进行了数值仿真与流体仿真。仿真计算结果表明,该装置结构合理,降低后坐力效果明显,在高射速武器上具有很好的应用价值和前景。
