GeoGebra软件在电磁场实验的应用

黄闽海

（福建技术师范学院 电子与机械工程学院，福建 福州 350300 ）

GeoGebra是一款动态数学软件,将图形、代数和数据表动态结合，由于其界面的简洁性、易操作性、动态可视性，现已在世界各地的课堂上得到越来越广泛的应用，取得了丰硕的成果.源于以上诸多优点，GeoGebra（以下简写为GGB）在电磁学理论的教学演示、实验数据处理、仿真实验、辅助解题等方面所具有的优越性值得深入研究[1].

传统的电磁学实验，通常采用手工方法进行实验数据的处理，存在描点不准确、绘图比例不当等缺点，造成人为误差，导致所得结果的精度不理想，难以满足实验的要求[2-3].本文基于GGB 软件，在电磁学实验前，对试验结果进行预演，将电场、磁场物理量的表达式转换成形象直观的几何曲线；在实验数据处理阶段，利用GGB 的绘图功能将试验数据拟合成图形，并从拟合图形中获取相关物理量的数学方程，从而方便将理论数据与实验结果进行比对，验证实验的准确性.通过GGB 软件的辅助，可极大地减小实验数据的处理难度，节约计算时间，更准确地绘制出电、磁场分布曲线.

1 GeoGebra 应用于静电场等势面的测量实验

1.1 静电场的理论依据

静止电荷产生的电场称为静电场.两根长同轴圆柱面间的电势分布是静电场描绘的经典实验.由电磁场理论可知，恒定电流的电场和相应的静电场的空间形式是一致的[4].只要电极电势不变，电极形状一定，空间介质均匀，在任意考察点，均有U恒定=U静电或E恒定=E静电[5].基于此，以同轴圆柱间的“静电场”来研究电势分布（图1）.半径为a 的圆柱导体A 和半径为b 的圆柱壳导体B 同轴放置，分别带等值异号电荷，A 和B 间为真空，由高斯定理可知，其电场线沿径向由A 向B 辐射分布，其等势面为一簇同轴圆柱面.因此，只要研究任一垂直轴的横截面上的电势分布，通过正交法即可知道电场的分布.设A（或B）的电荷线密度为λ，由高斯定理可得：E=λ/2πε0r.

两圆柱面之间任意半径为r 的一点电势为

令r=b 时，Ub=0，则有

代入公式（1）得:Ur=Ualn，可导出等势线半径r 的表达式为r=an×b1-n，式中n=Ur/Ua.

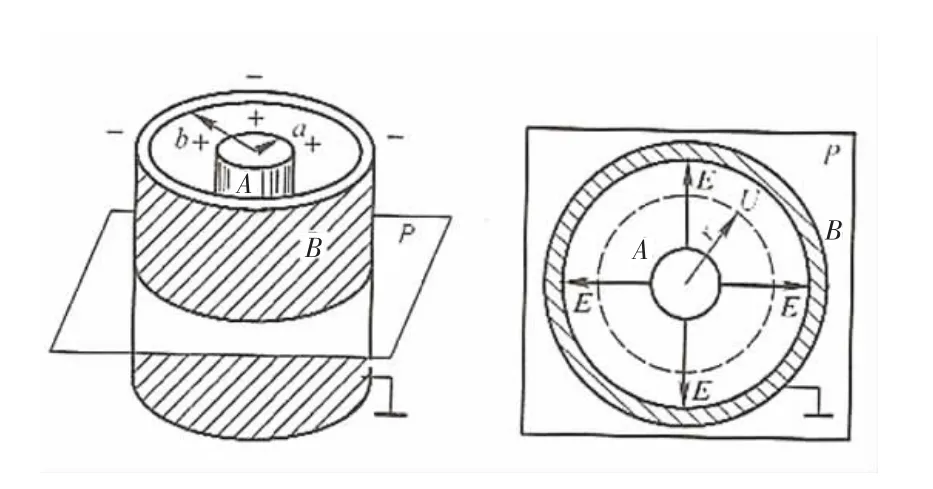
图1 同轴圆柱间的静电场

1.2 用GeoGebra 绘制等势线

打开GGB，建立2 个滑动条a、b，代表同轴的两个半径，a 的取值范围为[0.5,1]，步进设置为0.05，b的取值范围为[6,9]，步进设置为0.1.接着在代数区输入等势圆半径r 的方程f(x)=axb1-x，x 轴代表测量点电压与圆柱面之间所加的电压之比n.

在绘图区输出等势线半径变化的曲线（图2），调整xy 轴的比例使x 轴的刻度以0.1 为网格单位显示出来，选择描点工具开启对齐到网格的功能，可以很容易地捕捉到x 轴上以0.1 为步进的r 曲线上的点A、B、C,…,J，共9 个点，输入两个同轴圆柱的具体半径，以实验仪器中a=0.75 cm，b=7.5 cm，UAB=10 V为例，在代数区ABC 各点的纵坐标就是各个等电势圆的半径数值，用“R 理论”来表示，见图2 左侧，各点的半径分别为5.96、4.76、3.76、2.99、…，将其填入图6 中的GGB 表格区的“Ur”和“R 理论”列中.如果拖动滑动条，使a、b 在其取值范围间变化，对应的曲线亦随之变化，可以直观方便地演示等势圆半径变化规律，在绘图区中能动态地观察到各个捕捉点的y 轴坐标的变化，在教学中起到示范和引导作用.

以A、B、C,…,J 各点的纵坐标值为半径，绘制出一系列同心圆，每个圆之间的电势差为0.1Ua，两同轴间的电压以10 V 为例，绘出了在理论上间距为1 V 的等势线簇（图3）.

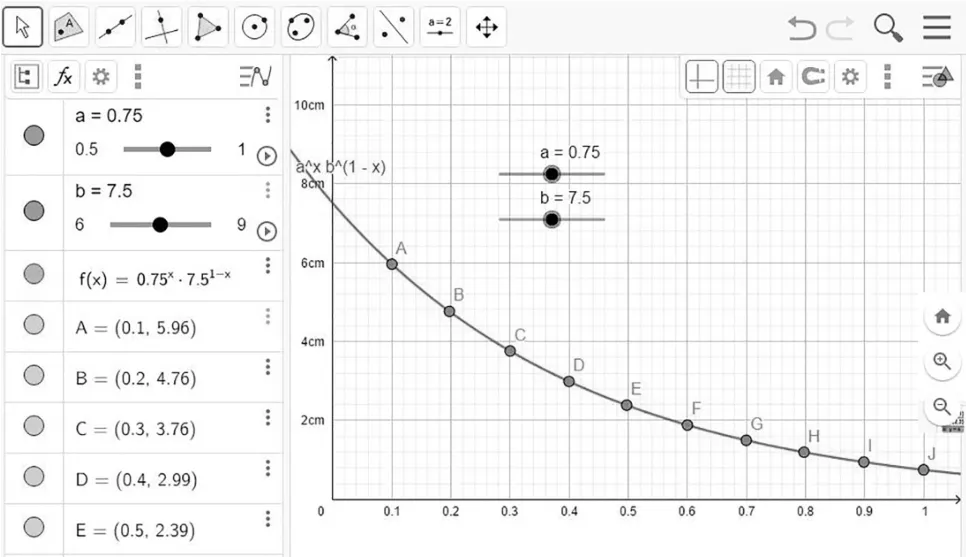
图2 绘制等势线半径随n=Ur/Ua变化的曲线

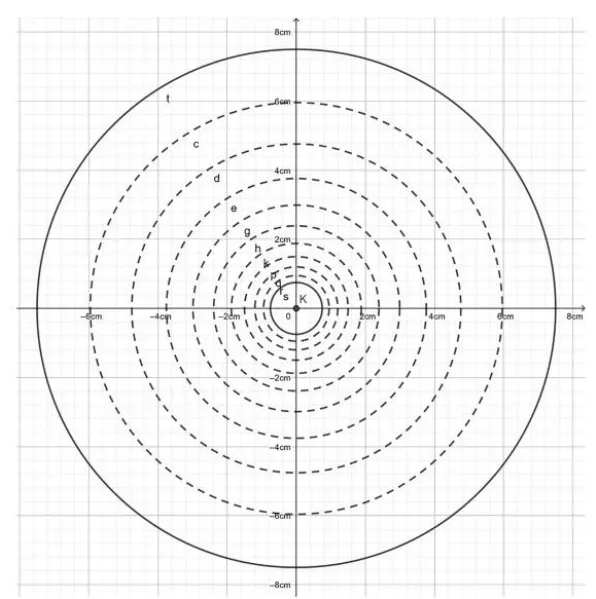
图3 GGB 绘制理论上的等势线簇

1.3 实验测量

两层静电场测绘仪如图4 所示.导电物质是一种导电玻璃，玻璃表面均匀地涂一层薄石墨粉，其导电率极低，符合模拟条件.仪器左下边测绘的是模拟等值异号点电荷的等势线簇，右下边测绘模拟同轴圆柱带电体的电场.将接线柱分别与电池的正极和负极相连，建立一个恒定电流场，从而形成一组等势线，电场中各点的电势通过双层同步探针和灵敏电压表测出.为方便测量和计算，将两接线柱的输入电压调节为直流10 V，仅以同轴圆柱的静电场为例.

1）连接好设备，下探针测量电场某点的电势，上探针适当用力在绘图纸上打出同步点.

2）测绘同轴电缆的等势线簇.取U=2,3,…,9 V 共8 组，每组8 点，大致分布在8 个方位上.

图4 两层静电场测绘仪

1.4 基于GGB 的数据处理

在绘图纸上放一只直尺，拍摄后将照片导入到GGB，将直尺的长度与绘图区的坐标轴长度相比较，算出图像的放大系数n；利用“位似工具”选择导入的图片，在弹出的缩放比例对话框中填入1/n，这样图片尺度与GGB 坐标尺度为1∶1 的关系，这点非常重要，决定了在GGB 中测量出来的等势线的尺寸与实际的打点绘图尺寸能否相符.图5 是将一系列实验打出的等势点导入到GGB 中的情况，可以看出直尺的刻度与下方的绘图区坐标已处理为1∶1 的关系.

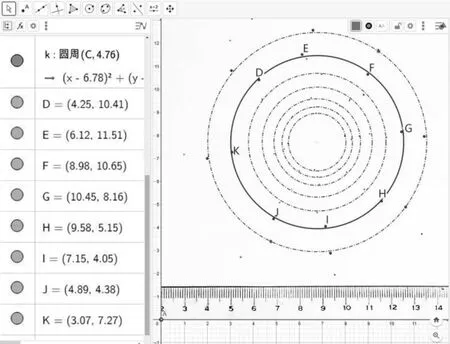
图5 将实验打点图导入GGB 处理

将图片锁定到坐标轴上，通过鼠标滚轮的上下滚动，可以无极缩放图片（与坐标轴联动），这样就可以精细地处理各系列的等势点，这是手工绘制所无法比拟的优势.利用“描点工具”将各打点映射到坐标系中，对某一等势线上的点，如图5 中的D、E、F、G、H、I、J、K 共8 个点，用圆形拟合工具绘制出最恰当的圆，以保证圆心位置误差及其对应的半径标准差均为最小，即为“优质组合[6]”.在图5 左边的参数区可以查看到该圆的代数方程为（x-6.78）2+（y-7.71）2=22.66，将22.66 开根号，得到的数值就是这条等势线的半径值.用同样的方法可以得出一系列等势线半径数值，用“R 实验”来表示，也填入到GGB 的表格区（图6左方表格的B 列）.

1.5 基于GGB 的实验误差分析

通过理论计算和实验的打点拟合，获得了一组等势圆半径的理论值和实验测量值，再对数值进行自然对数运算，得到对应的“ln R 理论”值和“ln R 实验”值，如图6 左方所示.

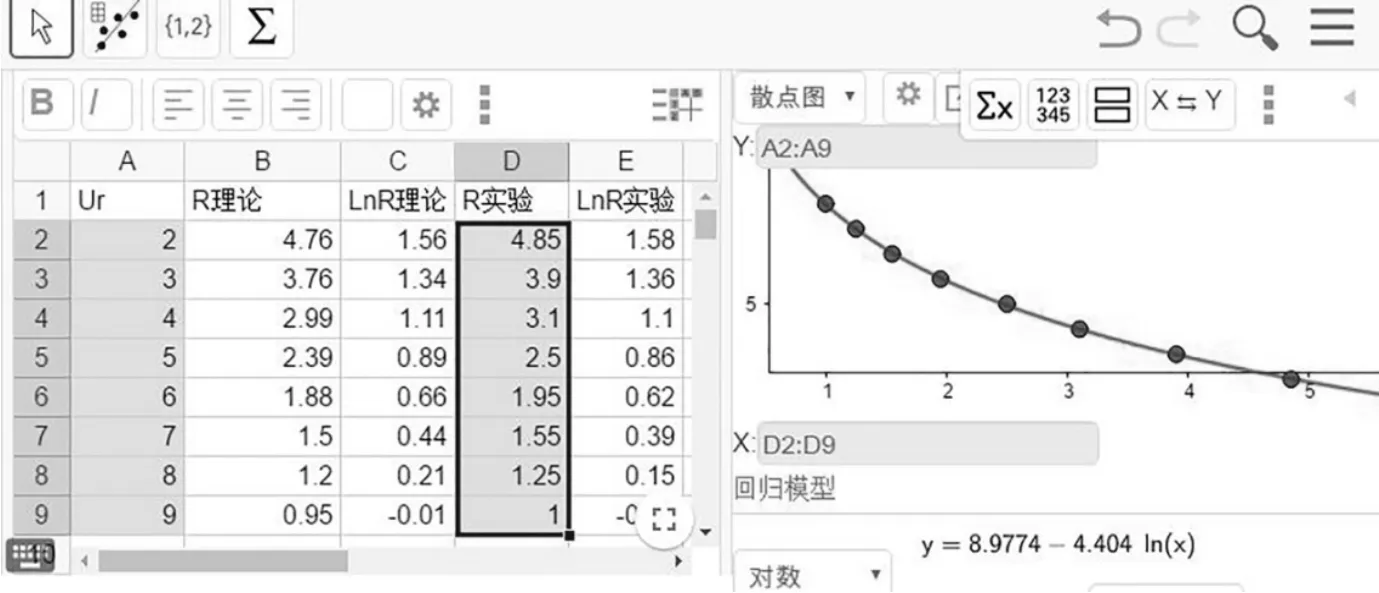
图6 等电势圆半径R（理论值、测量值）及对应对数值列表、R 实验值的拟合曲线

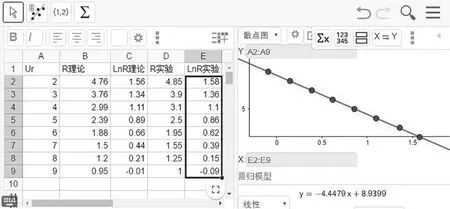
图7 Ur-ln R 实验的线性拟合曲线

表1 4 个拟合方程及系数误差

2 GeoGebra 应用于通电螺线管轴线上磁场的测量实验

2.1 螺线管轴线上的磁感应强度

本实验是利用霍尔效应测量磁感应强度B 的磁场分布.利用毕奥-萨伐尔定律推导磁感应强度的表达式[7]，对于长度为2L、匝数为N、半径为R 的螺线管，在离开中心点x 处的磁感应强度的分布公式为：

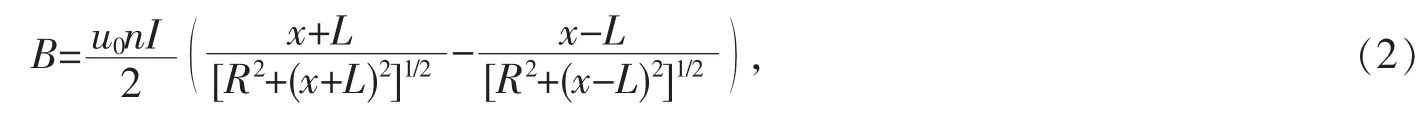
式中：u0为真空磁导率；n=N/2L，为螺线管单位长度的匝数；本实验的螺线管匝数为1 810 匝；长度2L 为181 mm；螺线管半径为21 mm.对于“无限长”螺线管，L>>R，B=μ0nI；对于“半无限长”螺线管,在端点处有x=L，B=μ0nI/2.

2.2 用GeoGebra 绘制通电螺线管中轴线上的磁感应强度B

令K′=μ0nI/2，在GGB 中创建滑动条d，表示螺线管的长度的一半；创建滑动条R，表示螺线管的半径.在函数区输入磁感应强度的分布方程f(x)（图8），播放滑动条d 或者R，在右侧绘图区即会动态显示磁感应强度曲线随螺线管长度或半径变化的情形.将d、R 分别固定为实验的实际参数90.5、21 mm，令K=1/2，即等式两边同时除以μ0nI，即有限长螺线管与无限长螺线管在轴线上的磁感应强度之比.捕捉曲线与Y轴的交点A，可以看到其坐标为（0,0.97），表明在该螺线管中轴线上中点的B 值是无限长通电螺线管的B值的0.97 倍；捕捉螺线管端点M，坐标为（-90.5,0.5），表明螺线管端口的B 值等于无限长通电螺线管的B值的一半.

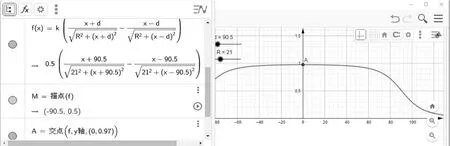
图8 用GGB 仿真的螺线管中轴线上磁感应强度分布图

2.3 实验原理

实验采用霍尔效应法对通电螺线管的磁感应强度进行测量，霍尔效应其实质是运动的带电粒子在磁场中受洛仑兹力的作用而引起的偏转.一般用掺杂的N 型半导体作为霍尔元件，载流子为电子，被约束在固体材料中，这种偏转将导致在垂直于电流和磁场的方向上产生正负电荷在不同侧的聚积，从而形成附加的横向电场.当载流子受到的洛伦兹力fL=-fE时（fE为附加横向电场力），载流子积累便达到动态平衡.这时在A、B 两端面之间建立的电场称为霍尔电场EH，相应的电势差称为霍尔电势VH.

通过推导可知霍尔电势计算公式：VH=KHISB，KH为霍尔元件的灵敏度，它是反映材料霍尔效应强弱的参数，由制造商提供数值，IS是霍尔元件的工作电流.本实验就是通过测量螺线管轴线上各处的霍尔电势VH，计算出对应点的磁感应强度B，从而描绘出螺线管轴线上的磁感应强度分布曲线.

2.4 实验方法与实验数据

实验仪器为ZC1510 型螺线管磁场测定仪，将霍尔效应测试仪与霍尔效应实验架连接，将螺线管线圈的励磁电流IM的直流恒流源设置为500 mA，螺线管就产生一个恒定的磁场；供给霍尔元件的工作电流IS设置为5.00 mA，测量从螺线管中心位置到螺线管外25 mm 之间的不同位置的VH值，以螺线管中心为x 轴0 点，间隔5 mm 测量一次.每个点测量时分别通以正、反向的励磁电流和霍尔元件工作电流，共测量4 次霍尔电势VH，然后取平均值，这样可以消除一部分系统误差[8].表2 是一组学生实验数据，VH为平均值.

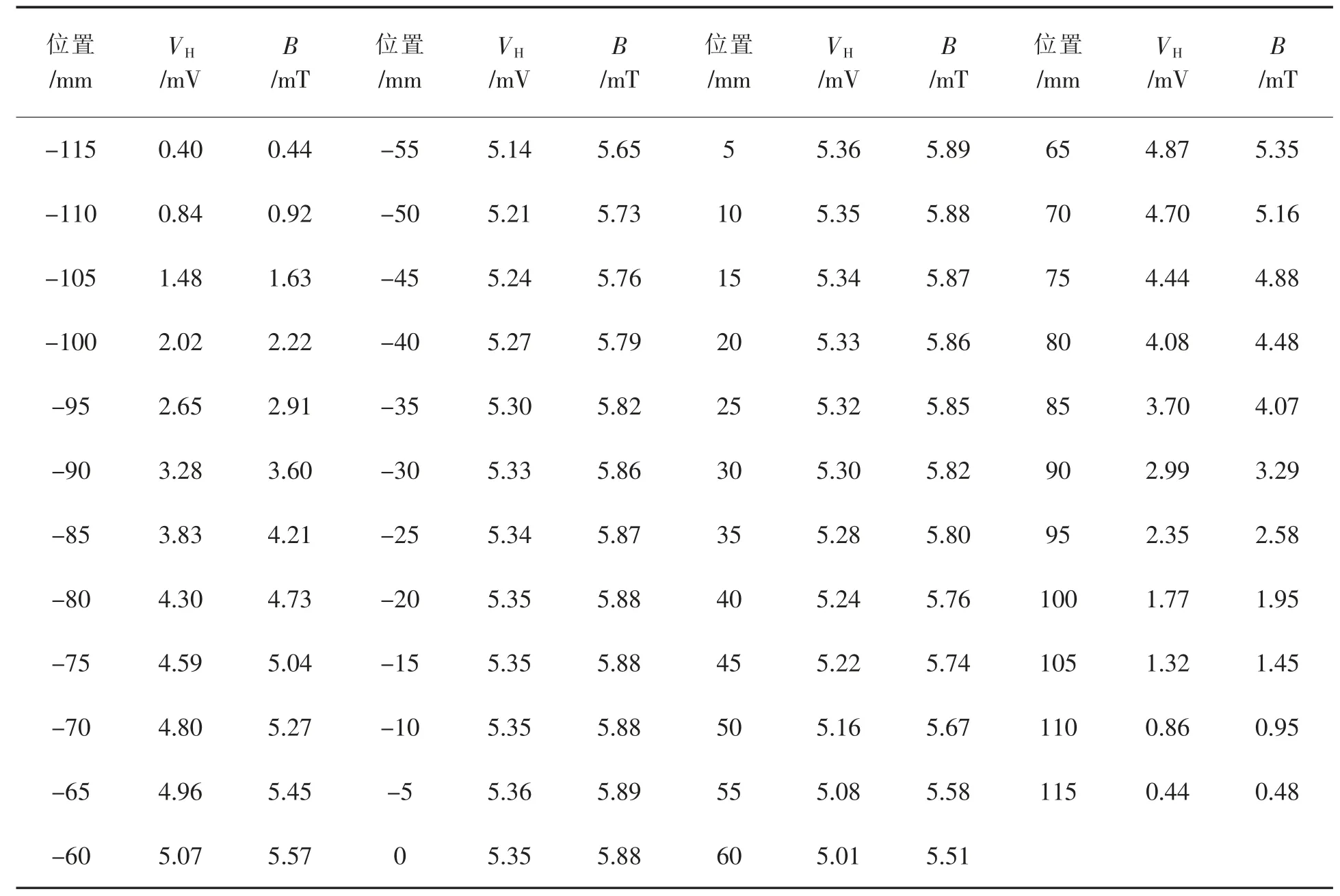
表2 实验测量的直螺线管中轴线上的霍尔电势值、磁感应强度值（IM=500 mA IS=5 mA KH=182 mV/mAT）

2.5 实验数据处理

在GGB 软件表格区中，将坐标x 和对应的B 输进表格，对x 和B 进行“双变量回归分析”，在表格区生成散点图，图9 中圆点表示实验测量数据，勾选“线图”将散点连成一条平滑的拟合曲线.从图中看到，实验测量数据点都落在拟合曲线附近，拟合结果良好，即可得到螺线管中轴线上磁感应强度分布图，与绘图区生成的相同螺线管参数的理论分布曲线进行粗略比较，图像相似，由于没有进行叠加比较，无法观察到具体的偏差.点击输出按钮，选择“将图像复制到绘图区”，在图10 的绘图区，可以看到实验曲线与理论曲线在x、y 轴上1∶1 叠合，可以通过滚动鼠标缩放，对细节进行仔细观察和精确比较.

图9 用GGB 处理实验数据得出的磁感应强度分布图

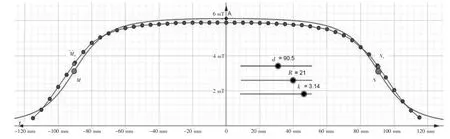
图10 磁感应强度理论分布图与测量分布图的叠加比较

对两条曲线上的一些特殊点取样，计算实验误差[9].用描点工具分别捕捉理论曲线上的三个特殊点，见图10，中点（x=0）为A（0,6.12），螺线管的两个端点（x=±L）为M（-90.5,3.12），N（90.5,3.12）；捕捉实验拟合曲线的中点Aa（0,5.88），实验拟合曲线螺线管的两个端点为Mm（-90.5,3.31），Nn（90.5,3.23），可得中点处的百分比误差为-3.92%，螺成管两端点处的误差为6.08%、5.52%.在中心的±85 mm 区间内两条曲线吻合度良好，曲线呈近乎水平状态，误差在4.0%之内，该区间可视为匀强磁场，在螺线管两端口附近存在边缘效应，磁感应强度的衰减较大，误差也较大.本次实验精度在螺线管80%以上的区间内误差小于4%，符合实验要求.

3 结语

将GeoGebra 软件应用于电磁学实验教学，在实验前对试验目标进行仿真，对学生理解电磁学物理现象和规律起到较好的辅助作用.对实验数据进行处理时，能方便地将实验结果与理论数值进行可视化的比较，极大减小实验数据的处理难度和人工误差，获得更准确的结果，节约了大量的计算时间.应用在电磁学实验教学中，不仅能提高教学质量，而且有利于提高学生的自主创新能力，激发学生的探索精神，在利用现代信息技术推动高校物理实验教学改革方面迈出积极的一步.