改进多尺度的Retinex红外图像增强

魏然然， 詹伟达， 朱德鹏， 田 永

(长春理工大学 电子信息工程学院，吉林 长春 130022)

1 引 言

近年来，红外成像系统由于具有良好的隐蔽性、较强的抗干扰能力以及可昼夜工作等特点而被广泛应用在军事和民用领域[1-3]。红外图像在获取时由于受到红外成像系统器件性能及波长等因素的影响，常常会表现出对比度较低、边缘细节不突出、视觉效果模糊等缺点[4]。这些缺点将严重影响到后续红外图像的观察、目标识别和目标探测等工作。因此，利用红外图像增强算法增强图像对比度、细节等已成为一种必不可少的图像处理操作。

常用的红外图像处理算法包括空域算法和频域算法。空域算法包括直方图均衡化算法和灰度变换等；频域算法包括傅里叶变换、小波变换、Culvelet变换和Contourlet变换等[5]。虽然这些算法都可以或多或少地对红外图像进行增强，但也存在一些缺点，如直方图均衡化算法和灰度变换在对红外图像增强的同时会放大噪声。Land等人首次提出Retinex理论，Retinex理论是一种非线性算法，其处理红外图像时可以在保留细节信息的同时降低图像噪声[6]。在Land的理论基础上，Jobson等人提出了一种单尺度的Retinex算法(SSR)，因为该方法只有一个参数，故其不能很好地兼顾动态范围压缩和色感一致性[7]。为了改进SSR算法，Rahman等人随后提出了多尺度Retinex算法(MSR)[8]。在该算法的基础上研究者们提出了一系列的改进算法。刘辉等人改进传统MSR算法，将算法中的指数用灰度线性拉伸代替，该算法虽然可以提高图像的对比度，改善图像的视觉效果，但其在操作过程中会扩大图像噪声，同时产生“光晕”现象[9]。张承泓等人使用自适应引导滤波器代替MSR算法中的高斯滤波器，该改进算法可以较好地去除图像中的“光晕”和噪声[10]。本文在前人研究的基础上，将改进引导滤波器模型使用到传统MSR算法中，以提出一种新的红外图像增强算法。

2 基础理论

2.1 多尺度Retinex理论

根据多尺度Retinex理论，一幅红外图像I(x,y)可以由入射分量L(x,y)和反射分量R(x,y)乘积得到，其数学表达式如下所示：

I(x,y)=L(x,y)R(x,y)

(1)

对式(1)两边同时取对数可得：

lnI(x,y)=ln(L(x,y)R(x,y))=
lnL(x,y)+lnR(x,y)

(2)

当L(x,y)=I(x,y)*G(x,y)时，反射分量可表示为：

lnR(x,y)=lnI(x,y)-
ln(I(x,y)*G(x,y))

(3)

式中，*表示卷积运算，G(x,y)为高斯滤波函数，其定义为：

(4)

式中，λ为满足时的归一化常数，δ为环绕参数。

式(3)又被称为单尺度Retinex算法(SSR)。由式(3)和式(4)可以看出，SSR只有单一的参数δ，该算法不能同时兼顾动态范围压缩和色感一致性。为了解决这一问题，研究者们提出了多尺度Retinex算法(MSR)，其主要思想是对每个尺度的SSR结果进行不同权重的加权平均，其数学表达式为：

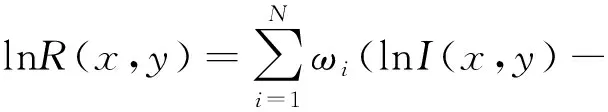
(5)

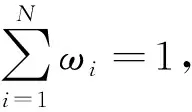
2.2 引导滤波

引导滤波器可以对图像进行线性滤波，其具有一定的边缘保持特性[11]。其数学模型如下：

qi=akIi+bk，∀i∈ωk

(6)

式中，qi为输出图像；Ii为引导图像；i、k表示像素索引；ωk为半径为r的局部方形窗口；ak和bk为ωk对应的线性系数。

对式(6)两边同时求梯度可得：

qi=aIi

(7)

式中，a为常数。

由式(7)可以看出qi与Ii具有相似的边缘梯度，而Ii的边缘平滑程度取决于ak。为了确定其值，需要使qi与pi的差异最小，则其代价函数如下所示[10]：

(8)

式中，ε为防止ak和bk过大的正则化因子。

利用线性回归法求解式(8)取最小值时，ak和bk的值为：

(9)

(10)

式中，|ω|为ωk中像素的数量；δk和μk为ωk中Ii的标准差和均值。

假设Ii=pi，则式(9)和式(10)可化为：

(11)

bk=μk(1-ak)

(12)

对式(6)、式(11)、式(12)进行分析可得，当ε=0时，ak=1，bk=0，故此时图像保持不变；当ε≫δk时，ak≈0，bk≈μk，qi≈μk，故当ωk处于低方差区域时，原始图像得到了平滑处理；当ε≪δk时，ak≈1，bk≈0，qi≈Ii，故当ωk处于高方差区域时，图像可以进行边缘保持操作。由以上操作可以看出,ε大小可以决定图像被平滑的程度，故ε又被称为平滑因子，对比高斯滤波的特点，引导滤波器也有决定其大小的尺度因子s。

3 本文算法

红外图像在获取时由于受到红外成像系统器件性能及波长等因素的影响，常常会表现出对比度较低、边缘细节不突出、视觉效果模糊等缺点。传统的MSR在解决这些问题时，会出现光晕现象和放大噪声等问题。为了解决这些问题，本文提出一种改进的MSR算法对红外图像进行图像增强。设待增强的红外图像为F(x,y)，增强后的红外图像为f(x,y)，改进引导滤波器输出的入射分量为L(x,y)，经过MSR计算得到的反射分量为R(x,y)，增强后的入射和反射分量分别为l(x,y)和r(x,y)，其具体算法实现框图如图1所示。

图1 本文算法实现框图Fig.1 Algorithm block diagram of this paper

3.1 入射分量估计

传统多尺度Retinex算法在图像边缘发生跃变处，不能精确估计光照分量即反射分量，进而产生“光晕”现象。为了解决这一问题，本文采用具有保边平滑的改进引导滤波器代替传统的高斯滤波器对光照层进行精确估计。

引导滤波器与高斯滤波器相比，虽然可以改善图像中的“光晕”现象，但其每个窗口对权重的取值均相同，没有考虑每个窗口的灰度差异。针对这一不足，对引导滤波器进行改进，具体方法为：首先计算窗内每个像素点的均值、标准差、平均梯度来作为该点特征，然后根据第k次的该点特征来求得权重值，最后对输出的引导图像加权平均。

图像像素点的均值、标准差、平均梯度定义如下：

(13)

(14)

(15)

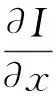
则权重值为：

(16)

(17)

式中，Uk(i,j)为质量测度，其由上述均值、标准差、平均梯度的一个或多个组成。对不同图像进行处理时，其侧重点不同，α，β，γ取值不同。α，β，γ其值可以为0或1。当α，β，γ中一个或两个为0时，说明图像的质量测度不采用此特性；当α，β，γ其中一个或全部为1时，表明此特性占有很大权重，图像的质量测度采取此特性。ε为一个很小的正数。

改进引导滤波输出图像为：

(18)

式中，Lk(i,j)为3次引导滤波对应的输出图像。

将原始图像F和引导图像I通过改进引导滤波器处理后得到输出图像即入射图像L为：

L=L(F,I)

(19)

式中，L(·)为改进引导滤波器操作。

为了验证本文改进引导滤波器的优越性，使用本文改进引导滤波器与传统高斯滤波器处理估计得到的入射分量图像，如图2所示(高斯滤波器参数选择：尺度因子取值为80；引导滤波参数选择：尺度因子为80，平滑因子取值为0.002)。根据图2可以看出，本文改进的引导滤波器可以更准确地对入射分量进行估计。

(a)原图(a)Origin image

(b) 传统高斯滤波器估计(b) Traditional Gaussian filter estimation

(c)改进的引导滤波器估计(c)Improved guide filter estimation图2 入射分量估计结果对比图Fig.2 Comparison of estimated results of incident components

3.2 入射分量自适应灰度拉伸

为了更好地提高入射分量的全局对比度，本文使用全局直方图均衡化来实现对入射分量的自适应灰度拉伸。对入射图像进行归一化处理后的分布函数为：

(20)

式中，Lk为第k级像素的像素值，nk为第k级像素的个数，n为像素总数，N为最大像素级。

若原入射分量的像素值为L，直方图均衡化后的像素值为l，则其灰度变换公式为：

(21)

式中，Li表示第i级像素的原像素值，p(Li)表示Li的概率。

根据以上理论，用MATLAB对图2(c)进行入射分量自适应灰度拉伸，结果如图3所示。

图3 图2(c)入射分量自适应灰度拉伸结果图Fig.3 Result of adaptive grayscale stretching of incident component of Fig.2(c)

3.3 反射分量非线性校正

反射分量中包含丰富的细节信息，但在其输出时，总体的亮度偏暗，对比度较低。为了调节反射分量的对比度，增强人眼视觉效果，大多数学者选择使用gamma曲线进行校正，但该校正方法容易产生过增强的现象。为了解决这一问题，本文使用以下非线性公式对其进行校正，具体公式如下：

(22)

(23)

式中，r为校正后的反射分量，RN为归一化后的反射分量，R为原始反射分量，Rmin和Rmax分别为R中像素最小值和最大值，t为调整参数。

在本次实验中，当t取值为0.1，gamma曲线参数取值为0.3。如图4所示，本文非线性校正曲线与gamma曲线校正相比，gamma曲线在低像素区域会出现拉伸过大的情况，进而导致细节信息出现过增强。本文校正曲线相对比较缓和，既可以很好地对图像中的细节信息进行图像增强，又可以避免图像失真。

图4 本文曲线与gamma曲线对比图Fig.4 Comparison between the curve in this paper and gamma curve

4 实验结果与分析

为了验证本文算法，选取4个红外图像场景进行对比实验(红外图像取自OTCBVS数据集)。首先，分别对这3个场景(如图5所示)使用直方图均衡化算法(HE)、单尺度Retinex算法(SSR)、多尺度Retinex算法(MSR)、基于引导滤波器的多尺度Retinex算法(未改进引导滤波+MSR)、文献[10]、本文算法来进行红外图像的增强；然后，通过对增强后的红外图像进行客观和主观评价来验证本文算法的优越性和可行性。本文所有算法均使用Matlab R2016b编译环境进行编程实现(DELL系列电脑，操作系统为Windows7，CPU为3.1 GHz，内存为4 GB)。本文算法的改进引导滤波器选用3个尺度，其相应窗口大小分别为20、70、115；SSR选择的参数σ=80；MSR选取3个尺度，每个尺度的高斯滤波参数为σ1=20，σ2=80，σ3=110，且本文中所有的多尺度MSR均采用相同的3个尺度。

图5 用于测试的4个不同场景的红外图像Fig.5 Infrared images of 4 different scenes for testing

4.1 主观评价

本文对选取的3幅场景进行不同算法比较，结果如图6～8所示。

由图6～8可以看出，HE算法对红外图像的对比度、亮度、边缘都有一定的增强。但图6、7中后面的背景细节信息严重丢失，图8中的船和人细节信息丢失。同时，图6～8中的噪声也很严重。SSR算法对红外图像中的亮度的到明显增强，但其增强图像的对比度较差，且有些地方产生了“光晕”现象，人眼视觉效果较差。图6中的左边飞机场窗口出现“光晕”。MSR算法增强的红外图像亮度有一定提高，“光晕”现象有所改善，但其对比度较低，部分背景信息丢失，红外图像整体视觉较差。图6和图7背景模糊，部分细节信息丢失。未改进的引导滤波器+MSR算法增强的红外图像边缘清晰度高，亮度有所增强，但其整体图像效果比较模糊，如图6和图8所示。文献[10]所得图像效果相对前面几种算法亮度有一定提升，有效改善了图像中的“光晕”现象，但其主要细节信息有所丢失。本文算法在有效去除“光晕”现象的同时，很好地提升了图像的对比度、细节和清晰度等，人眼整体视觉效果较好。

图6 场景1的各个算法比较实验结果Fig.6 Comparison experimental results of various algorithms in scene 1.

图7 场景2的各个算法比较实验结果Fig.7 Comparison experimental results of various algorithms in scene 2.

图8 场景3的各个算法比较实验结果Fig.8 Comparison experimental results of various algorithms in scene 3.

4.2 客观评价

为了进一步验证本文算法的有效性，本文选用图像标准差(SD)[12]、平均梯度(AVG)[13]、峰值信噪比(PSNR)[14]、信息熵(IE)[15]客观指标对增强的红外图像进行定量评价。

对以上3个场景分别进行客观指标评价，结果如表1～3所示。

表1 场景1不同算法所得红外增强图像的客观评价指标Tab.1 Objective evaluation indicators of infrared enhanced images obtained by different algorithms in scene 1

表2 场景2不同算法所得红外增强图像的客观评价指标Tab.2 Objective evaluation indicators of infrared enhanced images obtained by different algorithms in scene 2

表3 场景3不同算法所得红外增强图像的客观评价指标Tab.3 Objective evaluation indicators of infrared enhanced images obtained by different algorithms in scene 3

由表1～3可以看出：本文算法并不能同时兼顾SD、AVG、PSNR、IE，但本文算法相对其他算法相对占优。HE算法所得红外增强图像的标准差较高，但其得到的增强图像细节信息丢失，边缘模糊。本文算法处理得到的红外图像与SSR、MSR、未改进引导滤波器+MSR算法、文献[10]相比平均梯度(AVG)、信息熵(IE)较高，表明本文算法增强后的红外图像有更加丰富的信息量，图像更清晰。同时本文算法处理后的图像峰值信噪比(PSNR)较高，表明增强后的图像去除噪声更彻底，整体处理效果更好，对比度更强，人眼整体视觉效果更好。综上可以看出本文算法红外图像增强效果较好，且具有可行性和优化性。

5 结 论

本文提出一种基于改进多尺度Retinex的红外图像细节增强算法。该算法实验结果表明：利用改进引导滤波器代替高斯滤波器对入射分量进行精确估计，解决了原始算法放大噪声及产生“光晕”等问题；对反射分量进行校正时，使用一种平缓的非线性曲线代替常用的gamma曲线进行校正，解决了图像过增强问题，进一步提高了反射图像细节信息。同时，本文算法与HE、SSR、MSR、引导滤波+MSR算法相比，对红外图像的对比度、细节信息、人眼视觉效果都有很好的增强效果。