群钉连接装配式组合轨道梁受力特性研究

周 帅，聂建国，方 聪，罗桂军

（1.中国建筑集团有限公司，北京 100013；2.中国建筑第五工程局有限公司，湖南 长沙 410004；3.清华大学 土木水利学院，北京 100084）

发展轨道交通是解决城市交通拥堵、实现节能环保的主要方式之一。地铁建设投资大（＞6 亿元·km-1）、运输能力强（＞单向6 万人次·h-1）、运营成本高，主要用于人流集中的一线特大型城市。在广大的二三线中小城市，客流需求相对较小、地方财政相对较弱，以跨座式单轨为代表的中运量轨道交通可满足客运需求，且建设投资只有地铁的1/3～1/4，是合理的轨道交通制式选择[1-2]。

跨座式单轨交通是一种车辆骑跨在轨道梁上走行的交通制式，如图1所示。目前在全球范围内运营里程不足600 km，技术研发尚显不足。这类轨道交通制式的显著特点是“梁轨合一”，轨道梁既是承重结构，也是走行轨道，毫米级的线形精度是关键技术之一。混凝土轨道梁建造成本低，运营平稳性好，却面临着毫米级成桥线形精度的重大质量风险，已经通车的重庆轨道交通2，3号线和在建的广西柳州轨道2号线均有体现；全钢结构轨道梁线形精度易于保障、建设工期短，但经济成本高、运营噪声大、走行面耐候问题突出。因此，采用大跨径钢-混凝土组合轨道梁结构形式，扬长避短，是技术突破的方向之一。

图1 广西柳州跨座式单轨交通

采用剪力群钉的方式，可以实现组合轨道梁的下部钢箱和上部混凝土板均在工厂预制，现场装配化施工，缩短建设工期，降低预制梁厂费用，缓解混凝土板材料收缩徐变引起的质量风险。聂建国等建立和发展了钢-混凝土组合结构的等效刚度理论，对满铺剪力钉、开孔钢板、型钢等组合结构连接件做了大量的研究，并取得了很好的实践应用效果[3-4]。当前，关于群钉连接钢-混凝土组合结构的研究和应用则相对较少，叶梅新等对芜湖长江大桥群钉组合钢-混凝土主梁极限承载力开展了研究[5]；李成君对装配式钢-混凝土组合梁群钉构造及受力开展了相关研究[6]；项贻强等对复杂应力条件下快速施工钢-混组合梁群钉性能进行了分析[7]；邵旭东等对群钉钢-混凝土组合结构层间剪切性能进行了研究[8-9]。组合梁群钉连接不同于剪力钉均匀满铺，平截面假定适用性问题、等效刚度折减等问题需要进一步研究[10-11]。

本文基于实际的工程参数，按照1∶3的缩尺比设计制作群钉连接装配式组合轨道梁模型，全过程模拟构件预制、装配施工等主要过程，分别测试装配前、装配后的静动力特性，研究群钉连接装配式组合轨道梁的受力特性。

1 工程背景

庞巴迪车辆制式跨座式单轨双线车辆-轨道梁几何相对关系示意如图2所示。双线线间距4.6 m，简支50 m跨径双线钢-混凝土组合轨道梁梁高3.1 m，上部混凝土板厚度32 cm，宽度69 cm，下部钢箱高度278 cm，单片轨道梁宽高比达到1∶4.5，高跨比1∶16。

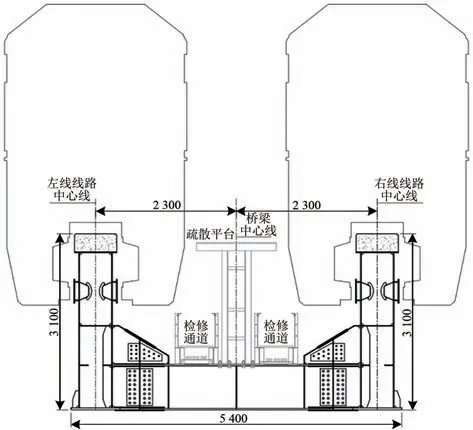
图2 车辆-轨道梁几何关系（单位：mm）

组合轨道梁上部混凝土板尺寸如图3所示，剪力预留槽尺寸为21 cm×90 cm，纵向中心距270 cm，横向错位布置，以降低“无钉区”长度。混凝土板在工厂预制、养生完成后运抵现场，与下部钢箱梁群钉对孔装配，后浇剪力预留槽高性能混凝土，实现钢箱-混凝土板组合。

图3 预制混凝土板群钉槽口平面布置图（单位：mm）

2 试验模型

依据钢-混凝土组合轨道梁原型尺寸，按照1∶3的几何缩尺比设计制作钢-混凝土组合轨道梁试验模型。

试验梁下部钢箱（简称钢梁）和上部混凝土板独立、分开预制，分别如图4和图5所示。剪力群钉在设计指定位置与钢箱焊接，混凝土板按设计位置及尺寸预留剪力预留槽。

图4 钢梁

图5 预制混凝土板

预制混凝土板养生完成后，运至钢梁位置吊装与剪力群钉对孔装配，如图6所示，后浇群钉预留槽高性能混凝土，形成钢-混凝土组合轨道梁（简称组合梁）。

图6 预制装配组合梁

集中荷载作用下简支梁的挠度计算式为

式中：S为组合梁跨中竖向挠度；P为简支组合梁跨中集中荷载；L为组合梁计算跨径；EI为组合梁截面刚度。

由式（1）得到组合梁等效竖弯刚度P/S为

钢梁、混凝土板连接界面无滑移和平截面假定是组合梁等效竖弯刚度理论建模的前提条件，传统均匀满铺剪力钉组合结构基本能满足基本假设，剪力钉集中非均匀布置条件下的组合梁群钉连接存在无钉区受力问题，传统理论适应性将通过有限元计算和试验实测进行验证。

3 组合梁动力特性

3.1 试验方案

钢梁、组合梁梁体放置于实验室平整地坪上，梁端底部通过临时滚轴支座支撑于地面，梁端可以有扭转自由度，约束3向平动自由度，模拟简支边界条件。测试所用传感器为拾振器，采样频率为1 000 Hz。

由于梁体较重，且加载位置空间与技术受限，动力测试采用人体跳跃方式对梁体进行激振，以获取结构上多点的自由衰减时程曲线，而后通过自由振动法，即采用FFT（快速傅里叶变换法）以及对数衰减率法，完成对该轨道梁的频率与阻尼比获取[12]。

3.2 实测结果与讨论

装配前钢梁和装配后组合梁实测时程曲线和频谱分别如图7—图10所示。由图7—图10可见：时程曲线呈现“拍现象”；FFT频谱分析得到钢梁、组合梁的1阶竖向弯曲固有频率分别为29.9 和32.2 Hz。

图7 装配前钢梁跨中加速度时程曲线

图8 装配前钢梁跨中频谱

图9 装配后组合梁跨中加速度时程曲线

图10 装配后组合梁跨中频谱

表1给出了3种方法得到的钢梁、组合梁竖向弯曲固有频率结果。其中，实测值为根据传感器实测数据分析得到的结果，计算值为根据有限元方法计算结果，理论值为界面无滑移钢-混凝土组合等效刚度理论结果[13-14]。

表1 竖弯固有频率结果对比

钢梁为规则的钢结构，实测值29.9 Hz 与计算值29.6 Hz 基本一致。混凝土板与钢梁组合以后，提高了整体竖弯刚度，也增加了等效质量，组合梁实测固有频率为32.2 Hz，略高于钢梁29.9 Hz。值得注意的是，组合梁实测值高于计算值，也高于理论值，原因可归结于激振方式和梁体刚度的非线性。由于组合梁刚度较大，人体跳跃对梁体的激振幅度相对较小，没有能够真实反映在大振幅作用下，群钉连接装配式组合梁等效刚度的折减效应，甚至由于预制混凝土板与钢梁的表面接触、摩擦等因素作用提高了梁体刚度的非线性，小幅荷载激励无法消除这一影响，使得实测结果偏大。

4 组合梁静力性能

4.1 试验方案

如图6所示，双线组合梁简支支撑于地面台座，通过试验机进行单侧加载，梁底设置接触式位移计与千分表，测试梁底的竖向位移值，沿组合梁长度方向梁端（A1和A5）、四分点（A2和A4）、跨中（A3），双线组合梁左右2幅共布设20个测量点。位移计量程有50和100 mm 2种，千分表量程有12 和25 mm 2种，灵敏度为0.002 mm。作用于梁体的加载点采用滚轴支撑的方式，减小与梁体表面的摩擦。

混凝土板与钢梁之间设置传感器，采用量程为12 mm的千分表，分别测量荷载作用下跨中、支座处、预制板湿接缝连接处、2侧剪力槽边缘处混凝土板与钢梁界面滑移值。沿组合梁截面高度设置应变片，测量截面高度应变数据，研究荷载作用下下部钢梁和上部混凝土板在同一截面的变形协调特征。

4.2 实测结果

不同荷载作用下，加载侧轨道梁的挠度曲线如图11所示。图中：A1—A5分别对应支点、四分点及跨中的平面位置。由图11可见：轨道梁的挠度随荷载的增加而增加，跨中挠度大于四分点挠度；梁底最大竖向挠度达到27.5 mm。

图11 不同荷载作用下梁体加载侧挠度曲线

单侧加载作用下，双线轨道梁挠度横向分布如图12所示，图中：A2，B2为加载侧梁体左四分点测点；C2，D2为非加载侧梁体左四分点测点。由图12可见，加载侧梁体挠度显著大于非加载侧，横向约束作用有限，以下将以加载侧梁体挠度为例进行等效刚度评价。

图12 不同荷载作用下跨中梁体双侧挠度横向分布

采用单侧加载的方式，集中荷载作用在组合梁跨中位置顶面，提取加载侧轨道梁梁底竖向位移作为组合梁最大挠度，荷载等级以100 kN为间隔，加载到800 kN，作用点混凝土局部压碎破坏，组合梁丧失协同变形能力。

3种方法得到的组合梁的荷载-最大竖向挠度曲线如图13所示。图中，计算值为根据组合梁模型实际尺寸进行有限元建模计算得到的结果，理论值是根据界面无滑移钢-混凝土组合等效刚度理论得到的结果。由图13可见：有限元和理论计算得到的荷载-最大竖向挠度曲线呈线性关系，而试验实测得到荷载-挠度曲线呈现非线性特征；同一等级荷载作用下，竖向挠度计算值总体大于理论值。

图13 组合梁荷载-最大竖弯挠度曲线

根据式（2）和图13荷载-竖向挠度关系，可以得到基于有限元计算、试验实测、理论计算3种不同方法的钢梁、组合梁等效竖弯刚度，结果见表3。由表3可知：钢梁材质单一，结构规则，所得等效竖弯刚度较为稳定，计算值和理论值一致，均为21.4 kN·mm-1，试验实测值为21.1 kN·mm-1，偏差在2%以内；由于考虑了混凝土板和钢梁界面的滑移，等效竖弯刚度有所折减，组合梁等效竖弯刚度计算值为31.5 kN·mm-1，小于不考虑界面滑移的理论值32.5 kN·mm-1。由图13可知，组合梁实测竖向挠度并非随着荷载的增加呈现线性关系，以500 kN荷载为界，小幅荷载作用下（＜500 kN），组合梁实测竖向挠度小于理论值，大幅荷载作用下（＞500 kN），组合梁实测竖向挠度大于理论值，因此，组合梁实测等效竖弯刚度并非恒定值，而表现出区间非线性效应，实测组合梁最小、最大等效竖弯刚度分别为29.1和35.9 kN·mm-1，分别对应理论值32.5 kN·mm-1的0.9和1.1倍。

表3 组合梁等效竖弯刚度对比

综上所述，在本研究工况中，以500 kN 荷载为界，小幅荷载作用下（＜500 kN），群钉连接装配式钢-混凝土组合梁实测等效竖弯刚度高于无滑移等效刚度理论值，提高幅度达到10%，因而可以合理解释本文3.2节组合梁固有频率研究中，组合梁等效质量一致的情况下，固有频率实测值32.2 Hz 高于理论值29.0 Hz的现象；大幅荷载作用下（＞500 kN），组合梁实测等效竖弯刚度低于理论值，并且随着荷载等级的提高，差距逐步增大，等效竖弯刚度进一步折减，折减幅度达到10%。因此，组合梁等效竖弯刚度表现出随着荷载增加而逐步降低的非线性特征。

相比于钢梁，由于预制混凝土板的叠合，组合梁截面惯性矩增大，等效竖弯刚度理论上提高幅度应为52%。由表3可知：在不同等级的荷载作用下，组合梁实测等效竖弯刚度为29.1～35.9 kN·mm-1，分别为钢梁实测等效竖弯刚度21.1 kN·mm-1的138%～170%，提高幅度为38%～70%，钢-混凝土组合梁叠合共同受力程度随着外加荷载量值的变化而表现出非线性效应。

在不同荷载等级作用下，组合梁跨中截面沿截面高度钢梁、混凝土板的应变如图14所示，试验梁整体梁高1 033 mm，上部预制混凝土板厚度107 mm，下部钢梁厚度926 mm，中性轴位置距离梁底583 mm。由图14可见：中性轴以上的钢梁和全部混凝土板均受压，中性轴以下均为钢梁，全部受拉，混凝土板最大压应力＜13.8 MPa，钢梁最大拉应力＜73.5 MPa，均处于弹性受力阶段。

图14 跨中截面变形协同曲线

由图14还可见：在100 kN荷载作用下，钢-混凝土组合梁界面以下（截面高度＜926 mm）钢梁的应变沿截面高度方向呈线性关系，所有测点均在同一直线上，组合界面以上（截面高度＞926 mm）混凝土板上缘应变（―162×10-6）显著大于等高度钢梁应变值（―64×10-6），比值为2.5；在200 kN 荷载作用下，钢梁和混凝土板的应变均大幅增加，而组合界面处混凝土板和钢梁同样存在应变突变的现象，混凝土板上缘应变（―367×10-6）显著大于等高度钢梁应变（―132×10-6），比值为2.8，上部混凝土板与下部钢梁存在变形不协调的受力特征。小幅荷载作用下（＜500 kN），混凝土板提前介入受力，在组合梁等效竖弯刚度中发挥了更多的作用，这在一定程度上可以解释上述刚度非线性的问题，由于混凝土板对组合截面的提前贡献，使得群钉连接装配式组合梁实测等效竖弯刚度大于理论值。

5 结 论

（1）群钉连接装配式钢-混凝土组合轨道梁呈现出随着作用荷载变化的非线性受力特征，荷载-挠度曲线存在1个反弯点，本试验组合梁刚度非线性反弯点对应跨中集中荷载500 kN，小幅荷载作用下（＜500 kN）等效竖弯刚度大，且大于理论值，随着作用荷载的增大，等效竖弯刚度逐步减小，经过反弯点后将折减到理论值以下，变化幅度在理论值的0.9～1.1倍。

（2）在钢梁和混凝土板共同受力的过程中，下部钢梁和上部混凝土板在同一截面的变形不协调，混凝土板的应变显著增大，偏离钢梁线性应变关系值，不满足平截面假定。

（3）在小幅设计荷载条件下，群钉连接装配式组合轨道梁等效刚度设计值可以按无滑移等效刚度理论取值，无须折减，组合梁固有频率也有提高；大幅设计荷载条件下应考虑群钉效应带来的刚度折减。