一类二阶微分方程的解及其稳定性
2021-04-10彭元媛范进军
彭元媛 范进军
(山东师范大学数学与统计学院,250358,济南)
1 引 言
有阻尼受迫振动、无阻尼受迫振动、有阻尼自由振动、理想状态下自由振动四种情况下的弹簧振子振动系统都可以用一类二阶微分方程进行刻画和描述[1-4].本文对这一类二阶微分方程的四种情况进行分析,考虑从定性角度应用奇点类型判断零解稳定性,从定量角度探讨解决周期解存在的条件.鉴于理论判断的抽象性,结合MATLAB强大的绘图功能[5-8],利用MATLAB绘制系统的轨线图,从直观上判断微分方程解的稳定性.
2 预备知识
为了对弹簧振子振动系统进行定性、定量分析并利用MATLAB软件进行相关问题的数值模拟,给出如下定义和引理.
定义1[1]对于平面自治系统
使X(x0,y0)=Y(x0,y2)=0的点(x0,y0),称为平面自治系统的奇点.
引理1[1]给定二维常系数线性自治系统

令p=-(a+d)=-π(A),q=ad-bc=det(A).当p>0,q>0时,若p2-4q>0,则奇点(0,0)是稳定的结点;若p2-4q<0,则奇点(0,0)是稳定的焦点;若p2-4q=0,则奇点(0,0)是稳定的临界结点或退化结点;当p=0,q>0时,奇点(0,0)是中心.
3 定性与定量分析
二阶微分方程(m≠0)
(1)
可以用于刻画弹簧振子振动系统,其中m,k分别表示弹簧的质量和弹簧的弹性系数,r为阻尼系数,lcosnt为所受强迫力.这一振动系统,共有如下四种情况:
i)当r≠0,l≠0时,方程(1)为有阻尼受迫振动方程;
ii)当r=0,l≠0时,方程(1)为无阻尼受迫振动方程;
iii)当r≠0,l=0时,方程(1)为有阻尼振动方程;
iv)当r=0,l=0时,方程(1)为自由振动方程.
下面主要研究二阶微分方程(1)的解及其解的稳定性.
3.1一般步骤
1)定性分析:由奇点理论分析对应齐次系统的奇点类型,进而判断系统的零解是否稳定.
2)定量分析:通过求出微分方程的通解,分析周期解存在的条件.
3)MATLAB数值模拟:选取适当的系统参数和初值,利用MATLAB绘制出系统特定解附近的轨线图及线素场,进而直观分析系统解的稳定性.
3.2定性分析通常利用李雅普诺夫第二方法来判断系统零解的稳定性,但构造李雅普诺夫函数比较困难.这里给出用奇点理论,通过判断奇点类型,进而判断系统零解稳定性的方法.
当l=0时,方程(1)为齐次线性方程
(2)

(3)
自治系统(3)对应的系数矩阵为

应用引理1知,若r2-4mk>0,则(0,0)为方程组(3)的稳定结点;若r2-4mk<0,则(0,0)为方程组(3)的稳定焦点;若r2-4mk=0,则(0,0)为方程组(3)的稳定的临界结点或退化结点;当r=0时,(0,0)为方程组(3)的中心.
因为方程组(3)的奇点(0,0)对应齐次方程(2)的零解,若方程组(3)的奇点是稳定的,则系统(2)的零解是稳定的.所以当l=0时,方程(1)的零解是稳定的.
3.3定量分析对于二阶微分方程(1),可以利用特征根法和常数变易法(或待定系数法),先求其通解,进而分析系统周期解存在的解析条件.
3.3.1 通 解 考虑系统(1)对应的齐次线性方程(2),其特征方程为
mλ2+rλ+k=0,
特征根为
下面,分三种情况讨论方程(1)的通解.
1)Δ=r2-4mk>0.此时λ1和λ2为实根,且λ2<λ1<0,方程(2)的一个基本解组为x1=eλ1t,x2=eλ2t.
易知方程(1)满足初始条件x(0)=0,x′(0)=0的解为
从而系统的通解为
其中C1,C2为任意常数.

易知方程(1)满足初始条件x(0)=0,x′(0)=0的解为
其中C1,C2为任意常数.

易知方程(1)满足初始条件x(0)=0,x′(0)=0的解为
其中C1,C2为任意常数.
综上,有阻尼受迫振动(r≠0,l≠0),即情况i)时方程(1)的通解为
其中C1,C2为任意常数.
同理可得:无阻尼受迫振动(r=0,l≠0),即情况ii)时方程(1)的通解为
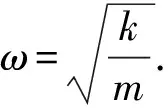
有阻尼振动(当r≠0,l=0),即情况iii)时方程(1)的通解为
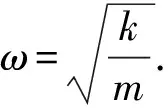
自由振动(r=0,l=0),即情况iv)时方程(1)的通解为
1998年之后,谷祺教授还带领一批博士生,深入研究财务危机企业投资行为分析与对策、EVA财务管理系统及其中国化、公司股价与剩余收益模型、公司治理与公司财务行为、新型两权分离与公司价值、会计信息复杂性与财务估价等财务领域的前沿问题,并在《会计研究》等期刊发表了一系列学术论文。这些论文不仅丰富了财务管理学术研究的视野,而且将委托代理理论、信息不对称理论、公司治理理论以及经济利润、估值模型等新的理论和概念引入财务管理领域,在研究视角、理论框架、研究方法等方面都做出了积极的尝试和探索。
x=C1cosωt+C2sinωt,即x=C1′cos(ωt+C2′),


1)Δ=r2-4mk>0.方程(2)的一个基本解组为x1=eλ1t,x2=eλ2t.这两个函数都不是周期函数,此时方程(2)和方程(1)都没有周期解.

其中C1,C2为任意常数.


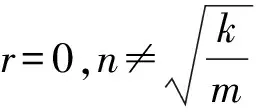
4 数值模拟
借助MATLAB绘制出平面自治系统在相平面上的轨线图及线素场,直观分析方程(1)解的稳定性.
4.1有阻尼受迫振动(r≠0,l≠0)的数值模拟对情况i)分以下几种情况进行数值模拟.
1)Δ=r2-4mk>0.取r=3,k=m=l=n=1,初始值(x,v)为(0,0),(0.05,0.05),(0.1,0.1),(0.2,0.2),(0.3,0.3),轨线图如图1所示,其中经过原点(0,0)的轨线用红色标出.
由图1可知,轨线由初始点起,快速靠近过(0,0)的解曲线,根据解稳定性定义,此时方程(1)满足初始条件x(0)=0,x′(0)=0的解是稳定的.

图1 Δ>0时的轨线图
2)Δ=r2-4mk<0.取k=10,r=m=l=n=1,初始值(x,v)为(0,0),(0.02,0.02),(0.05,0.05),(0.1,0.1),(0.2,0.2),轨线图如图2所示,其中经过原点(0,0)的轨线用红色标出.

图2 Δ<0时的轨线图
由图2可知,轨线由初始点起,呈螺旋状趋向于过(0,0)的解曲线,根据解稳定性定义,此时方程(1)满足初始条件x(0)=0,x′(0)=0的解是稳定的.
3)Δ=r2-4mk=0.取r=2,k=m=l=n=1,初始值(x,v)为(0,0),(0.05,0.05),(0.1,0.1),(0.2,0.2),(0.3,0.3),轨线图如图3所示,其中经过原点(0,0)的轨线用红色标出.同理,根据解稳定性定义,此时方程(1)满足初始条件x(0)=0,x′(0)=0的解是稳定的.

图3 Δ=0时的轨线图
4.2无阻尼受迫振动(r=0,l≠0)的数值模拟对情况ii)分以下几种情况进行数值模拟.

由图4可知,随着初始点与(0,0)的距离缩短,轨线向过(0,0)的解曲线靠近.根据解稳定性定义,此时方程(1)满足初始条件x(0)=0,x′(0)=0的解是稳定的.

图时的轨线图

由图5可知,随着初始点与(0,0)的距离缩短,轨线呈螺旋状向过(0,0)的解曲线靠近.根据解稳定性定义,此时方程(1)满足初始条件x(0)=0,x′(0)=0的解是稳定的.

图时的轨线图
4.3有阻尼振动(r≠0,l=0)的数值模拟对情况iii)分以下几种情况进行数值模拟.
1)Δ=r2-4mk>0.取m=1,k=1,r=3,初始值x,v分别取x=-0.4∶0.01∶0.4;v=-0.4∶0.01∶0.4, 线素场如图6所示、轨线图如图7所示.
根据图6和图7,并结合解稳定性定义,此时方程(1)的零解是稳定的.

图6 Δ>0时,(0,0)附近的线素场

图7 Δ>0时,(0,0)附近的轨线图
2)Δ=r2-4mk<0.取m=1,k=10,r=1,初始值x,v分别取x=-0.4∶0.01∶0.4;v=-0.4∶0.01∶0.4, 线素场如图8所示、轨线图如图9所示.
根据图8和图9以及解稳定性定义,此时方程(1)的零解是稳定的.

图8 Δ<0时,(0,0)附近的线素场
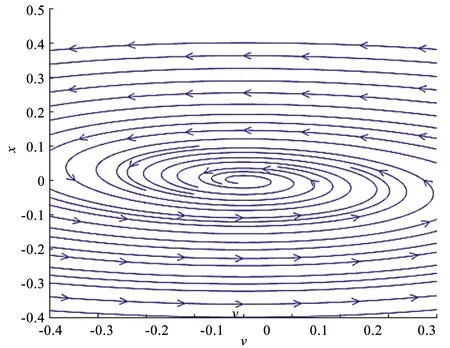
图9 Δ<0时,(0,0)附近的轨线图
3)Δ=r2-4mk=0.取m=1,k=1,r=2,初始值x,v分别取x=-0.4∶0.01∶0.4;v=-0.4∶0.01∶0.4, 线素场如图10所示、轨线图如图11所示.
基于图10和图11以及解稳定性定义,此时方程(1)的零解是稳定的.

图10 Δ=0时,(0,0)附近的线素场

图11 Δ=0时,(0,0)附近的轨线图
4.4自由振动(r=0,l=0)的数值模拟对情况iv)进行数值模拟.
取k=m=1,初始值x,v分别取x=-0.4∶0.01∶0.4;v=-0.4∶0.01∶0.4, 线素场如图12所示、轨线图如图13所示.
由图13可知,方程(1)的零解是稳定的.另外,线素场图12也可验证这一点.

图12 自由振动方程(0,0)附近的线素场

图13 自由振动方程(0,0)附近的轨线图
