二三混水平设计基于水平置换方法的最优折叠方案

2021-04-10李洪毅王治清欧祖军

兰州文理学院学报(自然科学版) 2021年2期

罗彪，李洪毅，王治清，欧祖军

(吉首大学数学与统计学院,湖南吉首 416000)

对两水平设计而言，折叠设计是通过将初始设计中一个或多个因子的符号反号而生成的跟随试验. 通过将折叠设计中的处理与初始设计中的处理结合获得的设计称为组合设计. 文献[1]最先在中心化L2-偏差下搜索最优折叠方案[2]. 对于多水平设计而言，通过反转初始设计中因子符号的折叠方法不再适用，因此在多水平折叠设计中可用有限的几何映射来定义折叠方案.文献[3]研究了正规的q水平部分因析设计的最优折叠方案.文献[4]通过对q水平因子使用modulo-q加法，提出了一种新的多水平因析设计的折叠结构，它适用于正规和非正规设计. 随后，他们将该方法推广到一般混水平的因析设计[5-6]. 针对三水平设计, 文献[7]通过对每个因子的水平进行水平置换，提出了一种新的折叠策略，进一步推广了文献[4]的结果并把文献[4]中的折叠策略作为特殊形式. 本文将文献[7]中提出的折叠策略推广到二三混水平设计，获得了组合设计的一些性质，并给出了可卷型L2-偏差一个新的下界.

1 预备知识

对于任意的设计d∈U(n;2s13s2), 下面基于表1中ψ0和ξ0的水平置换分别对两水平、三水平因子定义了新的折叠策略, 以及在新的折叠策略下的折叠设计与组合设计.

定义1对于任意的设计d=(d1,d2,…,ds)∈U(n;2s13s2), 其中dj表示设计d的第j列,j=1,…,s. 令

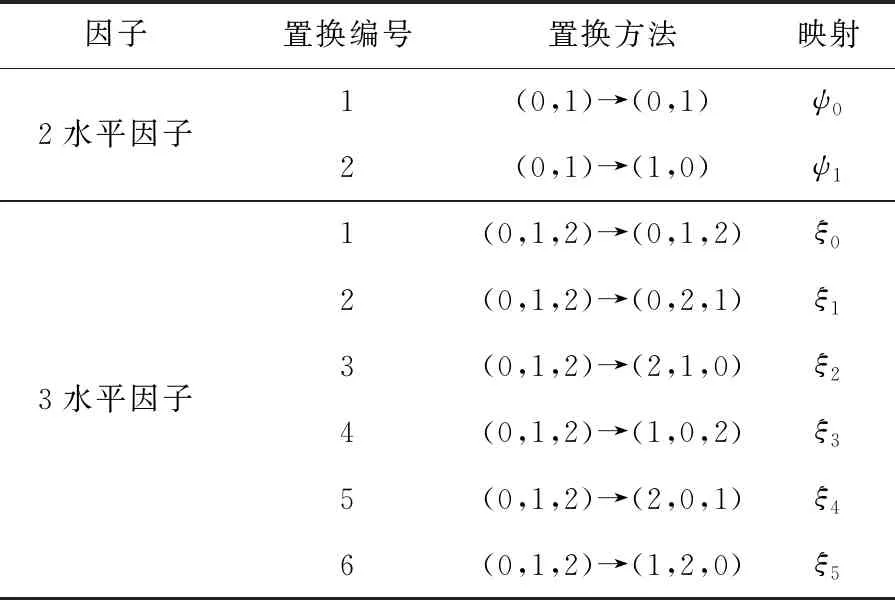
表1 ψ0和ξ0的水平置换表

Γ={γ=(γ1,γ2,…,γs)|γj1∈{ψ0,ψ1}),γj2∈{ξ0,ξ1,…,ξ6};j1=1,…,s1,j2=s1+1,…,s.}

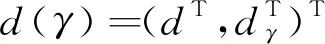
在本文中，以可卷型L2-偏差作为衡量设计均匀性的准则. 对任意的设计d=(dij)n×s∈U(n;2s13s2),dij可以映射到uij, 其中

则设计d的可卷型L2-偏差可表示为[2]

(1)

若折叠方案γ*使得

则将γ*称为设计d的最优折叠方案.

文献[5]利用modulo-q加法对二三混水平设计d进行折叠.在本文的折叠策略下, 文献[5]中的所有折叠方案为本文中的特殊情形，大幅地增加了折叠方案空间. 文献[5]给出了组合设计d(γ)的可卷型L2-偏差[WD(d(γ))]2的一个下界：

[WD(d(γ))]2≥LB1(γ),

其中,

其中:t1表示折叠方案γ中γi取ψ1的个数;t2表示折叠方案γ中γj取ξ4和ξ5的总个数，i=1,…,s1，j=s1+1,…,s.

2 主要结果

对给定初始设计d∈U(n;2s13s2)，本节讨论了定义1中折叠结构的性质, 获得了组合设计d(γ)的可卷型L2-偏差[WD(d(γ))]2的一个新下界, 为在Γ中搜索设计d的最优折叠方案提供了基准.

(2)

其中,

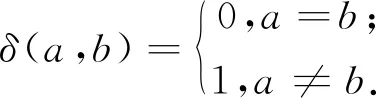
所以, 式(1)中的[WD(d)]2可进行如下转化

(3)

其中:hil为设计d中第i行与第l行二水平因子列的重合数;λil为设计d中第i行与第l行三水平因子列的重合数.

对于任意的γ=(γ1,γ2,…,γs)∈Γ, 令hil(γ)为原始设计d中第i行与折叠设计dγ中第l行之间二水平因子列的重合数,λil(γ)为原始设计d中第i行与折叠设计dγ中第l行之间三水平因子列的重合数,i,l=1,…,n, 则组合设计d(γ)的可卷型L2-偏差[WD(d(γ))]2转化为重合数的函数形式, 见引理1.

引理1设d∈U(n;2s13s2), 对任意的折叠方案γ=(γ1,γ2,…,γs)∈Γ, 有

(4)

其中hil与λil如式(3)所定义.

证明由d(γ)的定义, 根据式(1)，有

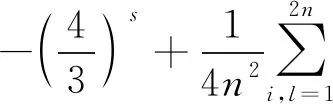
证明完成.

设计d=(d1,d2,…,ds)∈U(n;2s13s2),dγ=(d1(γ1),d2(γ2),…,ds(γs))为设计d在折叠方案γ=(γ1,γ2,…,γs)∈Γ的折叠设计. 令g=0,1,k=0,1,…,5, 定义

Ag={i1|γi1=ψg,i1=1,…,s1},Bk={i2|γi2=ξk,i2=s1+1,…,s},dg={di1|i1∈Ag,i1=1,…,s1},dk={di2|i2∈Bk,i2=s1+1,…,s},dg(γ)={di1(γ)|i1∈Ag,i1=1,…,s1},dk(γ)={di2(γ)|i2∈Bk,i2=s1+1,…,s},fg=#{Ag},tk=#{Bk}.

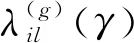
为了得到组合设计d(γ)的可卷型L2-偏差[WD(d(γ))]2的下界, 下面介绍两个引理.

引理2设d∈U(n;2s13s2), 对任意的γ=(γ1,γ2,…,γs)∈Γ, 则有

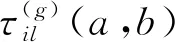
当g=0时, 对i,l=1,2,…,n,

同样的方法可得到g=1时的情形, 对于i,l=1,2,…,n, 可得

当i=l时,

同理, 当1≤i≠l≤n时,

证明完成.

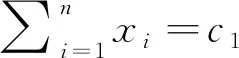
(5)

其中k是使得z(k)≤c/n≤z(k+1)成立的最大整数,p和q是使p+q=n和pz(k)+qz(k+1)=c成立的非负实数.

为了方便,给出[WD(d(γ))]2的新下界, 令

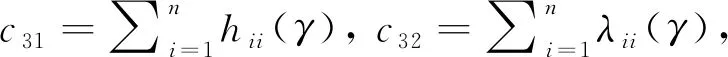
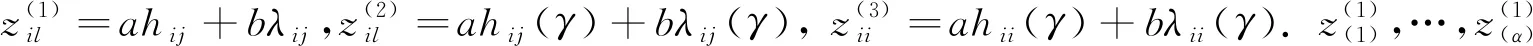
定理1设d∈U(n;2s13s2)，对任意的γ=(γ1,γ2,…,γs)∈Γ，有

[WD(d(γ))]2≥LB2(γ),

其中,

证明根据引理1和引理3，[WD(d(γ))]2可表示为:

证明完成.

3 数值例子

在本节中，将本文与文献[5]所得到的组合设计以及下界进行了数值比较. 对于任意的设计d∈U(n;2s13s2), 记θ*表示初始设计d为文献[5]中的折叠策略得到的最优折叠方案,LB1(θ*)表示[WD(d(θ*))]2的下界, 令γ*表示初始设计d为本文中的折叠策略得到的最优折叠方案,LB2(γ*)表示[WD(d(γ*))]2的下界.

例1考虑如下初始设计d1∈U(n;2332), 其中n=6,s1=3,s2=2，

根据文献[5]中的折叠策略和下界, 得到的最优折叠方案为:

θ*=(ψ1,ψ0,ψ0,ξ0,ξ5),

[WD(d1(θ*))]2=0.5557,

LB1(θ*)=0.5195,LB2(θ*)=0.5309.

运用本文的折叠方法和新的下界，则可得到设计d1的最优折叠方案

γ*=(ψ0,ψ1,ψ1,ξ4,ξ0),

[WD(d1(γ*))]2=0.5491,

LB2(γ*)=0.5058.

例2考虑如下初始设计d2∈U(n;2333), 其中n=6,s1=3,s2=3.

根据文献[5]中的折叠策略和下界, 得到的最优折叠方案为:

θ*=(ψ1,ψ1,ψ1,ξ5,ξ0,ξ0),