三角代数上Lie积为平方零元的非线性双可导映射
2021-04-10费秀海张海芳
费秀海, 戴 磊, 张海芳*
(1.滇西科技师范学院数理学院, 云南 临沧 677099; 2.渭南师范学院数学与信息科学学院, 陕西 渭南 714099)
1 预备知识
设A是交换幺环R上的一个代数,Z(A)表示A的中心,δ:A→A是A上的一个可加映射,Ω={x∈A:x2=0}.若对任意的x,y∈A,有δ(xy)=δ(x)y+xδ(y),则称δ是一个导子.若存在a∈A,使得对任意的x∈A, 有δ(x)=[a,x] ,则称δ是一个内导子.设φ:A×A→A是A上的一个双可加映射且φ在每一个变量上都是导子,则称φ是一个双导子.进一步,若φ没有双可加假设且对任意的x,y,z∈A,当[x,y],[y,z]∈Ω时φ分别满足:
φ(xy,z)=φ(x,z)y+xφ(y,z)
(1)
和
φ(x,yz)=φ(x,y)z+yφ(x,z),
(2)
则称φ是一个Lie积为平方零元的非线性双可导映射.设λ∈Z(A),若对任意的x,y∈A,有φ(x,y)=λ[x,y],则称φ是一个内双导子.设a∈A,使得对任意的x,y∈A,有[a,[x,y]]=0,则称φ(x,y)=[x,[a,y]]是一个超双导子.显然,内双导子和超双导子都是双导子.
设A和B是含有单位元的交换环R上的代数,M是含有单位元的忠实(A,B)-双边模,即M既是忠实左A模又是忠实右B模,则称R-代数
U=Tri(A,M,B)=

在矩阵通常的加法与乘法运算下是一个三角代数.
用Z(U)表示U的中心,由文献[1]有

在U上定义两个自然投影πA:U→A和πB:U→B如下:
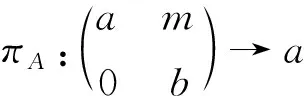
则πA(Z(U))⊆Z(A)和πB(Z(U))⊆Z(B),且存在唯一的代数同构σ:πA(Z(U))→πB(Z(U))使得对任意的m∈M,有am=mσ(a).
设1A和1B分别是代数A和B中的单位元,1是三角代数U中的单位元.用e1和e2分别表示:
则由于e1Ue1,e1Ue2和e2Ue2是U的子代数且分别同构于A,M和B,从而三角代数U在同构意义下可以被分解成:
U=e1Ue1+e1Ue2+e2Ue2=A+M+B,
进而对任意的x∈U,可以将x分解成x=a+m+b(其中a∈A,m∈M和b∈B).
近年来,关于三角代数上各种映射的研究引起了许多学者的关注.如:三角代数上的交换映射[1-3],三角代数上的Jordan导子和导子[4-7],三角代数上的Lie导子[8-13].特别地,在双可加或双线性假设下,文献[14]刻画了套代数上的广义双导子,文献[15]刻画了上三角矩阵代数上的双导子,文献[16]在一定条件限制下对三角代数上的双导子进行了刻画.本文主要考虑了三角代数上Lie积为平方零元的非线性双可导映射的双可加性,证明了三角代数上Lie积为平方零元的非线性双可导映射就是双导子,进而由文献 [16] 得到在一定条件限制下三角代数上Lie积为平方零元的非线性双可导映射都是内双导子.
2 结果与证明
定理1设U是一个三角代数,φ:U×U→U是U上的一个Lie积为平方零元的非线性双可导映射,则φ是U上的一个双导子.
为证定理 1,需要以下几个引理,在证明过程中,总假设U是一个三角代数, Ω={u∈U:u2=0},φ:U×U→U是U上的一个Lie积为平方零元的非线性双可导映射.
引理1若φ:U×U→U是U上的一个Lie积为平方零元的非线性双可导映射,则
i) 对任意的u∈U,有φ(u,0)=φ(0,u)=0;
ii)φ(e1,e1)=-φ(e1,e2)=-φ(e2,e1)=φ(e2,e2)∈M.
证明i)对任意的u∈U, 由于[u,0]=0∈Ω,从而可在(2)式中令y=z=0,故可得φ(u,0)=φ(u,0)0+0φ(u,0)=0,所以φ(u,0)=0.类似地,可证明φ(0,u)=0.
ii)由于[e1,e1]=[e2,e2]=0∈Ω,从而一方面,在(1)式中分别令x=y=z=e1和x=y=z=e2,得
φ(e1,e1)=φ(e1e1,e1)=φ(e1,e1)e1+e1φ(e1,e1)
和
φ(e2,e2)=φ(e2e2,e2)=φ(e2,e2)e2+e2φ(e2,e2),
从而有
φ(e1,e1)=e1φ(e1,e1)e2
和
φ(e2,e2)=e1φ(e2,e2)e2.
(3)
另一方面,在(1)式中分别令x=y=e1,z=e2和x=y=e2,z=e1,可得
φ(e1,e2)=φ(e1,e2)e1+e1φ(e1,e2)
和
φ(e2,e1)=φ(e2,e1)e2+e2φ(e2,e1),
从而有
φ(e1,e2)=e1φ(e1,e2)e2
和
φ(e2,e1)=e1φ(e2,e1)e2.
(4)
从而由引理1 i),(3)式和(4)式,可得
0=φ(e1,0)=φ(e1,e1e2)=
φ(e1,e1)e2+e1φ(e1,e2)=
φ(e1,e1)+φ(e1,e2)
(5)
和
0=φ(0,e1)=φ(e1e2,e1)=
φ(e1,e1)e2+e1φ(e2,e1)=
φ(e1,e1)+φ(e2,e1),
(6)
及
0=φ(0,e2)=φ(e1e2,e2)=
φ(e1,e2)e2+e1φ(e2,e2)=
φ(e1,e2)+φ(e2,e2).
(7)
从而由式(5) ~(7),有
φ(e1,e1)=-φ(e1,e2)=
-φ(e2,e1)=φ(e2,e2)∈M.
引理2若φ:U×U→U是U上的一个Lie积为平方零元的非线性双可导映射,则
i) 对任意的u∈U,φ(e1,u)=-φ(e2,u)∈M和φ(u,e1)=-φ(u,e2)∈M;
ii)φ(A,U),φ(U,A)⊆A+M;
iii)φ(U,B),φ(B,U)⊆M+B;
iv)φ(U,A+M),φ(A+M,U)⊆A+M;
v)φ(U,M+B),φ(M+B,U)⊆M+B;
vi)φ(U,M)⊆M,φ(M,U)⊆M.
证明i)对任意的u∈U,由于[e1,e1]=[e2,e2]=0∈Ω,从而可在(1)式中分别令x=y=e1,z=u和x=y=e2,z=u,可得
φ(e1,u)=φ(e1,u)e1+e1φ(e1,u)
和
φ(e2,u)=φ(e2,u)e2+e2φ(e2,u),
从而有
e1φ(e1,u)e1=e2φ(e1,u)e2=0
和
e1φ(e2,u)e1=e2φ(e2,u)e2=0,
所以有
φ(e1,u)=e1φ(e1,u)e2
和
φ(e2,u)=e1φ(e2,u)e2.
(8)
下证φ(e1,u)=-φ(e2,u).事实上,由于[e1,e2]=0∈Ω,从而可在(1)式中令x=e1,y=e2,z=u,从而有0=φ(0,u)=φ(e1e2,u)=φ(e1,u)e2+e1φ(e2,u),进而由(8)式得φ(e1,u)=-φ(e2,u).类似地,可证明φ(u,e1)=-φ(u,e2)∈M.
ii)对任意的a∈A和u∈U,由于[a,e1]∈Ω,从而可在 (1) 式中令x=a,y=e1,z=u,从而有
φ(a,u)=φ(ae1,u)=φ(a,u)e1+aφ(e1,u).
(9)
从而e2φ(a,u)e2=0,可得φ(A,U)⊆A+M.同理可证φ(U,A)⊆A+M.
iii)类似ii),可证明 iii).
iv)对任意的u∈U,a∈A和m∈M,由于[e1,a+m]=m∈Ω,从而可在(2)式中令x=u,y=e1,z=a+m,从而由引理2 i)有
φ(u,a+m)=φ(u,e1(a+m))=
e1φ(u,a+m),
从而e2φ(u,a+m)e2=0,故可得φ(U,A+M)⊆A+M,同理可得φ(A+M,U)⊆A+M.
v)类似iv),可证明v)成立.
vi)对任意的u∈U和m∈M,由于[e1,m]=[m,e2]=m∈Ω, 从而可在(1)式中分别令x=u,y=e1,z=m和x=u,y=m,z=e2,进而由引理2 i)有φ(u,m)=φ(u,e1m)=e1φ(u,m)和φ(u,m)=φ(u,me2)=φ(u,m)e2.由此可得e1φ(u,m)e1=e2φ(u,m)e2=0,所以φ(U,M)⊆M.类似地,可证明φ(M,U)⊆M.
引理 3若φ:U×U→U是U上的一个Lie积为平方零元的非线性双可导映射,则
i)对任意的a∈A,m∈M和u∈U,有
φ(a+m,u)=φ(a,u)+φ(m,u)
和
φ(u,a+m)=φ(u,a)+φ(u,m);
ii)对任意的m∈M,b∈B和u∈U,有
φ(m+b,u)=φ(m,u)+φ(b,u)
和
φ(u,m+b)=φ(u,m)+φ(u,b);
iii)对任意的m1,m2∈M和u∈U,有
φ(m1+m2,u)=φ(m1,u)+φ(m2,u)
和
φ(u,m1+m2)=φ(u,m1)+φ(u,m2);
iv)对任意的a1,a2∈A和u∈U,有
φ(a1+a2,u)=φ(a1,u)+φ(a2,u)
和
φ(u,a1+a2)=φ(u,a1)+φ(u,a2);
v)对任意的b1,b2∈B和u∈U,有
φ(b1+b2,u)=φ(b1,u)+φ(b2,u)
和
φ(u,b1+b2)=φ(u,b1)+φ(u,b2);
vi)对任意的a∈A,m∈M,b∈B和u∈U,有
φ(a+m+b,u)=φ(a,u)+φ(m,u)+φ(b,u)
和
φ(u,a+m+b)=φ(u,a)+φ(u,m)+φ(u,b).
证明i)对任意的a∈A,m∈M和u∈U,由于[a+m,e1]=[a+m,e2]=m∈Ω,从而可在 (1) 式中分别令x=a+m,y=e1,z=u和x=a+m,y=e2,z=u,从而由引理2 i)分别可得
φ(a,u)=φ(a+m,u)e1+aφ(e1,u)
和
φ(m,u)=φ(a+m,u)e2-aφ(e1,u).
把上述两式相加,可得φ(a+m,u)=φ(a,u)+φ(m,u).
ii)类似地,可证明φ(u,a+m)=φ(u,a)+φ(u,m)和ii)成立.
iii)对任意的m1,m2∈M和u∈U,由于[e1+m1,m2+e2]=m1+m2∈Ω,从而在(1)式中令x=e1+m1,y=m2+e2,z=u,故由引理2和引理3 的i)、ii),有
φ(m1+m2,u)=φ((e1+m1)(m2+e2),u)=
φ(e1+m1,u)(m2+e2)+(e1+m1)φ(m2+e2,u)=
(φ(e1,u)+φ(m1,u))(m2+e2)+
(e1+m1)(φ(m2,u)+φ(e2,u))=
φ(e1,u)+φ(m1,u)+φ(m2,u)+φ(e2,u)=
φ(e1,u)+φ(e2,u)+φ(m1,u)+φ(m2,u)=
φ(m1,u)+φ(m2,u).
类似地,可证明
φ(u,m1+m2)=φ(u,m1)+φ(u,m2).
iv)对任意的a1,a2∈A和u∈U,由引理2 i)、ii)和(9)式,可得e1φ(a1,u)e2=a1φ(e1,u)和e1φ(a2,u)e2=a2φ(e1,u) , 从而
φ(a1+a2,u)=φ((a1+a2)e1,u)=
φ(a1+a2,u)e1+(a1+a2)φ(e1,u)=
e1φ(a1+a2,u)e1+a1φ(e1,u)+
a2φ(e1,u)=e1φ(a1+a2,u)e1+
e1φ(a1,u)e2+e1φ(a2,u)e2.
(10)
下证
e1φ(a1+a2,u)e1=e1φ(a1,u)e1+e1φ(a2,u)e1.
对任意的m∈M,由[a1+a2,m]=a1m+a2m∈Ω,从而可在(1)式中令x=a1+a2,y=m,z=u,一方面,由引理2 vi),有
φ(a1m+a2m,u)=φ(a1+a2,u)m+
(a1+a2)φ(m,u).
(11)
另一方面,由引理2 iii)有
φ(a1m+a2m,u)=φ(a1m,u)+φ(a2m,u),
又因为[a1,m],[a2,m]∈Ω,从而由(1)式得
φ(a1m+a2m,u)=φ(a1,u)m+a1φ(m,u)+
φ(a2,u)m+a2φ(m,u).
(12)
比较(11)式和(12)式得
(φ(a1+a2,u)-φ(a1,u)-φ(a2,u))m=0,
进而由M的忠实性,有
e1φ(a1+a2,u)e1=
e1φ(a1,u)e1+e1φ(a2,u)e1.
(13)
因此,由(10)式和(13)式及引理2 ii),得φ(a1+a2,u)=φ(a1,u)+φ(a2,u).
v)类似地,可证明φ(u,a1+a2)=φ(u,a1)+φ(u,a2)和v)成立.
vi)对任意的a∈A,m∈M,b∈B和u∈U,由于[a+m+b,e1]=m∈Ω和[a+m+b,e2]=m∈Ω,从而在(1)式中分别令x=a+m+b,y=e1,z=u和x=a+m+b,y=e2,z=u,则由引理2 i)、ii)和(9)式,有
φ(a,u)=φ((a+m+b)e1,u)=
φ(a+m+b,u)e1+aφ(e1,u)=
φ(a+m+b,u)e1+e1φ(a,u)e2
和
φ(m+b,u)=φ((a+m+b)e2,u)=
φ(a+m+b,u)e2+aφ(e2,u)=
φ(a+m+b,u)e2-e1φ(a,u)e2.
把上述两式相加,并由引理3 ii),有
φ(a+m+b,u)=φ(a,u)+φ(m,u)+φ(b,u).
类似地,可以证明
φ(u,a+m+b)=φ(u,a)+φ(u,m)+φ(u,b).
定理1的证明对任意的x,y,z∈U,设
x=a1+m1+b1,y=a2+m2+b2,
由引理3有
φ(x+y,z)=
φ((a1+m1+b1)+(a2+m2+b2),z)=
φ((a1+a2)+(m1+m2)+(b1+b2),z)=
φ(a1+a2,z)+φ(m1+m2,z)+φ(b1+b2,z)=
φ(a1,z)+φ(a2,z)+φ(m1,z)+
φ(m2,z)+φ(b1,z)+φ(b2,z)=
φ(a1+m1+b1,z)+φ(a2+m2+b2,z)=
φ(x,z)+φ(y,z).
类似地,可以证明φ(x,y+z)=φ(x,y)+φ(x,z),从而φ是U上的一个双可加映射,所以φ是三角代数U上的一个双导子.
由定理1及文献 [16] 中定理 4.11,可以得到以下结论.
定理2设U是一个三角代数,φ:U×U→U是U上的一个Lie积为平方零元的非线性双可导映射.若满足:
i)πA(Z(U))=Z(A)和πB(Z(U))=Z(B);
ii) 代数A和B至少有一个非交换;
iii) 设a≠0∈A和b∈Z(A),若ba=0,则b=0;
iv) 代数A上的导子都是内导子;
v)φ(e1,e1)=0.
则存在λ∈Z(U), 使得任意的x,y∈U,有
φ(x,y)=λ[x,y].
由于上三角分块矩阵代数和套代数是两类特殊的三角代数,因此定理1和定理2的结论在这两类代数上仍然成立.
