锂离子在石墨、MoS2 及其复合材料中扩散过程的分子模拟及量子力学研究

张少阳， 刘 宇， 刘洪来

（华东理工大学化学工程联合国家重点实验室，化工学院，上海 200237）

锂离子电池（LIBs）是一种高效的能量存储装置，具有能量密度高、比体积小、寿命长、成本低等优点[1-4]。在LIBs 中，石墨具有优异的物理化学性能和廉价易得的特性，是目前应用最为广泛的电极材料。MoS2具有与石墨相似的二维结构，且有较高的理论容量（670 mA·h/g）。MoS2与石墨的复合材料（G/MoS2）由于其性能一般优于单纯的石墨和MoS2[5-7]，因而受到了学术界的广泛关注。例如，Tiwari 等[8]合成了三维的G/MoS2/G 复合材料，发现其比容量（1260mA·h/g）和循环稳定性（循环100 次后，比容量保持在810 mA·h/g）都远高于MoS2。Wang 等[9]使用超声技术，制备了G/MoS2异质结构复合材料，证明了材料中C−S 键的存在对锂离子的运输非常有利。

从原理上说，电池的比容量、功率等均与锂离子的传递扩散性能密切相关，尤其是电池的充放电速率直接由该传递扩散过程决定，因此，研究锂离子在电极材料中的传递扩散过程具有重要的实际意义[10-15]。目前，锂离子的扩散过程主要通过锂离子的自扩散系数（D）进行描述。一般情况下，扩散系数可分为两种：传递扩散系数和自扩散系数。前者由宏观Fick定律定义，从非平衡态的角度描述物质的宏观传递过程；后者由Einstein 扩散方程定义，描述平衡系统中物质的流动性。在计算过程中，两者通常在数值上相差较大，变化趋势也不尽相同。对于锂离子在电极材料中的传递，由于充放电过程中锂离子处于典型的非平衡态，因而传递扩散系数能更好地反映体系的传递特征。针对锂离子的扩散，目前已有许多的实验研究，例如，González 等[16]通过离子插层对MoS2进行化学改性，测定和分析了改性前锂离子的扩散系数（10−13～10−14cm2/s）和改性后锂离子的扩散系数（10−10～10−12cm2/s），发现改性后MoS2的扩散输运性能明显提高。Rui 等[17]采用循环伏安法（CV）、电化学阻抗谱（EIS）和恒电流间歇滴定法（GITT），系统地测定了锂离子在Li3V2(PO4)3中的化学扩散系数，探究了不同电压下锂离子扩散系数的变化。为了排除外界条件对实验的干扰，使数据更加准确，近年来也常采用计算机模拟来验证确定扩散系数。例如，文献[18-19]运用第一性原理研究锂离子在石墨烯上的吸附与扩散性质，证明点缺陷可以增强石墨烯对锂离子的吸附，且锂离子主要在平行于石墨烯的方向扩散。林传金等[20]运用密度泛函理论（DFT）计算了锂离子在Li2FeO2材料中的迁移势垒及扩散系数，确定了锂离子的最佳迁移路径。文献[21-22]运用从头算分子动力学（AIMD）模拟和热力学积分方法预测锂离子从LiC6阳极到电解质溶液中的自由能势垒。在研究过程中他们发现电极/电解液界面上的表面电荷是锂离子传输的关键。

此外，锂离子的传递扩散受晶胞参数[23-25]、边缘结构[21,26-27]、复合构型[9,28]等诸多因素的影响。如Qiu 等[29]通过离子掺杂改变了材料的晶胞参数，增强了材料结构的稳定性及电化学性能，揭示了晶胞参数对电池性能的影响。在模拟计算中，目前关于这些因素的理论研究体系大多数基于平衡态考虑，而忽略了非平衡态下的性质，并不能代表全部的动力学特征。因此，在本文中，我们将采用非平衡态分子动力学（NEMD）模拟并结合平衡态和量子力学研究，系统探究锂离子在石墨、MoS2及其复合材料G/MoS2中的扩散性质。

1 理论和建模

采用分子动力学（MD）方法模拟锂离子电池的充电过程。如图1 所示，模拟盒子（20.6 nm×2.46 nm×2.04 nm）沿着X 轴分为电极和真空两个区域。其中电极由一组平行于XOY 面的石墨或MoS2构建，初始层间距分别为0.34 nm 和0.61 nm。

图1体系在分子动力学模拟中的初始态Fig.1A initial state of the system in the MD simulation

分子动力学模拟时采用Material Studio 材料计算软件中的Forcite 模块，并选用正则系综（NVT）。在初始状态，将150 个锂离子放置在真空区的右侧，距离电极8 nm（图1）。首先，为了仿真充电过程中的电场，在电极中的碳原子或钼和硫原子上附加额外的电荷。其次，为了保持整个模拟盒子电荷中立，电极上的净电荷数应等于系统中锂离子的总电荷数。在这种情况下，系统的静电荷密度为260 mA·h/g，产生的初始电场为1.7×109V/m。在分子动力学模拟中，假定电极是刚性的，Van de Waals 相互作用模型采用通用力场（UFF），并利用Quadrature Equalizer（QEq）方法对电极原子上的电荷进行参数化。Van de Waals势长程作用的截断半径r 为1 nm，静电相互作用由Ewald 加和法计算，其精度为0.42 J/mol。系统的温度由Nose 方法控制，设定为298 K。平衡态分子动力学（EMD）模拟的时间长度和时间步长分别为2 ns 和1 fs，NEMD 模拟的时间长度和时间步长分别为100 ps 和1 fs。其中，EMD 通过Einstein 方程来计算自扩散系数（式（1）），式中t 为平衡扩散时间，r(t)为t 时刻对应的坐标，r0为初始态锂离子的坐标。对于每个系统，最后的结果均取20个独立模拟数据的平均值。

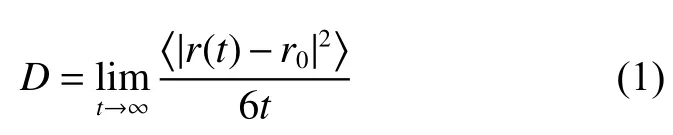
同时，利用量子密度泛函理论（QDFT）计算石墨、MoS2与锂离子之间的吸附能E。

式中： Esub代表石墨或MoS2的能量， ELi+代表锂离子的能量， Esub+Li+代表石墨或MoS2与锂离子的总能量。量子力学模拟采用Material Studio 软件中的Castep 模块。交换关联函数采用广义梯度近似（Generalized Gradient Approximation, GGA）和PBE（Perdew-Burke-Ernzerhof）方法。体系算法采用线性搜索拟牛顿法（BFGS），DFT 赝势法采用Ultrasoft，并选用自动校正模式。初始结构由Material Studio软件建立，其他原子的位置通过能量最小原理来进行优化。当单位原子的能量、最大力、最大压力和最大位移的变化分别小于1.0×10−5eV、0.3 eV/ nm、0.05 GPa 和1.0×10−4nm 时，认为系统达到平衡。在模拟中，石墨的模拟盒子规格为a=b=0.74 nm，c=0.78 nm，α=β=90°，γ=120°；MoS2的模拟盒子规格为a=b=0.63 nm，c=1.22 nm，α=β=90°，γ=120°。

为了定量检测锂离子的迁移率，定义模拟盒子中一半锂离子从真空区域进入电极所需要的时间为τ。很显然扩散时间τ 与石墨及MoS2的结构有很密切的关系，利用这一变量可以量化石墨、MoS2及其复合材料G/MoS2的结构对锂离子扩散的影响。

2 结果与讨论

2.1 石墨、MoS2 层间距对锂离子扩散的影响

材料的层间结构（晶胞参数）往往可以通过离子掺杂等方法进行改良，但由于其他因素的影响，很难对其进行单一量化。本文运用NEMD模拟量化了石墨与MoS2的层间距（L）分别在0.34～0.50 nm 和0.61～1.00 nm 范围内锂离子的扩散情况。从图2（a）中可以看出，随着层间距的增大，锂离子的扩散时间先减小后增大，当石墨层间距在0.42 nm时，锂离子扩散时间最短（转化为传递扩散系数为4.32×10−2cm2/s），速率最快。图2（b）示出了锂离子的自扩散系数与石墨层间距的关系。从图中可以看出，当石墨的层间距约为0.46 nm 时，锂离子的自扩散系数（2.51×10−9cm2/s）最大，且随着层间距的增大，锂离子的自扩散系数增大到一定值后趋于平缓。图中曲线的变化揭示了电极材料的晶胞参数对锂离子扩散存在一定的影响。这与Xu 等[30]通过离子掺杂探究晶胞参数对其自扩散系数影响的结论相符（掺杂前后锂离子的自扩散系数分别为8.5×10−11cm2/s 和1.6×10−10cm2/s）。图2（a）和图2（b）差异的主要原因应该是由于扩散时间和自扩散系数是针对锂离子两个不同的运动状态计算的：扩散时间表征的是锂离子由真空区域进入电极的非平衡态过程，其主导因素为石墨中碳原子与锂离子之间的静电相互作用；而自扩散系数是锂离子处于平衡态时的扩散性质，其中熵效应是主导因素，所以当层间距较小时，随着层间距的增大，锂离子扩散的垂直空间增大，熵效应增大，自扩散系数随之增加；但当层间距增大到一定程度后，石墨层间C−C 的相互作用力减弱，再加上锂离子之间的排斥力，熵效应将不再随层间距的增大而增大，自扩散系数曲线趋于平缓。为了进一步解释这一现象，计算了不同层间距下石墨对锂离子的吸附能，结果如图3（a）所示。随着石墨层间距的增大，吸附能先增大后减小，其峰值和图2（a）中的峰值所对应的最佳层间距基本一致。这可能是由于在锂离子从真空区域向石墨电极迁移的非平衡态扩散过程中，吸附能在一定程度上代表着该层间距下锂离子迁移的动力。所以吸附能越高，锂离子在平衡态之前的迁移速率越大。从图2 中还可以看出，随着层间距的变化，扩散时间总体的浮动较小（变化零点几个皮秒），自扩散系数的浮动较大（变化2～3 个数量级），这可能是由于在本研究系统中，存在强电场作用，在锂离子迁移的非平衡态过程中，电场的驱动力充当了主要动力，削减了结构的影响，使扩散时间的浮动较小。

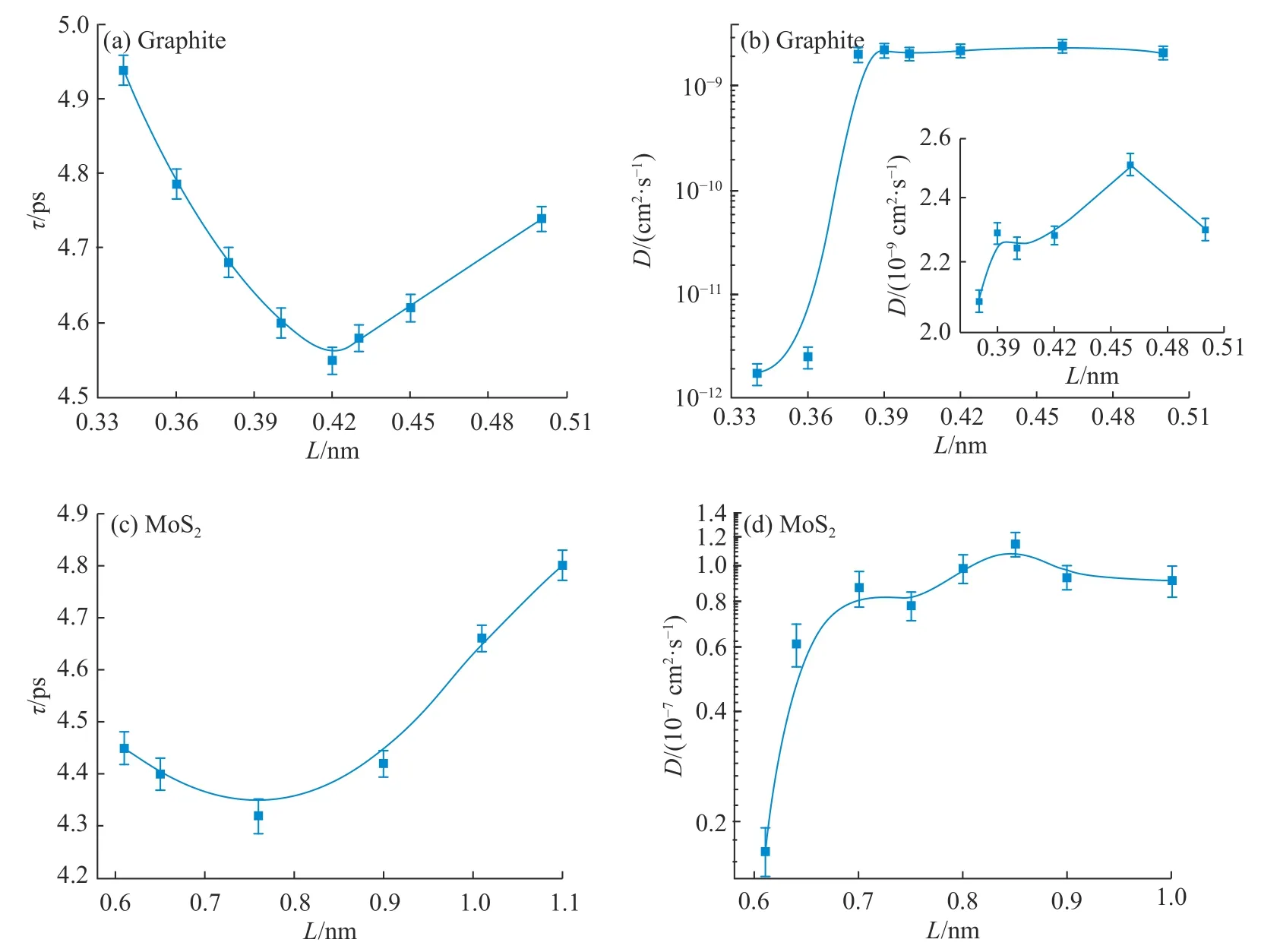
图2石墨和MoS2 的层间距对Li+扩散时间和自扩散系数的影响Fig.2Effect of the layer spacing of graphite and MoS2 on Li+ diffusion time and self-diffusion coefficient

通过比较图2 中扩散时间τ 和自扩散系数D 可以看出，体系的传递扩散系数和自扩散系数存在巨大的差别。皮秒级的传递时间所对应的传递扩散系数在10−2cm2/s 左右，这比对应的自扩散系数高出5～7个数量级，这种数量级上的巨大差别说明基于EMD的自扩散系数是无法正确描述LIBs 充放电过程的。其原因在于Einstein 方程主要考虑的是流体的自由扩散而忽略了外部势场的影响，仅能应用于近平衡态体系，而LIBs 的充放电过程中存在很强的外部电场，体系处于典型的非平衡态，与平衡态体系有较大区别，因而不能用Einstein 方程进行描述。

使用相同的方法计算了锂离子在MoS2不同层间距中的扩散性质。虽然MoS2的初始层间距为0.61 nm，但相邻两层S 原子之间的通道距离仅有0.289 nm，这使得大量的锂离子堆积在带负电荷的S 层间，阻碍了锂离子的进一步脱嵌和扩散。由于在锂离子从真空区域向MoS2电极迁移的非平衡态扩散过程中，吸附能在一定程度上代表着该层间距下锂离子迁移的动力，所以吸附能越高，锂离子在到达平衡态之前的迁移速率越大。结合图2（c）和图3（b），可以看出随着层间距的增大，锂离子的扩散速率先增大后减小，并在MoS2的层间距为0.75 nm 时扩散时间最短（转化为传递扩散系数为4.86×10−2cm2/s），扩散速率达到最佳。但从图2（d）中可以得出，当MoS2层间距为0.85 nm 时，锂离子的自扩散系数（1.15×10−7cm2/s）最大。扩散时间和扩散系数对应的最佳层间距及数值的差异再次强调了基于EMD 的自扩散系数无法正确描述LIBs 的充放电过程。

图3石墨和MoS2 的层间距对Li+吸附能的影响Fig.3Effect of the layer spacing of graphite and MoS2 on Li+ adsorption energy

2.2 石墨、MoS2 边缘基团对锂离子扩散的影响

作为一种界面传递，材料的表面状态尤其是边缘处的原子结构可能对整体传递过程起到显著影响。考虑体系的可操作性，探究了4 种石墨边缘不饱和碳上连接的常见基团，分别为C−H、C＝ O、C−F和C−OH，即可认为石墨边缘被一层氢、氧、氟、羟基原子包覆。从图4（a）中可以看出，石墨直线形边缘不饱和碳上连接的不同基团对锂离子扩散的影响存在差异，其中C−OH 的促进效果最为明显，之后依次为C−F>C＝ O>C−H。这一现象可能是由于边缘不饱和碳上连接的基团改变了材料边缘的电荷分布，从而影响了电极材料与锂离子之间的静电相互作用。分析基团中的电子结构可以看出，C−OH 中氧含有孤对电子，C−F 中氟的吸电子能力很强，所以相对于C−H 和C＝ O，前两者对锂离子有更强的吸引力。但由于氟原子与碳原子之间形成了稳定的化学键，而羟基上的氢可以被锂离子取代，所以C−OH 对锂离子的吸引力要比C−F 对锂离子的吸引力更大。

在实际电池的充放电过程中电流不同，其同时脱嵌的锂离子数也不同。为了使模拟数据更接近真实，探究了电池比容量（Q）不同时不同边缘基团对锂离子扩散时间的影响，结果如图4（b）所示。从图中可以得出，随着比容量的增大，扩散时间明显降低，这一结果再次验证了在强电场作用下电场驱动力的主导性。但边缘为C−F 和C−OH基团时，当比容量增大到一定程度后，τ 值趋于平缓甚至有回升的趋势，这可能是由于石墨的层间距较小，边缘不饱和碳连接−F 和−OH 官能团时，给锂离子的扩散造成了一定的空间位阻效应。且由于−F和−OH 的电负性较大，在锂离子迁移过程中有许多离子吸附在石墨的边缘，增大了静电屏蔽效应，影响了锂离子的进一步扩散。

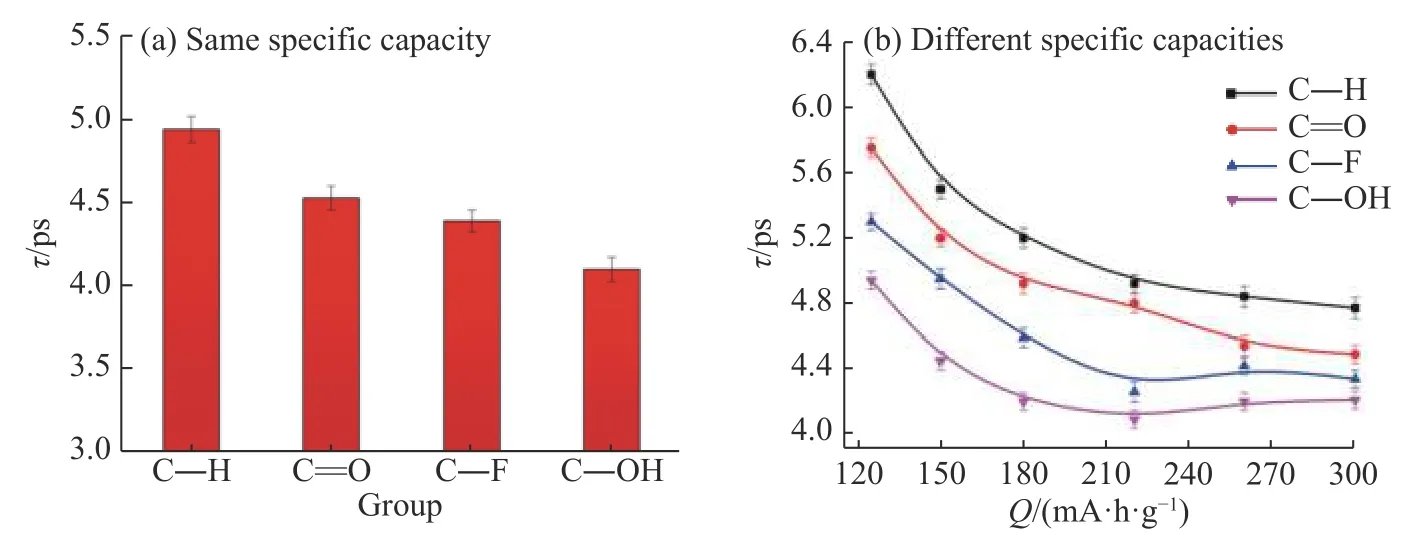
图4石墨边缘基团对Li+扩散时间的影响（L=0.34 nm）Fig.4Effect of graphite edge groups on Li+ diffusion time (L=0.34 nm)

除了边缘位功能团，材料表面的几何形貌亦可能对扩散过程产生影响[26-27]。对此，构建了具有锯齿形界面的石墨电极并考察其对扩散速率的影响，结果如图5 所示。从图中可以看出，对于锯齿形界面的石墨电极，4 种基团对锂离子扩散的促进效果和直线形界面的石墨电极一致，但锂离子的扩散时间整体略微缩短。分析其原因可能是由于锯齿形边缘相对于直线形边缘增大了与离子的碰撞概率，尤其是对于具有一定倾斜角度迁移的锂离子，更易通过碰撞嵌入电极。另外，锯齿形边缘增大了电极材料边缘的表面积，这在一定程度上也相应增强了边缘的电荷效应。

进一步讨论了当MoS2边缘为钼原子和硫原子时，锂离子的扩散性质。图6 所示为扩散达到平衡态时锂离子在MoS2中的位置分布。从图中可以看出，当边缘为钼原子时，锂离子均匀地分布在MoS2层中；当边缘为硫原子时，有大量锂离子吸附在硫原子的边缘，结合前文分析，这主要是由边缘基团的电负性引起的。对比锂离子在两种结构中的扩散时间（当边缘为硫原子时，τ=4.39 ps；当边缘为钼原子时，τ=4.58 ps），得出锂离子在两种结构中的扩散速率相差并不大，原因可能是当锂离子吸附在硫原子周边时，与硫形成了稳定的化学键，充当了原结构中钼原子的角色，这在一定程度上阻碍了锂离子的迁移。

2.3 G/ MoS2 复合材料构型对锂离子扩散的影响

由于单一的MoS2在导电性上具有劣势，因此目前的主流方法是将MoS2和石墨/石墨烯混合形成G/MoS2复合材料然后加以应用。基于石墨和MoS2的初始层状结构，考虑了6 种G/MoS2复合材料的构型，其结构主要是基于石墨和单层MoS2的复合均匀度建立的。将复合材料的结构统称为m+n 型，其中m 为单元石墨的层数，n 为单元MoS2的层数，如图7所示。在复合材料结构中，石墨的层间距hC-C=0.34 nm，MoS2的层间距hMo-Mo=0.61 nm，石墨和MoS2之间的层间距hC-S=0.40 nm。针对每一种复合结构，计算了锂离子的扩散时间和自扩散系数。从图8（a）中可以看出，锂离子在1+1 型的复合结构中扩散时间最短，自扩散系数最大。这说明石墨和MoS2的复合均匀度越大越有利于锂离子的扩散。

图5石墨锯齿形边缘基团对Li+扩散时间的影响Fig.5Effect of graphite serrated edge groups on Li+ diffusion time

图6MoS2 边缘为Mo 或S 原子时Li+分布结构图Fig.6Structure diagram of Li+ distribution when MoS2 edge is Mo or S atom

图7G/MoS2 复合材料结构类型Fig.7Structure types of G/MoS2 composites

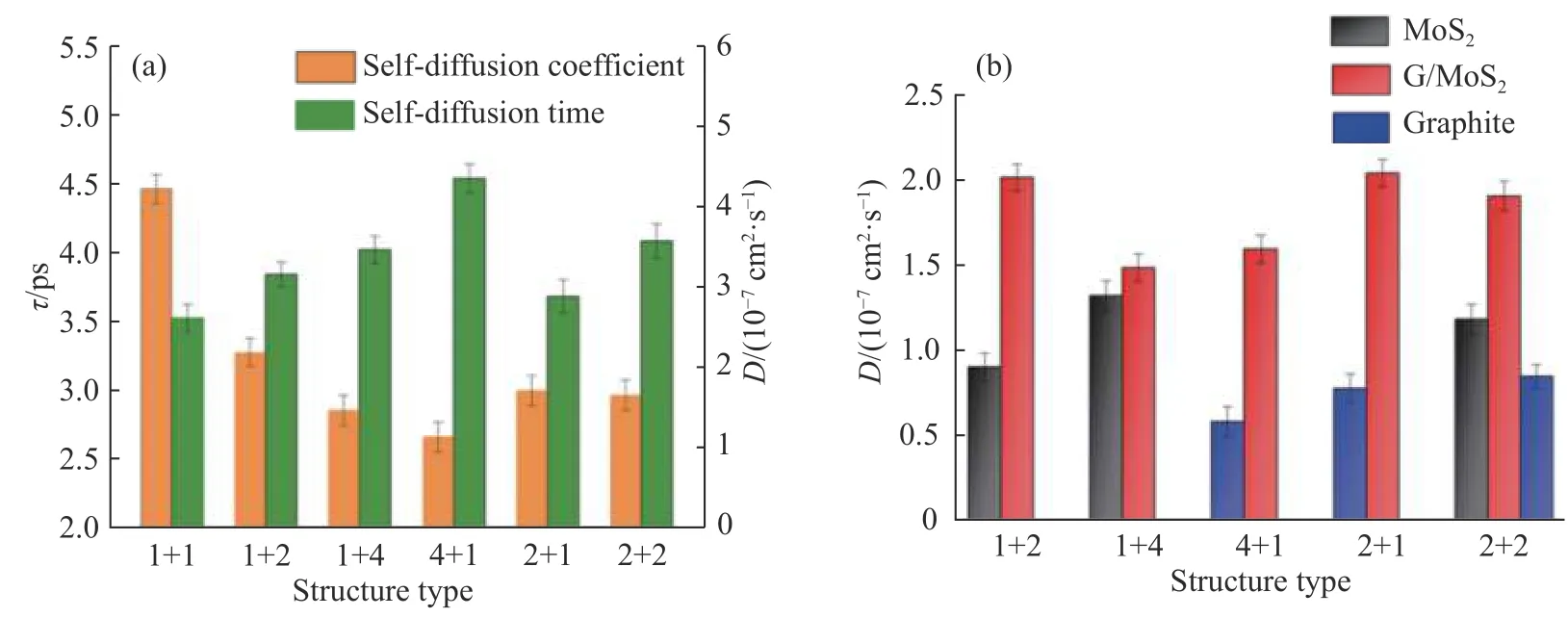
图8G/MoS2 复合材料结构对锂离子扩散的影响：（a）锂离子在复合材料中整体的扩散时间和自扩散系数；（b）锂离子在复合材料内部不同层间的自扩散系数Fig.8Effect of G/MoS2 composite material structures on lithium ion diffusion: (a) Overall diffusion time and self-diffusion coefficient of Li+in the composite materials; (b) Self-diffusion coefficient of Li+ between different layers in the composite materials

为了进一步详细探究复合材料内部结构的影响，分别计算了结构内部石墨层、MoS2层和G/MoS2复合层中锂离子的自扩散系数，结果见图8（b）。可以看出，无论哪一种结构，锂离子在G/MoS2复合层中的自扩散系数都最大。其原因可能是由于石墨中碳原子对锂离子的相互作用力相对于硫原子要弱，对锂离子扩散的限制作用减小，且Ebnonnasir等[31]曾指出石墨烯的加入会影响MoS2中Mo−S 键长，使得Mo−S 键长变短，石墨烯和MoS2之间层间距变大。所以锂离子在1+1 型复合材料中的扩散性能最佳。

3 结 论

运用非平衡态分子动力学模拟的方法并结合平衡态和量子力学研究了锂离子在石墨、MoS2和G/MoS2复合材料中的扩散性质，探讨了不同层间距、边缘结构的石墨和MoS2以及G/MoS2复合材料的构型。通过计算锂离子的迁移速率、扩散系数和吸附能，发现充放电过程中的锂离子传递不能用基于近平衡态假设的Einstein 方程进行描述。计算得到石墨和MoS2的最优层间距分别为0.42 nm 和0.75 nm。在不同的结构中，相对于扩散系数，扩散时间的变化较小。石墨边缘结构对锂离子迁移的促进顺序为：C−OH>C−F>C＝ O>C−H。G/MoS2复合材料的结构复合均匀度越高，越有利于锂离子的扩散。