非结构道路环境下的智能汽车质心侧偏角估计
2021-04-09王建锋李娜
王建锋 李娜


摘 要:车辆质心侧偏角是描述车辆侧向运动状态的重要参量之一,其估计的精度直接影响车辆的安全控制,传统的质心侧偏角估计方法不能满足非结构道路环境下的智能汽车质心侧偏角估计的要求。通过建立3 自由度智能汽车动力学模型,采用CarSim和MATLAB 构建智能汽车整车参数化模型;基于扩展kalman滤波(EKF)算法,设计非结构道路环境下的状态观测器对智能汽车质心侧偏角进行估计。在高、低附着系数路面双移线工况和蛇形工况下,对状态观测器的估计效果进行联合仿真验证。仿真结果表明:该方法能较精确地估计出非结构道路环境下智能汽车的质心侧偏角。
关键词:智能汽车;质心侧偏角;非结构道路;估计
中图分类号:U461 文献标识码:A
Sideslip Angle Estimation of Intelligent
Vehicle in Unstructured Road Environment
WANG Jian-feng1,2,LI Na1
(1.Shaanxi Road Traffic Intelligent Detection and Equipment Engineering Technology Research Centre, Changan
University, Xian,Shaanxi 710064,China;2.Shool of Automobile, Changan University,Xian,Shaanxi 710064,China)
Abstract:Sideslip angle of vehicle is one of the important parameters to describe the lateral motion state of vehicles, and the accuracy of its estimation directly affects the safety control of vehicles. The traditional sideslip angle estimation method can not meet the requirements of sideslip angle estimation of intelligent vehicles in unstructured road environment. Through the establishment of 3-dof vehicle dynamics model, CarSim and MATLAB were used to construct the parametric model of the whole intelligent vehicle. Based on the extended Kalman filter (EKF) algorithm, a state observer was designed to estimate sideslip angle of the intelligent vehicle. The estimation effect of the state observer was verified by the joint simulation under the double lane change test and double lane change test of road with high and low adhesion coefficient. The simulation results show that the proposed method can accurately estimate the sideslip angle of intelligent vehicle in unstructured road environment.
Key words:intelligent vehicle;sideslip angle;unstructured road;estimation
非結构化道路环境复杂,通常没有车道线和明显的道路边界。车辆在非结构化道路上行驶比在结构化道路上行驶更复杂。鉴于非结构道路环境的复杂性,研究非结构道路环境下的智能汽车主动控制具有重要的意义[1]。
质心侧偏角是汽车安全控制中的重要参数,实时、准确地获取汽车的质心侧偏角是实现车辆安全控制的重要保障,尤其在非结构道路环境下。汽车的质心侧偏角定义为汽车质心处的侧向速度与纵向速度的比值,无法直接测量。只能通过车载传感器测量汽车侧向加速度、横摆角速度、转向盘转角等参数采用数据融合的方法进行估计。
目前,质心侧偏角估计的方法主要有基于数值积分的估计方法、基于动力学模型估计方法和基于机器学习的估计方法。数值积分的估计方法主要是利用横摆角速率和侧向加速度等通过数值积分估算出车辆的侧向速度,计算汽车的质心侧偏角,该方法受传感器信号噪声的影响,积分结果存在累积误差[2-4]。基于动力学模型估计方法是通过建立精确的动力学模型,利用可测量的模型输入参数估计质心侧偏角,该方法估计精度直接依赖于动力学模型,很难在非线性段进行准确估计[5-6]。基于机器学习的估计方法是利用机器学习的方法对可测变量和已知的质心侧偏角的样本数据进行训练,建立起输出参数和质心侧偏角之间的映射关系,其估计精度依赖于样本的质量和数量[7-8]。
综合基于数值积分的估计方法和基于动力学模型估计方法的优点,在汽车的线性区采用动力学模型方法,在汽车的非线性区采用数值积分的方法,基于汽车动力学模型及kalman滤波算法设计智能汽车质心侧偏角状态观测器。
1 智能汽车3自由度非线性模型
为了设计有效的非结构道路环境下的智能汽车质心侧偏角估计器,首先建立可靠的智能汽车动力学模型。兼顾侧偏角估计的精度和估计算法实时性求解的要求,考虑车辆的侧向运动、横摆运动及侧倾运动,建立如式(1)所示的3自由度车辆动力学模型[9-10]。
将非线性模型转换为线性模型,虽然能够较好地解决kalman滤波算法在处理非线性系统时的发散问题,但是并不是在任何時候都能有较高的估计精度。主要原因是卡尔曼滤波器的输出由模型预测和测量反馈校正两部分组成,滤波器的输出精度由测量模型精度和测量反馈校正综合决定。当测量噪声较大时,估计精度主要依赖于模型预测精度,当系统噪声较大时,估计精度主要依赖于测量反馈校正。因此综合基于数值积分估计方法和动力学模型估计方法的优点,在汽车的线性区采用动力学模型方法,在汽车的非线性区采用数值积分方法,基于汽车动力学模型及kalman滤波算法设计智能汽车质心侧偏角状态观测器。
2.2 智能汽车质心侧偏角状态观测器设计
基于所建立的智能汽车动力学模型和基kalman 滤波器的质心侧偏角估计方法,设计非结构道路环境下的智能汽车质心侧偏角状态观测器。观测器的输入变量为U(t)=(δ),输出变量为Y(t)=ωr φ·T,状态变量为X(t)=β ωr φ φ·T。将所建立的动力学模型转化为状态方程的形式为:
利用所建立的智能汽车质心侧偏角状态观测器就可以估计出智能汽车在不同工况下的质心侧偏角。
3 智能汽车质心侧偏角估计仿真
为了验证提出的非结构道路环境下的智能汽车质心侧偏角估计效果,参照ISO标准进行双移线工况和蛇形工况仿真实验,实验用智能汽车的主要仿真参数如表2所示。
3.1 高附着系数路面双移线仿真
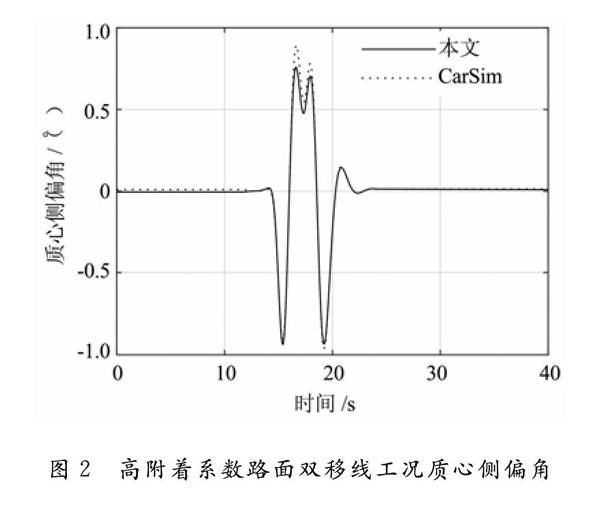
利用以上参数进行高附着系数路面下的双移线仿真试验,设定智能汽车的最高速度为100 km/h,路面附着系数为0.8 ,仿真时间为40 s,仿真结果如图1-图2所示。
从图1 可以看出,在车速为100 km/h,路面附着系数为0.8 的双移线工况下,侧向加速度小于0.4 g,可见轮胎处于线性区域。从图2 可以看出,高附着系数双移线工况下本文方法和CarSim 仿真结果很接近,最大峰值误差为4.7 %。
3.2 低附着系数路面双移线仿真
利用以上参数进行低附着系数路面下的双移线仿真试验,设定汽车的最高速度为80 km/h,路面附着系数为0.4 ,仿真时间为40 s,仿真结果如图3-图4所示。
从图3 可以看出,在车速为80 km/h,路面附着系数为0.4 的双移线工况下,侧向加速度曲线在第一个波谷和第二个波峰出超过了0.4 g,在该两处轮胎处于非线性区域。从图4 可以看出,低附着系数双移线工况下本文方法和CarSim 仿真结果也较接近,但在轮胎非线性区误差相对较大,最大峰值误差为5.3 %。
3.3 高附着系数路面蛇形仿真
利用以上参数进行高附着系数路面下的蛇形仿真试验,设定汽车的最高速度为60 km/h,路面附着系数为0.8 ,仿真时间为40 s,仿真结果如图5-图6所示。
从图5 可以看出,在车速为60 km/h,路面附着系数为0.8 的蛇形工况下,在侧向加速度曲线的第1、2、3 个波谷处,第2、3、4 个波峰处都超过了0.4 g,可见轮胎处于了非线性区域。从图6 可以看出,高附着系数双移线工况下本文方法和CarSim 仿真结果非常接近,主要误差出现在轮胎进行非线性区段,本文方法与CarSim 的质心侧偏角的最大峰值误差为3.1 %。
3.4 低附着系数路面蛇形仿真
利用以上参数进行低附着系数路面下的蛇形仿真试验,设定汽车的最高速度为40 km/h,路面附着系数为0.4 ,仿真时间为40 s,仿真结果如图7-图8所示。
从图7 可以看出,在车速为40 km/h,路面附着系数为0.4 的蛇形工况下,侧向加速度小于0.4 g,可见轮胎处于了线性区域。从图8 可以看出,低附着系数蛇形工况下本文方法和CarSim 仿真结果非常接近,本文方法与CarSim 的质心侧偏角的最大峰值误差为1.9 %。
4 结 论
针对非结构道路环境下的智能汽车质心侧偏角估计问题,基于智能汽车动力学模型及Kalman滤波算法,设计了智能汽车质心侧偏角状态观测器。利用高、低附着系数路面下双移线工况和高、低附着系数路面下蛇形工况对智能汽车质心侧偏角状态观测器的估计效果与carsim仿真结果进行
对比,仿真结果表明所设计的智能汽车质心侧偏角状态观测器输出的估计值与CarSim 整车参数化模型输出值虽在曲线波峰和波谷处存在一定的偏差,但其趋势基本相同,且估计精度较高,达到了预期估计目标,能够满足非结构道路环境下的智能汽车控制的要求。
参考文献
[1] 赵俊梅,张利平.智能车辆中非结构化道路检测技术的研究[J].车辆与动力技术,2010,(4):10-13+24.
[2] PIYABONGKARN D,RAJAMANI R,GROGG J A,et al. Development and experimental evaluation of a slip angle estimator for vehicle stability control[J]. IEEE Transactions on Control Systems Technology, 2009,17(1):78-88.
[3] 张晨晨,夏群生,何乐.质心侧偏角对车辆稳定性影响的研究[J].汽车工程,2011,(4):277-282.
[4] CHEN B C,HSIEH F C. Sideslip angle estimation using extended Kalman filter[J]. Vehicle System Dynamics, 2008, 46(sup):353-364.
[5] STEPHANT J,CHARARA A,MEIZEL D. Virtual sensor: application to vehicle sideslip angle and transversal forces[J]. IEEE Transactions on Industrial Electronics, 2004, 51(2):278-289.
[6] 皮大偉,张丙军,钟国华. 汽车质心侧偏角观测器试验验证[J].河北科技大学学报,2013,(4):113-118.
[7] CHELI F,SABBIONI E,PESCE M, et al. A methodology for vehicle sideslip angle identification: comparison with experimental data [J]. Vehicle System Dynamics, 2007,45(6):549-563.
[8] HE Jun-jie, CROLLA D A,LEVESLEY M C, et al. Coordination of active steering, driveline, and braking for integrated vehicle dynamics control[J]. Journal of Automobile Engineering, 2006, 220(1):1401-1421.
[9] 林棻,赵又群,姜宏. 基于Simulink 的四轮转向汽车神经网络控制策略仿真[J]. 江苏大学学报(自然科学版),2008,29(5):390-393.
[10]姜宏.基于Matlab/Simulink 和神经网络的四轮转向车辆控制研究[D].南京:南京航空航天大学,2007.
[11]方春杰.纯电动汽车质心侧偏角估计及仿真分析[J].汽车工程师,2017,(11):34-38.
[12]刘飞,熊璐,邬肖鹏,等.车辆质心侧偏角估计算法设计与对比分析[J]. 同济大学学报(自然科学版),2015,43(3):448-455.
