中小跨径刚柔组合式钢桥面铺装力学响应研究

张可强，曹 健,*，吴 钊

(1. 苏交科集团股份有限公司，南京 211112；2. 新型道路材料国家工程实验室，南京 211112)

钢桥面铺装是直接铺设正交异性钢桥面板，铺装层可提供行车舒适性与安全性，并保护钢桥面的结构层[1]。经过数十年研究与应用，已形成以双层EA(双层环氧沥青)、GA(浇注式沥青)及双层SMA(双层改性沥青SMA)为代表的几大主流铺装方案[2-3]。

受限于工程规模与建设投资等因素，已有大跨径桥梁钢桥面铺装方案并不适用于中小跨径桥梁。基于水泥混凝土桥梁桥面铺装在各地的成功应用，我国已建及在建的中小跨径钢结构桥梁的桥面铺装往往采用刚柔组合式铺装结构，即利用水泥混凝土层将光滑的钢箱梁面板转化为近似水泥混凝土箱梁的粗糙界面。然而，相较于常规水泥混凝土桥梁，钢结构桥梁铺装层受力更为复杂，且铺装层自身刚度、厚度等材料性能的变化都将导致铺装层受力状态的变化[4-6]，加之国内部分地区高温重载及雨热同季的使用环境，上述铺装方案在实际应用过程中病害频发。

因此，依托南京至马鞍山国家高速公路油坊桥互通枢纽G匝道(跨径组合为45 m+45 m+29.2 m，刚柔组合式铺装结构如图1所示)，开展刚性铺装层弹性模量、不同车型荷载作用形式、结构层相对厚度等因素对铺装层力学响应的影响规律研究。这对于中小跨径刚柔组合式钢桥面铺装结构设计与材料指标优化，提高我国中小跨径钢结构桥梁桥面铺装水平，推动中小跨径钢结构桥梁建设具有重要意义。

图1 刚柔组合式铺装结构

1 有限元模型的建立

1.1 模型基本参数

本文运用大型通用有限元分析软件ABAQUS，建立了三跨结构局部有限元模型。其中，钢桥面板、T形加劲肋、横隔板采用SHELL63空间壳单元模拟，钢桥面铺装层采用SOLID45三维节点的等参实体单元模拟。局部模型总长约6 m(中线)，模型尺寸参数如表1所示；局部模型如图2所示。

表1 模型尺寸参数 (mm)

图2 局部模型

1.2 荷载及约束

本研究所用荷载及约束条件为：荷载采用矩形均布荷载，荷载作用范围为20 mm×18 mm；将两端横隔板进行固结，并限制端部横隔板的位移。

2 极端荷位确定

2.1 荷位选取

本项目为匝道桥，横向超高较多(横坡达到5%)，导致桥梁内外侧受力不同，因此，在进行横向荷位选取时应充分考虑桥梁内外侧的差异性，其中，横桥向荷位如图3所示，纵桥向荷位如图4所示。

图3 横桥向荷位

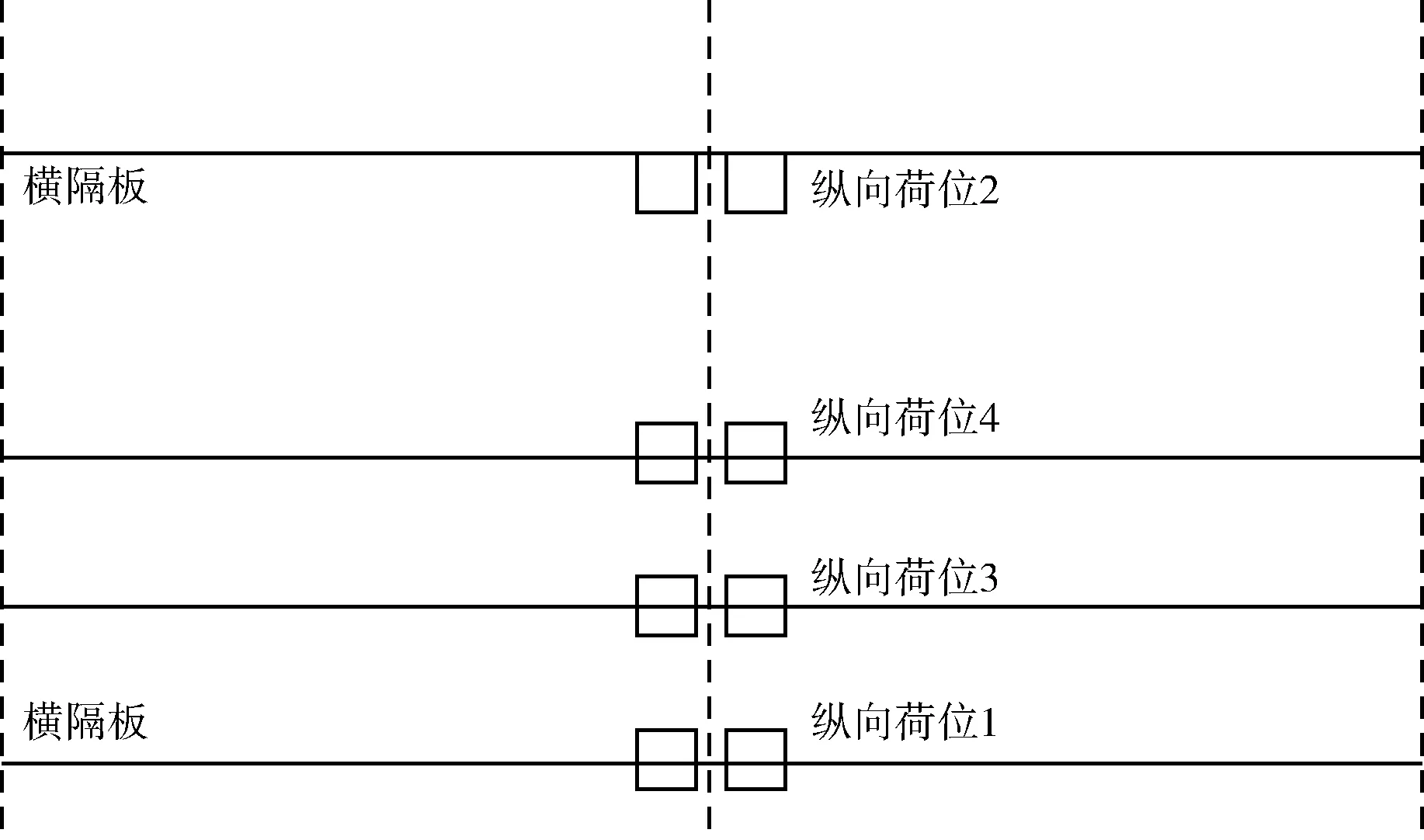
图4 纵桥向荷位

2.2 极端荷位的确定

所建局部模型在上述7个横向荷位与4个纵向荷位下的力学响应数据构成不同荷位下铺装层的力学响应结果，如图5所示。

(a) 沥青层最大横向拉应力

基于上述力学响应结果，综合考虑各指标的力学响应与边界约束的影响，确定各指标对应的极端荷位，如表2所示。

表2 各指标对应的极端荷位

3 影响因素分析

研究表明，桥梁主体刚度、铺装层厚度及刚度、车辆荷载布置形式等因素对钢桥面铺装层力学响应结果具有不同程度的影响。其中，桥梁主体刚度主要根据《公路钢结构桥梁设计规范》(JTG D64—2015)进行设计，桥梁主体刚度满足结构要求且对大纵坡小半径桥面铺装影响不大，故本研究中不对该因素进行模拟分析；铺装下层C50钢纤维水泥混凝土层弹性模量一般为35～40 GPa，且随着钢纤维掺量及配合比参数等因素变化，其变化幅度可达5%～10%，该变化值已超过铺装上层沥青混合料的最大弹性模量，而铺装上层沥青混合料弹性模量变化不大，因此本研究中假定其为定值。

3.1 刚性铺装层弹性模量

同一强度等级的水泥混凝土，由于砂率、水胶比、粗集料粒径、纤维种类及掺量的不同，其弹性模量也不同[7-8]。铺装层与桥面板间的相对刚度将随着铺装层弹性模量的不同而发生变化，进而导致铺装层的应力分布发生改变[9-10]。为研究刚性铺装层弹性模量变化对铺装结构力学响应的影响规律，本文分别设置刚性铺装层弹性模量为35 GPa、40 GPa、45 GPa、50 GPa、55 GPa和60 GPa，不同弹性模量下的计算结果如表3所示。

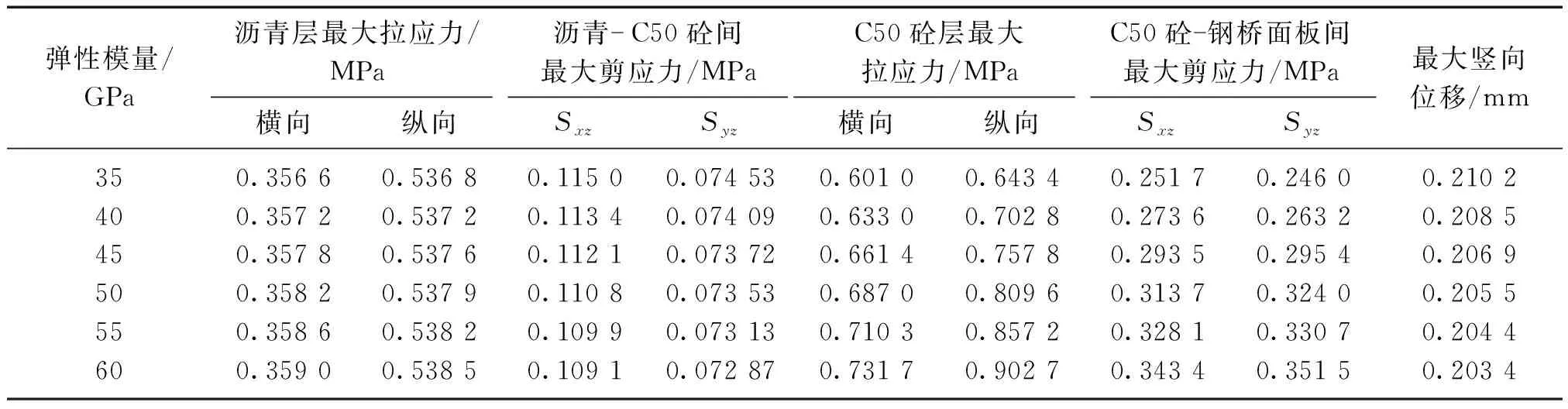
表3 不同弹性模量下的计算结果

由表3可知：①刚性铺装层弹性模量的改变对柔性铺装层、层间黏结层及整体竖向位移影响较小，当刚性铺装层弹性模量由35 GPa增加至60 GPa 时，柔性铺装层拉应力变化均不超过1%，上下铺装层间剪应力变化幅度最大仅为5.1%，铺装层整体最大竖向位移变化幅度为3.2%，远小于模量自身变化幅度；②刚性铺装层弹性模量变化对其自身及其与钢桥面板间受力影响较其他指标显著，其中，刚性铺装层最大纵向拉应力变化幅度为21.7%、刚性铺装层最大横向拉应力变化幅度为40.3%，铺装层与钢桥面板间纵向剪应力变化幅度为36.4%、铺装层与钢桥面板间最大横向剪应力变化幅度为42.9%。

3.2 荷载布置形式

在常规力学计算时，通常采用半轴双轮的标准荷载，但根据《公路桥涵设计通用规范》[11](JTG D60—2015)可知，车辆双后轴间距为1.4 m，由于双后轴车辆后两轴距离较小，互有影响，为掌握双后轴共同作用下铺装层受力变化情况，保持原定最不利荷位，距原荷位1.4 m处增设一组相同荷载，不同轴数作用下的计算结果如表4所示。

表4 不同轴数作用下的计算结果

由表4可知，与单半轴荷载相比，双半轴荷载作用下，上下铺装层间Syz方向最大剪应力变化较为明显，双半轴作用下该剪应力增幅达到45.25%；刚性铺装层最大纵向拉应力次之，增幅为14.87%，其余力学指标变化幅度相对较小，均未超过10%。且在两种荷载作用形式下，上下铺装层间Syz方向剪应力均小于Sxz方向剪应力。因此，可以认为两种作用形式对铺装层整体力学响应影响较小。

双半轴双轮荷载作用下的Mises应力云图如图6所示，结合表4可知，双后轴间主要影响区域间隔较远，两者相互影响较小。同时，考虑到网格划分不同对计算结果带来的影响，为简化计算，在进行力学分析时可忽略双后轴间的相互影响，采用单半轴荷载进行计算。

图6 双半轴双轮荷载作用下的Mises应力云图

3.3 结构厚度

各结构层厚度与铺装层总厚度对铺装层与钢桥面板间的相对刚度也有影响[12]，为不改变铺装体系整体标高及不造成铺装层恒载的大幅改变，保持铺装体系总厚度不变，调整上下铺装层厚度，不同结构组合形式具体参数如表5所示，不同结构力学响应的计算结果如表6所示。

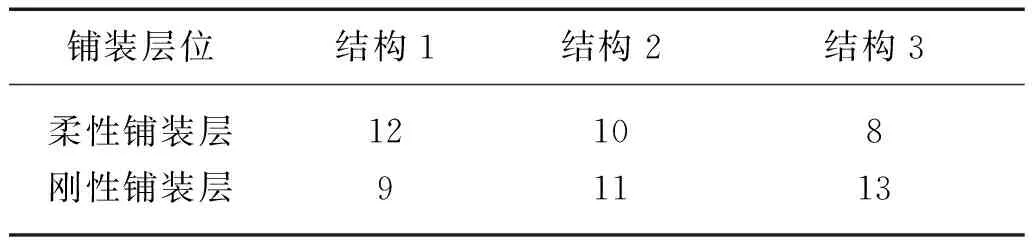
表5 不同结构组合形式具体参数 (cm)

由表6的计算结果可知，柔性铺装层最大拉应力及上下铺装层间最大剪应力值与刚性铺装层厚度间呈正相关，而刚性铺装层自身受力有所改善。同时，铺装层整体最大竖向位移减小。综合考虑不同组合形式下各结构层的力学响应情况、桥梁恒载及工程造价等因素，建议采用“10 cm柔性铺装上层+11 cm刚性铺装下层”的结构组合形式。

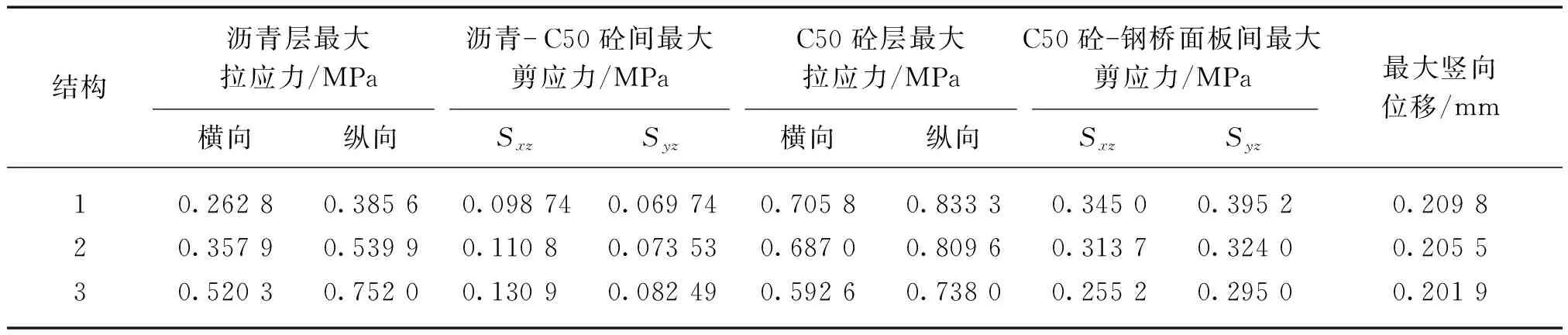
表6 不同结构力学响应的计算结果

3.4 钢筋网片

不同于双层EA、GA+SMA/AC及ERS组合式等铺装方案，刚柔组合式铺装方案中，基于水泥混凝土抗压不抗折的特性，为提高刚性铺装层的抗变形能力，往往在水泥混凝土层内布设钢筋网片。为研究钢筋网对铺装层受力的影响，在模型中增设Φ10@150的钢筋网，在最不利荷位下施加荷载，增设钢筋网计算结果如表7所示。

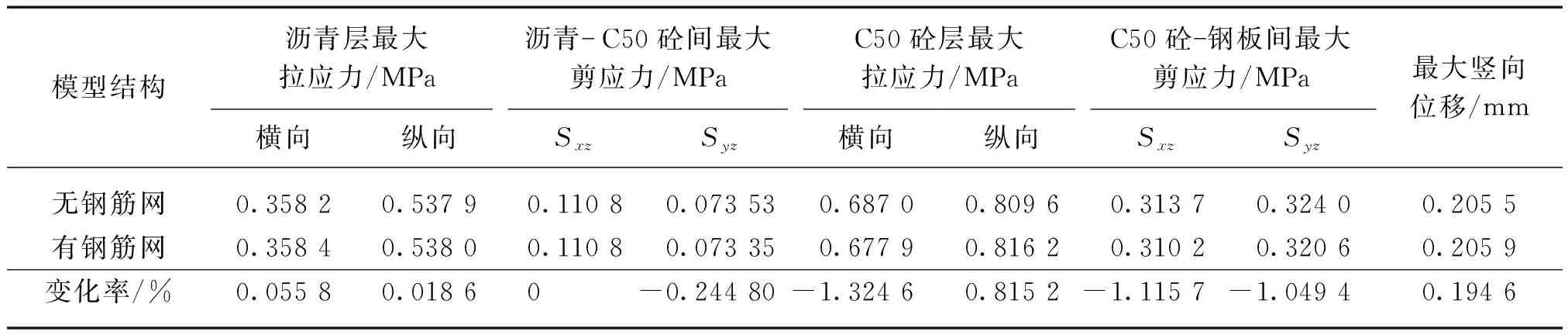
表7 增设钢筋网计算结果

由表7可知，刚性铺装层增设钢筋网片后，各力学指标数值虽有所变化，但变化幅度均较小，其中刚性铺装层横向拉应力变化幅度最大，但仅为1.3%。因此，可认为增设钢筋网的主要作用是提高刚性铺装层的抗变形能力，对铺装层力学响应影响较小。

4 结论

(1) 刚性铺装层弹性模量变化对柔性铺装层、层间黏结层及铺装层整体竖向位移影响较小，对刚性铺装层及铺装层与钢桥面板间受力影响相对较大，其中，刚性铺装层最大纵向拉应力变化幅度为21.7%、刚性铺装层最大横向拉应力变化幅度为40.3%，铺装层与钢桥面板间最大纵向剪应力变化幅度为36.4%、铺装层与钢桥面板间最大横向剪应力变化幅度为42.9%。

(2) 双后轴间主要影响区域间隔较远，两者相互影响较小，为简化计算，在进行力学分析时可忽略双后轴间的相互影响，采用单半轴荷载进行计算。

(3) 随着刚性铺装层厚度的增加，柔性铺装层最大拉应力及铺装层间最大剪应力值增大，而刚性铺装层力学响应数值及铺装层竖向位移减小，铺装层厚度并非越大受力越有利。

(4) 刚性铺装层增设钢筋网片对铺装层力学响应影响较小，其中以刚性铺装层横向拉应力变动最大，但也仅为1.3%。